ABZ¨AHLPROBLEME BEI B¨AUMEN Es sei B die Familie der

ABZÄHLPROBLEME BEI BÄUMEN
HELMUT PRODINGER (WIEN)
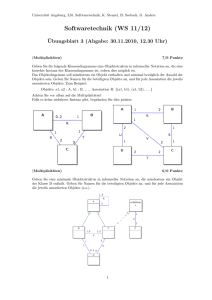
Es sei B die Familie der binären Bäume. B kann durch eine formale Gleichung beschrieben
werden:
k
+
B =
B
B
Dies besagt, daß ein binärer Baum entweder ein Blatt (externer Knoten) ist, oder eine Wurzel
zusammen mit einem linken und einem rechten Teilbaum, welche selbst binäre Bäume sind.
Diese formale Gleichung kann übersetzt werden in eine Gleichung für die erzeugende Funktion
B(z):
B(z) = 1 + zB 2 (z);
!
√
X
1 − 1 − 4z
1
2n n
B(z) =
=
z .
2z
n
+
1
n
n≥0
Binäre Bäume können verwendet werden, um arithmetische Ausdrücke darzustellen:
×
←→
+
3
7
3 × (7 + 4)
4
Die Auswertung kann mit Hilfe von Registern erfolgen; diese werden verwendet, um
Zwischenergebnisse zu speichern.
Die Registerfunktion Reg(t) ist definiert als die minimale Anzahl von Registern zur Auswertung des Baumes t unter Verwendung der optimalen Strategie.
1
2
ABZÄHLPROBLEME BEI BÄUMEN
Es gilt:
Reg() = 0
Reg
g
t1
(
=
1 + Reg(t1 )
falls Reg(t1 ) = Reg(t2 )
max{Reg(t1 ), Reg(t2 )}
t2
Es sei Rp (Sp ) die Familie der Bäume mit Registerfunktion = p (≥ p); Rp (z) und Sp (z)
seien die entsprechenden erzeugenden Funktionen. Man sieht unmittelbar:
Rp
=
+
Rp−1
+
P
Rp−1
j<p
Rp
Rj
=
Sp−1
+
B \ S p−1
X
Rj ,
Sp
R0 = 1 ,
j<p
2
Sp = zSp−1
+ 2zSp (B − Sp−1 ),
Sp =
Wir setzen ε :=
√
S0 = B ;
2
zSp−1
.
1 − 2zB + 2zSp−1
1 − 4z = 1 − 2zB :
ε 1
1
1
+2
=
.
2
Sp
z Sp−1
Sp−1
Wir multiplizieren mit ε/z und substituieren Up := ε/zSp :
2
Up = Up−1
+ 2Up−1 ⇒ Up + 1 = (Up−1 + 1)2 ⇒
ε
p
Up = −1 + (U0 + 1)2 ; U0 =
⇒
zB
1
ε
Sp = ·
p .
z −1 + 1+ε 2
1−ε
Rj
g
Daher gilt:
2
Rp = zRp−1
+ 2zRp
P
j<p
+
Sp−1
Rp
g
g
Sp
g
g
g
Sp B \ S p−1
sonst
ABZÄHLPROBLEME BEI BÄUMEN
3
Es ist günstig, z = u/(1 + u)2 zu setzen:
p
Sp =
u2
1 − u2
·
u
1 − u 2p
p
1 − u2
u2
·
.
u
1 − u2p+1
Sei nun Mn die mittlere Registerfunktion eines binären Baumes mit n Knoten. Es gilt:
Rp = Sp − Sp+1 =
Mn =
P
p · [z n ]Rp (z)
[z n ] p≥1 Sp (z)
=
.
[z n ]B(z)
[z n ]B(z)
P
p≥0
Wir studieren den Zähler:
p
1 − u2 X u2
E(z) =
Sp (z) =
u p≥1 1 − u2p
p≥1
X
=
1 − u 2 X 2p λ
u
u p≥1
λ≥1
=
mit v2 (k) =
P
k=2p λ,
p,λ≥1
1−
u
u2
X
v2 (k)uk
k≥1
1 . (Beachte v2 (2n) = 1 + v2 (n), v2 (2n + 1) = 0.)
Um den Koeffizienten von z n in E(z) zu finden, bedienen wir uns einer analytischen
Methode. Das Verhalten der Koeffizienten wird nämlich weitgehend beschrieben durch das
Verhalten der erzeugenden Funktion in der Nähe der Singularitäten am Konvergenzkreis. Es
liegt eine Singularität bei u = 1 vor.
Mit Hilfe der Mellin–Transformation findet man für t → 0:
X
v2 (k)e−tk ∼
X
Res
s
k≥1
Γ(s)ζ(s) −s
t
2s − 1
und insgesamt (z → 1/4)
3
γ
E(z) ∼ 2ε log2 ε + 2
− log2 2π +
2
log 2
Beachtet man noch, daß
+4
X
ε1−χk mit χk =
k6=0
2kπi
log 2
4n
[z n ]B(z) ∼ √ n−3/2
π
ist, folgt nun
Mn ∼ log4 n −
χ /2
1
γ
1
1 X
χk −
−
+ log2 2π +
ζ(χk )Γ
(χk − 1)n k .
2 2 log 2 log 2
log 2 k6=0
2
Es gilt nχk /2 = e2kπi·log4 n , und somit Mn ∼ log4 n + D(log4 n).
Hier ist D(x) eine periodische Funktion mit Periode 1.
4
ABZÄHLPROBLEME BEI BÄUMEN
Die Fourierreihenentwicklung D(x) = k dk e2kπix ist:
1
γ
1
−
+ log2 2π,
d0 = − −
2 2 log 2 log 2
1
χk dk =
ζ(χk )Γ
(χk − 1), k 6= 0,
log 2
2
P
χk =
2kπi
.
log 2
Man kann auch Motzkinbäume betrachten:
e
M
e
+
+
=
M
M M
M kann aus B durch Substitution gewonnen werden:
-
g
∗
-
g
∗
g
g
Daher:
1
z
M (z) =
B
.
1−z
(1 − z)2
Die Registerfunktion von Bäumen aus M wird durch die folgende Erweiterung gewonnen:
e
Reg
t
Es gilt auch
z
1
=
Rp
usw.
1−z
(1 − z)2
Deshalb ist die mittlere Registerfunktion jetzt gegeben durch
Rp(M) (z)
1
[z n ] 1−z
E
1
[z n ] 1−z
B
z
(1−z)2
z
(1−z)2
.
Ähnlich wie vorher erhält man
∼ log4 n + D̄(log4 n).
= Reg(t)
ABZÄHLPROBLEME BEI BÄUMEN
5
g
g
+ c1 ·
F = c0 ·
+ c2 ·
F
F
F
Die Situation kann noch verallgemeinert werden durch Gewichte:
In einem binären Baum bezeichnen wir einen Knoten t als kritisch, falls die Registerfunktion des linken und rechten Unterbaumes gleich sind. Nach längerer Rechnung erhält man:
die mittlere Anzahl der kritischen Knoten eines binären Baumes mit n Knoten ist
[z n ]V (z)
,
[z n ]B(z)
wo
u(1 + u)
1 − u2 X
V (z) =
−2·
ω(k)uk ; ω(k) = i falls k = 2m (1 + 2i).
1−u
u k≥1
Durch ähnliche Methoden wie vorher erhält man:
“ungefähr n3 Knoten sind kritisch”
Man kann auch explizit errechnen, daß
n
[z ]V (z) =
!
X
2n
−2
ω(k)
n−1
k≥1
"
!
!
2n
2n
2n
−2
+
n+1−k
n−k
n−1−k
!#
.
Durch partielle Summation (zweimal durchzuführen) und Information über
X X
ω(k)
n<N k≤n
kann man das asymptotische Verhalten auch relativ “elementar” (dafür mühsam) errechnen.
Auf eine ungelöste Frage im Zusammenhang mit der Registerfunktion binärer Bäume soll
noch eingegangen werden: Die erzeugende Funktion der binären Bäume mit Registerfunktion
< p ist
F2p −1 (z)
B(z) − Sp (z) =
,
F2p (z)
mit
!
X n−1−j
Fn (z) =
(−z)j (Fibonaccipolynom).
j
j
Die linksseitige Höhe h eines binären Baumes ist definiert durch
h() = 0
h
e
t1 t2
=
max{1 + h(t1 ), h(t2 )}
6
ABZÄHLPROBLEME BEI BÄUMEN
Die erzeugende Funktion der Bäume mit h(t) < h ist
Fh (z)
Fh+1 (z)
Somit ist die Anzahl der binären Bäume mit n Knoten und Registerfunktion < p gleich der
Anzahl der binären Bäume mit n Knoten und linksseitiger Höhe < 2p − 1. Gesucht ist eine
geeignete Bijektion dieser Objekte.
1.
2.
3.
4.
5.
6.
7.
8.
Literatur
N.G.de Bruijn, D.E.Knuth, S.O.Rice: The average height of planted plane trees, in:
Graph Theory and Computing (R.C.Read, Ed.), 15-22, Academic Press, 1972.
P.Flajolet: Analyse d’algorithmes de manipulation d’arbres et de fichiers, Thèse ParisSud-Orsay, 1979.
P.Flajolet, A.Odlyzko: The average height of binary trees and other simple trees, JCSS
25(1982), 171-213.
P.Flajolet, H.Prodinger: The number of registers to evaluate unary-binary trees, SIAM
J. Computing 15(1986), 629-640.
P.Flajolet, J.C.Raoult, J.Vuillemin: The number of registers required for evaluating
arithmetical expressions, TCS 9(1979), 99-125.
R.Kemp: The average number of registers to evaluate a binary tree optimally, Acta
Inf. 11(1979), 313-372.
H.Prodinger: Some recent results on the register function of a binary tree, Annals of
Discrete Math. 33(1987), 241-260.
H.Prodinger, R.F.Tichy: Über ein zahlentheoretisches Problem aus der Informatik,
Sitzungsberichte der Österreichischen Akademie der Wissenschaften, Abt. II, 192(1983),
385-396.