iii.buch pyramiden - Wehrle-Formeln für Dreiecke, Vierecke

III.BUCH PYRAMIDEN
5. Die RAUMWINKELSUMME
1
Die Raumwinkelsumme einer Dreieckspyramide ist nicht π
Der
Raumwinkel
ist
die
natürliche
Verallgemeinerung
eines
zweidimensionalen Winkels auf höhere Dimensionen. Während in der
Ebene
ein
ausgehenden
Winkel
durch
Strahlen
zwei
oder
von
einem
Halbgeraden
Punkt
(dem
eingegrenzt
ist,
Scheitel)
wird
im
Dreidimensionalen ein Raumwinkel (sphärischer- oder Festkörperwinkel)
durch drei sich in einem Punkt schneidenden Halbebenen bzw. durch
den rotationsymmterischen Kegelöffnungswinkel definiert. Hat man im
Zweidimensionalen die aus dem Einheitskreis ausgeschnittene Bogenlänge
als Winkelmaß verwendet1, ist nun analog das von der Einheitskugel
ausgeschnittene
Kugelsegment
ein
Maß
für
den
sphärischen
Raumwinkel.
Allerdings gibt es nun eine unendliche Vielfalt an räumlichen
Winkeln derselben Größe, da es ja ebenso viele Möglichkeiten gibt,
gleichgroße Flächen auf der Einheitskugel zu erzeugen. Darunter ist
im
symmetrischsten
aller
Fälle
ein
rotationssymmetrischer,
kegelförmiger Winkel, dessen Schnitte mit der Einheitskugel eine
Kreisfläche bildet. Ist beispielsweise der Öffnungswinkel φ eines Kegels
120° (Drehwinkel 60°), dann ist der Raumwinkel gerade π:
Ω = 4π sin² (¼φ).
War die Einheit zuvor Radiant (rad), so nennt man sie nun Steradiant
(sr2). Schlossen zuvor die Koordinatenachsen einen Winkel von ½π ein,
nämlich den vierten Teil des Umfangs 2π des Vollkreises mit Radius 1, so
schließen nun die die Koordinatenebenen wiederum einen Winkel von ½π
1
Beim sog. Bogenmaß gegenüber dem willkürlich in 360 Teile eingeteilten Gradmaß.
Insbesondere die Astronomie benützt als Raumwinkelmaßeinheiten sog. Quadratgrade
(bzw. Gradminutenquadrate und Gradsekundenquadrate), wobei ein Quadratgrad =
(π/180°)² ≈ 0,0003046 sr entspricht. Die Himmelskugel hat dann etwa 41 252,96
Quadratgrade -> http://home.att.net/~numericana/answer/angles.htm/solid
http://mathworld.wolfram.com/Steradian.html
2
Von griechischen Stereo [man denke an Raum(klang)] und Radiand, abgekürzt sr. Der
volle Raumwinkel 4π entspricht somit etwa 12,75 sr.
www.Udo-Rehle.de
2
25.03.2014
ein: Der Oktand ist nun der achte Teil der Oberfläche 4π der Kugel mit
dem Einheits-Radius. „Rechte Winkel“ haben also im Dreidimensionalen
weiterhin die Größe ½π.3
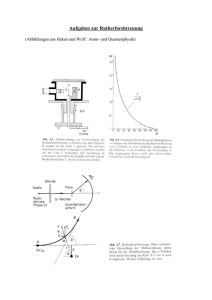
Abb. 1: Raumwinkel Ω = sphärische Fläche = ∫φ∫θ sin θ dθ dφ
bzw. die durch r² geteilte Fläche4
Oberen Abbildung mittig und rechts:
Der über einer der 4 Dreiecksseiten liegende und vom Zentrum der regelmäßigen
Dreieckspyramide aus betrachtete Raumwinkel ist genau 4 π:4=π.
Der Winkel „über einer Quadratseite“ ist5 4π/6 = ⅔π
3
Dass dies aber nicht für alle Dimensionen gilt, zeigt schon das Vierdimensionale:
Vierdimensionale rechte Winkel (von vier Halbräumen begrenzt bzw. von den vier
senkrecht aufeinander stehenden Koordinatenräumen aufgespannt, die nun den
gesamten Raum in 16 gleichgroße Teile zerlegen) sind nun ⅛π² groß!
4
Zur Raumwinkelberechnung über A/r² kann man die Integralrechnung zur Berechnung
des Kugeloberflächeteils A verwenden, wobei man dann noch auf die Einheitskugel
„normieren“ muss
http://www.math.cornell.edu/~hatcher/Other/hopf-samelson.pdf.
Für nähere Einzelheiten siehe >>Sphärische Trigonometrie<< oder suche in einer
Suchmaschine z.B. nach „steradian angles“ oder „solid angles“.
5
Detaillierter bei - http://mathworld.wolfram.com/SolidAngle.html
www.Udo-Rehle.de
3
25.03.2014
Zur genauen Berechnung von Raumwinkeln muss man also integrieren.
In Kugelkoordinaten (mit x = r sin θ cos φ, y = r sin θ sin φ , z = r cos θ)
ist dabei über zwei Winkel zu integrieren, wobei eben noch der Sinus des
einen Winkels dazu kommt.
Abb. 2: Raumwinkel des regelmäßigen Tetraeders
Wäre die Raumwinkelsumme auch π
wie die Summe der 3 ebnen Winkel des Dreiecks -,
dann müsste die schraffierte Fläche
die Hälfte der Achtelsphäre (=½π), nämlich ¼π sein!
(schraffierte Fläche wäre gleich der gelben Oktandenrestfläche)
-
www.Udo-Rehle.de
4
25.03.2014
Wenn es sich bei dem „Kugelsegment“ um ein Kugeldreieck handelt
(=
Eingrenzung
durch
drei
Großkreise),
dann
ist
das
Maß
des
Raumwinkels gerade der sog. sphärische Exzess ε (= die Abweichung der
Winkelsumme vom euklidischen Wert Pi; die Winkelsumme ist ja auf der
Kugel stets größer als Pi), da wir uns auf der Einheitssphäre befinden.
Die Fläche des Dreiecks A = ε R ist direkt proportional zur
Abweichung von der Euklidizität, d.h. durch den sog. sphärischen
Exzess ε6 bestimmt. Wegen R =1 ist der Raumwinkel also ε (sonst mit Ω
bezeichnet).
Raumwinkel ε = α+β+γ – π.
Eine andere Möglichkeit bietet die Formel von L´Huilier7
tan (¼ε) = √[(tan{¼(α+β+γ)} tan{¼(-α+β+γ)} tan{¼(α-β+γ)} tan{¼(α+β-γ)}]
Im Falle des regelmäßigen Tetraeders sind α=β=γ=60°, sprich ⅓π.
Damit wird tan ¼π = 1 mal tan³ 1/12 π etwa 0.02 und ein TetraederRaumwinkel ε ≈ 0,55, also deutlich kleiner als ¼π ≈ 0,785. Tatsächlich ist
er 3 cos-1 ⅓
6
7
8
-
π ≈ 0.551298. Die Raumwinkelsumme ist etwa 2,205.
ε (sprich Epsilon) ist griechischer Buchstabe für e
http://mathworld.wolfram.com/SphericalTrigonometry.html
- I Buch letztes Kapitel 21 >>STELL DIR VOR, DIE WEHRLE-FORMEL IST FALSCH<<
http://mathworld.wolfram.com/Tetrahedron.html
www.Udo-Rehle.de
5
25.03.2014
Berechnen wir den Raumwinkel der regelmäßigen Dreieckspyramide
näherungsweise durch die Berechnung des gleichseitigen Kugeldreiecks
auf der Einheitskugeloberfläche (in der vorigen Abbildung schraffiert; die
Würfelkantenlänge
ist
übrigens
a=1/√3
und
das
Volumen
des
TETRAEDERS ist ein Drittel des Würfelvolumens):
Kugeldreiecksfläche ist etwa ½ Grundlinienbogen mal Höhenbogen.
Kugeldreieck-Grundseite ist 2π:6= ⅓π ≈ 1.047
ε = A ≈ ½ (2π/6)
Höhenbogen
Das Kugeldreieck kann durch ein ebenes Sehnendreieck angenähert
werden: Der Bogen ist das Doppelte des zum Sinus gehörenden halben
Winkels im Bogenmaß:
a=2sin-1 Π:6 = 1.102
(Sehnendreieck von Bogendreieck der Bogenlänge ⅓π)
Da die Höhe des zugehörigen regelmäßigen Dreiecks des ebenen Dreiecks
½a√3 ist, ist also der Bogen zu ½√3 x 1.102 auszurechnen:
½a√3= 0.954 ist die geradlinige Höhe des ebenen Dreiecks
womit 2sin-1 0,4975 = 0.995 wird
also
½x0.995x1.047 ≈ 0.5209
also für einen Tetraederraumwinkel ε ≈ 0,52 (zum Vergleich ¼π ≈ 0,785)
ergäbe.
Somit wäre die Winkelsumme der vier Raumwinkel9 mit etwa 2.08
etwas über zwei statt der erwarteten 3,1416
9
Schon der Universalgelehrte Abbé Jean-Paul de Gua de Malves (1712-1786) stellte
Sätze zur Summe der 4 Raumwinkel auf!
Didaktik der Mathematik, 11. Jahrgang 1983 von R Fritsch – 1983 Egger u.a.:
Zum Winkelsummensatz für Tetraeder: http://epub.ub.uni-muenchen.de/4533/1/4533.pdf
www.Udo-Rehle.de
6
25.03.2014
Mit der Formel de L´Huilier ist die RW-Summe etwa 2,2 und jedenfalls
deutlich kleiner als π! Vorbei wohl also der Traum von einer konstanten
Winkelsumme aller Raumwinkel eines Polyeders!
Der regelmäßige Oktaeder ist in zwei quadratische Pyramiden zerlegbar
oder in acht sich im Zentrum berührender rechtwinklig-gleichschenkliger
Eulertetraeder) und hätte demgemäß die Winkelsumme 8π – 4π = 4π, dieselbe Winkelsumme wie beim Quader. Jeder einzelne seiner sechs
gleichgroßen
Raumwinkel
wäre
daher
⅔π
(Wenn
man
als
seine
Raumdiagonalenlänge zwei (und somit R=1) wählt, erhält man gerade die
Einheitskugel als Umkugel. Er teilte diese in acht gleiche symmetrischrechtwinklige Pyramiden mit den Winkeln ½π und den vermuteten
wobei
viermal
1/6π
1/6π;
eben ⅔π ergäbe). Der Oktaederwinkel lässt sich
halbieren zu einem der drei gleichen Raumwinkel eines Eulerschen mit
drei gleichen Katheten:
Der (nicht-rechte) Winkel des gleichschenkligen Euler-Tetraeders hat die
ebenen Begrenzungswinkel α=β=45° = ¼π und γ = 60°= ⅓π
Damit wird tan ¼Winkelsumme zum tan 5/24 π ≈ 0,767
und die Tangenswerte des Viertels der Differenzen sind zweimal
tan 1/12 π ≈ 0,268 und einmal tan 1/24 π ≈ 0,132, was einen
Raumwinkel von etwa 0,33 ergibt, während π/6 ≈ 0,52 ist!
Einer der drei gleichen Raumwinkel ist also eher 1/10 Pi. Damit wäre die
Raumwinkelsumme dieses am zweit-regelmäßigsten Tetraeders etwa 3
mal 0,33 + ½π
≈ 2,56, was auch deutlich kleiner als Pi ≈3.1416
Ein Oktaederraumwinkel ist der Raumspitzenwinkel einer quadratischen
Pyramide der Seitenlänge a mit der Höhe h= a: √2, für die folgende
Formel gilt:10
ε = 4 sin-1 a²/(a²+4h²)
10
http://planetmath.org/encyclopedia/FullSolidAngle.htm
www.Udo-Rehle.de
7
25.03.2014
ε = 4 sin-1 1/3
etwa 1,36 (vier mal 0.33)
Die Raum-Winkelsumme beim Oktaeder wäre das Sechsfache
und somit etwa 8,154.
also etwa nur das 2,6-fache von Pi ist
( 12,57 wäre genau 4Pi )
Für den inneren Raumwinkel eines Tetraeders, der von den Kanten OA=a,
OB=b und OC=c begrenzt wird, folgt die Formel von A. van Oosterom und
J. Strackee11 (1983):
tan (½ε) = |Det a b c| / [ abc + ab c + ac b + bc a]
a, b und c sind Ortsvektor zum Punkt A, B und C,
wobei der zu berechnende Raumwinkel im Ursprung beginnt.
Fett geschriebene Buchstaben sind dabei Vektoren,
beispielsweise ist ab c das Skalarprodukt der Vektoren a und b
multipliziert mit der Länge des Vektors c (c ist nicht fett).
Wenden wir das auf das Beispiel des regelmäßigen Tetraeders an, den wir
aus
jeder
zweiten
Koordinaten (
Ecke
des
Einheitswürfels
bilden.
Dessen
Eck-
Abb. 2) sind neben dem Ursprung (1, 1, 0), (1, 0 ,1) und
(0, 1, 1). Alle Kanten sind Flächenquadrat-Diagonalen der Länge
a = b = c =√2.
Die Determinante ist
1
Det 1
0
0
1
1
1
0 =2
1
Denn nach Sarrus ist (Summe und Differenz der Diagonalprodukte)
11
http://planetmath.org/encyclopedia/FullSolidAngle.htm
http://en.wikipedia.org/wiki/Solid_angle
www.Udo-Rehle.de
8
25.03.2014
1
1
0
0 1
1 0
1 1
1 0
1 1 = 1+ 0 +1 -0-0-0
0 1
Oder mit der Entwicklung nach Unterdeterminanten
1 0
Det 1 1 mal 1
-
1
Det 0
0
1
mal 0 +
1 1
Det 0 1
mal 1 = 1+1 =2
Das Skalarprodukt zweier Vektoren ist jeweils 1;
z.B.
1
0
1
mal 1
= 1x0+1x1+0x1 =
0
1
1
Somit wird
|Det a b c| / [ abc + ab c + ac b + bc a]
= 2 / (√2³ + √2 + √2 + √2) = √2 /5
Damit ist die Hälfte des-Raumwinkles eines reg. Teraeder
½ε = tan-1(√2 /5)≈0,272564
und ein Winkel also ≈ 0,5512856
was eine Raumwinkelsumme von 2,205142394 ergibt,
im Vergleich zu π= 3,141592654
Ist die Winkelsumme bei „spitzwinkligen“ Dreieckspyramiden immer
kleiner als Pi, und dabei umso größer, je unregelmäßiger der Tetraeder
ist? Bei stumpfwinkligen wird sie schnell größer als Pi aber kleiner als der
Halbraumwinkel 2 Pi.
Jedenfalls ist in einem Tetraeder die Summe der Raumwinkel ∑Rα
nicht konstant und kleiner als 2 Pi:
∑Rα < 2π
Ich behauptete zuvor, dass die Raumwinkelsumme genauso wie die
Winkelsumme beim ebenen Dreieck Pi sei. Beim Dreieck ist das eine
www.Udo-Rehle.de
9
25.03.2014
direkte Folge des Parallelenpostulats und ganz einfach zu beweisen. Wenn
man durch eine Ecke eine Parallele zur Gegenseite zieht. Aber die
Euklidische
ist
eben
nicht
die
Realität,
und
ebenso
wie
die
Raumwinkelsumme ist auch die Dreieckswinkelsumme in der Realität nicht
konstant, sondern, wie ich behaupte, immer größer als Pi (elliptische
Geometrie). Winkel und Seiten sind nämlich Dualitäten und jede Seite ist
nur das Bogenmaß eines Winkels (wenn man durch den entsprechenden
Kugelradius teilt -
I,21 STELL DIR VOR, DIE WEHRLE-FORMEL IST FALSCH).
Nun eine weitergehende Betrachtung, die mit den Kantenwinkeln12
zusammenhängt. Die Dreiecksflächen bilden einen jeweils einen Winkel,
den man Kantenwinkel13 („der Winkel zwischen den Normalen der sich
schneidenden Ebenen“) nennt. Vo denen gibt es in einem Tetraeder sechs,
wobei der 6. durch 5 Kantenwinkel eindeutig bestimmt ist. Aber was ist
die Kantenwinkelsumme K? Sie liegt zwischen 2π und 3π.
2π < K < 3π
12
Manche nennen diese auch Flächenwinkel. Auch die totale Winkeldefektsumme
Descartes T ist 4π, nämlich 2π mal der Eulerzahl Ecken-Kanten+Flächen.
Wird bei der Berechnung der relativen Winkel jeder Raumwinkel durch 4π, jeder
Flächenwinkel oder Kantenwinkel durch 2π geteilt, spricht man von den relativen
Raumwinkeln r, den relativen Flächenwinkeln f und den relativen Kantenwinkeln k
Σr – Σf + Σk = 1
Dieser Ausdruck erinnert an die Eulerformel, was kein Zufall ist:
T = 2π(Ecken-Kanten+Flächen)
EIDGENÖSSISCHE TECHNISCHE HOCHSCHULE ZÜRICH ETH
Zwei Fallstudien zur Geometrie von H~R.SChneebeli
--- www.educ.ethz.ch/unt/um/mathe/gb/Geometrie.pdf
http://mathworld.wolfram.com/AngularDefect.html
http://mathworld.wolfram.com/DescartesTotalAngularDefect.html
http://mathworld.wolfram.com/SphericalDefect.html
und http://www.geom.uiuc.edu/docs/doyle/mpls/handouts/node19.html#SECTION000190000000000000000
13
Lazare Carnot (1753-1823) hat wohl auch als erster 1806 diverse
Determinantenbedingungen für die Kantenwinkel eines Tetraeders aufgestellt.
www.Udo-Rehle.de
10
25.03.2014
Ferner besteht ein Tetraeder ja aus vier Dreiecken mit jeweils der
Winkelsumme Pi. Somit ist die Summe der Ebenenwinkel E also 4π.
E = 4π
(ebenso wie die Defektsumme T =4 π)
In einem Tetraeder ist die Summe der 4 Raumwinkel und der 12 ebenen
Winkel gleich der doppelten Summe der 6 Kantenwinkel:
R+E = 2K.
www.Udo-Rehle.de
11
25.03.2014