Klausur ET2 / MT/PT SS05-- P2

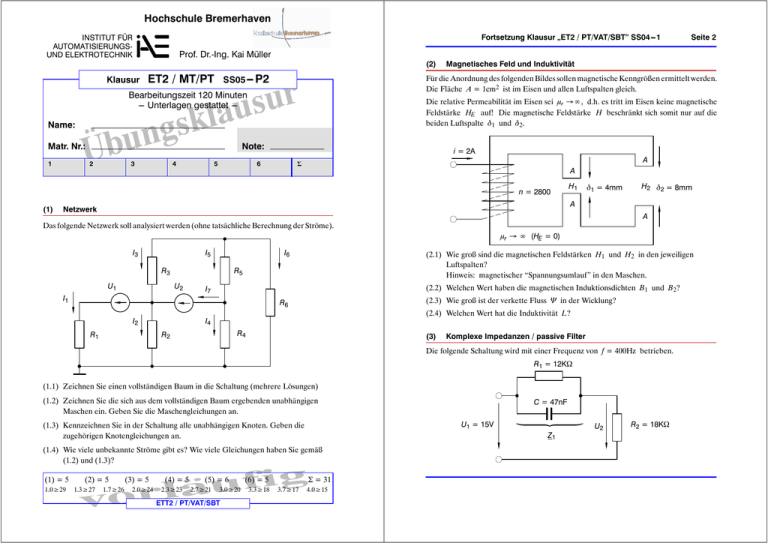
Hochschule Bremerhaven
Fortsetzung Klausur „ET2 / PT/VAT/SBT” SS04---1
INSTITUT FÜR
AUTOMATISIERUNGSUND ELEKTROTECHNIK
Prof. Dr.-Ing. Kai Müller
Klausur
ET2 / MT/PT
(2)
SS05 -- P2
Die relative Permeabilität im Eisen sei μr →∞, d.h. es tritt im Eisen keine magnetische
Feldstärke HE auf! Die magnetische Feldstärke H beschränkt sich somit nur auf die
beiden Luftspalte δ1 und δ2.
Name:
1
Note:
2
3
4
5
Magnetisches Feld und Induktivität
Für die Anordnung des folgenden Bildes sollen magnetische Kenngrößen ermittelt werden.
Die Fläche A = 1cm2 ist im Eisen und allen Luftspalten gleich.
Bearbeitungszeit 120 Minuten
--- Unterlagen gestattet ---
Matr. Nr.:
i = 2A
6
A
Σ
A
n = 2800
(1)
Seite 2
H1
δ1 = 4mm
H2 δ2 = 8mm
A
Netzwerk
A
Das folgende Netzwerk soll analysiert werden (ohne tatsächliche Berechnung der Ströme).
μr → ∞ (HE = 0)
I3
I5
I6
R3
U1
(2.1) Wie groß sind die magnetischen Feldstärken H1 und H2 in den jeweiligen
Luftspalten?
Hinweis: magnetischer “Spannungsumlauf” in den Maschen.
R5
U2
I1
(2.2) Welchen Wert haben die magnetischen Induktionsdichten B1 und B2?
I7
(2.3) Wie groß ist der verkette Fluss Ψ in der Wicklung?
R6
I2
R4
R2
R1
(2.4) Welchen Wert hat die Induktivität L?
I4
(3)
Komplexe Impedanzen / passive Filter
Die folgende Schaltung wird mit einer Frequenz von f = 400Hz betrieben.
R1 = 12KΩ
(1.1) Zeichnen Sie einen vollständigen Baum in die Schaltung (mehrere Lösungen)
(1.2) Zeichnen Sie die sich aus dem vollständigen Baum ergebenden unabhängigen
Maschen ein. Geben Sie die Maschengleichungen an.
U1 = 15V
(1.3) Kennzeichnen Sie in der Schaltung alle unabhängigen Knoten. Geben die
zugehörigen Knotengleichungen an.
(1.4) Wie viele unbekannte Ströme gibt es? Wie viele Gleichungen haben Sie gemäß
(1.2) und (1.3)?
(1) = 5
1.0≥29
(2) = 5
1.3≥27
1.7≥26
(3) = 5
2.0≥24
(4) = 5
2.3≥23
(5) = 6
2.7≥21
3.0≥20
ETT2 / PT/VAT/SBT
(6) = 5
3.3≥18
Σ = 31
3.7≥17
C = 47nF
4.0≥15
Z1
U2
R2 = 18KΩ
Fortsetzung Klausur „ET2 / PT/VAT/SBT” SS04---1
Seite 3
(3.1) Geben Sie die komplexe Impedanz Z1 für die Parallelschaltung aus Widerstand
und Kondensator an.
(3.2) Bestimmen Sie die Spannung U2 . (U1 = 15V ist reell).
Hinweis: Bestimmen Sie Zähler und Nenner getrennt und berechnen Sie dann die
komplexe Lösung.
Fortsetzung Klausur „ET2 / PT/VAT/SBT” SS04---1
Seite 4
Die Werte seien R = 15Ω, L1 = 6mH, L2 = 18mH, f = 50Hz.
(5.1) Berechnen Sie den Strom I.
(5.2) Bestimmen Sie die Spannung an der Last bestehend aus L2 und R.
(5.3) Geben Sie die komplexe Scheinleistung S für die Last an.
(3.3) Wie groß wird U2 für ω → ∞ ?
(6)
(4)
Zeigerdiagramm
I
Leistung in einem Drehstromsystem
Ein einem symmetrischen Drehstromsystem werden alle Phasen mit einer ohmsch-induktiven Last betrieben.
U1
Die Werte seien R = 82Ω, L = 60mH. Alle Phasenspannungen betragen 230V.
C (für jede Phase)
L
C
U0
R
U2
U1
R
L
R
L
R
L
L1
U2
L2
Die Werte seien U0 = 10V (reell), R = 680Ω, C = 12nF, L = 2mH, f = 40kHz.
(4.1) Welchen Wert haben die Spannungen U1 und U2?
U3
(4.2) Wie groß ist I?
L3
(4.3) Welchen Winkel zwischen der Spannung U0 und dem Strom I ergibt sich?
(4.4) Zeichnen Sie ein Zeigerdiagramm mit alle Größen.
(5)
N
De Kondensatoren bleiben für die Aufgabe (6.1) unberücksichtigt.
Komplexe Scheinleistung
I
(6.1) Bestimmen Sie die gesamte Wirk- und Blindleistung über die komplexe
Scheinleistung S.
L1
(6.2) Welchen Wert müssen die Kondensatoren erhalten, damit die induktive
Blindleistung kompensiert wird?
L2
U1 = 115V
(reell)
(6.3) Wir groß wird dann die Wirkleistung?
U2
Last
R
:::