Gegeben ist ein lineares Netzwerk mit der Spannung U0 und den
Werbung

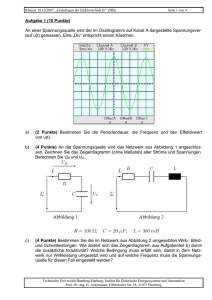
· Universität Siegen Grundlagen der Elektrotechnik für Maschinenbauer Fachbereich 12 Prüfer : Dr.-Ing. Klaus Teichmann Datum : 30. 3. 2006 Klausurdauer : 2 Stunden Hilfsmittel : 5 Blätter Formelsammlung DIN A4, Taschenrechner Name (lesbar) : Matrikel-Nr. : Studiengang bitte ankreuzen Maschinenbau Wirtschaftsingenieurwesen Internationale Projektierung Angewandte Informatik : Aufgabe 1 2 3 4 5 6 Summe Mögliche Punkte 14 17 20 19 19 15 104 Note Erreichte Punkte 1. Aufgabe (Kondensator) (14 Punkte) Gegeben ist ein Kondensator, mit einer Kapazität von 300µF, der auf eine Spannung von 300V aufgeladen ist. 1) Wie viel Ladung ist im Kondensator gespeichert? (2 Punkte) 2) Wie groß ist die Energie, die im elektrischen Feld des Kondensators gespeichert ist? (2 Punkte) 3) Welcher Zusammenhang besteht allgemein zwischen der Spannung an einer Kapazität und dem Strom (Verschiebungsstrom) durch die Kapazität? Geben Sie eine Schaltung mit Zählpfeilen für Spannung und Strom an. (3 Punkte) 4) Wie groß ist die Spannung, die bei dem oben gegebenen Zustand an der Induktivität anliegt? (2 Punkte) 5) Wie groß ist ein konstanter Strom, der den Kondensator in 20ms von 100% seiner Anfangsspannung auf 30% seiner Anfangsspannung entlädt, bezogen auf die in der Teilaufgabe 3 angegebenen Zählpfeile? (5 Punkte) Klausur Grundlagen der Elektrotechnik für Maschinenbauer vom 30. 3. 2006 Seite 1 2. Aufgabe (Lineares Netzwerk) (17 Punkte) Gegeben ist ein lineares Netzwerk mit der Spannung U0 und den Widerständen RA bis RG, entsprechend Bild 1. Bild 1: Lineares Widerstandsnetzwerk a) Bestimmen Sie die Ströme I0, IA, und IF b) Bestimmen Sie die Spannungen UA, UB und UF (12 Punkte) (3 Punkte) c) Überprüfen Sie die Plausibilität ihrer Ergebnisse indem sie einen Spannungsumlauf kontrollieren. (2 Punkte) Klausur Grundlagen der Elektrotechnik für Maschinenbauer vom 30. 3. 2006 Seite 2 3. Aufgabe: (Kirchhoff-Verfahren) (20 Punkte) Gegeben ist die in Bild 2 dargestellte Schaltung. R1 I1 I3 IQA UQA R3 I2 R2 R4 R6 I4 R5 UQB IQB I5 Bild 2: Schaltbild zu Aufgabe 3 Erstellen Sie nach der Kirchhoff-Methode eine Matrizengleichung, nach deren Lösung sich die Ströme I1 bis I5 und IQ1 und IQ2 bestimmen lassen. (20 Punkte) Zur Klarstellung: Es geht nur darum das Gleichungssystem aufzustellen; es geht nicht darum es zu lösen. Hinweis: Sie können annehmen, dass die Widerstände und die Spannungsquellen bekannt sind. 4. Aufgabe: (Wechselstromverbraucher) (19 Punkte) Eine Spannungsquelle (Wechselspannung) UQ versorgt einen ohmsch-induktiven Verbraucher, der sich als Parallelschaltung eines Widerstands R und einer Spule L darstellen lässt. Die gemessene Spannung beträgt UQ=220V. Mittels eines Amperemeters wird der Strom aus der Spannungsquelle zu IQ=20A gemessen. Der Leistungsfaktor des Verbrauchers beträgt 0,8. a) Zeichnen Sie das Schaltbild der Anordnung und tragen Sie Zählpfeile für die Spannung und die Ströme ein. (4 Punkte) b) Skizzieren Sie qualitativ das Zeigerbild der Leistungen. (3 Punkte) c) Wie groß ist die Scheinleistung? (2 Punkt) d) Wie groß ist die Wirkleistung? (2 Punkt) e) Wie groß ist die Blindleistung? (2 Punkt) f) Wie groß ist der Widerstand R? (2 Punkte) g) Wie groß ist die Reaktanz XL der Spule (2 Punkte) h) Wie groß muss die Reaktanz XC eines Kondensators sein, um den Gesamtleistungsfaktor auf cos ϕg=1 zu verbessern. (2 Punkt) Klausur Grundlagen der Elektrotechnik für Maschinenbauer vom 30. 3. 2006 Seite 3 5. Aufgabe (Unsymmetrische Drehstromlast) (19 Punkte) Eine symmetrische Spannungsquelle UL1, UL2, UL3 versorgt einen unsymmetrischen Verbraucher, der aus nur einer Impedanz ZV31 besteht, die, wie im Bild 3 dargestellt, zwischen den Leitern des Drehspannungssystems angeschlossen ist. IL1V UL1L2 UL1 ZV31 UL3L1 UL2 UL2L3 UL3 IL2V IL3V Bild 3: Schaltung zu Aufgabe 5 Bekannt sind die Spannungsquellen U L1 = 220V ⋅ e j 30° U L 2 = 220V ⋅ e − j 90° U L3 = 220V ⋅ e j150° und die Impedanz Z V 31 = (3 + j 4)Ω = 5Ω ⋅ e + j 53,13° a) Wie lauten die komplexe Spannungen an der Impedanz UV31 ? Tragen Sie den Zählpfeil für die Spannung UV31 im Bild ein. (4 Punkte) (1 Punkt) b) Berechnen Sie den komplexen Strom durch die Impedanz. (2 Punkte) (Hinweis: Beachten Sie die im Bild gegebenen Zählpfeile) c) Welche komplexe Scheinleistung wird in der Impedanz ZV31 umgesetzt? (3 Punkte) d) Welche komplexen Scheinleistungen werden in den Spannungsquellen umgesetzt? (5 Punkte) e) Prüfen Sie im Komplexen, ob die verbrauchte Scheinleistung gleich der erzeugten Scheinleistung ist. (4 Punkte) Klausur Grundlagen der Elektrotechnik für Maschinenbauer vom 30. 3. 2006 Seite 4 6. Aufgabe (Fragen) (15 Punkte) 1. Wie viel Joule entsprechen einer Kilowattstunde? (2 Punkte) 2. Wie ist der Zusammenhang zwischen elektrischem Strom und transportierter Ladung? (2 Punkte) 3. Zum Trennen von Ladungen wird Energie benötigt. Wie groß ist die Spannung zwischen einer positiven und einer negativen Ladung von 2 As, wenn zu ihrer Trennung eine Energie von 1MJ aufgewendet werden musste? (Es handele sich um einen verlustfreien Vorgang.) (2 Punkte) 4. In einem bekannten Vektorfeld E sind zwei Punkte P1 und P2 gegeben. Wie groß ist die Spannung zwischen den beiden Punkten? 5. Zeichnen Sie einige magnetische Feldlinien im Eisenkern ein und geben Sie deren Orientierung an. (2 Punkte) . . ( 3 Punkte) 6. In einem 1 Meter langen Leiterstück fließt ein Strom von I=1A durch ein Magnetfeld mit der Flussdichte B=1T. Stromrichtung und die Richtung des magnetischen Feldes sind identisch. Wie groß ist die Kraft auf das Leiterstück? (4 Punkte) Eisenkern I Klausur Grundlagen der Elektrotechnik für Maschinenbauer vom 30. 3. 2006 Seite 5