Variation - HS Vossbarg

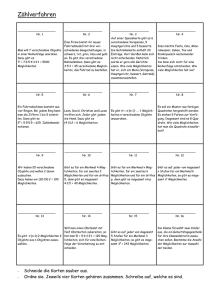
Mathematik – Stochastik – Kombinatorik – Variation – Sellmer
Variation
Bei einer Permutation sind alle auftretenden Elemente beteiligt. Bei einer Variation (und Kombination)
ist nur eine bestimmte Anzahl k aus den n Elementen beteiligt. Wenn diese Reihenfolge wichtig ist,
dann spricht man von einer Variation.
Variation
Mit Wiederholung
Ohne Wiederholung
Zur Berechnung von Variationen ohne Wiederholung benötigt man die Fakultät. Fakultät wird
mit dem Ausrufezeichen angegeben und bedeutet, dass alle ganzen Zahlen bis zur
Fakultätszahl miteinander multipliziert werden. So ist z.B.: 5! = 5  4  3  2  1 = 120
Beispiel: Variation mit Wiederholung
 Ein Zahlenschloss hat eine vierstellige Nummer. Auf jedem
Ziffernrad befinden sich die Ziffern von 1 bis 6. Wie viele
verschiedene Zahlen kann man einstellen?
Lösung:
Bei einer Zahl mit vier Ziffern ist k = 4. Jedes Ziffernrad hat sechs verschiedene Ziffern (von 1 bis 6),
somit ist n = 6. Durch das Einsetzen in die Formel erhalten wir nk = 64 = 1296. Somit sind also 1296
verschiedene Zahlen auf dem Zahlenschloss einstellbar.
 In einer Box befinden sich 3 Kugeln, die mit „A“, „B“ und „C“ beschriftet sind. Es wird sechsmal
hintereinander eine Kugel gezogen und wieder zurück gelegt. Wie viele „Wortkombinationen“ sind
möglich?
Lösung:
Bei einem „Wort“ mit sechs Buchstaben ist k = 6. Jede Stelle
des Wortes hat drei Möglichkeiten „A“, „B“ oder „C“, somit ist n
= 3. Durch das Einsetzen in die Formel erhalten wir nk = 36 =
729. Somit sind also 729 verschiedene Worte möglich.
︶
=
! !
5 2
=
︶︵
!
! 3
55
!
︵
k
!n
n
Beispiel: Variation ohne Wiederholung
 Beim Kugelstoßwettbewerb treten Alex, Bert, Caesar, Daniel und Emil
gegeneinander an. Für die Schülerzeitung soll ein Bild mit den drei Siegern
auf dem Siegerpodest gemacht werden. Wie viele Möglichkeiten für die
Zusammensetzung der drei Gewinner gibt es?
Lösung:
Da alle Elemente (Teilnehmer) verschieden sind, ist n = 5. Auf dem Podest gibt es drei Plätze (Gold,
Silber und Bronze), somit ist k = 3. Durch das Einsetzen in die Formel erhalten wir:
= 5  4  3 = 60. Es sind also 60 verschiedene Photos möglich.
︶
=
!
0 !
1 7
=
︶︵
!
! 3
01 0
1
!
wir:
︵
k
!n
n
 Bei einem Pferderennen kann man eine „Dreierwette“ abschließen, d.h. man wettet darauf, welches
Pferd als erstes, welches als zweites und welches als drittes Pferd über die Ziellinie läuft. Wie viele
Möglichkeiten für eine Dreierwette gibt es, wenn 10 Pferde starten?
Lösung:
Da alle Elemente (hier die Pferde) verschieden sind, ist n = 10. Die ersten drei
Einläufe sind relevant, also ist k = 3. Durch das Einsetzen in die Formel erhalten
= 10

9

8 = 720. Es gibt also 720 Möglichkeiten
für eine Dreierwette bei einem Pferderennen mit 10 Pferden.