Aufgabenblatt Fadenpendel und Ramme
Werbung
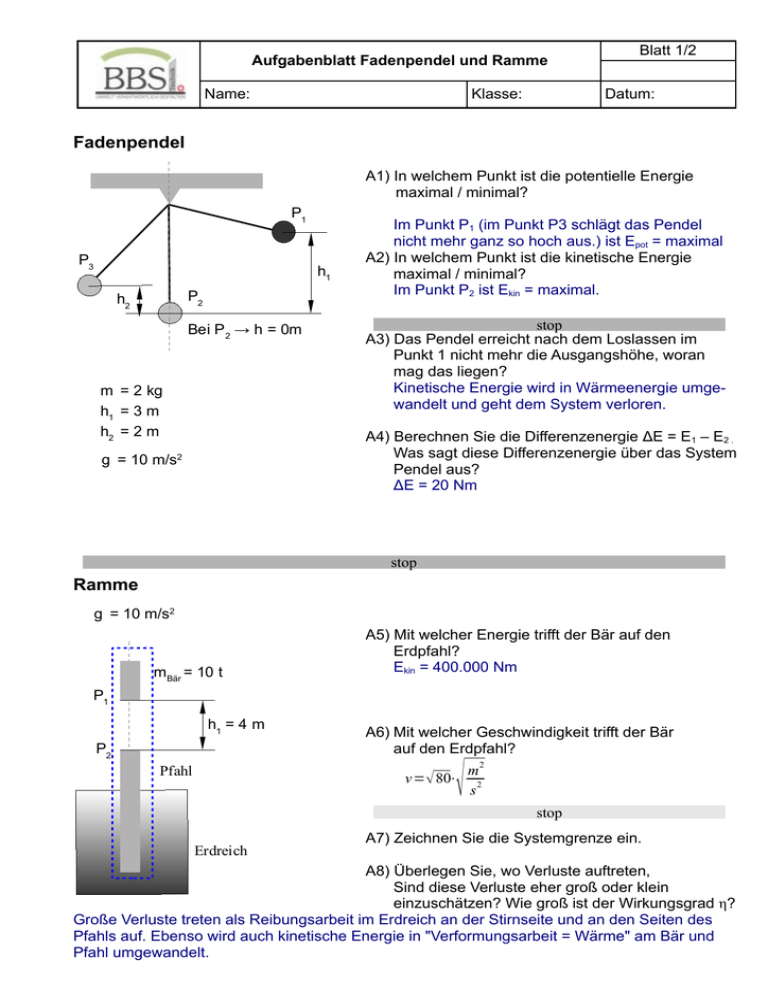
Aufgabenblatt Fadenpendel und Ramme Name: Klasse: Blatt 1/2 Datum: Fadenpendel A1) In welchem Punkt ist die potentielle Energie maximal / minimal? P1 P3 h1 P2 h2 Bei P 2 → h = 0m m = 2 kg h1 = 3 m h2 = 2 m Im Punkt P1 (im Punkt P3 schlägt das Pendel nicht mehr ganz so hoch aus.) ist Epot = maximal A2) In welchem Punkt ist die kinetische Energie maximal / minimal? Im Punkt P2 ist Ekin = maximal. stop A3) Das Pendel erreicht nach dem Loslassen im Punkt 1 nicht mehr die Ausgangshöhe, woran mag das liegen? Kinetische Energie wird in Wärmeenergie umgewandelt und geht dem System verloren. A4) Berechnen Sie die Differenzenergie ΔE = E1 – E2 . Was sagt diese Differenzenergie über das System Pendel aus? ΔE = 20 Nm g = 10 m/s2 stop Ramme g = 10 m/s2 mBär = 10 t A5) Mit welcher Energie trifft der Bär auf den Erdpfahl? Ekin = 400.000 Nm P1 h1 = 4 m P2 A6) Mit welcher Geschwindigkeit trifft der Bär auf den Erdpfahl? Pfahl v= 80⋅ Erdreich 2 m 2 s stop A7) Zeichnen Sie die Systemgrenze ein. A8) Überlegen Sie, wo Verluste auftreten, Sind diese Verluste eher groß oder klein einzuschätzen? Wie groß ist der Wirkungsgrad η? Große Verluste treten als Reibungsarbeit im Erdreich an der Stirnseite und an den Seiten des Pfahls auf. Ebenso wird auch kinetische Energie in "Verformungsarbeit = Wärme" am Bär und Pfahl umgewandelt. Aufgabenblatt Fadenpendel und Ramme Name: Klasse: Blatt 2/2 Datum: Fadenpendel A1) In welchem Punkt ist die potentielle Energie maximal / minimal? P1 P3 h1 A2) In welchem Punkt ist die kinetische Energie maximal / minimal? P2 h2 Bei P 2 → h = 0m h1 = 3 m h2 = 2 m m = 2 kg g = 10 m/s2 stop A3) Das Pendel erreicht nach dem Loslassen im Punkt 1 nicht mehr die Ausgangshöhe, woran mag das liegen? A4) Berechnen Sie die Differenzenergie ΔE = E1 – E2 . Was sagt diese Differenzenergie über das System Pendel aus? stop Regenwolken als Energiespeicher Aus Regenwolken in 600 m Höhe fällt über einer Landfläche von 120 km² Regen mit einer Niederschlagshöhe von 12 mm. h = 600 m A5) Ermitteln Sie die in den Regenwolken enthaltende Energie der Lage dieser Wassermenge (die Dichte von Wasser ist 1,0 g/cm3 ). Epot = 8,48·1010 Nm g = 10 m/s2 A = 120 km² Niederschalgshöhe t = 12 mm A6) Die Regentropfen kommen mit der durchschnittlichen Geschwindigkeit von 6,0 m/s am Erdboden an. Bestimmen Sie den prozentualen Verlust an mechanischer Energie dieser Regentropfen. Wo ist diese Energie geblieben? η = 0,003 = 0,3% Die kinetische Energie wurde zum größten Teil während des Fallens in Reibungsarbeit (99,7%) umgesetzt!











