normale des

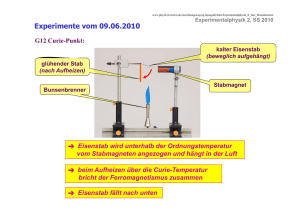
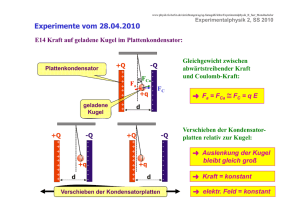
Zur Erinnerung
Stichworte aus der
12. Vorlesung:
Zusammenfassung:
Trägheitsmomente, Kreisel, etc.
allgemeine Darstellung des Drehimpulses für Drehung von
beliebig geformtem Körper um beliebige Drehachse (durch
den Schwerpunkt)
Zusammenhang von ω und L. Im allgemeinen Fall liegt L
nicht parallel zu ω.
Trägheitstensor: verbindet L mit ω („transformiert ω nach
L“ )
Hauptträgheitsachsen:
Trägheitsmomente:
Experimentalphysik I SS 20/11
Hauptträgheitsachsen = drei senkrecht zu einander
stehende Achsen a, b, c mit zugehörigen
Trägheitsmomenten Ia ≤ Ib ≤ Ic
12-1
Zur Erinnerung
(wenn zwei der Trägheitsmomente gleich sind:
symmetrischer Kreisel)
Trägheitsellipsoid:
Trägheits-Ellipsoid (aus Darstellung der Rotationsenergie
durch Trägheitstensor).
Wenn Ia, Ib und Ic bekannt, kann Iω für beliebige
Richtung der Drehachse ω bestimmt werden.
Rotation um nicht gelagerte Achsen: stabile Rotation nur
um die Achse c, d.h. die Achse mit dem größten
Trägheitsmoment
Kreisel:
Experimentalphysik I SS 20/11
Präzession
Nutation
Kreiselkompass
12-2
6. Eigenschaften nicht-starrer
(deformierbarer) fester Körper
Reale Körper:
ob fest – flüssig – gasförmig hängt wesentlich ab von der
Stärke der Atom-Atom Wechselwirkung im Vergleich zur
(siehe später) „mittleren thermischen Energie“
Experimentalphysik I SS 20/11
12-3
Übergang zwischen Aggregatzuständen
Fest
Kristalliner Festkörper
wohldefinierte Nahordnung durch gerichtete Bindung,
wohldefinierte Fernordnung.
(Amorpher Festkörper: keine Fernordnung, Richtungsabhängigkeit der Bindung läßt keine Kristallstruktur zu.)
Erhöhung der Temperatur (Energiezufuhr):
<Ekin> = ½ k T pro Freiheitsgrad (s. später) steigt,
wenn <Ekin> ≥ E* → Schmelzen.
Flüssig
Flüssig
Nahordnung vorhanden (ungerichtete atomare Bindung),
keine Fernordnung mehr.
Weitere Erhöhung der Temperatur:
wenn <Ekin> ≥ EBindung → Verdampfen.
Gasförmig
Gasförmige Substanz:
Weder Nahordnung noch Fernordnung vorhanden.
Individuelle, untereinander stoßende Teilchen.
Experimentalphysik I SS 20/11
12-4
Struktur von Festkörpern
Homogenität:
physikalische Eigenschaften im makroskopischen Maßstab
L >> a (wobei a = Atomabstand) überall gleich.
Isotropie:
physikalische Eigenschaften im makroskopischen Maßstab
unabhängig von der Richtung
Kristalline Strukturen (Stück Eisen, Salzkristall, Diamant)
sind in der Regel homogen, aber nicht isotrop.
Beispiele: Kristallwachstum, Spalten von Kristallen,
Doppelbrechung, Elektronenleitung in Halbleitern usw.
Amorphe Festkörper, flüssiges Material, Gas
sind in der Regel homogen und isotrop.
Gegenbeispiele: Nylon (gerichtete Molekülketten),
Emulsionen (insb. deren Zerfall),
Erdatmosphäre (auf der km-Skala).
Experimentalphysik I SS 20/11
12-5
Struktur von Festkörpern
Kristalline Struktur:
Atome sitzen auf Positionen, gegeben durch
ri  na ,i a  nb,i b  nc ,i c
Starre Verbindungen
ersetzt durch Federn:
Betrachtet werden:
1. Elastische (reversile)
Verformung
2. irreversible
Verformung
Experimentalphysik I SS 20/11
12-6
Deformierbare feste Körper
Allgemeines:
Dehnung eines Stabes:
Experimentalphysik I SS 20/11
12-7
Deformierbare feste Körper
Dehnung eines
Stabes:
Hook‘sches Gesetz:
Anmerkung: der Modul, die Moduln
Experimentalphysik I SS 20/11
12-8
Deformierbare feste Körper
Beispiel:
Dehnung eines Eisendrahtes
F  E q
L
L
„Atomares Bild“
typischer Abstand der Atome: 0.1 nm
bei L = 1 m 1010 Atome „in Reihe“
bei d ≈ 1 mm 107 Reihen parallel
Dehnung Atom-Atom-Abstand (einzeln)
Δr ≈ 0.1 nm 10-3 = 10-13 m,
vergleiche: Durchmesser Atomkern rK ≈ 10-15 m
Experimentalphysik I SS 20/11
12-9
Deformierbare feste Körper
Grenzen des
Hook‘schen Gesetzes:
  E 
„Atomares Bild“
d)
a)
b)
c)
a) Elastische Dehnung, b) Plastische Verformung
c) „Fließen“
d) Reißen
Experimentalphysik I SS 20/11
12-10
Querkontraktion
Experimentalphysik I SS 20/11
12-11
Querkontraktion
Experimentalphysik I SS 20/11
12-12
Hysterese
Arbeit bei der
periodischen
Streckung und
Stauchung um L:
(mit Substitution
ε = ΔL/L, dε = dL/L)
Elastische
Verformung:
(reversible) plastische
Verformung:
Experimentalphysik I SS 20/11
12-13
Kompression
)
Druckeinheit:
Im Labor („leicht“)
erreichbar 50 GPa

Experimentalphysik I SS 20/11
½ Mio bar
12-14
Scherung und Torsion
+
Experimentalphysik I SS 20/11
12-15
Torsion eines Drahtes
= Richtmoment
Experimentalphysik I SS 20/11
12-16
Torsion eines Drahtes
und


erforderliches
Drehmoment für
Verdrillung um ϕ:
R4
(Torsionsschwingungen, Messung von G)
r
D~R4
Experimentalphysik I SS 20/11
12-17
Zusammenhang zwischen den Moduln
σ=Eε
(Herleitung: GKV)
(s.o.)
κ = 1/K = Kompressibilität
Experimentalphysik I SS 20/11
12-18
Elastizitätskonstanten
Im Vorgriff, Wasser: K = 2x109 N/m2
Experimentalphysik I SS 20/11
12-19
Reibung
Reibung und
Oberfläche:
Experimentalphysik I SS 20/11
12-20
Reibung
≤
Haft-, Gleit- und
Rollreibung:
(Reibungskoeffizient)
Haftreibung:
Experimentalphysik I SS 20/11
12-21
Hydrostatik
Verhalten und Gesetze
ruhender
Flüssigkeiten
ideale Flüssigkeit:
keine elastische Dehnung möglich
keine Oberflächen-Effekte
später: Hydrodynamik: strömende Flüssigkeiten und
Gase, Reibungseffekte spielen eine Rolle
Kompressionsmodul: vergleichbar Festkörpern
Aber:
Schermodul G = 0, d.h. keine Tangentialkräfte FT

im stationären Zustand können keine TangentialKräfte auf die Oberfläche wirken
stationär:
Kraft  Oberfläche
Oberfläche einer idealen Flüssigkeit steht immer senkrecht
zu der auf die Flüssigkeit wirkenden Gesamtkraft
Experimentalphysik I SS 20/11
12-22
Hydrostatik
Oberfläche einer
rotierenden
Flüssigkeit:
Im stationären Zustand:
resultierende Kraft muss senkrecht zur Oberfläche
stehen (da G = 0)


Experimentalphysik I SS 20/11
Form der Oberfläche einer
rotierenden Flüssigkeit:
Paraboloid
12-23
Statischer Druck in Flüssigkeiten
Schermodul von Flüssigkeiten: G = 0
 freie Beweglichkeit der Moleküle
 nur Normalkomponente der Kraft F bezüglich Fläche A
kann zum Druck beitragen
Definition des
Druckes:
mit F = | Fn| wird p = F/A
Druck ist ein Skalar und
kein Vektor!!
Druck im
Flüssigkeitsvolumen:
Experimentalphysik I SS 20/11
12-24
Kräfte an der Oberfläche von Flüssigkeiten
in stationären Fall
stellt sich die Richtung
der Oberfläche so ein,
dass nur FN  0
z
FN
F
dA
y
Fx
Fy
x
dA = Normale des Flächenelementes
dA = Normale des Flächenelementes
Experimentalphysik I SS 20/11
12-25
Statischer Druck in Flüssigkeiten
Druck im
Flüssigkeitsvolumen
(bei Vernachlässigung
des Eigengewichtes)
Volumenelement dV = dx dy dz, Flächenelement dA = dy dz
p(x) = p bei Druckänderung p(x + dx) = p + (∂p/∂x) dx
damit wird Kraft Fx auf Flächenelement
Fx = p dy dz - (p + (∂p/∂x) dx) dy dz
Fx = - (∂p/∂x) dV entsprechend
Fy = - (∂p/∂y) dV, Fz = - (∂p/∂z) dV also
F = - (grad p) dV
Gesamtkraft auf ruhendes Flüssigkeitselement
(stationärer Zustand) F = 0 !
 grad p = 0,
p(x,y,z) = const.
 auf jedes Flächenelement dA wirkt die gleiche Kraft und
somit der gleiche Druck!
Experimentalphysik I SS 20/11
12-26
Statischer Druck in Flüssigkeiten
Hydraulische Presse:
Heben eines
schweren Gegenstandes der
Masse M um h
Arbeit W = M g h muss geleistet werden
jedoch: Kraft F = M g nicht notwendig, da p = const.
innerhalb der Flüssigkeit:
F1 = p A1 F2 = p A2 F1 = F2 (A1/A2)
(F1 << F2 )
allerdings muss gelten (Energieerhaltung) W1 = W2
also F1 s1 = F2 s2, daher s1 = (F2 / F1) s2
 s1 = (A2 / A1) s2
Experimentalphysik I SS 20/11
(s2 >> s1)
12-27