Entwicklung eines Steuerungssystems für

Andreas Blinzler & Andreas Hirschberger
Entwicklung eines Steuerungssystems
für Kraftfahrzeuge auf der Basis
evolutionärer Verfahren
Diplomarbeit
Georg-Simon-Ohm Fachhochschule Nürnberg
University of Applied Sciences
Fachbereich Informatik
Entwicklung eines Steuerungssystems für Kraftfahrzeuge auf der Basis
evolutionärer Verfahren
Diplomanden:
Andreas Blinzler & Andreas Hirschberger
1. Prüfer:
Prof. Dr. R. Eck
2. Prüfer:
Prof. Dr. C. Schiedermeier
Georg-Simon-Ohm Fachhochschule Nürnberg – University of Applied Sciences
Fachbereich Informatik, Diplomarbeit, 30. September 2005
Alles hat seine Stunde, und es gibt eine Zeit für jegliche Sache unter dem Himmel:
Eine Zeit für die Geburt und eine Zeit für das Sterben, eine Zeit zu pflanzen und
eine Zeit, das Gepflanzte auszureißen, eine Zeit zu töten und eine Zeit zu heilen,
eine Zeit einzureißen und eine Zeit aufzubauen;
Kohelet 3
Inhaltsverzeichnis
Vorwort
XVII
Projektdefinition
XIX
I. Theorie
1
1. Evolution und Genetik
1.1. Molekular- und Evolutionsgenetik . . . . . . . . . . . .
1.1.1. Chromosom . . . . . . . . . . . . . . . . . . . .
1.1.2. Zellteilung . . . . . . . . . . . . . . . . . . . . .
1.1.3. Genetische Information . . . . . . . . . . . . . .
1.1.4. Gen . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Evolutionsfaktoren und die Mechanismen der Evolution
1.2.1. Zufall . . . . . . . . . . . . . . . . . . . . . . .
1.2.2. Evolution von Populationen . . . . . . . . . . .
1.2.3. Populationswellen . . . . . . . . . . . . . . . . .
1.3. Evolution als Optimierungsprozess . . . . . . . . . . .
1.3.1. Evolution als kombinierte Suchstrategie . . . . .
1.3.2. Globale und lokale Optima . . . . . . . . . . . .
1.4. Konventionelle Optimierungsverfahren . . . . . . . . .
1.4.1. Deterministische Verfahren . . . . . . . . . . . .
1.4.2. Nicht deterministische Verfahren . . . . . . . .
3
4
4
4
5
6
7
7
7
8
8
9
10
11
11
13
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2. Evolutionsstrategien
15
2.1. Codierung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
V
Inhaltsverzeichnis
2.2. Varianten . . . . . . . . . . . . . . .
2.2.1. (1+1) - Evolutionsstrategie . .
2.2.2. (µ+λ) - Evolutionsstrategie .
2.2.3. (µ,λ) - Evolutionsstrategie . .
2.2.4. (µ#λ) - Evolutionsstrategie .
2.2.5. (µ/ρ#λ) - Evolutionsstrategie
2.3. Mutation . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3. Genetische Algorithmen
3.1. Beschreibung eines genetischen Algorithmus
3.2. Codierung . . . . . . . . . . . . . . . . . . .
3.2.1. Binärcode . . . . . . . . . . . . . . .
3.2.2. Länge . . . . . . . . . . . . . . . . .
3.2.3. Junk DNS . . . . . . . . . . . . . . .
3.3. Bewertung und Fitness . . . . . . . . . . . .
3.3.1. Proportionale Skalierung . . . . . . .
3.3.2. Lineare Skalierung . . . . . . . . . .
3.3.3. Dynamic Power Law Skalierung . . .
3.4. Genetische Operatoren . . . . . . . . . . . .
3.4.1. Selektions-Schema . . . . . . . . . .
3.4.2. Heirats-Schema . . . . . . . . . . . .
3.4.3. Rekombination der Chromosomen . .
3.4.4. Mutationen . . . . . . . . . . . . . .
3.4.5. Fortgeschrittene Operatoren . . . . .
3.5. Ersetzungsschema . . . . . . . . . . . . . . .
3.6. Kontrollgrößen . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4. Evolutionsstrategien kontra genetische Algorithmen
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
16
16
16
17
17
17
18
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
21
21
23
23
25
26
26
27
27
28
29
29
30
30
32
34
35
37
39
5. Evolution von Populationen
41
5.1. Insel-Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
5.2. Netzwerk-Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
5.3. Kommunen-Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
II. Software-Entwicklung
VI
45
Inhaltsverzeichnis
6. Server für evolutionäre Verfahren
6.1. Pakete . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2. Bibliothek für evolutionäre Algorithmen . . . . . . . . . . . . . . .
6.2.1. Komponenten . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2.2. Softwarearchitektur . . . . . . . . . . . . . . . . . . . . . . .
6.3. Server-Bibliothek . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3.1. Exkurs: Java Native Interface . . . . . . . . . . . . . . . . .
6.3.2. Exkurs: POSIX Threads . . . . . . . . . . . . . . . . . . . .
6.3.3. Exkurs: Netzwerk Programmierung und Cross-Plattform Entwicklung . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3.4. Komponenten . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3.5. Kommunikationsprotokoll . . . . . . . . . . . . . . . . . . .
6.3.6. Softwarearchitektur . . . . . . . . . . . . . . . . . . . . . . .
6.4. Server User-Interface . . . . . . . . . . . . . . . . . . . . . . . . . .
6.4.1. Exkurs: Grafikprogrammierung unter Java . . . . . . . . . .
6.4.2. Komponenten . . . . . . . . . . . . . . . . . . . . . . . . . .
6.4.3. Parser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.5. Server-Architektur-Kommunikation . . . . . . . . . . . . . . . . . .
6.5.1. Nachrichtenorientierte Informationsverarbeitung . . . . . . .
6.5.2. Kommunikationsauf- bzw. -abbau . . . . . . . . . . . . . . .
6.5.3. Start und Terminierung des evolutionären Laufs . . . . . . .
6.6. Zusammenfassung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7. Fahrzeugsimulation
7.1. Konzept . . . . . . . . . . . . . . . . . . . . . .
7.1.1. Ziel . . . . . . . . . . . . . . . . . . . . .
7.1.2. Überlegungen zur Simulation . . . . . .
7.1.3. Arbeitsweise einer Simulation . . . . . .
7.1.4. Manövrierendes Fahrzeug als Modell und
7.1.5. Abbildung der Welt . . . . . . . . . . . .
7.2. Umsetzung . . . . . . . . . . . . . . . . . . . . .
7.2.1. Entwicklungs-Umgebung . . . . . . . . .
7.2.2. Physik des Fahrzeugs . . . . . . . . . . .
7.2.3. Physik des Anhängers . . . . . . . . . .
7.2.4. Die Abbildung der Welt . . . . . . . . .
. . . . .
. . . . .
. . . . .
. . . . .
System
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
47
47
49
49
50
55
55
56
.
.
.
.
.
.
.
.
.
.
.
.
.
57
58
59
60
67
67
70
71
72
72
73
76
76
.
.
.
.
.
.
.
.
.
.
.
79
79
79
79
81
82
83
83
83
84
86
87
VII
Inhaltsverzeichnis
7.2.5. Umsetzung der Simulation . . . . . . . . . . . . . . . . . . . . 89
8. ViewClient
8.1. Konzept . . . . . . . . .
8.2. Netzwerkverbindung und
8.3. 2DView . . . . . . . . .
8.4. 3DView . . . . . . . . .
. . . . . .
-protokoll
. . . . . .
. . . . . .
.
.
.
.
.
.
.
.
9. Pfadfinder
9.1. Algorithmen . . . . . . . . . . . . . . .
9.1.1. Der direkte Weg - Luftlinie . . .
9.1.2. Dijkstra . . . . . . . . . . . . .
9.1.3. A* . . . . . . . . . . . . . . . .
9.1.4. Modifikation für die Simulation
9.2. Umsetzung . . . . . . . . . . . . . . . .
9.3. Vom Pfad zu den Steuerbefehlen . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
97
97
97
99
101
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
103
. 103
. 103
. 103
. 107
. 111
. 116
. 117
10.Wissenserwerb
119
III. Auswertung
121
11.Ergebnisse der evolutionären Testprogramme
11.1. Approximation einer natürlichen Zahl . . . . . . . . .
11.2. Automatische Formelgenerierung, genetische Prognose
11.2.1. Problemstellung . . . . . . . . . . . . . . . . .
11.2.2. Approximation durch Polynome . . . . . . . .
.
.
.
.
123
. 123
. 127
. 127
. 128
.
.
.
.
.
.
.
.
133
. 134
. 135
. 135
. 136
. 142
. 149
. 152
. 154
12.Einparken ohne Anhänger
12.1. Erwartung . . . . . . . . . . . . . . . . . . . . .
12.2. Von der Bewertung zur Fitness . . . . . . . . . .
12.3. Allgemeine Versuchsbedingungen . . . . . . . . .
12.4. Bewertungsfunktion . . . . . . . . . . . . . . . . .
12.5. Bedeutung der Populationsgröße . . . . . . . . . .
12.6. Die Bedeutung der Mutations-Wahrscheinlichkeit
12.7. Die Bedeutung von Eliten . . . . . . . . . . . . .
12.8. Kollision . . . . . . . . . . . . . . . . . . . . . . .
VIII
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Inhaltsverzeichnis
12.9. Abbruchkriterium „Optimum erreicht“
. . . . . . . . . . . . . . . . . 154
13.Einparken mit Anhänger
13.1. Erwartung . . . . . . . . . . . . . . . . . . . . . . .
13.2. Allgemeine Versuchsbedingungen . . . . . . . . . .
13.3. Bewertungsfunktion . . . . . . . . . . . . . . . . . .
13.4. Populationsgröße und Mutations-Wahrscheinlichkeit
13.5. Weitere Bewertungen . . . . . . . . . . . . . . . . .
14.Populationsmodelle
14.1. Einparken ohne Anhänger
14.1.1. Inselmodell . . . .
14.1.2. Netzwerkmodell . .
14.2. Einparken mit Anhänger .
14.2.1. Inselmodell . . . .
14.2.2. Netzwerkmodell . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
15.Ausblick
15.1. Parallelisierung eines genetischen Algorithmus
15.2. Erweiterungen der Server-Software . . . . . .
15.3. Codierung Car . . . . . . . . . . . . . . . . .
15.4. Physiksimulation . . . . . . . . . . . . . . . .
15.5. Fazit . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
157
. 158
. 158
. 158
. 161
. 163
.
.
.
.
.
.
169
. 169
. 169
. 173
. 175
. 176
. 178
.
.
.
.
.
181
. 181
. 183
. 184
. 185
. 185
A. Software Architekturen
187
B. Literaturverzeichnis
195
Erklärung
197
IX
Abbildungsverzeichnis
1.1. Modell der Feinstruktur eines Chromosoms . . . . . . . . . . . . . . .
1.2. Lokale und globale Optima . . . . . . . . . . . . . . . . . . . . . . . .
3.1. Pseudocode eines genetischen Algorithmus
3.2. Beispiele der GA Codierung . . . . . . . .
3.3. Graycode . . . . . . . . . . . . . . . . . .
3.4. Lineare Skalierung . . . . . . . . . . . . .
3.5. Roulette Wheel . . . . . . . . . . . . . . .
3.6. One-Point-Crossover Schema . . . . . . . .
3.7. Two-Point-Crossover Schema . . . . . . . .
3.8. Zufalls-Schablonen Crossing-over . . . . .
3.9. Gleichverteilte Mutation . . . . . . . . . .
3.10. Positions-Mutation . . . . . . . . . . . . .
3.11. Generational Replacement . . . . . . . . .
3.12. Elitismus . . . . . . . . . . . . . . . . . . .
3.13. Schwacher Elitismus . . . . . . . . . . . .
3.14. Delete-n-Last . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
9
22
23
25
28
29
31
32
33
33
34
35
36
36
36
5.1. Kommunen-Modell . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
6.1.
6.2.
6.3.
6.4.
6.5.
6.6.
6.7.
Pakete . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Komponenten der EALib-Bibliothek . . . . . . . . . . . . . . . .
Klassendiagramm des problemunabhängigen Kernels . . . . . . .
Klassendiagramm des Steuerungsmoduls . . . . . . . . . . . . .
Klassendiagramm des problemunabhängigen Bewertungsmoduls
Komponenten des EAServer-Pakets . . . . . . . . . . . . . . . .
Kommunikationsprotokoll der Server-Bibliothek . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
48
49
51
54
55
59
60
XI
Abbildungsverzeichnis
6.8. Arithmetischer Baum . . . . . . . . . . . . . . . . . . . . .
6.9. Arithmetischer Baum: Crossing-Over . . . . . . . . . . . .
6.10. Arithmetischer Baum: Mutation . . . . . . . . . . . . . . .
6.11. Klassendiagram des problemabhängigen Bewertungsmoduls
6.12. Klassendiagramm des Wrappermoduls . . . . . . . . . . .
6.13. Klassendiagramm des Kommunikationsmoduls . . . . . . .
6.14. Komponenten des EAServerUI-Pakets . . . . . . . . . . . .
6.15. Definition der Skriptsprache . . . . . . . . . . . . . . . . .
6.16. Server-Pakete . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
62
63
64
65
66
68
70
72
76
7.1.
7.2.
7.3.
7.4.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
84
85
85
86
9.1. Dijkstra: Ausgangssituation . . . . . . . . . . . . . . . . . . . . . .
9.2. Dijkstra: Start . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.3. Dijkstra: Aktuellen Knoten festlegen und Neue aufnehmen . . . . .
9.4. Dijkstra: Schleifendurchlauf . . . . . . . . . . . . . . . . . . . . . .
9.5. Dijkstra: Zwischenschritte der Wegfindung . . . . . . . . . . . . . .
9.6. Dijkstra: Weg gefunden . . . . . . . . . . . . . . . . . . . . . . . . .
9.7. A*: Ausgangssituation . . . . . . . . . . . . . . . . . . . . . . . . .
9.8. A*: Start . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.9. A*: Aktuellen Knoten festlegen und Neue aufnehmen . . . . . . . .
9.10. A*: Schleifendurchlauf . . . . . . . . . . . . . . . . . . . . . . . . .
9.11. A*: Zwischenschritte der Wegfindung . . . . . . . . . . . . . . . . .
9.12. A*: Weg gefunden . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.13. Modifizierter A*: Situation . . . . . . . . . . . . . . . . . . . . . . .
9.14. Modifizierter A*: Start . . . . . . . . . . . . . . . . . . . . . . . . .
9.15. Modifizierter A*: Aktuellen Knoten festlegen und neue Aufnehmen
9.16. Modifizierter A*: Schleifendurchlauf . . . . . . . . . . . . . . . . . .
9.17. Modifizierter A*: Zwischenschritte der Wegfindung . . . . . . . . .
9.18. Modifizierter A*: Weg gefunden . . . . . . . . . . . . . . . . . . . .
9.19. Modifizierter A*: Komplexer Pfad . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
104
105
105
105
106
107
108
108
109
109
110
111
112
112
113
113
114
114
115
Geradeausfahrt . . . . . . . . . . . . . .
Kurve mit Drehung um den Mittelpunkt
Kurve mit Drehung auf der Hinterachse .
Fahrverhalten mit Anhänger . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
11.1. Fitness-Diagramm: Approximation einer natürlichen Zahl . . . . . . . 127
XII
Abbildungsverzeichnis
11.2. Fitness-Diagramm: Approximation einer Funktion . . . . . . . . . . . 132
12.1. Fitness 1000 . . . . . . . . . . . .
12.2. Fitness 20 bzw. Fitness 40 . . . .
12.3. Beste Fitness der jew. Generation
12.4. Durchschnittliche Fitness der jew.
12.5. Beste Fitness der jew. Generation
12.6. Durchschnittliche Fitness der jew.
. . . . . . .
. . . . . . .
. . . . . . .
Generation
. . . . . . .
Generation
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
140
142
146
146
148
149
13.1. Endposition mit Fitness 20 bei Bewertung 2 . . . . . . . . . . . . . . 164
13.2. Endposition mit Fitness 50 bei Bewertung 3 . . . . . . . . . . . . . . 166
13.3. Endposition mit Fitness 10 bzw. 20 bei Bewertung 4 . . . . . . . . . 167
A.1.
A.2.
A.3.
A.4.
A.5.
A.6.
Klassendiagramm: EALib-Bibliothek . . . . . . . . . . . . .
Klassendiagramm: EAServer-Bibliothek . . . . . . . . . . . .
Auszug aus Klassendiagramm der Benutzeroberfläche . . . .
Nachrichtenorientierte Informationsverarbeitung . . . . . . .
Sequenzdiagramm: Kommunikationsaufbaus und -abbaus . .
Sequenzdiagramm: Start und Terminierung des evolutionären
. . . .
. . . .
. . . .
. . . .
. . . .
Laufs
.
.
.
.
.
.
188
189
190
191
192
193
XIII
Tabellenverzeichnis
4.1. Evolutionsstrategien kontra genetische Algorithmen . . . . . . . . . . 40
6.1. Ereignisobjekte und Handler des evolutionären Servers . . . . . . . . 74
11.1. Algorithmus Parameter: Approximation einer natürlichen
11.2. Ergebnisse: Approximation einer natürlichen Zahl . . . .
11.3. Stützstellen . . . . . . . . . . . . . . . . . . . . . . . . .
11.4. Algorithmus Parameter: Approximation einer Funktion .
11.5. Ergebnisse: Approximation einer Funktion . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
125
126
128
130
131
12.1. Standardkonfiguration . . . . . . . . . . . . . . . . . . . . . . . .
12.2. Testergebnisse bei Standardkonfiguration . . . . . . . . . . . . . .
12.3. Durchschnittliche Zeiten bei unterschiedlichen Populationsgrößen .
12.4. Durchschnittliche Konvergenzzeit bei Populationsgröße 100 . . . .
12.5. Durchschnittliche Konvergenzzeit bei Populationsgröße 200 . . . .
12.6. Durchschnittliche Konvergenzzeit mit Eliten . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
136
141
143
150
150
153
13.1. Standardkonfiguration . . . . . . . .
13.2. Testergebnisse bei Bewertung 2 . . .
13.3. Testergebnisse bei Bewertung 3 . . .
13.4. Testergebnisse bei Bewertung 4 . . .
13.5. Weitere Testergebnisse bei Bewertung
.
.
.
.
4
.
.
.
.
.
.
.
.
.
.
Zahl
. . .
. . .
. . .
. . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
159
164
165
167
168
14.1. Standardkonfiguration . . . . . . . . . . . .
14.2. Zeiten mit Standardmodell . . . . . . . . . .
14.3. Zeiten mit Inselmodell (ohne Anhänger) . .
14.4. Zeiten mit Netzwerkmodell (ohne Anhänger)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
170
171
171
174
XV
Tabellenverzeichnis
14.5. Zeiten
14.6. Zeiten
14.7. Zeiten
14.8. Zeiten
14.9. Zeiten
14.10.Zeiten
bei größeren Populationszahlen (ohne Anhänger)
mit Standardmodell . . . . . . . . . . . . . . . .
mit Inselmodell (mit Anhänger) . . . . . . . . .
mit 10 Inseln und Konvergenzwert 100 . . . . .
mit Netzwerkmodell (mit Anhänger) . . . . . .
bei größeren Populationszahlen(mit Anhänger) .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
175
176
177
178
178
179
15.1. Parallelisierung der evolutionären Prozesse . . . . . . . . . . . . . . . 182
XVI
Vorwort
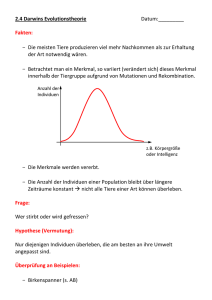
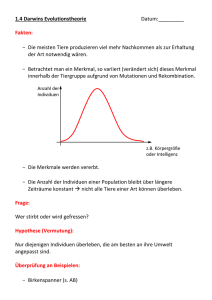
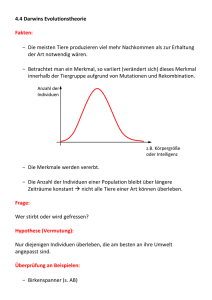
Bisher galt das Einparken im Straßenverkehr als eine Männerdomäne. Dieser Kampf
der Geschlechter um die Fertigkeit des Einparkens kann sich aber bald nivellieren,
denn es wird dann vom Kraftfahrzeug selbst übernommen. Moderne Systeme unterstützen bislang den Fahrer in seiner Fahraufgabe, wie bei der Abstandsregelung
und der Spurhaltung, und entlasten ihn bereits dadurch gezielt. Dennoch ist ein
Fahrzeug noch nicht in der Lage, zum Beispiel eine Parklücke zu erkennen und in
diese seitwärts rückwärts einzuparken. Das in dieser Diplomarbeit entwickelte System soll diese Lücke im Bereich der Fahrerassistenzsysteme schließen. Die hierfür
verwendeten und untersuchten Ideen stammen aus vergangenen Tagen, sind aber
nichtsdestoweniger aktuell. Denn mit dem Streben, die Regeln der Natur zu verstehen, war auch schon immer der Wunsch gegenwärtig, ihre Methoden nutzbringend
für menschliche Kreationen anzuwenden. Dabei steht nicht die exakte Nachbildung
der Arbeitsweise der biologischen Evolution im Vordergrund, sondern die Grundprinzipien der Evolution wie Selektion, Rekombination, Mutation, etc. insoweit zu verstehen und zu modellieren, dass sie auf Computern simuliert und damit zur Lösung
schwieriger theoretischer und praktischer Probleme herangezogen werden können,
bei denen konventionelle Optimierungsverfahren scheitern würden oder aus anderen
Gründen nicht sinnvoll eingesetzt werden können. Diese so genannten evolutionären
Algorithmen finden inzwischen in vielen Bereichen Anwendung, z.B. dem Operation
Research, der Robotik und Künstlichen Intelligenz, der Telekommunikation und Mikroelektronik und bei allgemeinen Optimierungsaufgaben. Neben dieser computergestützten Evolution wird ihre Anwendbarkeit auf ausgewählte Steuerungsprobleme
von Kraftfahrzeugen, u.a. dem Problem des Einparkens aufgezeigt.
Unser Dank gilt Prof. Dr. R. Eck vom Fachbereich Informatik der Georg-Simon-Ohm
Fachhochschule Nürnberg für seine Diskussionsbereitschaft und seinen fachkundigen
Beistand während der Durchführung dieser Diplomarbeit.
Nürnberg, im September 2005
Andreas Blinzler & Andreas Hirschberger
XVII
Projektdefinition
Es wird ein auf evolutionären Verfahren basierendes System entwickelt, welches
u.a. Steuerungsprobleme von Fahrzeugen optimiert und löst. Neben reinen Software Entwicklungsaufgaben sind auch die Analyse der evolutionären Verfahren im
Hinblick auf ihre Einsetzbarkeit, der Methoden des Wissenserwerbs und Computergrafik wichtige Zielpunkte dieser Diplomarbeit.
Eine Grobgliederung des Entwicklungsteils lässt sich wie folgt gestalten: zum einen
in die Erstellung einer Server-Bibliothek zur Kapselung evolutionärer Verfahren und
zum anderen in die Programmierung eines 2-dimensionalen Testbetts, sowie einer
3-dimensionalen finalen Anwendung.
Bei der Programmierung der Bibliothek zur Kapselung der evolutionären Verfahren
soll auf Effizienz und Erweiterbarkeit geachtet werden. Sie wird in ihrem Aufbau so
geschaffen sein, dass ohne weiteres Zutun nachfolgender Software Entwickler neue
evolutionäre Strategien1 hinzugefügt werden können, jedoch unter Beachtung der
Tatsache, dass der evolutionäre Prozess in der Reihenfolge Bewertung, Skalierung,
Kreieren der nächsten Generation vollzogen wird. Die effiziente Programmiermethotik ist in der Weise zu finden, dass stets versucht wird die effizienteste Codierung
für die Beschreibung des zu optimierenden Problems zu wählen. Jedoch muss auch
hier unter Berücksichtigung der Tatsache moderner leistungsstarker Computer die
mögliche Speichereffizienz mit der einfachen Handhabung der Codierung für die evolutionären Verfahren abgewägt werden. Ebenfalls wird keine interpretierte sondern
kompilierte Sprache (C++) zur Realisierung verwendet. Des Weiteren soll diese mit
einer Benutzerschnittstelle zur vereinfachten Bedienung versehenen werden. Aufgrund der an das System gestellten Anforderung der Portabilität wird diese in der
Sprache Java unter zu Hilfenahme des Swing Frameworks erstellt. Diese Entscheidung fordert die Programmierung eines Wrappers, welcher die Aufgabe der Vermittlung zwischen den beiden Sprachen C++ (Bibliothek) und Java (GUI) übernimmt.
Die Bibliothek zur Kapselung der evolutionären Verfahren soll lediglich alle pro1
Selektion, Heiratsschema, Ersetzungsschema, Genome, usw.
XIX
Projektdefinition
blemunabhängigen Teile des Algorithmus enthalten. Problemabhängige Methoden2
werden zusammen mit dem Wrapper und einer Komponente zur Kommunikation
zu einer Server-Bibliothek zusammengefasst. Diese wird über ihre KommunikationsKomponente die Anbindung von verschiedenen Clients realisieren, unabhängig von
der zugrunde liegenden Technologie. Bibliothek, Server und Benutzerschnittstelle
werden zusammen eine serverseitige Anwendung bilden, welche es verschiedenen
Client-Anwendungen ermöglichen wird ihre evolutionären Verfahren zu nutzen.
Neben der Erstellung verschiedener solcher Client-Anwendungen wird die Entwicklung einer Applikation zur Simulation von Fahrzeugen ein wichtiger Projektpunkt
sein. Mit dieser soll die Einsetzbarkeit evolutionärer Verfahren zur Lösung komplexer Aufgaben im Bereich der Fahrzeugsteuerung analysiert werden. Hierfür wird
das Verhalten eines Fahrzeugs bei niedrigen Geschwindigkeiten vereinfacht abgebildet. Die Visualisierung der simulierten Welt übernimmt ein über TCP verbundener
View-Client; es wird ein 2-dimensionaler, sowie 3-dimensionaler Client entwickelt.
Die Entwicklung der Simulation und Darstellung wird unter Verwendung des .NETFrameworks in C# erfolgen. Der 2D-Client soll die C#-Grafikroutinen verwenden,
während der 3D-Client auf DirectX basieren wird.
Bei der Entwicklung der Simulation soll ebenfalls auf Erweiterbarkeit, sowohl der
simulierten Welt als auch der Fahrzeugsteuerung, geachtet werden. Erweiterte Steuerungsaufgaben sollen ohne großen Aufwand eingearbeitet werden können. Für die
Schaffung realistischer Szenarien wird sich das Fahrzeug frei durch die simulierte
Welt bewegen können. Szenarien werden über Konsolenbefehle oder durch festgelegte Situationen angestoßen, woraufhin das selbstständige Lernen beginnen wird.
Ist für ein bestimmtes Szenario eine Lösung erarbeitet, soll diese gespeichert und für
das erneute Auftreten dieses Szenarios genutzt werden. Auch diese Lernkomponente
soll austauschbar gehalten werden. Es wird möglich sein, eine alternative, externe
Anwendung zu starten und diese über Netzwerk mit der Simulation zu verbinden.
Die Szenarien, deren Lösbarkeit getestet werden sollen, umfassen das Einparken eines Fahrzeugs rückwärts-seitwärts, mit und ohne Anhänger. Weitere Probleme, wie
z.B. ein Wendemanöver auf einer Spur oder das Rückwärtsfahren mit Anhänger
werden ebenfalls untersucht. Die Ergebnisse sollen Vor- und Nachteile des Einsatzes
evolutionärer Verfahren, sowie die Unterschiede zwischen verschiedenen Methoden
und Codierungen aufzeigen.
2
Codierung, Bewertung, Crossing-over, Mutation
XX
Teil I.
Theorie
1
1. Evolution und Genetik
Charles Darwins Buch von 1859 On the Origin of Species by means of Natural Selection, or the Preservation of Favoured Races in the Struggle of Life ist das erste
Werk, das die damaligen Theorien und Hypothesen zur Evolution der Lebewesen
zusammenfasst und durch eine Fülle von Beobachtungen belegt: Evolutionstheorie,
Gradualismus, Deszendenztheorie, Speziation. Die besondere Leistung von Darwin
liegt in der Erklärung des Evolutionsmechanismus durch das heute noch immer gültige Prinzip der wechselseitigen Beziehung zwischen Variation und Selektion. Jedoch
erkannte und beschrieb erst der Botaniker Gregor Johann Mendel wichtige Gesetzmäßigkeiten, die sich hinter diesem Prozess verbergen. Mendel entdeckte um das
Jahr 1865 die ihm benannten Vererbungsgesetzte. Das Uniformitätsgesetz besagt,
dass bei der Kreuzung zweier reinerbiger Vorfahren (Parentalgeneration), die sich in
einem oder mehreren Merkmalen unterscheiden, nur einheitlich (uniform) aussehende Nachkommen in der ersten Nachfolgegeneration (Filialgeneration) auftreten. Das
Spaltungsgesetz besagt, dass bei einer Kreuzung der ersten Filialgeneration untereinander in der zweiten Filialgeneration eine Aufspaltung der Merkmalsausprägungen
auftritt. Sie weisen somit kein uniformes Erscheinungsbild mehr auf. Die Anzahl der
Individuen mit bestimmten Merkmalsausprägungen ist davon abhängig, ob die sich
unterscheidenden Erbmerkmale in der Parentalgeneration dominant oder rezessiv
waren. Aus diesen Erkenntnissen resultieren der dominant-rezessive und intermediäre Erbgang. Der Unterschied liegt im Aufspaltungsverhältnis der Individuen in der
zweiten Filialgeneration. Das Rekombinationsgesetz besagt, dass sich bei mehreren
Unterscheidungsmerkmalen in der Parentalgeneration die einzelnen Merkmalspaare
in der zweiten Filialgeneration unabhängig voneinander aufspalten und frei miteinander rekombiniert werden können. Die Mendelschen Gesetzte stellen die Grundlage der modernen Molekulargenetik dar, welche wiederum ihrerseits Anreize der
Informatik bietet, um ihre Mechanismen nutzbringend für die Lösung komplexer
Aufgaben einzusetzen.
3
1 Evolution und Genetik
1.1. Molekular- und Evolutionsgenetik
Die Molekular- und Evolutionsgenetik ist für das Verständnis der Vererbungsvorgänge und der Mechanismen der Evolution von zentraler Bedeutung. Im Folgenden
werden die wichtigsten genetischen Begriffe und Mechanismen näher erläutert.
1.1.1. Chromosom
Ein Chromosom ist die Organisationsstruktur der Desoxyribonukleinsäure (DNS) mancher eukaryotischer Organismen1 und befindet
sich in deren Zellkernen. Ein Chromosom ist ein langer Strang, der
um eine Vielzahl von Histonen (Kernproteinen) herumgewickelt und
mehrfach zu einer kompakten Form
spiralisiert werden kann. Die Chromosomen wurden 1842 von Carl Abbildung 1.1.: Modell der Feinstruktur eines
Wilhelm von Nägeli entdeckt, jeChromosoms
doch als transitorische Zytoblasten2 mißgedeutet. 1910 zeigte Thomas Hunt Morgan, dass die Chromosomen die
Träger der Gene, der Erbinformation, sind.
1.1.2. Zellteilung
Die Zellteilung ist der biologische Prozess, der das Wachstum und die Fortpflanzung aller Lebewesen gewährleistet. Bei der Zellteilung entstehen zwei neue Zellen
aus einer alten. Im Normalfall, bei der Mitose der Eukaryoten, ist nach der Teilung das Erbgut der Tochterzellen identisch mit dem der Elternzelle. Eine zweite
Form der Teilung, die Meiose, führt zur Bildung von Keimzellen, die der geschlechtlichen Fortpflanzung dienen. Während der Meiose kommt es zu einer Reduzierung
des Chromosomensatzes, d.h. die Zellen sind nach vollzogener Teilung nicht mehr
1
2
4
Als Eukaryoten oder Eukaryonten werden alle Lebewesen mit Zellkern zusammengefasst
Zellkern
1.1 Molekular- und Evolutionsgenetik
diploid3 wie ihre Vorläuferzellen, sondern haploid4 . Wenn in einem Organismus die
Zellteilung unkontrolliert abläuft, spricht man von Wucherungen, Geschwüren oder
Tumoren. Krebs ist eine der gravierensten Störungen dieser Art.
1.1.3. Genetische Information
Die Chromosomen sind die Träger der Erbinformation, der Gene. Die Chromosomen
bestehen aus Nukleinsäuren und Proteinen. Der wichtigste chemische Bestandteil
der Chromosomen ist die DNS. Sie ist ein Makromolekül, das in der Vererbung als
Träger der Information dient. Anhand dieser Information, die in einer bestimmten
Form in die DNS eingeschrieben ist (dem genetischen Code), werden Proteine produziert. Das Makromolekül ist aus den chemischen Elementen Kohlenstoff, Wasserstoff,
Sauerstoff, Phosphor und Stickstoff zusammengesetzt. Die Struktur der DNS wurde
1953 von James Watson und Francis Crick aufgeklärt, die 1962 dafür mit Maurice
Wilkins den Nobelpreis für Medizin erhielten.
Nach dem Modell von Watson und Crick ist die DNS insgesamt aus zwei gegenläufigen DNS-Einzelsträngen aufgebaut. Die DNS besitzt eine Strickleiter-Struktur, bei
der die zwei Holme der Leiter um eine gedachte Achse schraubenförmig gewunden
sind (Doppelhelixstruktur ). Die beiden Holme der Strickleiter werden aus Hunderttausenden sich abwechselnden Desoxyribose- und Phosphat-Bausteine gebildet. Die
Sprossen bestehen aus je zwei organischen Basen (Basenpaar), die über Wasserstoffbrücken5 miteinander verbunden sind und dafür sorgen, dass die beiden Holme auch
im schraubenförmigen Zustand der Strickleiter verknüpft bleiben und im gleichen
Abstand nebeneinander liegen. Insgesamt gibt es in der DNS vier verschiedene organische Basen: Adenin, Thymin, Guanin und Cytosin (vgl. Abbildung 1.1).
Die in der DNS vorliegenden Basenpaare werden von den jeweils komplementären
Basen Adenin und Thymin, sowie Guanin und Cytosin gebildet. Das Makromolekül
DNS ist demzufolge aus einer Vielzahl von vier verschiedenen Nukleotiden6 zusammengesteckt. Jeweils drei solcher Basen bilden ein so genanntes Basentriplett.
3
Jedes Chromosom liegt in doppelter Anzahl vor
Der Zellkern enthält von allen verschiedenen Chromosomen nur ein Exemplar
5
Sind chemische Bindungen, welche entstehen, wenn zwei Moleküle über ihre Wasserstoffatome
in Wechselwirkung treten
6
Nukleotid = Base + Zucker mit 5 C-Atomen + Phosphorsäure
4
5
1 Evolution und Genetik
Genetischer Code
Der genetische Code ist eine Anleitung, nach der Nukleotidtripletts (Codons) während der Protein-Biosynthese in Aminosäuren übersetzt werden. Vor diesem Prozess
wird der DNS-Abschnitt eines Gens zunächst in ein Messenger-Ribonukleinsäure
(mRNS) Molekül umgeschrieben (Transkription); danach können bestimmte Teile
dieser mRNS gezielt entfernt werden (Spleißen). Während der Translation, werden
die zu den Codons passenden Aminosäuren miteinander zu einer Polypeptidkette7
verknüpft. Einige Codons stehen nicht für eine Aminosäure, sondern werden als
Stopp-Zeichen behandelt, welches die Translation beendet (Stopp-Codons).
Es existieren maximal 43 = 64 Codons zur Beschreibung von Aminosäuren. Von
diesen kodieren lediglich drei keine Aminosäuren (Stopp-Codons).
Des Weiteren ist der genetische Code redundant ausgelegt; die Aminosäuren werden
in der Regel durch mehrere Tripletts kodiert8 . Ebenfalls ist der genetische Code in
der Natur universell gültig, d.h. alle Organismen übersetzen die Basensequenzen in
der gleichen Art und Weise.
1.1.4. Gen
Ein Gen ist ein Abschnitt auf der DNS, der die Beschreibung der AminosäureSequenz eines Proteins enthält (genetischer Code). Dieses Protein prägt durch seine
Funktion ein Merkmal. Folglich ist ein Gen eine Erbanlage, ein Träger von Erbinformation, der durch Reproduktion an die Nachkommen weitergegeben werden kann.
Gene sind fähig zu mutieren. Diese spontanen oder durch Einwirkung von außen
herbeigeführten Veränderungen können an verschiedenen Stellen im Gen erfolgen.
Demzufolge kann ein Gen nach einer Reihe von Mutationen in verschiedenen Zustandsformen vorliegen (Allele).
Bei allen Lebewesen kodiert nur ein Teil der DNS Proteine. Die übrigen Teile sind
für die Genregulation notwendig, oder bei höheren Lebewesen, für die Architektur
der Chromosomen wichtig. Bei eukaryotischen Genen wird zwischen Protein kodierenden Exons und nicht kodierenden Introns unterschieden.
7
8
6
organische chemische Verbindung aus einer Verknüpfung mehrerer Aminosäuren
Die Aminosäure Alanin wird durch die Tripletts: GCU, GCC, GCA und GCG kodiert.
1.2 Evolutionsfaktoren und die Mechanismen der Evolution
1.2. Evolutionsfaktoren und die Mechanismen der
Evolution
Zur Programmierung von evolutionären Algorithmen genügt der bisherige Überblick
noch nicht ganz. Es müssen noch einige Begriffe genauer erläutert werden, um zu
verdeutlichen in welcher Weise sich die Mechanismen und Faktoren der Evolution
auswirken.
1.2.1. Zufall
Der Zufall spielt in vielen Bereichen der Evolution eine entscheidende Rolle. Die
Zellteilung, die sexuelle Rekombination, die Auswahl der Geschlechtszellen, das
Crossing-over und viele andere Prozesse unterliegen dem Einfluss von Zufallsfaktoren. Repräsentativ seien zwei näher beschrieben:
1. Mutationen sind zufällig, da nicht vorhergesagt werden kann, an welchem Genort und mit welchem Effekt sie auftreten werden. Die spontane Mutationsrate
lässt sich zwar durch bestimmte Einwirkungen erhöhen, die Auswirkungen erhöhter Mutationen unterliegen aber wieder dem Zufall.
2. Obwohl die Wahrscheinlichkeit für ein Crossing-over an jeder Stelle des Chromosoms nicht gleich groß ist, kann der Kreuzungspunkt dennoch an jeder beliebigen Stelle des Chromosoms liegen. Die Rekombination der Gene unterliegt
damit ebenfalls dem Zufall.
1.2.2. Evolution von Populationen
Bewegt man sich vom Standpunkt der Molekulargenetik weg und betrachtet die
Evolution aus Sicht der Populationen, so treten die oben beschriebenen molekulargenetischen Fakten in den Hintergrund. Im Mittelpunkt stehen die Betrachtungen
von Populationsschwankungen und deren Auswirkungen auf die Evolution.
In einer kleinen Population kommt in der Regel nur ein geringer Teil der Nachkommen zur Fortpflanzung, so dass die Wahrscheinlichkeit einer durchgängigen Rekombination der Gene des Genpools sinkt. Je kleiner folglich eine Population ist, desto
geringer wird ihre genotypische9 Varianz. Die Population driftet somit in Richtung
9
Der Genotyp eines Organismus repräsentiert seinen Individuellen Satz von Genen im Zellkern.
Der Phänotyp ist die Summe aller äußerlich feststellbaren Merkmale eines Individuums.
7
1 Evolution und Genetik
Gleichförmigkeit ab, bis keine Varianz der Individuen mehr existiert.
Ein ähnlicher Effekt tritt bei Populationen auf, die sich aufspalten und voneinander
isolieren. Die einzelnen Populationsteile werden in sich gleichartig, entwickeln sich
als Populationen jedoch durch Gendrift und Genverlust auseinander.
In einer großen, ursprünglich uneinheitlichen Population herrscht ein starker Mutationsdruck. Es sind vielfältige Rekombinationen des Genbestandes möglich. Sie
tendieren daher im Gegensatz zu kleinen Populationen zu einer Ungleichförmigkeit des Erbgutes. Durch den Selektionsdruck und den Selektionsvorteil bestimmter
Genotypen kann dennoch eine Gleichförmigkeit der Erbanlagen entstehen. Folglich
wirkt der Selektionsdruck vereinheitlichend, der Mutationsdruck diversifizierend.
1.2.3. Populationswellen
Populationen können starken Schwankungen unterliegen. Sie können als Ganze oder
zu großen Teilen zugrunde gehen. Es ist jedoch auch möglich, dass es zu Populationswellen kommt, in denen sich die Individuen explosionsartig vermehren. Ursachen
hierfür sind häufig Umweltbedingungen. Diese Wellen können in einer Aufspaltung
der Populationen in geographisch getrennte Areale resultieren. Einnischungen sind
bei dieser Entwicklung ein häufig beobachteter Seiteneffekt.
In natürlichen Populationen ist trotz der häufig festzustellenden Bestandsschwankungen bei vielen Arten ein gegenläufiger Trend zu beobachten: die Populationsgröße strebt einen konstanten Wert zu. Dies gründet in der Tatsache, dass die meisten
Arten in ihrer natürlichen Umwelt Feinde haben, welche dafür Sorge tragen, dass
sich ihr Bestand nicht beliebig vergrößert. Darüber hinaus ergeben sich aus den verfügbaren Nahrungsquellen und Umweltfaktoren Schranken für einen ungehinderten
Bestandszuwachs.
1.3. Evolution als Optimierungsprozess
Aus der Sicht eines Informatikers stellt die Evolution ein Optimierungsverfahren
dar, welches durch Manipulation der Erbinformation und die damit verbundenen
grundlegenden Steuerungsmechanismen in der Lage ist, komplexe Organismen und
Lebensformen in relativ kurzen Zeiträumen an ihre Umwelt- und Lebensbedingungen
anzupassen; die Evolution ein Suchprozess im Raum der genetischen Informationen
bzw. im Raum der möglichen Erbanlagen. Ihr Ziel ist das Auffinden der Erbanlagen,
8
1.3 Evolution als Optimierungsprozess
die ein Individuum oder eine Art am Besten dazu befähigen, sich im survival of the
fittest zu bewähren. Nach Rechenberg lässt sich dieser Suchraum, den die Evolution
zur Adaption der Individuen nach optimalen Lösungen durchsuchen muss, durch
einen diskreten Raum beschrieben. Die Gitterpunkte dieses Raumes stehen für alle
möglichen Kombinationen von Nukleotidbasen, die im menschlichen Chromosom
vorkommen können (nach Rechenberg ca. 3 ∗ 109 ).
Prinzipiell beruht der evolutionäre Suchprozess auf drei Mechanismen: der Mutation
der genetischen Information, der Rekombination der Erbinformation (Crossing-over)
und der Selektion aufgrund der Tauglichkeit eines Individuums.
Abbildung 1.2.: Lokale und globale Optima
1.3.1. Evolution als kombinierte Suchstrategie
Die Evolution kombiniert ungerichtete Suchprozesse mit Gerichteten. Mutationen
des Erbgutes bewirken die Erzeugung von Varianten und Alternativen. Aus der
Sicht der Optimierungstheorie kommt der Mutation folglich die Aufgabe zu, lokale
Optima10 zu überwinden. Damit wird ein Einpendeln der evolutionären Suche bei
suboptimalen Lösungen verhindert.
Rekombinationen (Crossing-over) bewirken ein zufälliges Mischen des Erbgutes, folgen aber statistischen Gesetzen (vgl. Mendelsche Gesetze, Kapitel 1).
Die Selektion hingegen führt die eigentliche Steuerung der Evolution durch. Indem
sie festlegt, welche Phänotypen sich stärker vermehren als andere, bestimmt sie
10
vgl. Abbildung 1.2
9
1 Evolution und Genetik
die Richtung, in die sich das Erbgut verändert. Gäbe es keine Störungen, so wäre
die Selektion eine deterministische Komponente; sie würde den Lauf der Evolution
festlegen. Zufällige Ereignisse11 machen sie aber zu einem nicht deterministischen
Faktor.
Es wird durch die Betrachtungsweise der Evolution als Suchprozess deutlich, weshalb
die Natur mannigfaltige Individuen beherbergt. Ein Genpool wird an sich verändernde Lebensbedingungen im Lauf der Zeit angepasst. Für eine effiziente Optimierungsstrategie gäbe es folglich im wesentlichen nur zwei Alternativen: entweder die
Generationsfolgen sehr kurz halten, um Individuen in der Generationsfolge an sich
verändernde Bedingungen schnell anzupassen, oder die gleichzeitige Erzeugung vieler Individuen, um auf diese Weise die benötigte Evolutionszeit zu minimieren. Die
Evolution verfolgt eine Kombination dieser beiden Strategien. Die bei fast allen Arten unterschiedliche Kombination von Reproduktionszeit und Reproduktionsquote
bewirkt aus der Sicht klassischer Suchstrategien eine gekoppelte Tiefen- und Breitensuche. Leben zur gleichen Zeit mehrere Individuen derselben Gattung, werden
diese simultan auf ihre Tauglichkeit getestet. Damit gelingt es der Evolution den
hochdimensionalen Suchraum der genetischen Information simultan von mehreren
Punkten (Genotypen) aus zu durchsuchen. Diese Parallelität resultiert in einem Zeitvorteil, welcher die Wahrscheinlichkeit optimale Punkte zu erreichen erhöht und die
Wahrscheinlichkeit suboptimale Pfade zu verfolgen reduziert.
1.3.2. Globale und lokale Optima
Das Ziel der Evolution ist das systematische Finden optimaler Parameterwerte. Gegeben seien reelle (Parameter-) Vektoren
x ∈ M = M1 × M 2 × . . . × M n
(1.1)
und eine Zielfunktion z, die jedem solchen Vektor eindeutig einen (Qualitäts- oder
Güte-) Wert zuordnet.
z : M = M1 × M2 × . . . × Mn → <, M 6= 0
(1.2)
Aufgabe bei einem Optimierungsproblem ist es, einen Vektor x∗ ∈ M von Parametern zu finden, so dass gilt:
∀x ∈ M : z(x) ≥ z(x∗ )
11
(1.3)
Umwelt und Lebensverhältnisse, die Rückkopplung der Individuen mit ihrer Umwelt, die Selektion ist keine konstante Größe
10
1.4 Konventionelle Optimierungsverfahren
Folgt ein x∗ dieser Bedingung beschreibt es ein globales Minimum (vgl. Abbildung
1.2).
Neben den globalen Minima existieren in der Regel so genannte lokale Minima. Ein
lokales Minimum xlok ist definiert:
∃e | ∀x : |x − xlok | < e ⇒ z(xlok ) ≤ z(x)
(1.4)
Im Gegensatz zu einem globalen Minimum stellt folglich ein lokales Minimum nur
innerhalb eines bestimmtes Intervalls einen Extremwert dar. Außerhalb dieses Bereichs können noch weitere kleinere Werte der Zielfunktion zu finden sein.
Die hier durchgeführte Beschränkung auf die Behandlung von Minimierungsproblemen stellt keine Einschränkung dar, denn Maximierungsprobleme können auf
Minimierungsprobleme zurückgeführt werden (und umgekehrt):
maximum{z(x)|x ∈ M } = −minimum{−z(x)|x ∈ M }
(1.5)
Die Zielfunktion z wird bei der Simulation der Evolution meist als Qualitäts- oder
Bewertungsfunktion bezeichnet. Mittels genetischer Algorithmen und Evolutionsstrategien (vgl. Kapitel 3 und 2) werden effiziente Parametervektoren gesucht, bei
denen die Qualitäts-/Bewertungsfunktion einen optimalen Wert12 annimmt.
1.4. Konventionelle Optimierungsverfahren
Die klassischen Optimierungsverfahren lassen sich grob in deterministische und nicht
deterministische Verfahren untergliedern.
1.4.1. Deterministische Verfahren
Die bekanntesten Verfahren dieser Klasse sind u.a. die Gauß-Seidel Strategie, die
Gradienten Strategie und das Simplex-Verfahren. Sie können unter Hill-Climbing
Verfahren zusammengefasst werden, da sie im Prinzip wie ein Bergsteiger, immer
an dem lokalen Anstieg orientiert sind und sich bevorzugt dorthin bewegen, wo ein
Anstieg festzustellen ist. Zur Erläuterung der Verfahren wird ein n-dimensionaler
Parameterraum mit den Parametern < p1 , p2 , . . . , pn > angenommen.
12
Ein globales Optimum würde den gesuchten Vektor definieren; ein lokales Optimum repräsentiert
eine suboptimale Lösung des Problems
11
1 Evolution und Genetik
Gauß-Seidel Strategie
Bei der Gauß-Seidel Strategie wird der Parameter p1 in eine Richtung verändert.
Steigt die Qualitätsfunktion Q, so wird der Parameter weiter in diese Richtung
verändert, bis der maximal zulässige Wert für p1 erreicht ist oder bis der Wert
der Qualitätsfunktion kleiner wird. In diesem Fall wird der nächste Parameter p2
verändert. Fällt der Wert von Q nach dem ersten Schritt der Veränderung von p2 , so
wird wie oben beschrieben, allerdings in entgegengesetzter Richtung weiterverfahren.
Diese Prozedur wird so lange fortgesetzt, bis alle Parameter angepasst wurden und
beginnt dann von neuem, bis ein zufrieden stellender Wert für Q erreicht wurde.
Gradienten Strategie
Die Gradienten Strategie richtet sich in jedem Punkt des n-dimensionalen Qualitätsgebirges nach dem steilsten Tangentenanstieg. Hierfür wird die partielle Ableitung
der Qualitätsfunktion nach den Parametern bestimmt. Die Parameteranpassung erfolgt in Richtung des steilsten Gradienten und proportional zur Steigung, d.h. in
der Nähe des Optimums erfolgen kleine Adaptionsschritte, in weiterer Entfernung
größere.
Simplex Verfahren
Das Simplex Verfahren arbeitet nach einem anderen Prinzip. Es ähnelt den evolutionären Algorithmen darin, dass nicht von einem Startpunkt (einem speziellen
Parametervektor) begonnen wird, sondern von mehreren gleichzeitig. Anstelle eines
Startpunkts werden im n-dimensionalen Raum n+1 Startpunkte verwendet. Sie werden so gesetzt, dass sie untereinander gleiche Abstände haben. Im 2-dimensionalen
Raum ergibt dies ein gleichseitiges Dreieck, im 3-dimensionalen einen Tetraeder und
im n-dimensionalen Raum ein regulären Polyeder (Simplex ). Im ersten Schritt nach
der Festlegung der Startpunkte werden diese bewertet.
Der Eckpunkt des Simplex mit dem schlechtesten Wert wird gestrichen. An seine
Stelle tritt ein neuer Punkt, der durch Spiegelung des gelöschten Punktes am Mittelpunkt des verbleibenden n-Ecks hervorgeht. Durch dieses Vorgehen kann es zu
Oszillationen kommen, da der neue Punkt ebenfalls der schlechteste sein kann, was
dazu führen würde, dass der gerade gestrichene Punkt wieder erzeugt werden würde.
Um solche Oszillationen zu verhindern, wählt man in diesem Fall den zweitschlechtesten Punkt für die Spiegelung. Nach einigen Iterationen werden nur noch Polyeder
12
1.4 Konventionelle Optimierungsverfahren
gebildet, die um den Eckpunkt mit dem höchsten Qualitätswert rotieren. In diesem
Stadium kann nur noch eine Qualitätsverbesserung durch Verkürzung der Kantenlänge der Polyeder erreicht werden.
1.4.2. Nicht deterministische Verfahren
Die Grundidee nicht deterministischer Optimierungsverfahren besteht im Weggang
von deterministischen Vorschriften hin zum systematischen Gebrauch des Zufalls.
Wenn über die Lage der Optima in einem großen Suchraum keine Kenntnisse vorhanden sind, sind zufallsgesteuerte Verfahren effizienter als deterministische Algorithmen. Die Gefahr, Optima nicht zu finden ist beispielsweise bei einer gleichmäßigen
Streuung der Zufallsstichproben im Suchraum relativ gering. Diese Gefahr besteht
aber bei einer deterministischen Suche, wenn durch die Systematik die optimalen
Werte nicht gefunden werden können. Dies ist der Fall, wenn das Verfahren auf einer geringfügig falschen Annahme basiert. Für Fälle in denen man keine Kenntnis
über die Optima im Suchraum besitzt, ist folglich eine systematische, zufallsbasierte
Suche zuverlässiger. Das einfachste zufallsbasierende Verfahren ist das Monte-Carlo
Verfahren.
13
2. Evolutionsstrategien
Die Informatik kennt im Wesentlichen zwei Modelle der Evolution für Computersimulationen und Anwendungen: die in diesem Kapitel zu erläuternden Evolutionsstrategien und die genetischen Algorithmen (vgl. Kapitel 3).
Die Frage nach der geeignetsten Repräsentation oder Modellierung der relevanten
Details spaltete die Evolutionstheoretiker in zwei Lager. Auf der einen Seite steht
die deutsche Schule der Evolutionsstrategen um I. Rechenberg, welche die biologische
Evolution als Richtschnur verwendet. Auf der anderen Seite steht die amerikanische
Schule der genetischen Algorithmen um J. Holland und D. Goldberg, die sich stärker
für die Frage interessieren, wie es der Evolution gelingt, Informationen zu codieren
und über die Generationen weiterzureichen.
2.1. Codierung
Aus der Sicht der Evolutionsstrategen lässt sich die relevante Erbinformation eines
Individuums in Vektoren von reellen Zahlen codieren; die Individuen einer Population werden von diesen Vektoren repräsentiert. Eine Population von Individuen
ist folglich eine Menge solcher Vektoren. Dieser Ansatz hat historische Gründe: I.
Rechenberg war als Ingenieur zusammen mit seinen Mitarbeitern an der Lösung
von Problemen der Reellen-Optimierung interessiert. Er wollte technische Probleme lösen, indem er die Evolution und ihre Mechanismen als Vorbild nahm. Seine
Forschung konzentrierte sich daher jahrelang auf Probleme, bei denen das Finden
optimaler Systemparameter das größte Problem darstellte.
Eine Repräsentation von Optimierungsproblemen durch reelwertige Vektoren stellt
die kompakteste Form einer Codierung dar. Allerdings ist sie immer von der jeweiligen Aufgabenstellung abhängig. Es existiert keine Problem-invariante optimale
Codierung. Bei diskreten Optimierungsaufgaben oder bei der Suche nach optimalen
Strukturen sind binäre Codierungen nahe liegender.
15
2 Evolutionsstrategien
2.2. Varianten
2.2.1. (1+1) - Evolutionsstrategie
Die einfachste Form der Evolutionsstrategien ist die so genannte (1+1) - Evolutionsstrategie. Ausgehend von einem Ur-Individuum/Elter (einem Vektor reeller Zahlen),
wird ein zweites Individuum/Nachkomme (ein zweiter Vektor) erzeugt, indem der
Ausgangsvektor zunächst dupliziert wird. Dieser Vorgang simuliert nach Rechenberg den Prozess der DNS-Selbstverdopplung. In einem zweiten Schritt wird das
Duplikat zufällig modifiziert. Die Mutation wirkt wie folgt: auf jedem Parameter
des Vektors wird ein zufälliger (in der Regel kleiner) positiver oder negativer Wert
addiert. Im nächsten Schritt werden der Ausgangsvektor und das mutierte Duplikat bewertet. Hier kommt es zu einem survival of the fittest: der Vektor, dem die
Bewertungsfunktion den besseren Wert zuordnet, überlebt und wird zur Erzeugung
neuer Nachkommen nach dem gleichen Schema herangezogen. Der schlechtere von
beiden wird nicht weiter berücksichtigt. Haben beide den gleichen Wert durch die
Bewertungsfunktion erhalten, so wird zufällig einer von beiden ausgewählt.
Das Verfahren wird so lange vollzogen bis die Qualität eines Nachkommen hinreichend gut ist1 . Diese Evolutionsstrategie ist ein serieller Prozess; es existieren keine
Populationen, sondern lediglich zwei Individuen zur gleichen Zeit.
2.2.2. (µ+λ) - Evolutionsstrategie
Die (µ+λ) - Evolutionsstrategie stellt eine Verallgemeinerung der oben beschriebenen (1+1) - Evolutionsstrategie dar. Sie dient dem Zweck deren seriellen Charakter
zu überwinden. An die Stelle eines Elters treten µ Eltern und λ Nachkommen (mit
λ≥µ≥1). Die Evolutionsschritte der (µ+λ) - Evolutionsstrategie entsprechen denen
der (1+1) - Evolutionsstrategie. Aus µ Eltern werden λ Eltern für die Erzeugung
von λ Nachkommen (Duplikate) zufällig ausgewählt. Die Auswahl trifft mit gleicher
Wahrscheinlichkeit jedes Individuum der Elternpopulation. Eine Mehrfachauswahl
eines Elters ist zulässig. Die λ Duplikate werden mutiert und zusammen mit den
Eltern bewertet. Die µ besten Individuen repräsentieren die Eltern der nächsten
Generation. Die Größe der Elternpopulation bleibt somit konstant µ.
1
Abhängig von der Problemstellung muss eine Lösung gefunden oder approximiert werden
16
2.2 Varianten
2.2.3. (µ,λ) - Evolutionsstrategie
Bei der (µ+λ) - Evolutionsstrategie werden Eltern und Nachkommen einer Generation gemeinsam bewertet. Dies hat zur Folge, dass überdurchschnittlich gute Individuen, viele Generationen überleben. Dieser Effekt kann zu einer vorzeitigen Konvergenz
des Evolutionslaufs gegen ein lokales Optimum führen.
Daher modelliert die (µ,λ) - Evolutionsstrategie die biologische Evolution naturgetreuer als die (µ+λ) - Evolutionsstrategie: jedes Individuum lebt nur noch für die
Dauer einer Generation.
Das Verhindern einer vorzeitigen Konvergenz hat jedoch auch Nachteile. Die Bewertungsfunktion unterliegt bei der (µ,λ) - Evolutionsstrategie starken Schwankungen
und ist in der Regel nicht monoton.
2.2.4. (µ#λ) - Evolutionsstrategie
Die (µ#λ) - Evolutionsstrategie erlaubt eine Beschreibung und Simulation des Selektionsdrucks innerhalb einer Population als auch von Populationswellen. Der Selektionsdruck wird aus den Quotienten s = (µ/λ) gebildet: je kleiner der Quotient
ist, desto stärker ist der Selektionsdruck innerhalb einer Population. Durch eine
geeignete Wahl der Parameter µ und λ kann der Selektionsdruck zwischen den Extremwerten 1 (geringer Selektionsdruck) und 0 (starker Selektionsdruck) beliebig
genau eingestellt werden.
Nach dem gleichen Schema lassen sich ebenfalls Populationswellen simulieren. Der
Parameter µ wird systematisch oder zufallsgesteuert verändert. Bei Populationswellen mit gleich bleibenden Selektionsdruck müssen die Werte von µ und λ im
gleichen Verhältnis verändern werden. Bei Populationswellen mit sich verändernden
Selektionsdruck genügt es einen der Parameter konstant zu halten.
2.2.5. (µ/ρ#λ) - Evolutionsstrategie
Die bisher vorgestellten Varianten der Evolutionsstrategien machen keinen Gebrauch
von der sexuellen Rekombination. Das Erzeugen der λ Duplikate wird in dieser
Strategie in mehrere Schritte unterteilt. Zunächst werden aus der Elternpopulation
Gruppen zur Erzeugung der Nachkommen herangezogen. Diese bestehen jeweils aus
ρ Individuen2 . Dies bedeutet, dass jeweils λ Gruppen (aus ρ Individuen) gebildet
2
Im Standardfall ist ρ=2
17
2 Evolutionsstrategien
werden. Die Wahl der Eltern erfolgt zufällig mit gleicher Wahrscheinlichkeit für jedes
Elter.
Im nächsten Schritt werden die Gruppen durch die modellhafte Simulation der Erzeugung der haploiden Zellen der Keimbahn auf einzelne Duplikate reduziert. Dies
kann nach zwei unterschiedlichen Rekombinationsstrategien geschehen:
1. Das neue Individuum entsteht durch den Mittelwert der Zahlen die bei den
Duplikaten an der entsprechenden Stelle stehen.
2. Das neue Individuum entsteht durch eine diskrete Vertauschung der reellen
Zahlen auf den Vektoren3 .
Die bisher eingeführten Evolutionsstrategien ermöglichen eine Anzahl unterschiedlicher Varianten. Durch die Wahl der ganzzahligen Parameter µ, ρ und λ können bereits Evolutionsstrategien mit beliebig großen Populationen, frei wählbaren
Selektionsdruck und zyklischen Wachstum simuliert werden. Durch den zusätzlichen Einsatz der ”+” und ”,” Varianten lassen sich zudem noch eine Fülle von
Rekombinations- und Selektionsstrategien realisieren.
2.3. Mutation
Die Evolutionsstrategien basieren auf dem Grundgedanken der Nachkommenerzeugung durch die DNS-Selbstverdopplung. Bei der Erzeugung von Nachkommen werden aus dem Ausgangsindividuum jeweils ein oder mehrere Duplikate erzeugt, welche
anschließend mutiert werden, indem auf das Duplikat ein Zufallsvektor addiert wird,
dessen Werte um Null schwanken. Dabei wird darauf geachtet, dass kleine Änderungen des Erbgutes (Vektorkomponenten) mit größerer Wahrscheinlichkeit auftreten
als große. Bei dieser Mutationsvariante kann man noch nicht von einer adaptiven
Schrittweitenregelung sprechen, da die Varianz der Zufallsänderungen über alle Generationen konstant ist. Es fehlt ein Mechanismus, der in Abhängigkeit von dem
jeweiligen Erfolg oder Misserfolg der Suche die Varianz der Zufallsänderungen verändert, um möglichst schnell zum Optimum zu gelangen.
Satz 2.1 (1/5 Erfolgsregel) Der Quotient aus den erfolgreichen Mutationen zu
allen Mutationen sollte mindestens 1/5 betragen. Ist der Quotient größer als 1/5,
3
Die Vektoren tauschen untereinander per Zufall ihre Parameterwerte auf den sich entsprechenden
Positionen der Vektoren aus.
18
2.3 Mutation
so sollte die Streuung der Mutationen erhöht werden; ist der Quotient geringer so
sollte die Streuung verringert werden.
Die Idee hinter dieser Heuristik ist die Veränderung der Schrittweite im Suchraum:
wenn der Quotient größer als 1/5 ist, werden größere Schritte im Raum vollzogen, da
man sich in einem Gebiet des Hyperraums befindet, in dem Fortschritte wahrscheinlicher sind als zu erwarten wäre; wenn der Quotient kleiner 1/5 ist, werden Kleinere
vollzogen, da im Mittel mehr als 5 Mutationen durchgeführt werden müssen, um
eine Verbesserung der Bewertungsfunktion zu erzielen.
Die 1/5-Erfolgsregel ist lediglich eine grobe Faustregel für die Adaption der Schrittweite. Nachteilig ist jedoch, dass sie nicht problemabhängig automatisch angepasst
wird und zu einer frühzeitigen Konvergenz des Verfahrens und damit zu einem lokalen Optimum führt.
19
3. Genetische Algorithmen
Als Ingo Rechenberg die Evolutionsstrategien an der TU Berlin entwickelte, beschäftigte sich auch John Holland mit der computergestützten Simulation der biologischen Evolution und begründete sein Modell der genetischen Algorithmen. Beide
Verfahren wurden dabei unter verschiedenen Gesichtspunkten und vollkommen unabhängig voneinander entwickelt. Dabei unterscheiden sich genetische Algorithmen
und Evolutionsstrategien nur in wenigen Einzelheiten. Während Rechenberg primär
die Lösung von Problemen mit realzahl-codierten Parametersätzen verfolgte, interessierte sich Holland für die grundsätzliche Struktur, mit der in der natürlichen Evolution Informationen gespeichert und verarbeitet werden. Genetische Algorithmen
gehen folglich genauer auf die natürlichen Gegebenheiten der natürlichen Evolution
ein.
Die Frage, auf welche Art und Weise die Natur genetische Informationen speichert
und wie die jeweiligen Prozesse auf diesen genetischen Daten operieren, faszinierte
J. Holland ebenso wie die Tatsache, dass sich das Leben in derart vielfältiger Form
allein auf Basis des genetischen Codes und den damit verbundenen evolutionären
Prozessen entwickeln konnte. Diese Form der Selbstorganisation und Adaption wollte er nachvollziehen und auf technischem Weg mit Hilfe von Computersimulationen
nutzbar machen. Dabei widmete er sich nicht nur der Theorie, sondern stellte auch in
seinem Hauptwerk Adaptation in Natural and Artifical Systems verschiedene praktische Anwendungsmöglichkeiten seiner Theorien vor: in Bereichen wie der Ökonomie,
der Spieltheorie, der Muster- und Gestalterkennung, des maschinellen Lernens und
der künstlichen neuronalen Netzwerke. Zudem hat er erkannt, dass sich genetische
Algorithmen insbesondere zur Lösung komplexer Optimierungsprobleme eignen.
3.1. Beschreibung eines genetischen Algorithmus
Da es für genetische Algorithmen keine formale Notation gibt, soll das Grundgerüst
eines genetischen Algorithmus in Form eines Pseudocodes beschrieben werden (vgl.
21
3 Genetische Algorithmen
Abbildung 3.1). Auch bei den genetischen Algorithmen wurden im Laufe der Zeit
eine große Zahl von Varianten entwickelt, die sich primär in der Codierung und den
verwendeten Verfahren (Heiratsschema, Rekombination, Mutation und Ersetzungsschema) unterscheiden. Der nachfolgend dargestellte Programmabschnitt beschreibt
den üblichen Ablauf. Problemspezifische Codierung bedeutet hier, dass der zu opti-
Wähle problemspezifische Individuencodierung
Initialisiere Individuen der Startgeneration zufällig
do {
x
Bewerte Individuen mit Bewertungs-/Fitnessfunktion
x
Selektiere Elternpaare nach Heiratsschema
x
Erzeuge Nachkommen durch Rekombination
x
Mutiere die erzeugten Nachkommen
x
Ersetze Individuen der aktuellen Generation nach
x
Ersetzungsschema
} while Abbruchbedingung trifft nicht zu
Abbildung 3.1.: Pseudocode eines genetischen Algorithmus
mierende Parametersatz der Problemstellung in Form eines binären Parametervektors codiert wird. Die im Pseudocode angedeutete Initialisierung der Startgeneration
erzeugt Individuen mit zufällig konfigurierten Chromosomen. Eine so generierte Generation 0 enthält eine zufällige Menge an Punkten im Suchraum.
Nach der Initialisierung der Generation beginnt der Optimierungsprozess. Zunächst
werden die Individuen bewertet und Eltern ausgewählt. Durch Rekombination dieser werden systematisch neue Lösungen erzeugt, die gegebenenfalls mutiert werden.
Zum Schluss werden Individuen ausgewählt, die in die nächste Generation übernommen werden sollen.
Eine Abbruchbedingung kann auf verschiedene Arten und Weisen formuliert werden. Entweder wäre eine Endbedingung durch die Angabe eines mindestens zu erreichenden Qualitätswertes denkbar, oder aber auch beispielsweise eine maximale
Rechenzeit für die Simulation oder eine maximale Anzahl an Generationsschritten.
Die letztere Variante kann dazu führen, dass das Finden einer optimalen Lösung
durch einen frühzeitigen Abbruch verhindert wird. Vorstellbar wäre auch den evo-
22
3.2 Codierung
lutionären Lauf nach einer gewissen Anzahl von Generationsschritten zu beenden,
wenn keine weitere Verbesserung eingetreten ist.
3.2. Codierung
Der auffälligste Unterschied der genetischen Algorithmen zu den Evolutionsstrategien besteht darin, dass die Chromosomen einer Generation in der Regel als binäre
Vektoren 1 codiert sind. Wie in Kapitel 2 besprochen wurde basieren Evolutionsstrategien auf der kompaktesten Form einer Codierung: reelle Zahlen. Genetische Algorithmen codieren dagegen standardmäßig die Information nicht so kompakt wie
möglich, sondern so breit wie möglich (binär).
Für das bessere Verständnis der nachfolgenden Kapitel soll auf die binäre Codierungsform näher eingegangen werden.
3.2.1. Binärcode
Es werden ausschließlich Vektoren auf der Grundmenge M:={0,1} betrachtet. Ein
solcher binärer Vektor x aus M heißt Chromosom 2 . Mn und jede Teilmenge N von Mn
wird als Generation bezeichnet. Die i-te Position eines Chromosoms x = <...,xi ,...>
∈ Mn heißt das i-te Gen des Chromosoms. Der jeweilige Wert eines Gens heißt
Allel. Die Gene entsprechen damit, wie bei den Evolutionsstrategien Variablen, die
als Platzhalter dienen. Die Allele sind die jeweiligen Werte der Variablen.
In der praktischen Anwendungen bedeutet dies, dass die Information zunächst in
x = < 1, 0, 1, 1, 0, 1, 0, 0 >
x ist ein Chromosom mit 8 Genen
x = < < 1, 0, 0, 1 >, < 0, 0, 1 >, 1 >
x ist ein Chromosom mit 3 Genen
Abbildung 3.2.: Beispiele der GA Codierung
geeigneter Form binär codiert werden muss. Die Codierung der Individuen muss
1
2
Die Form der Codierung ist aber immer abhängig von der Problemstellung.
(n≥1); Schreibweise: x=<x1 ,x2 ,...,xn >
23
3 Genetische Algorithmen
mit den genetischen Operationen, die auf diesen Individuen durchgeführt werden,
optimal abgestimmt sein, anderenfalls kann der Erfolg des genetischen Algorithmus
nicht sichergestellt werden.
Eine binäre Codierung birgt den Vorteil, dass ihre Informationen schnell verarbeitet
werden können. Abhängig von den zu speichernden Variablen ist die binäre Speicherung wesentlich effizienter als eine Speicherung in Form von reellen oder natürlichen
Zahlen. Große Populationen würden somit relativ wenig Speicher benötigen. Dies
resultiert ebenfalls in einer beschleunigten Verarbeitung.
Nachteil einer binären Codierung ist die Tatsache, dass eine reelle Zahl, die Werte
aus einem vorgegebenen reellen Intervall annehmen kann, durch eine einzige Variable und damit durch ein einziges Gen repräsentiert werden kann, währenddessen bei
binären Codierungen dies nicht möglich ist, da eine binäre Variable nur 2 Werte
annehmen kann und somit mehrere Bitpositionen zur Darstellung benötigt werden.
Dadurch wird der potentielle Speichervorteil einer binären Codierung wieder kompensiert.
Ein weiteres Problem stellt die Positionsabhängigkeit der Codierung dar. Das folgende Beispiel erläutert die Problematik: zur Darstellung von 8 natürlichen Zahlen
werden minimal 4 Bit benötigt. Die natürliche Zahl 7 ist binär durch 0111 codiert.
Die nächste Zahl (8) hat im Dualsystem die Gestalt 1000. Im direkten Vergleich
der aufeinander folgenden Zahlen 7 und 8 (0111 und 1000) sind alle 4 Binärstellen
verschieden. Beim Übergang von 7 auf 8 müssen demnach sämtliche Bitpositionen
invertiert werden. Dieser Effekt tritt bei jeder Zweierpotenz 2n auf und wird mit der
Größe von n weiter verstärkt (z.B. 1023 → 01111111111 und 1024 → 10000000000).
Dieses Beispiel verdeutlicht, dass nicht zwingend kleine Änderungen an einer Codierung entsprechend zu kleinen Änderungen an einer anderen Codierung führen.
Dieses triviale Faktum kann für die Konvergenz eines genetischen Algorithmus erhebliche Folgen haben. Beispielsweise soll ein Optimierungsproblem zu lösen sein.
Das Optimum liegt genau bei 1024. Bekannt sei lediglich, dass das Optimum in einem Bereich zwischen 500 und 2000 liegt. Bei einer reellen Codierung ähneln sich
zwei Zahlen, die nahe bei 1024 liegen (1022,887 und 1024,088). In diesem Fall ist
zu erwarten, dass durch eine Rekombination der beiden Näherungswerte und durch
die Mutationen das Optimum 1024 schnell und beliebig genau approximiert wird.
Die vergleichbare Situation mit einer Binärcodierung verdeutlicht, dass zwei Binärzahlen die nahe 1024 sind (01111111110 und 10000000101) sich nicht mehr ähneln
und jede Rekombination dieser beiden Binärwerte zu einem wesentlich schlechteren
24
3.2 Codierung
Wert führen. Auch durch Mutation ist keine Verbesserung zu erwarten, da die Wahrscheinlichkeit sehr gering ist, nur die letzte und drittletzte Stelle der zweiten Approximationszahl 10000000101 auf Null zu mutieren, aber andererseits keine weitere
Position auf 1. Bei der ersten Approximationszahl 01111111110 ist die Wahrscheinlichkeit einer sich positiv auswirkenden Mutation noch geringer.
Zur Vermeidung der Sprünge bei der binären Codierung natürlicher Zahlen sind
spezielle Codes entwickelt worden, bei denen beim Übergang von n auf n+1 im Dezimalcode jeweils nur ein Bit verändert wird. Der bekannteste Binärcode mit dieser
Eigenschaft ist der so genannte Gray-Code.
Aufgrund der angesprochenen Probleme mit dem
n binär Gray-Code
Standardbinärcode ist der Gray-Code bei vielen
0 0000
0000
praktischen und theoretischen Problemen dem
1 0001
0001
gewöhnlichen Binärcode vorzuziehen. Der gewöhn2 0010
0011
liche Binärcode hat noch einen weiteren Nach3 0011
0010
teil: die Positionen innerhalb des Codes sind nicht
4 0100
0110
gleichwertig. Die führenden Stellen codieren grö5 0101
0111
ßere Zweierpotenzen als die hinteren Bitpositio6 0110
0101
nen. So ist der Code für die Dezimalzahl 10 im
7 0111
0100
Binärcode wie folgt aufgebaut:
8 1000
1100
1010 = 10102 = 1 ∗ 23 + 0 ∗ 21 + 1 ∗ 21 + 0 ∗ 20
Abbildung 3.3.: Graycode
Diese Eigenschaft des Binärcodes führt teilweise zu erheblichen Problemen bei der
Rekombination und Mutation. Wird beispielsweise bei der Binärzahl 10000000001
die erste Stelle mutiert und auf Null gesetzt, so ergibt sich 00000000001, also die
Zahl 1. Wird hingegen die letzte Stelle der Binärzahl von 1 auf 0 mutiert, so ist
das Ergebnis 1024. Im ersten Fall verändert eine einzige binäre Mutation demnach
den Wert der Zahl um einen Betrag von 1024, im zweiten hingegen gerade um 1.
Um diesen Effekt zu kompensieren, muss innerhalb von genetischen Algorithmen oft
mit Mutationen gearbeitet werden, bei denen die Mutationswahrscheinlichkeit eine
Funktion der Position der einzelnen Gene ist.
3.2.2. Länge
Genetische Algorithmen mit einer Codierungsform fester Länge können viele Probleme lösen. Der größte Nachteil dieser Repräsentationsklasse ist aber ihr Mangel
25
3 Genetische Algorithmen
an Variabilität. Die ursprüngliche Wahl der Codierungslänge zu Beginn des Evolutionslaufs limitiert die Anzahl der internen Zustände und als Konsequenz die Lernfähigkeit des System. Um dieser Einschränkung entgegenzuwirken können Repräsentationen variabler Länge eingeführt werden.
3.2.3. Junk DNS
Molekularbiologen haben in der DNS lange Ketten von nicht funktionalen Nukleotiden entdeckt, welche keine Proteine codieren (vgl. Kapitel 1: Exons und Introns).
Weshalb Introns in der natürlichen Evolution nicht gelöscht wurden, obwohl sie nicht
zur Proteinproduktion beitragen, ist bislang noch ungeklärt.
Untersuchungen haben ergeben, dass Introns das Crossing-over bei genetischen Algorithmen effektiver gestalten. Sie erhöhen die Anzahl an Kreuzungspunkten. Die
exakte Quantifizierung des Intron-Effekts bzgl. genetischer Algorithmen ist aber
dennoch noch offen und bedarf weiterer Forschung.
3.3. Bewertung und Fitness
Ebenso wie die Codierung selbst ist auch die Bewertung der Individuen einer Generation problemabhängig. Die Bewertungsfunktion legt das Optimierungskriterium und -ziel fest. Ein genetischer Algorithmus versucht stets für die Bewertungsfunktion einer Problemstellung einen optimalen Parametersatz zu erzeugen. Ob die
Bewertungsfunktion dazu minimiert oder maximiert werden muss, hängt von der
Problemstellung ab. Die Bewertungsfunktion misst damit die Qualität einer möglichen Lösung - eines Individuums - bzw. wie weit ein Individuum von dem gesuchten Optimum entfernt ist. Diese Bewertung eines Individuums wird zunächst
in einem Fitnesswert umgerechnet (Skalierung). Auf der Basis dieses Wertes wird
dann entschieden, mit welcher Wahrscheinlichkeit ein Individuum an dem Prozess
der Erzeugung von Nachkommen teilhaben darf. Die Gleichsetzung von Fitness und
Bewertung eines Chromosoms ist streng genommen falsch, da die Bewertungsfunktion misst, wie gut ein Chromosom das Optimum approximiert, die Fitness hingegen
gibt an, wie sich aus dieser Güte die Chance für das Chromosom errechnet, sich
in der nächsten Generation zu reproduzieren. Bewertung und Fitness sind daher
voneinander unabhängige Begriffe. Häufig wird aber dennoch nicht zwischen den
Begriffen unterschieden. Grund hierfür ist, dass die Bewertung und Fitness durch
26
3.3 Bewertung und Fitness
die gleiche Funktion errechnet werden kann, oder die Fitnessfunktion oft lediglich
eine Transformation der Bewertung darstellt.
Im Folgenden sei n die Anzahl der Individuen der aktuellen Generation, bi die BeP
wertung von Individuum xi und B := ni=0 bi die Summe der Bewertungen aller
Individuen.
Identifiziert man die Fitness eines Individuums mit seiner Bewertung, so lässt sich
dies wie folgt ausdrücken: f (bi ) = bi . In diesem Fall entspricht die Fitness direkt der
Bewertung.
Existieren in einem Generationenlauf jedoch ein paar außergewöhnliche Individuen,
würden diese die restlichen mittelmäßigen Individuen verdrängen. Dies resultiert
in einer frühzeitigen Konvergenz. Eine Skalierung hilft diese frühe Dominanz von
außergewöhnlichen Individuen zu vermeiden.
Am gebräuchlichsten sind die folgenden Funktionen.
3.3.1. Proportionale Skalierung
Bei der proportionalen Fitness wird die Fitness eines Individuums proportional zum
Verhältnis der Bewertung des Individuums zur Summe der Bewertungen aller Chromosomen einer Generation errechnet:
f (bi ) := bi /B
(3.1)
3.3.2. Lineare Skalierung
Bei der linearen Skalierung wird die Fitness eines Individuums aus der Menge der
Bewertungen der aktuellen Generation entsprechend folgender linearer Funktionsgleichung errechnet:
f (bi ) := x ∗ bi + y
(3.2)
Ziel dieser Skalierung ist es, die durchschnittliche Bewertung der durchschnittlichen
Fitness anzugleichen (bavg =f
ˆ avg ). Hieraus folgt, das fmax = cmult ∗ bavg ist, wobei
cmult eine Konstante beschreibt, welche die erwarteten Kopien für das beste Individuum repräsentiert. Für kleine Populationen (n = 50 - 100) ist cmult mit den Werten
1,2 bis 2,0 zu definieren. In einem fortgeschrittenen Lauf kann jedoch der Fall eintreten, dass einige Individuen unter dem Populationsdurchschnitt und -maximum
liegen (Durchschnitt und Maximum liegen dicht bei einander). Nach einer linearen
27
3 Genetische Algorithmen
Abbildung 3.4.: Lineare Skalierung
Skalierung würde die Fitness solcher Individuen negativ und die erforderliche NichtNegativität wäre verletzt. In solchen Fällen muss die Fitness auf ihren minimalen
annehmbaren Wert 0 gesetzt werden.
bi bavg ⇒ fb(i) = fmin = 0
(3.3)
Das Berechnungsschema zur Bestimmung von x und y sei folgendermaßen:
Gegeben seien die Werte von cmult , fmax , favg , fmin . Zunächst wird die minimale
Fitness auf Nicht-Negativität getestet:
fmin > (cmult ∗ favg − fmax )/(cmult − 1, 0)
(3.4)
Im hieraus resultierenden Fall 1 ergeben sich x und y wie folgt:
x = (cmult − 1, 0) ∗ favg /(fmax − favg )
(3.5)
y = favg ∗ (fmax − cmult ∗ favg )/(fmax − favg )
(3.6)
Fall 2 errechnet die Wert von x und y noch dem Schema:
x = favg /(favg − fmin )
(3.7)
y = fmin ∗ favg /(favg − f min)
(3.8)
3.3.3. Dynamic Power Law Skalierung
Für die Konstruktion eines Skalierungsmechanismus, der auf die Beziehung zwischen
var (t)
Varianz und Mittelwert einer Population spt = ffavg
und dem Populationsalter3 t
(t)
aufbaut, konstruierte Michalewicz k, welches sich von kleinen zu großen Werten
3
Anzahl der Generationen
28
3.4 Genetische Operatoren
im Verlauf des Populationsalters entwickelt, so dass k größer ist für Probleme mit
kleinen spt . Um den Aufwand an Berechungen zu reduzieren, soll spt lediglich für
die Startgeneration berechnet werden (sp0 ).
k=(
sp∗ α
t
π
sp∗ p
)1 ∗ tanp2 ∗(
) ∗(
∗ )
s0
sp0
T +1 2
(3.9)
sp∗ = 0, 1 ist hierbei durch Michalewicz experimentell ermittelt worden. p1 = 0, 05
gibt die Influenz von sp0 auf k an, p2 = 0, 1 und α = 0, 1 bestimmen die Veränderungsgeschwindigkeit von k und T ist die Anzahl der gesamten Generationen im
Evolutionslauf. Michalewicz berichtet durch dieses Skalierungsverfahren eine bessere
Effizienz des genetischen Algorithmus.
3.4. Genetische Operatoren
Die Reproduktionsphase eines genetischen Algorithmus kann in vier definierte Algorithmen untergliedert werden, den Selektions-, Heirats-, Rekombinations- und
Mutations-Algorithmus.
3.4.1. Selektions-Schema
Das Selektions-Schema legt fest welche Individuen einer Population zur Erzeugung
neuer Chromosomen (Crossing-over) herangezogen werden.
Das klassische Selektions-Schema wählt die Kandidaten für die Erzeugung von Nachkommen mit
einer Wahrscheinlichkeit aus, die proportional
zu ihrer Fitness ist. Dadurch wird erreicht, dass
Nachkommen mit hoher Fitness in der nächsten Generation mit größerer Wahrscheinlichkeit
vertreten sind als durchschnittliche Elemente.
Ziel dieses Prozesses ist es, über die Generationen hinweg ein kontinuierliches Ansteigen der
Qualität der Populationen zu erreichen. Dieses
Abbildung 3.5.: Roulette Wheel
Roulette-Wheel Verfahren ist der Standard Selektionsalgorithmus bei den genetischen Algorithmen. Es stellt sicher, dass die Individuen einer Population eine zu ihrer Fitness
proportionale Chance für die Fortpflanzung erhalten. Dies bedeutet jedoch nicht,
29
3 Genetische Algorithmen
dass nur überdurchschnittlich gute Individuen zur Nachkommenerzeugung herangezogen werden. Auch Individuen mit geringer Fitness erhalten prinzipiell die Chance
sich fortzupflanzen. Allerdings ist die Wahrscheinlichkeit hierfür wesentlich4 geringer
als bei Individuen mit hohen, überdurchschnittlichen Fitnesswerten. Dieser Zusammenhang wird in Abbildung 3.5 verdeutlicht. Das Individuum mit dem Fitnesswert
5 hat eine höhere Wahrscheinlichkeit selektiert zu werden als jenes mit Wert 1.
3.4.2. Heirats-Schema
Das Heirats-Schema bestimmt welche Individuen rekombiniert werden. In [Gol89]
werden mehrere verschiedene Heirats-Schemata definiert:
Random Mating Die Heiratspartner werden mit gleicher Wahrscheinlichkeit zufällig ausgewählt.
In-Breeding Die Verwandten werden verheiratet.
Line-Breeding Ein leistungsstarkes Individuum vermehrt sich mit einer Population
von Individuen; die Kinder werden als Eltern selektiert.
Out-Breeding Individuen mit unterschiedlichen Phänotypen werden verheiratet.
Self-Fertilization Ein Individuum wird mit sich selbst kombiniert.
Positive Assortive Mating Ähnliche Individuen werden verheiratet.
Negative Assortive Mating Unähnliche Individuen werden verheiratet.
In den meisten Implementierungen genetischer Algorithmen ist das Schema Random
Mating das Mittel der Wahl.
3.4.3. Rekombination der Chromosomen
Die genetischen Algorithmen legen Ihren Schwerpunkt auf die problemabhängigen
Rekombinationsschemata. Ziel von Crossing-over Verfahren ist es, den Suchraum
effizient zu durchlaufen. Wird ein geeignetes Schema eingesetzt, so ist zu erwarten,
4
im Laufe der Generationen exponentiell
30
3.4 Genetische Operatoren
dass Regionen des Suchraums mit höherer durchschnittlicher Güte wesentlich schneller erreicht und durchlaufen werden als durch rein zufälliges Suchen. Die einfachste
Form der Rekombination ist das One-Point-Crossover 5 :
Für jedes nach dem Heiratsschema selektierte Chromosomenpaar a1 und
a2 gilt:
1. Generiere eine gleichverteilte, natürliche Zufallszahl p ∈
[1,l(ai )[
2. Generiere ein neues Chromosomenpaar b1 und b2 :
Wenn i ≤ p dann
b1 (i) := a2 (i)
b2 (i) := a1 (i)
sonst
b1 (i) := a1 (i)
b2 (i) := a2 (i)
Abbildung 3.6.: One-Point-Crossover Schema
Eine etwas komplexere Variante des One-Point-Crossover stellt das Two-PointCrossover -Schema dar. Dieses wird in Suchräumen verwendet, bei denen die Suche
in zwei Hyperebenen durchgeführt werden muss. Die Einführung eines Two-PointCrossover (vgl. Abbildung 3.7) bringt im Allgemeinen eine schnellere Konvergenz
des Algorithmus mit sich.
Bei einen Two-Point-Crossover können ebenfalls Hyperebenen existieren, die auch
mit diesem erweiterten Crossover-Schema aus zwei Hyperebenen nicht erzeugt werden können. In solchen Fällen würde ein 3-Point-Crossover oder die verallgemeinerte
Form ein n-Point-Crossover die Lösung bringen.
Will jedoch sichergestellt werden, dass jeder Punkt des n-dimensionalen Raumes konstruierbar ist, so ist das Schema nach Abbildung 3.8 anzuwenden (ZufallsSchablonen Crossing-over ).
Weitere Formen von Rekombinationsstrategien sind in der Literatur zu finden.
5
Für die folgenden Schemata sei l(x) eine Funktion zur Berechnung der Länge eines Vektors x.
31
3 Genetische Algorithmen
Für jedes nach dem Heiratsschema selektierte Chromosomenpaar a1 und
a2 gilt:
1. Generiere zwei gleichverteilte, natürliche Zufallszahlen p1 , p2
∈ [1,l(ai )[
2. Generiere ein neues Chromosomenpaar b1 und b2 :
Wenn p1 ≤ i ≤ p2 dann
b1 (i) := a2 (i)
b2 (i) := a1 (i)
Wenn p2 < i oder i < p1 dann
b1 (i) := a1 (i)
b2 (i) := a2 (i)
Abbildung 3.7.: Two-Point-Crossover Schema
3.4.4. Mutationen
Im Vergleich zu den Evolutionsstrategien dienen die Mutationen bei den genetischen
Algorithmen nicht als zusätzliche Suchoperatoren. Die Mutationswahrscheinlichkeit
ist ein externer Parameter und in der Regel nicht Bestandteil des Codes. Nichtsdestoweniger sind Mutationen nicht unterzubewerten. Eine typische Mutation für ein
Chromosom x =< x1 , . . . , xn > verfährt nach dem in Abbildung 3.9 dargestellten
Schema (Gleichverteilte Mutation).
Eine Abart dieser Variante ist die so genannte Gleichverteilte Mutation/2. Bei dieser ist die Mutationswahrscheinlichkeit pro Gen, d.h. die Wahrscheinlichkeit, dass
der Wert des betreffenden Gens verändert wird, im Mittel nur halb so groß wie bei
der obigen Gleichverteilten Mutation.
In vielen praktischen Anwendungen ist es wichtig, die Genmutation pro Chromosom nicht mit gleicher Wahrscheinlichkeit für alle Gene auszuführen. Der Grund
liegt in der oben besprochenen positionsabhängigen Wertigkeit einzelner Gene bei
der Standard-Binärcodierung. Deshalb müssen bestimmte Positionen eines Chromosoms häufig mit größerer oder kleinerer Wahrscheinlichkeit mutiert werden. Z.B.
kann eine Normalverteilung der Mutationswahrscheinlichkeit über das Chromosom
32
3.4 Genetische Operatoren
Für jedes nach dem Heiratsschema selektierte Chromosomenpaar a1 und
a2 gilt:
1. Generiere einen binären Zufallsvektor z mit l(z) = l(ai ) (zi = 1
oder zi = 0)
2. Generiere ein neues Chromosomenpaar b1 und b2 :
Wenn zi = 1 dann
b1 (i) := a1 (i)
Wenn zi = 0 dann
b1 (i) := a2 (i)
Setze
b2 (i) := 1 − b1 (i)
Abbildung 3.8.: Zufalls-Schablonen Crossing-over
1. Wähle eine gleichverteilte Zufallszahl z mit 1 ≤ z ≤ n.
2. Betrachte das Gen xz
3. xz := 1 − xz
Abbildung 3.9.: Gleichverteilte Mutation
verwendet werden. Dies würde einen zur Abbildung 3.9 entsprechenden Algorithmus
ergeben6 .
Das allgemeinste Schema dieser Art entsteht, wenn pro Position eine Zufallsentscheidung über die Mutation getroffen wird. Auf diesem Schema beruht die PositionsMutation (vgl. Abbildung 3.10). In dieser kann für jede Genposition auf dem Chromosom eine individuelle Mutationswahrscheinlichkeit festgelegt werden.
Das zufällige Kippen von einzelnen Positionen eines Chromosoms wirkt sich bei einer geringen Mutationswahrscheinlichkeit und sehr großen Chromosomen oft nur
unmerklich auf die Fitness eines Chromosoms aus.
Bei den genetischen Algorithmen wirkt die Mutation als Hintergrund-Operator, der
6
Es lässt sich hier analog ein Schema Normalverteilte Mutation/2 definieren
33
3 Genetische Algorithmen
1. Wähle für jede Position (Gen) xi des Chromosoms eine Zahl ai mit
0 ≤ ai ≤ 1
2. Wähle für jede Position xi eine Zufallszahl bi mit 0 ≤ bi ≤ 1
3. Wenn ai ≤ bi dann xi := 1 − xi
Abbildung 3.10.: Positions-Mutation
ein gewisses Rauschen in den Suchprozess einführt, um eine zu frühzeitige Konvergenz zu vermeiden.
Ähnlich wie bei den Evolutionsstrategien lassen sich die Mutationen bei einer etwas
allgemeineren Definition der genetischen Algorithmen als aktive, zusätzliche Suchoperatoren nutzen.
3.4.5. Fortgeschrittene Operatoren
Inversion
Der unäre Inversions-Operator ersetzt einen zufällig gewählten Bereich eines Chromosoms durch dessen Umkehrung. Um wie erwartet arbeiten zu können, müssen
die Chromosome in einer positions-unabhängigen Weise codiert und das Crossingover angepasst werden, so dass nur Chromosome mit einer kompletten Anzahl von
Genen entstehen. Für den Fall einer positions-abhängigen Repräsentation kann ein
Operator entwickelt werden, welcher die Inversion und Kreuzung kombiniert.
Dominanz und Diploidie
Diploidie kann als Möglichkeit angesehen werden um ein Gedächtnis in die Struktur
eines Individuums einzubauen. Statt eines einzigen Chromosoms (haploide Struktur), das die Information über ein Individuum repräsentiert, kann eine Diploide
gebildet werden, welche aus einem Paar von Chromosomen besteht: die Auswahl
zwischen zwei Werten wird durch eine Dominanzfunktion vollzogen. Diploide Strukturen sind von besonderer Signifikanz in nicht stationären Umgebungen7 und für die
Modellierung komplexer Systeme.
7
z.B. zeit-abhängige Bewertungsfunktionen
34
3.5 Ersetzungsschema
Es existiert allerdings sowohl keine Theorie über den Einbau einer Dominanzfunktion in das System als auch keine experimentellen Daten in diesem Bereich.
3.5. Ersetzungsschema
Mit dem Heirats-Schema werden die Individuen für die Reproduktion ausgewählt.
Nach der Erzeugung der Nachkommen mittels Crossover und Mutation muss entschieden werden, was mit der bisherigen Generation geschehen soll. Diese Aufgabe
wird durch das Ersetzungsschema definiert. Die einfachste Form der Ersetzung ist
das so genannte Generational Replacement:
Ersetze die aktuelle Population vollständig durch ihre Nachkommen.
Abbildung 3.11.: Generational Replacement
Dieses Verfahren ist ungefähr vergleichbar mit der Komma-Variante der Evolutionsstrategien. Nachteil dieses Schemas ist, dass der Fall eintreten kann, dass sowohl
die Bewertung des besten Individuums der Nachfolgegeneration als auch die durchschnittliche Bewertung der neuen Generation schlechter ist als in der Elterngeneration. Die Bewertungsfunktion ist dann weder für das beste Individuum noch für
den Durchschnitt über die Generationen monoton steigend. Dieser Nachteil kann
durch den Vorteil kompensiert werden, dass durch den vollständigen Austausch der
Generationen die Dominanz einiger weniger guter Individuen der Ausgangspopulation durchbrochen wird. Das Risiko einer zu frühzeitigen Einschränkung der Suche
im Suchraum kann reduziert werden, jedoch nimmt gleichzeitig die Konvergenzgeschwindigkeit mit ab.
Um die Erhaltung der besten Individuen einer Population zu erreichen und damit
ein monotones Ansteigen der Bewertung über die Generationen zu gewährleisten
wurde das Prinzip der Eliten entwickelt:
Der Elitismus verhält sich reziprok zum Generational Replacement. Durch die Beibehaltung der n besten Chromosomen in der nächsten Generation kann es zu einem
Dominanzeffekt kommen, wenn der Unterschied der Güte zu den anderen Individuen
der neuen Generation sehr groß ist8 . Durch die proportional zur Fitness vorgenom8
Super-Individuum
35
3 Genetische Algorithmen
Übernehme die n besten Individuen (Elite) der aktuellen Generation
unverändert in die nächste Generation.
Abbildung 3.12.: Elitismus
mene Vermehrung dominieren die Nachkommen der Besten die nächste Generation.
Das Resultat kann eine suboptimale, zu homogene und damit zu frühzeitige Stagnation des Evolutionsprozesses sein. Um diesen Effekt zu verhindern oder abzuschwächen, kann mit einem schwachen Elitismus gearbeitet werden. Hierbei werden die n
Besten mutiert in die nächste Generation übernommen.
Übernehme die n besten Individuen (Elite) der aktuellen Generation in
mutierter Form in die nächste Generation.
Abbildung 3.13.: Schwacher Elitismus
Da üblicherweise die Populationengröße über die Generationen konstant gehalten
wird, muss in jeder Generation neu entschieden werden, welche Individuen aus der
aktuellen Generation zu entfernen sind. Die nächstliegende Lösung definiert das
Schema Delete-n-Last:
Ersetze die n schlechtesten Individuen der aktuellen Generation durch
n Nachkommen der Vorgängergeneration.
Abbildung 3.14.: Delete-n-Last
Ist der Wert von n in diesem Schema klein, d.h. n Populationsgröße, so spricht
man auch von einem Steady-State Ersetzungsschema. Für n = 1 erhält man eine
minimale Änderung pro Generation; für n = Populationsgröße das Generational
Replacement.
36
3.6 Kontrollgrößen
3.6. Kontrollgrößen
Genetische Algorithmen hängen von verschiedenen Parametern ab, welche in ihrer
Ausprägung entscheidenden Einfluss auf die Konvergenz und Effizienz des Evolutionslaufs haben können.
Populationsgröße und Generationenanzahl David Goldberg berichtet, dass die
erwartete Anzahl an Generationen bis zur Konvergenz eine logarithmische Funktion
der Populationengröße ist.
Konstante kontra variabler Populationengröße Der typische genetische Algorithmus verfährt mit einer konstanten Populationengröße. James E. Baker schlägt
einen genetischen Algorithmus mit einer dynamischen Populationsgröße vor, mit
dem Ziel vorzeitige Konvergenz zu vermeiden.
Terminierung Die natürliche Evolution ist ein Prozess mit offenem Ende. Für
genetische Algorithmen ist es unabdingbar ein Endekriterium zu formulieren. Die
häufigste Variante ist es, bis zu einer vorgegebenen Anzahl an Generationen zu laufen. Zusätzlich oder stattdessen kann ein Fitnesswert vorgegeben werden, bei dessen
Erreichen oder Überschreiten der Evolutionslauf beendet wird. Ebenfalls wäre eine
maximale Rechenzeit für die Simulation, wie auch die Beendigung des Laufs nach einer gewissen Anzahl von Generationsschritten, bei denen keine weitere Verbesserung
eingetreten ist, als Endekriterium vorstellbar.
Resultat Nach der Terminierung eines genetischen Algorithmus kann auf unterschiedliche Art und Weise das Ergebnis des Evolutionslaufs ermittelt werden. Entweder wird das Ergebnis durch:
• das beste Individuum der letzten Generation,
• eine Unterpopulation des besten Individuums der finalen Generation oder die
komplette finale Generation, oder
• das beste Individuum, das im Evolutionslauf gefunden wurde9 , definiert.
9
benötigt Elitismus
37
4. Evolutionsstrategien kontra
genetische Algorithmen
In den vorangegangenen Kapiteln wurden Evolutionsstrategien und genetischen Algorithmen beschrieben, welche nun im Folgenden verglichen werden (s. Tabelle 4.1).
Worin bestehen zunächst die Gemeinsamkeiten? Beide Verfahren arbeiten mit Populationen potentieller Lösungen und selektieren auf bestimmte Art und Weise entsprechend qualifizierte Individuen der Population nach ihrer Bewertung/Fitness. Dieses
Prinzip ist wie in Kapitel 1 auf Charles Darwin zurückzuführen und unter dem
Namen survival of the fitesst bekannt: auf der Basis selektierter Individuen neue,
bessere Populationen potentieller Lösungen erzeugen.
Worin bestehen aber die Unterschiede zwischen den beiden Ansätzen? Bei den Evolutionsstrategien stehen die Mutationsprozesse und die adaptive Schrittweitenregelung im Vordergrund; bei den genetischen Algorithmen hingegen die genetische
Reproduktion mit den verschiedenen Crossing-over Strategien.
Der wesentlichste Unterschied liegt jedoch in der Codierungsform. Evolutionsstrategen repräsentieren die Individuen einer Population durch reelwertige Vektoren,
wo hingegen die Anhänger um J. Holland ein Chromosom durch binäre Vektoren
darstellen. Für die Optimierung eines konkreten Problems ist zunächst die Wahl
der Codierung entscheidend. Jedoch kann das zu strenge Festhalten an der binären
Codierungsform der genetischen Algorithmen bei manchen Problemen dem Finden
einer Lösung entgegenwirken. Besteht zum Beispiel das zu lösende Problem darin
reelle Zahlenwerte zu approximieren, so ist die reelle Codierung der Binärcodierung
vorzuziehen, da sie für solche Probleme die kompakteste Form der Repräsentation
des zu lösenden Problems darstellt (s. Kapitel 3.2). Der Weggang vom genotypischen
Ansatz und die Annäherung des Phänotypischen zieht auch eine Anpassung mancher
problemabhängiger genetischer Mechanismen mit sich, wie die Mutationsschemata.
Das Invertieren eines einzelnen Bits muss z.B. zur Addition bzw. Subtraktion eines
zufälligen Wertes im Intervall [0; 1] abgeändert werden.
39
4 Evolutionsstrategien kontra genetische Algorithmen
Ein weiterer wesentlicher Unterschied besteht bei den Selektionsprozessen. Bei einer
(µ+λ)-Evolutionsstrategie werden zunächst aus µ Eltern λ Nachfolgern erzeugt, indem aus einer Urne die µ Besten, die Eltern der Nachfolgegeneration werden. Die
Auswahl der Eltern folgt nach einem deterministischen Schema: jeweils die µ besten
Individuen werden die neuen Eltern. Dies entspricht einem survival of the fittest im
wahrsten Sinne des Wortes.
Bei einem genetischen Algorithmus läuft dieser Selektionsprozess, insbesondere unter Verwendung des Roulette-Wheel-Verfahrens, anders ab: aus einer Ausgangspopulation werden n/2 Paare ausgewählt, die dann je zwei Nachkommen und damit
erneut eine Population mit n Individuen erzeugen. Dem Überleben des Stärkeren
entspricht hier die Auswahl der Paare. Die Eltern werden mit einer zur ihrer Fitness
proportionalen Wahrscheinlichkeit ausgewählt. Bei den Evolutionsstrategien werden
die Eltern hingegen mit der gleichen, von der Fitness unabhängigen Wahrscheinlichkeit für die Reproduktion selektiert.
Der letzte Unterschied zwischen beiden Verfahren ist die Selbstadaption gewisser
Steuerungsparameter (Mutationsschrittweite und korrelierte Mutationen), welche
bei den Evolutionsstrategien fest in das Verfahren integriert sind. Bei den genetischen Algorithmen wäre ein solcher Mechanismus denkbar, jedoch schwer zu realisieren: diese Parameter müssten in den Chromsomen codiert werden.
Ein direkter methodisch-einwandfreier Performance-Vergleich zwischen Evolutionsstrategien und genetischen Algorithmen ist auf Grund der oben genannten Unterschiede kaum möglich. Hinzu kommt, dass beide Verfahren stark von bestimmten
Parametereinstellungen (Codierung, Populationsgröße, usw.) abhängig sind. Wären
diese schlecht gewählt, so kann ein Verfahren nicht oder nur ungenügend konvergieren. Folglich müsste ein Vergleich die Parametereinstellungen mit berücksichtigen.
Evolutionsstrategien
Gewichtung
Codierung
Selektion
Parameter
Genetische Algorithmen
Survival of the Fittest
Mutationsprozesse
genetische Reproduktion
reelle Vektoren
binäre Vektoren
von Fitness unabhängig
proportional zur Fitness
Selbstadaption fest integriert Selbstadaption denkbar
Tabelle 4.1.: Evolutionsstrategien kontra genetische Algorithmen
40
5. Evolution von Populationen
Betrachtet man die Evolution aus einer makroskopischen Sicht, so ergeben sich weitere Möglichkeiten für die evolutionären Algorithmen: miteinander kommunizierende
und wettstreitende Populationen. Aus diesem Grund sollen hier drei unterschiedliche
Modelle vorgestellt werden.
5.1. Insel-Modell
In diesem Modell kann eine beliebige Anzahl von Populationen betrachtet werden.
Die Populationen sind kommunikativ voneinander getrennt (isoliert) und entwickeln
sich aus diesem Grund völlig unabhängig von einander. Jede Population führt in
sich einen Evolutionsprozess durch.
Dieses Modell besitzt trotz seiner Einfachheit eine gewissen Plausibilität. Es gibt
viele Bespiele für isolierte Insel-Populationen. Der wesentlichste Vorteil dieses Modells liegt darin mehrere Evolutionsläufe gleichzeitig durchzuführen und am Ende
das beste Individuum aus allen Insel-Populationen als Lösung zu verwenden.
5.2. Netzwerk-Modell
Ein Nachteil des Insel-Modells ist jedoch, dass sich die einzelnen Populationen nur
auf der Basis des genetischen Erbgutes entwickeln, das auf der Insel in der Anfangspopulation verfügbar ist. Sind die Populationen auf der Insel klein und die
Mutationsrate niedrig, so kann dies sehr schnell zu einer homogenen Population
führen.
Um diesen Nachteil entgegenzuwirken kann das Insel-Modell zu einem NetzwerkModell erweitert werden. Das Netzwerk-Modell besteht ebenfalls aus einer Menge
voneinander abgegrenzter Populationen, jedoch tauschen diese unter einander Individuen über feststehende Informationskanäle (Wanderungswege) aus. Das Netzwerk
41
5 Evolution von Populationen
ist starr und verändert sich nicht. Meist ist jede Population mit jeder anderen über
einen bidirektionalen Kommunikationskanal verbunden.
Durch den Austausch von Individuen unter den Populationen wird dieses Modell
langsamer als das Insel-Modell. Dieser Zeitverlust wird jedoch durch die Tatsache kompensiert, dass die Populationen durch die ständige Ein- und Auswanderung
von Individuen wesentlich langsamer stagnieren. Das global beste Individuum eines
Netzwerk-Modells wird daher in der Regel einen höheren Fitnesswert besitzen als
das beste Individuum aller Insel-Populationen.
Für den Austausch von Individuen zwischen den Populationen gibt es zwei wesentliche Ansätze: synchron oder asynchron. Beim synchronen Austausch werden die
Individuen immer gleichzeitig zu einem bestimmter Zeitpunkt ausgetauscht. Bei der
asynchronen Kommunikation hingegen tauschen die Populationen unabhängig voneinander zu verschiedenen Zeitpunkten Individuen aus.
Bei der Verwendung des Netzwerk-Modells muss berücksichtigt werden, dass noch
zusätzlich Parameter benötigt werden, welche beschreiben:
• wann Individuen zu den anderen Populationen verschickt werden sollen,
• wie viele Individuen verschickt werden sollen,
• welche Individuen verschickt werden sollen und
• wie die ankommenden Individuen in die neue Population aufgenommen werden
sollen
Da diese Parameter je nach Ausprägung zu unterschiedlichen Verhalten des Netzwerkes führen können, beschreibt das Netzwerk-Modell eigentlich nicht nur ein Modell,
sondern eine Familie von Modelle.
5.3. Kommunen-Modell
David Goldberg hat ein weiteres Modell vorgestellt, welches Populationen als eine
Kommune betrachtet. Als Vorbild für dieses Modell haben ihm menschliche Kommunen gedient. Jede Kommune besteht aus einer Menge von Häusern, in denen die
Individuen leben, und einem Stadtkern mit einigen sozialen, allen Individuen zugänglichen Einrichtungen. In den Häusern der Kommune findet die Erzeugung der
42
5.3 Kommunen-Modell
Nachkommen statt. Die Nachkommen treffen sich ab einem bestimmten Alter1 in
einer Single-Bar oder einem Heiratsinstitut im Stadtkern. Dort suchen sie sich einen
Heiratspartner2 . Wenn sie einen Partner gefunden haben, benötigen sie im nächsten
Schritt zur Erzeugung von Nachkommen eine Wohnung (Haus). Die Häuser sind
jedoch pro Gemeinde limitiert. Deshalb müssen sich die Paare über einen Makler
im Stadtkern mit den anderen Paaren um ein Haus streiten. Die Paare die in einer
Kommune keine Häuser erhalten, begeben sich zum Busbahnhof im Stadtkern und
fahren zu einer anderen Gemeinde.
Dieses Modell berücksichtigt durch seine realistische Gegebenheit soziale Strukturen und einen erweiterten Kampf ums Überleben, der durch zwei Ebenen bestimmt
wird: zum einen durch den Erfolg des Individuums in der Single-Bar bei der Suche
eines Partners und zum anderen durch den Wettbewerb um ein Haus.
Das Kommunen-Modell benötigt einen relativ hohen Kommunikationsaufwand innerhalb einer Population und viel zentrale Steuerungsfunktionen3 . Dieses Modell soll
Abbildung 5.1.: Kommunen-Modell
veranschaulichen, dass viele Möglichkeiten vorhanden sind um evolutionäre Algorithmen um Mechanismen zu erweitern. Jedoch muss dabei darauf geachtet werden, dass
diese Erweiterung nur dann sinnvoll ist, wenn durch sie effizientere Optimierungen
möglich sind, oder komplexere Probleme gelöst werden können.
1
abhängig von der Fitness oder der Generation
dies kann nach dem weiter oben beschriebenen Roulette-Wheel Verfahren geschehen
3
Stadtkern mit Makler und Bar, Verwaltung der Häuser etc.
2
43
Teil II.
Software-Entwicklung
45
6. Server für evolutionäre
Verfahren
In den Kapiteln 2 und 3 wurden zwei Ansätze evolutionärer Algorithmen – Evolutionsstrategien und genetische Algorithmen – erläutert. Aufgrund des an diese Diplomarbeit gestellten Umfangs erfuhren nicht beide Varianten eine softwaretechnische Realisierung. Die Entscheidung für genetische Algorithmen gründet in
der Tatsache, dass die amerikanische Schule um J. Holland und D. Goldberg nachvollziehbarer erschien bzgl. einer computer-gestützten Umsetzung der biologischen
Evolution.
Es ist im Hinblick auf die Bezeichnung des Projekts bzw. der Algorithmenbibliotheken vom Begriff genetisch abgewichen worden, da definitionsgemäß binäre Vektoren
als Codierungsform verwendet werden, jedoch in dieser Diplomarbeit ein Weggang
vom genotypischen und eine Annäherung an den phänotypischen1 Ansatz vollzogen worden ist. Aus diesem Grund wurde die allgemeinere Bezeichnung evolutionär
gewählt. In den nachfolgenden Kapiteln wird die Benennung der Algorithmen als
evolutionär bzw. genetisch im eigentlichen Sinn von genetisch unter der Prämisse
der abgeänderten Codierungsform verwendet.
Im Folgenden werden Konzepte und Funktionsweisen wichtiger Komponenten der
im Rahmen dieser Diplomarbeit zu erstellenden Pakete erläutert. Es wird jedoch
davon abgesehen, eine detaillierte Beschreibung der Programmquelltexte zu geben.
6.1. Pakete
Eine Kernaufgabe der Diplomarbeit war die Implementierung genetischer bzw. evolutionärer Verfahren für die Optimierung/Lösung diverser Probleme2 . Hierfür wurde zum einen eine Bibliothek zur Kapselung der problemunabhängigen Teile des
1
2
Chromosom als Vektor reeller Zahlen, als binärer/unärer Baum
Approximation einer natürlichen Zahl, Genetische Prognose, Steuerungsaufgaben eines Kfzs
47
6 Server für evolutionäre Verfahren
Algorithmus (EALib) und zum anderen eine zweite zur Kapselung der problemabhängigen Teile des evolutionären Algorithmus (EAServer ) geschrieben. Der Ansatz
beide Komponenten des Algorithmus durch eine einzige Bibliothek zu kapseln, wurde nach sorgfältiger Prüfung verworfen. Er hätte bedingt, dass für jede Änderung
bzgl. eines Problemfeldes3 der gesamte Algorithmus neu kompiliert werden muss.
Durch die software-technische Umsetzung dieser Trennung beider Teile wurde somit
eine bessere Wartbarkeit des Systems erreicht. Darüber hinaus beinhaltet die EAServer -Bibliothek eine Komponente zur Codierung der Serverfunktionalität, sowie
ein Wrappermodul, welches Daten aus den Bibliotheken für eine Benutzerschnittstelle bereitstellt. Dieser Wrapper wurde unter zur Hilfenahme des Java Native
Interface (vgl. Kapitel 6.3.1) geschrieben. Das GUI-Projekt (EAServerUI ) wurde
augrund der Anforderung der Plattformunabhängigkeit in der Hochsprache Java
verfasst. Kernkomponente der Serverfunktionalität ist ein Kommunikationsmodul,
welches ermöglicht über diverse Kommunikationstechnologien verschiedene Klienten
anzubinden. Im Fall der Diplomarbeit wurde eine plattformunabhängige SocketBibliothek (SocketCPI ) geschrieben, welche für Unix- und Windows-Systeme Funktionen für eine TCP-Kommunikation bereitstellt. Sie ermöglicht die Anbindung von
Visualisierungs- oder Simulations-Clients für eine Optimierung/Lösung verschiedener Problemfelder.
Die Pakete - EALib, EAServer, EAServerUI - bilden den im Rahmen dieser Diplomarbeit entwickelten Server für evolutionäre (genetische) Algorithmen. Zusammen mit
den optionalen Clients bildet diese Software die Evolutionary Algorithm Applications.
Abbildung 6.1.: Pakete
3
Änderung des Chromosoms, Mutation und/oder Crossing-over
48
6.2 Bibliothek für evolutionäre Algorithmen
6.2. Bibliothek für evolutionäre Algorithmen
6.2.1. Komponenten
Die Bibliothek zur Kapselung evolutionärer Algorithmen (EALib) wurde in drei
Komponenten untergliedert: Kernel, Steuerungs- und Bewertungsmodul (vgl. Abbildung 6.2).
Der Kernel selbst untergliedert sich nochmals in einen problemunabhängigen und
problemabhängigen Teil. Die EALib-Bibliothek wird als Implementierung der problemunabhängigen Teile eines genetischen Algorithmus verstanden, und stellt in folge dessen ebenfalls lediglich diesen zur Verfügung. Dazu zählen u.a. die Selektions-,
Heirats-, und Ersetzungs-Schemata. Jegliche problemabhängige Module, wie konkrete Codierungen der Probleme/Genome, codierungs-abhängige Mutations- und
Crossover-Varianten werden im EAServer-Projekt zusammengefasst. Diese Bibliothek kapselt die im Rahmen dieser Diplomarbeit untersuchten Probleme. Für diese
problemabhängigen Module stellt die EALib-Bibliothek lediglich über Schnittstellen
den Rahmen zur Verfügung.
Die beiden anderen Module Bewertung und Steuerung sind jeweils problemunabhängig und somit in der EALib codiert. Die Aufgabe des Bewertungsmoduls stellt die
Feststellung der Tauglichkeit und Güte der einzelnen Individuen einer Generation
dar. Entsprechend der Konfiguration des Algorithmus wird ebenfalls eine Skalierung
der Fitness durchgeführt. Das Steuerungsmodul repräsentiert die Kontrolleinheit. Sie
kapselt die Konfiguration des Algorithmus, generiert Nachrichten für übergeordnete
Layer (EAServer) und errechnet und prüft die Abbruchbedingung des Algorithmus.
Durch diese Untergliederung in die oben genannten Komponenten ist es gelungen ei-
Abbildung 6.2.: Komponenten der EALib-Bibliothek
49
6 Server für evolutionäre Verfahren
ne software-technische Umsetzung eines genetischen Algorithmus zu finden, so dass
dieser modular aufgebaut und in Folge dessen stetig erweiterbar ist. Dieser Vorteil
schlägt sich ebenfalls in der Tatsache nieder, dass die EALib-Bibliothek nicht nur für
ein konkretes Problem entworfen wurde, sondern Untersuchungen unterschiedlicher
Problemfelder erlaubt.
6.2.2. Softwarearchitektur
Die im vorangegangenen Kapitel beschriebenen Komponenten der software-technischen Umsetzung eines genetischen Algorithmus sollen im Folgenden näher beleuchtet
werden. Um die verschiedenen evolutionären Strategien der einzelnen Evolutionsmechanismen zu modellieren wurde in allen drei Komponenten das Strategy-Pattern
verwendet. Es wird eine Familie von Algorithmen definiert, jede einzelne gekapselt
und somit austauschbar gemacht. Damit ist eine objekt-orientierte Umsetzung der
Strategien gelungen und es wird die Variation des Algorithmus unabhängig von den
ihn nutzenden Klienten ermöglicht. Schnittstellen bzw. abstrakte Klassen geben den
Rahmen des Evolutionsmechanismus vor; konkrete Implementierungen dieser Klassen codieren letztlich die entsprechende Variante des Mechanismus.
Dieses Muster wurde zur Konfiguration der Bibliothek gewählt, da damit auf einfache Art und Weise vollständige Erweiterbarkeit nicht nur der problemabhängigen,
sondern auch der problemunabhängigen Teile gewährleistet und somit einem der
Hauptziele des praktischen Teils der Diplomarbeit Rechnung getragen werden kann.
Kernel
Der Kernel der EALib-Bibliothek kapselt die problemunabhängigen Teile eines gesamten genetischen Kernels (vgl. Abbildung 6.3). Fassade dieses Moduls ist die Klasse EAPopulation. Sie repräsentiert die Kommunikationsschnittstelle zum Steuermodul. Von diesem erhält sie ein Konfigurationsobjekt für die Einstellung des evolutionären Laufs. Des Weiteren speichert sie sowohl die aktuelle, neue und vorangegangene Generation und legt die neue dem Steuerungsmodul vor. Alle Generationen
sind durch den Container vector<EAGenom*> der STL codiert.
Für die Erzeugung von Genomen/Codierungen wurde das Abstract Factory Pattern
verwendet (EAGenomFactory); es wird eine Schnittstelle zum Erzeugen von Familien verwandter oder voneinander abhängiger Objekte angeboten, ohne ihre konkreten
Klassen zu benennen. Die abstrakte Fabrik kreiert Genome/Individuen vom Typ
50
6.2 Bibliothek für evolutionäre Algorithmen
EAGenom. Eine konkrete Fabrik erzeugt folglich ein ihr zugehöriges Genom/Codierung4 . Dieses Pattern ermöglicht eine Erweiterbarkeit im Hinblick auf diverse
Codierungen der zu optimierenden bzw. lösenden Probleme. Soll ein neues Genom
eingeführt werden, so muss dieses die abstrakte Klasse EAGenom implementieren
und die zugehörige konkrete Fabrik codieren, indem die Schnittstelle EAGenomFactory implementiert wird.
Auf die Erzeugung der Genome folgt die Initialisierung dieser mit zufälligen Werten. Für eine Bewertung der Genome wird die Generation dem Bewertungsmodul
übergeben.
Nachdem die Klasse EAPopulation die bewertete Generation zurückerhalten hat,
Abbildung 6.3.: Klassendiagramm des problemunabhängigen Kernels
wird sie der Fassade des Reproduktionsteils übergeben, welche durch die Klasse
EAReplacement codiert wird. Diese abstrakte Klasse bildet eine Schnittstelle für verschiedene Ersetzungsschemata, wie dem Generational Replacement, Elitismus oder
weiteren Mechanismen, wie in Kapitel 3 erläutert. Grund für die Wahl der Klasse
4
Individuen dieser Genom-Klasse implementieren die abstrakte Klasse EAGenom
51
6 Server für evolutionäre Verfahren
EAReplacement als Fassade des Reproduktionsapparates ist die Tatsache, dass lediglich diese Information darüber besitzt und besitzen soll, wie viele Individuen neu
generiert werden müssen. So muss zum Beispiel bei einem Generational Replacement
eine komplette neue Generation erzeugt werden, wobei im Fall des Elitismus es genügt beispielsweise 90 Prozent der Populationsgröße neue Individuen zu generieren.
Würde eine extra Fassade eingeführt werden, und alle Reproduktionsschritte5 von
ihr gesteuert ausgeführt werden, so entsteht in einigen Varianten ein Overhead an
generierten Individuen, was wiederum in einem Ausführungszeitnachteil resultiert.
Um dies zu vermeiden wurde die Klasse EAReplacement als Fassade ausgewählt. Diese erzeugt, wie oben beschrieben, abhängig vom gewählten Ersetzungsschema eine
entsprechende Anzahl neuer Genome, indem sie die aktuelle Generation der Schnittstelle EAMating übergibt. EAMating ist die Schnittstelle der Familie der Heiratsalgorithmen und wählt über die Schnittstelle EASelection ein Individuum entsprechend
dem verwendeten Selektionsverfahren (i.d.R. Roulette Wheel/EARouletteWheel) aus.
Dieses Individuen wird abhängig vom Heiratsalgorithmus6 mit weiteren selektierten
Individuen durch Crossing-over kombiniert und anschließend mutiert. Nach Beendigung des Heiratsalgorithmus, kann das Ersetzungsschema neue und alte Individuen
vereinen. Die neu entstandene Generation wird der Klasse EAPopulation zurückgegeben.
Steuerungsmodul
Das Steuerungsmodul (vgl. Abbildung 6.4) erhält von der übergeordneten Schicht
die Konfiguration des Algorithmus. Eine Konfiguration besteht im Fall der EALibBibliothek aus einer Reihe von Zeigern auf die Implementierungen der Schnittstellen
bzw. abstrakten Klassen der einzelnen Strategien der Evolutionsmechanismen, sowie
Angaben über Abbruchkriterium und Populationsgröße. Die Algorithmuskonfiguration wird durch die Klasse EAConfig gekapselt.
Der Konfiguration des Algorithmus folgt die Initialisierung der Klasse EAPopulation
und anschließend der Start des evolutionären Laufs.
Ist eine neue Generation erzeugt worden, wird diese der Klasse EvolutionAlgorithm
vorgelegt, welche abhängig vom Abbruchkriterium entscheidet, ob fortgefahren werden soll. Ist das Abbruchkriterium nicht erfüllt, werden statistische Informationen,
5
6
Selektion, Heirat, Ersetzung
EALib codiert durch die Klasse EARandomMating das zufällige Verheiraten
52
6.2 Bibliothek für evolutionäre Algorithmen
welche die Klasse EAPopulation bereitstellt gesammelt und durch die Statistik-Klasse
EAStatistic gekapselt. Diese wird als Statistik-Nachricht 7 (Klasse: EAStatisticMessage) mittels des im Kapitel 6.5.1 beschriebenen Kommunikations-Mechanismus an
höhere Schichten übertragen. Die abgeschlossene Abarbeitung einer Generation wird
durch eine Generations-Nachricht (Klasse: EAGenerationMessage) signalisiert. Wird
der evolutionäre Lauf nicht fortgesetzt – das Abbruchkriterium ist erfüllt, so wird
eine Ende-Nachricht (Klasse EAFinishMessage) gesendet und der evolutionäre Lauf
beendet. Tritt ein Fehler in der Bibliothek auf, so wird eine Ausnahme geworfen,
welche bis zur Fassade des evolutionären Algorithmus EvolutionAlgorithm weitergereicht und dort gefangen wird. Eine Fehler-Nachricht (Klasse: EAErrorMessage) wird
erzeugt, welche Informationen über die Art des Fehlers enthält, und gesendet. Die
Nachrichtenklassen, EAStatisticMessage, EAGenerationMessage, EAFinishMessage und
EAErrorMessage implementieren die Schnittstelle EAMessage. Mittels einer Nachrichtenwarteschlange, welche durch den Container queue<EAMessage*> der STL realisiert wird, können übergeordnete Schichten auf einzelne Nachrichten zugreifen und
entsprechend reagieren.
Grund für die Umsetzung der Nachrichten als Klassen und nicht beispielsweise als
Zeichenkette ist, dass auf diese Weise zusätzliche Informationen zu den eigentlichen Nachrichten selbst mit übertragen werden können. Für eine Erweiterbarkeit
der Nachrichten ist auch hier das Strategy-Pattern zum Einsatz gekommen.
Zur Kapselung mehrerer Populationen wird ebenfalls auf die STL zurückgegriffen.
Ein vector<EAPopulation*> enthält Zeiger auf eine bestimmte Anzahl von Populationen. Dadurch wird es möglich eine Evolution von Population zu simulieren. Die
für einen erheblichen Geschwindigkeitsvorteil nötige Parallelisierung der Populationenevolution wurde nicht implementiert, da dieser Mechanismus den Rahmen der
Diplomarbeit gesprengt hätte. Im Falle der EALib-Bibliothek ist die Evolution von
Population als rein serieller Prozess verwirklicht worden. Es finden sich eine Implementierung des Insel-8 und Netzwerk-Modells9 in den Bibliotheken. Das NetzwerkModell wurde als eine ringförmige Anordnung von Populationen aufgebaut, da ein
synchroner Informationsaustausch erfolgt; Informationen/Individuen werden zu definierten Zeitpunkten jeweils zyklisch durch den Ring geschoben.
7
die zu übertragenen Nachrichten sind software-technisch als Objekte umgesetzt
vgl. Kapitel 5.1
9
vgl. Kapitel 5.2
8
53
6 Server für evolutionäre Verfahren
Abbildung 6.4.: Klassendiagramm des Steuerungsmoduls
Bewertungsmodul
Dem Bewertungsmodul (vgl. Abbildung 6.5) werden Genome/Codierungen zur Feststellung der Tauglichkeit und Güte vorgelegt. Fassade dieses Moduls ist die Klasse
EAEvaluation, welche die Koordination der beiden Mechanismen – Bewertung und
Skalierung – übernimmt. Da die Bewertung eine problemabhängige Funktion darstellt, müssen konkrete Bewertungen die Schnittstelle EAObjective implementieren,
um auf diese Weise in den Algorithmus eingefügt werden. Die Skalierung wird durch
die Schnittstelle EAScaling repräsentiert; spezielle Skalierungsmechanismen implementieren diese10 .
Die Unterklassen der Schnittstelle EAObjective ermitteln die Bewertung der jeweiligen Codierung, während jene der Schnittstelle EAScaling mittels diversen Skalierungsmechanismen einen Fitnesswert errechnen. Die bewertete Generation wird für
eine weitere Bearbeitung dem Kernel zurückgegeben.
10
EANoScaling, EALinearScaling, usw.
54
6.3 Server-Bibliothek
Abbildung 6.5.: Klassendiagramm des problemunabhängigen Bewertungsmoduls
6.3. Server-Bibliothek
6.3.1. Exkurs: Java Native Interface
Die Programmiersprache Java ist genau genommen keine plattformunabhängige
Sprache, da sie zum einen eine Virtual Machine benötigt, welche für die jeweilige
Systemarchitektur übersetzt werden muss, und zum anderen auf keine Systemresourcen eines Rechners zugreifen kann. Hierzu ruft Java native Methoden auf, die nicht
in Java implementiert sind. Diese Schnittstelle zwischen Java und einer konkreten
Plattform wird durch das Java Native Interface (JNI) definiert. Mit Hilfe des JNI
können aus der Java Virtual Machine (JVM) heraus plattformspezifische Funktionen verwendet werden. Über die so genannte Invocation-API kann beispielsweise ein
C-Programm auf Java-Programme zugreifen. Mit diesen beiden Teilen kann eine Migration eines Altsystems nach Java realisiert werden. Mögliche Teile eines Projekts,
wie die grafische Benutzeroberfläche, werden in Java programmiert, und die übrigen
Teile in einer plattformabhängigen Sprache. Jedoch bedarf diese Realisierung einen
Wrapper, welcher über die plattformabhängigen Teile gelegt werden muss. Damit
wäre die Applikation lauffähig.
Liegt Programmcode in einer anderen Programmiersprache vor, dann muss dieser
zu einer dynamisch ladbaren Bibliothek gebunden werden. Diese Bibliothek implementiert die nativen Methoden, hält sich jedoch an spezielle Namenskonventionen.
Das bedingt, dass es nicht möglich ist, beliebige Bibliotheken in Java einzubinden,
die auf dem System schon vorhanden sind. Es lässt sich z.B. unter Windows nicht
55
6 Server für evolutionäre Verfahren
die Bibliothek twain.dll verwenden, um Scanner anzusteuern.
Die dynamisch ladbaren Bibliotheken sind unter Windows Dynamic Linked Libraries und unter Unix Shared Objects. Ist eine dynamische Bibliothek vorhanden, muss
sie in Java eingebunden werden. Dazu existiert die Methode System.loadLibrary(),
welche die Bibliothek zur Laufzeit in die JVM einbindet. Jeder Aufruf der nativen
Funktion wird an die C-Funktion weitergeleitet.
Da aus Effizienzgründen der genetische Algorithmus in C++ implementiert wurde,
jedoch eine GUI-Programmierung mit derselbigen ein plattformunabhängiges Framework wie Qt bedurft hätte, dieses aber erst ab Version 4 eine GUI-Entwicklung für
Windows unter der GPL zulässt, wurde auf Java unter zur Hilfenahme des SwingFrameworks zurückgegriffen.
Dieses ermöglichte eine Migration der Projekte EALib, EAServer und EAServerUI.
6.3.2. Exkurs: POSIX Threads
In Shared-Memory Multiprozessorarchitekturen können Threads zur Realisierung
von Parallelität genutzt werden. In der Vergangenheit haben Hardwarehersteller ihre eigenen proprietären Threadversionen implementiert. Diese Implementierungen
unterschieden sich substantiell voneinander und machten es schwierig für Softwareentwickler portable Thread-Applikationen zu schreiben. Es war eine standardisierte Programmierschnittstelle nötig, um alle Möglichkeiten der Threads zu nutzen.
Für Unix-Systeme wurde die Schnittstelle durch den IEEE POSIX 1003.1c Standard (1995) spezifiziert. Implementierungen, welche sich an diesen Standard halten,
werden als POSIX Threads oder PThreads bezeichnet. Die meisten Hardwarehersteller bieten heutzutage zusätzlich zu ihren proprietären APIs POSIX Threads an.
PThreads sind als eine Anzahl von Typen und Prozeduren der Programmiersprache
C definiert. Für eine Implementierung wird lediglich eine pthread.h Header-Datei und
Thread-Bibliothek benötigt, welche für unterschiedliche Systemarchitekturen verfügbar ist und somit eine plattformunabhängige Entwicklung ermöglicht11 . Aufgrund
der an das zu entwickelnde System gestellten Anforderung der Plattformunabhängigkeit wird für die Realisierung von Nebenläufigkeit in der Server-Bibliothek auf
POSIX-Threads zurückgegriffen.
11
Siehe für eine Win32 Systemarchitektur: [PTH]
56
6.3 Server-Bibliothek
6.3.3. Exkurs: Netzwerk Programmierung und
Cross-Plattform Entwicklung
Netzwerk Programmierung
Ein Socket ist eine bidirektionale (Vollduplex) Software-Struktur, welche zur Netzwerkoder Interprozess-Kommunikation verwendet wird. Somit ist ein Socket eine Schnittstelle zwischen einem Prozess und einem Transportprotokoll. In den RFC12 ist ein
Socket als ein 5-Tupel aus Ziel- und Quell-IP-Adresse, Ziel- und Quell-Port und dem
Netzwerkprotokoll beschrieben. Sockets werden in UDP und TCP verwendet. Seit
1983 verwendet BSD die Netzwerk-Sockets in seiner Berkley-Socket API. Ebenso Linux, Solaris und viele andere Unix-Systeme verwenden die BSD-Sockets. Der Zugriff
erfolgt ähnlich wie auf Dateien mit einem (File-)Deskriptor; einziger Unterschied:
es handelt sich hier um Kommunikationskanäle. Microsoft Windows verwendet eine
ähnliche API wie jene von den Berkley-Sockets, den Windows-Sockets (kurz: Winsock).
Cross-Plattform Entwicklung
Die für den Evolution Algorithm Server entwickelte Bibliothek (SocketCPI ) zur
Bereitstellung der Netzwerkfunktionalität für Windows- und Unix-artige Systeme
zeigt einen einfachen Weg, wie mittels #ifdef Präprozessoranweisungen eine CrossPlattform Bibliothek/Anwendung geschrieben werden kann. Problem hierbei ist,
das alles in eine Datei geschrieben wird. Für kleinere Projekte – wie der SocketCPI Bibliothek – ist dies zwar dennoch möglich, jedoch für umfangreichere Programme empfiehlt es sich, einen abstrakten Layer zu entwerfen. Der Abstraktions-Layer
isoliert Plattform-spezifische Funktionen und Datentypen in separate Module für
portablen Code. Die Plattform-spezifischen Module werden dann speziell für jede
Plattform geschrieben. Des Weiteren wird eine Header-Datei erstellt, in denen sich
die Plattform-spezifischen typedef’s und #define’s samt Funktionsprototypen der
Module befinden. Bei einer Anwendung selbst wird dann lediglich diese HeaderDatei eingebunden. Im Falle der SocketCPI -Bibliothek wurde jedoch auf diesen
Layer unter Abwägung des Nutzens verzichtet, da sich die plattform-spezifischen
Netzwerkfunktionen auf einige wenige Systemfunktionen reduzieren ließen.
12
Requst for Comments; Reihe von technischen und organisatorischen Dokumenten zum Internet;
wurde 1969 begonnen
57
6 Server für evolutionäre Verfahren
6.3.4. Komponenten
Das Teilprojekt EAServer besteht aus drei wesentlichen Komponenten (vgl. Abbildung 6.6):
Die problemabhängige Komponente des evolutionären Algorithmus selbst untergliedert sich nochmals in den problemabhängigen Teil des Kernels und Bewertungsmoduls. Dort sind die im Rahmen der Diplomarbeit untersuchten Probleme nebst ihren
genetischen Operatoren, wie Mutation und Crossover, und Bewertung zusammengefasst.
Wie einleitend beschrieben, ist ein Teil der Funktionalität der Server-Bibliothek die
Kommunikation mit diversen Clients. Hierfür wurde ein eigenes Kommunikationsprotokoll entworfen, welches in Kapitel 6.3.5 beschrieben wird. Das Kommunikationsmodul wurde modelliert, so dass unabhängig von der zugrunde liegenden Kommunikationstechnologie eine Verbindung zu einem entsprechenden Klienten aufgebaut
werden kann. Es muss lediglich für die entsprechende Technologie eine Kommunikationsklasse geschrieben werden. Im Rahmen der Diplomarbeit wurde die im Kapitel
6.3.3 beschriebene SocketCPI -Bibliothek für die Realisierung der Netzwerkkommunikation eingebunden. Auf weitere Übertragungstechnologien wurde auf Grund des
Umfangs und Nutzens verzichtet.
Das Wrappermodul nutzt im Wesentlichen das Java Native Interface zur Kommunikation mit einer Benutzerschnittstelle. Kommandos werden über das JNI in den
Server und mittels der Invocation-API aus dem Server für z.B. eine Visualisierung
übertragen (vgl. Kapitel 6.5.1). Durch die Ausgliederung einer GUI ist eine Trennung
zwischen Darstellung und Daten im wahrsten Sinne des Wortes vollzogen worden. Es
wäre daher denkbar den Server auf eine Weise zu erweitern, dass dieser als Prozess
seine genetischen Dienste gänzlich über Netzwerk anbietet.
Das Kommunikationsmodul erlaubt bereits die Anbindung von Klienten z.B. für eine Visualisierung eines Chromosoms. Es ist zusammen mit der Tatsache, dass der
Server um verschiedene Kommunikationstechnologien erweitert werden kann, deshalb auch vorstellbar, mittels dieses Servers reale Objekt, wie z.B. einen mobilen
Roboter, zu steuern.
Nachteilig an diesem Design ist jedoch, dass die problemabhängigen Komponenten
des genetischen Algorithmus mit in die Server-Bibliothek aufgenommen wurden.
Diese sollten in einer eigenen Bibliothek ausgelagert werden, so dass die strikte
Trennung zwischen Algorithmus und Anwendung auch hier vollzogen ist.
58
6.3 Server-Bibliothek
Abbildung 6.6.: Komponenten des EAServer-Pakets
6.3.5. Kommunikationsprotokoll
Es besteht die Möglichkeit, Clients mit der EAServer-Bibliothek zu verbinden. Hierfür wurde ein Kommunikationsprotokoll entwickelt, welches unabhängig von der zu
Grunde liegenden Technologie den Transfer der entsprechend benötigten Daten gewährleistet. Verbindet sich ein Client zum Server, so startet dieser unmittelbar seinen
Idle-Thread, welcher sich blockiert und auf Nachricht vom Client wartet.
Möchte der Client die Verbindung beenden, so sendet er eine BYE-Nachricht, welche
bewirkt, dass der Server den Idle-Modus verlässt und anschließend die Verbindung
trennt.
Wünscht der Server die Verbindung zu beenden, so muss dieser dem Client eine
BYE-Nachricht senden, damit jener dem Server die Nachricht mit einer weiteren
BYE-Nachricht bestätigt, so dass wieder der Idle-Modus verlassen und die Verbindung getrennt werden kann.
Sollen Daten beispielsweise zur Bewertung eines Individuums zwischen Client und
Server gesendet werden, so veranlasst der Server mittels des Aufrufs der Dienstfunktion setIdle(false) den Server den Idle-Modus zu verlassen. Diese Funktion resultiert
nun im selbigen oben beschriebenen Mechanismus. Der Server sendet dem Client
eine WAKEUP-Nachricht, welche mit derselbigen bestätigt wird. Nun können Daten
zwischen dem Client und Server ausgetauscht werden. Diese werden ebenfalls mit
59
6 Server für evolutionäre Verfahren
einer ACK-Nachricht bestätigt. Nach Abschluss der zu sendenden Daten wird der
Idle-Modus wieder mittels des Funktionsaufrufes setIdle(true) betreten.
Abbildung 6.3.5 zeigt das hier beschriebene Protokoll nochmals im Bild. Dieses
Abbildung 6.7.: Kommunikationsprotokoll der Server-Bibliothek
Kommunikationsprotokoll wurde auf Grund der verwendeten Technologien notwendig. Eine nähere Erklärung hierzu ist in Kapitel 6.5.2 gegeben.
6.3.6. Softwarearchitektur
Die Architektur der Server-Bibliothek (vgl. Abbildung A.2) besteht aus vier Komponenten. Diese werden im Folgenden näher beschrieben. Hier wurde ebenfalls für die
Realisierung einer Erweiterbarkeit der Bibliothek auf das Strategy-Pattern zurückgegriffen. Konkrete evolutionäre Mechanismen werden mittels Schnittstellen zusammengefasst, so bei den diversen Mutations- und Crossover-Strategien der einzelnen
konkreten Genome, wie auch im Kommunikationsmodul.
Problemabhängiger Kernel
Für die Modellierung eines neuen Problems, welches mittels der EALib-Bibliothek
gelöst bzw. optimiert werden soll, muss die abstrakte Fabrik EAGenomFactory implementiert werden. Diese konkrete Fabrik erzeugt einen Zeiger auf das konkrete
60
6.3 Server-Bibliothek
Problem, welche seinerseits die abstrakte Klasse EAGenom implementiert (vgl. Kapitel 6.2.2). Im Rahmen dieser Diplomarbeit wurden folgende Probleme untersucht:
1. Approximation einer natürlichen Zahl (EANumberGenom)
2. Automatische Formelgenerierung (EAFunctionGenom)
3. Steuerungsaufgaben eines Fahrzeugs (EACarGenom und EAVehicleGenom)
Für jedes der einzelnen Problemfelder wurde ein konkretes Genom modelliert, welches eine dem Problem entsprechende Codierungsform beinhaltet. Crossing-overund Mutationsstrategien13 sind unter Verwendung des Strategy-Patterns über Schnittstellen zusammengefasst, welche in Abhängigkeit zu den entsprechenden konkreten Genomen stehen. Im Folgenden sind diese Chromosomen nebst Mutations- und
Crossing-over-Schemata im Hinblick auf die software-technischen Hintergründe näher beschrieben. Weitere theoretische Überlegungen, sowie Auswertungen hierzu
sind in Kapitel 11 zu finden.
Chromosom: vector<bool> Für die Approximation einer natürlichen Zahl wurde auf einen Boolschen-Vektor aus der STL zurückgegriffen (vector<bool>). Abhängig von der Konfiguration des evolutionären Algorithmus kann dieser als Standardbinär- oder Gray-Code interpretiert und entsprechend dekodiert werden. Der genetische Algorithmus muss die einzelnen Werte des Vektors so bestimmen, dass die
gewünschte Zahl möglichst gut approximiert ist. Die Crossing-over und Mutationsverfahren sind dem Kapitel 3 entsprechend implementiert worden: One-Point-, TwoPoint-Crossing-Over und Zufallsschablone, sowie gleichverteilte, normalverteilte und
positionsabhängige Mutation.
Chromosom: EA2DoubleChrom Die Automatische Formelgenerierung wird durch
die Approximation von Polynomen realisiert, weshalb eine Codierung in Form eines Arrays bestehend aus einer Struktur von zwei Double-Werten gewählt wurde
(EA2DoubleChrom). In diesem Ansatz wird versucht durch Polynome n-ten Grades
zu approximieren. Der zu approximierenden Funktion wird ein Polynom der Form
y = a1 ∗ xb1 + a2 ∗ xb2 + . . . + an ∗ xbn
13
(6.1)
vgl. Kapitel 3
61
6 Server für evolutionäre Verfahren
gegenübergestellt. Hier muss der Algorithmus die Parameter a – 1. Parameter der
Struktur – und b – 2. Parameter der Struktur – des Polynoms so bestimmen, dass
die gewünschte Funktion möglichst gut approximiert ist. Diese Codierungsform bedarf eine Abänderung der Standard-Crossing-over und Mutationsverfahren, da diese
sich lediglich auf binär-codierte Genotypen beziehen. Im Fall der automatischen
Formelgenerierung, entspricht der Invertierung einzelner Bits im Fall der Mutation
die Addition eines Wertes im Intervall [−1; 1]. Für die restlichen Mechanismen der
Mutation – gleichverteilt, normalverteilt und positionsabhängig – sind keine Änderungen der Standard-Schemata notwendig. Die Crossing-over Verfahren können
analog zu der Theorie entsprechend dem Kapitel 3 übernommen werden, da sich
diese auf Vektorpositionen beziehen. Hierbei werden die Parameter a und b jeweils
nur zusammen und nicht einzelnen getauscht.
Im Fall der Optimierung der Steuerungsaufgaben eines simulativen Kraftfahrzeugs
wurden zwei verschiedene Codierungsformen implementiert.
Chromosom: EAArithmeticChrom Der arithmetische Baum EAArithmeticChrom
ist aus verschiedenen unären und binären mathematischen Grundoperationen, Parameter und Konstanten aufgebaut (vgl. Abbildung 6.8). Seine Architektur (vgl.
Abbildung 6.8.: Arithmetischer Baum
Abbildung A.2) besteht aus einer generischen Basisklasse EATree, die jegliche Grund-
62
6.3 Server-Bibliothek
funktionalitäten eines Baumes beinhaltet. Der Vorlageparameter der konkreten Implementierung der Klasse EAArithmeticChrom ist die Klasse EAArithmeticData, welche die oben erwähnten Funktionen, Parameter und Konstanten beherbergt. Diese
Parameterwerte definieren ein Element entweder als Blatt oder Knoten. Ein Knoten
besteht immer aus einer mathematischen Funktionen, ein Blatt aus einem Parameter
bzw. einer Konstante. Abhängig ob die mathematische Operation unär oder binär
ist, enthält der jeweilige Knoten entweder einen oder zwei nachfolgende Elemente.
Die Klasse EAArithmeticChrom ist sowohl Wurzel als auch Element des Baumes.
Aus seinen Blättern und Knoten berechnet der Baum sich selbst in Abhängigkeit
von den Parametern zu einem Wert reeller Größe, der als Lenkeinschlag interpretiert
wird. Dieser wird in der Simulation zur Steuerung des Fahrzeugs verwendet. Ziel hier
ist es einen Baum im Suchraum zu finden, welcher abhängig von den Parametern
Lenkeinschläge errechnet, die ein Fahrzeug die ihm zugedachte Steuerungsaufgabe
möglichst gut ausführen lässt.
Mutations- und Crossing-over Schemata sind in diesem Fall anders aufgebaut als
Abbildung 6.9.: Arithmetischer Baum: Crossing-Over
63
6 Server für evolutionäre Verfahren
die bisher beschriebenen. Als einzige Crossing-over Strategie ist das One-PointCrossover implementiert worden, da eine Implementierung der weiteren Verfahren
– Two-Point-Crossover und Zufallsschablone – im Hinblick auf ihren Nutzen nicht
zweckmäßig erschien. Das One-Point Crossover ist hier so gestaltet, dass per Zufall
jeweils ein Knoten der beiden Eltern ausgewählt wird, und die so selektierten Teilbäume getauscht werden und auf diese Weise zwei neue Chromosomen – Kinder –
entstehen (vgl. Abbildung 6.9). Bei den Mutationsschemata wird mit gleichverteilter bzw. normalverteilter Wahrscheinlichkeit ein Knoten des Chromosomenbaumes
selektiert, der Unterbaum gelöscht und an dessen Stelle ein neuer Baum generiert
und eingehängt (vgl. Abbildung 6.10). Auf die Implementierung einer positionsabhängigen Variante der Mutation wurde im Hinblick auf Ihren Nutzen verzichtet.
Abbildung 6.10.: Arithmetischer Baum: Mutation
Chromosom: vector<double> Als Alternative zu diesem arithmetischen Baum
wurde eine weniger rechenintensive Variante gewählt. Ein 1-dimensionaler Vektor
aus Double-Werten (vector<double>) codiert die für die Simulation nötigen Lenkeinschläge. Ziel ist hier ebenfalls einen möglichst guten Vektor im Verlauf der Evolution zu finden, um ein Fahrzeug eine Aufgabe lösen zu lassen.
Die Mutations- bzw. Crossing-over-Verfahren entsprechen jenen im Paragraphen
Chromosom: EA2DoubleVektor beschriebenen. Der einzige Unterschied besteht darin, dass es sich nicht um einen Vektor einer Struktur, sondern von Double-Werten
handelt. Dieses Faktum schlägt sich aber lediglich in der Tatsache nieder, dass bei
den Kreuzungsstrategien nur einzelne Werte und nicht Wertpaare getauscht werden.
64
6.3 Server-Bibliothek
Abbildung 6.11.: Klassendiagram des problemabhängigen Bewertungsmoduls
Problemabhängiges Bewertungsmodul
Das problemabhängige Bewertungsmodul (vgl. Abbildung 6.11) kapselt die Prüfung
der Tauglichkeit der Chromosomen einer Generation. Für jedes der oben beschriebenen konkreten Genome existiert eine Klasse, welche diese Bewertung übernimmt,
z.B. EANumberObjective. Diese Klassen implementieren die Schnittstelle EAObjective
des problemunabhängigen Bewertungsmoduls der Bibliothek für evolutionäre Verfahren EALib (s. Abbildung 6.11). Eine Erläuterung der theoretischen Hintergründe
der jeweiligen Bewertung der Individuen wird in Kapitel 11 gegeben.
Wrappermodul
Für das Wrappermodul (vgl. Abbildung 6.12) wurde auf das Java-Native-Interface
und die Invocation-API von Java zurückgegriffen. Die Klasse EAWrapper bildet die
Verknüpfung der Technologien C++ und Java und somit die Schnittstelle zwischen
Server und User Interface. Jegliche Kommunikation in die Bibliothek, sowie aus der
Bibliothek geschieht über ihr. Beim Starten des Algorithmus aus der GUI werden
Informationen in die EAServer-Bibliothek übergeben, welche dort ausgewertet und
verarbeitet werden. Die Nachrichten der in Kapitel 6.5.1 erläuterten nachrichtenorientierten Kommunikation der EALib-Bibliothek werden ebenfalls von diesem Objekt aufgenommen und an die Benutzerschnittstelle weitergegeben, so dass eine entsprechende Visualisierung erfolgen kann.
Die Klasse EAWrapper steht in Abhängigkeit mit der Schnittstelle WorkerThread.
Dieses Objekt kapselt die Technologie der POSIX-Thread-Funktionalität. Die Unterklasse EAWorkerThread wird von EAWrapper dazu genutzt, den Algorithmus in
einem eigenen Thread auszuführen, um ein Dispatching Nachrichten zu ermöglichen
65
6 Server für evolutionäre Verfahren
(vgl. Kapitel 6.5.1).
Abbildung 6.12.: Klassendiagramm des Wrappermoduls
Kommunikationsmodul
Der Server soll Clients ermöglichen, evolutionäre Algorithmen zu verwenden. Hierfür
ist eine Kommunikation zwischen Server und Client nötig, welche nach den in Kapitel
6.3.5 dargestellten Kommunikationsprotokoll verläuft. Die Architektur des Kommunikationsmoduls (vgl. Abbildung 6.13) wurde so geschaffen, dass es nicht zwingend
erforderlich ist, dass ein Klient ebenfalls eine über TCP ansprechbare Applikation
darstellen muss. Es ist möglich, verschiedene Übertragungstechnologien einzusetzen.
Zentrale Klasse dieses Moduls ist die abstrakte Klasse EAConnection. Sie beinhaltet neben Schnittstellenfunktionen einer Kommunikationsverbindung zwischen Client und Server, einen nachrichten-orientierten Mechanismus zur Kommunikation
mit übergeordneten Layern. Dieser Kommunikationsweg entspricht dem der EALibBibliothek. Die generische Klasse queue<EAConnectionMessage*> der STL codiert
wieder eine Nachrichtenwarteschlange. Die Verbindungsnachrichten werden durch
die Klasse EAConnectionMessage zusammengefasst, welche Aufschluss über den Verbindungsstatus geben. Eine genaue Erläuterung der Funktionsweise ist in Kapitel
6.5.1 zu finden.
Von der Kommunikationstechnologie abhängige Klassen (z.B. EATCPSocket) implementieren die Basisklasse EAConnection. Diese konkreten Objekte realisieren letzt-
66
6.4 Server User-Interface
lich das Kommunikationsprotokoll und setzen es auf die unterlagerte Kommunikationstechnologie um.
Aufgrund dieses Designs des Kommunikationsmoduls wäre es auch denkbar, eine
Klasse für eine drahtlose Kommunikation zu schreiben. Diese implementiert die abstrakte Klasse EAConnection, sowie das Netzwerkprotokoll. Ein Klient, in diesem
Fall z.B. ein mobiler Roboter, könnte somit auch die evolutionären Algorithmen des
Servers nutzen.
Im Fall der EAServer-Bibliothek wurde ein EAFunctionServer und EACarServer geschrieben. Beide stellen aus Sicht des Algorithmus eine Fassade dar, welche hinter
sich den Kommunikationsapparat zum Klienten verbergen. Der EAFunctionServer
kann für eine Applikation zur Visualisierung einer Funktion verwendet werden. Er
ist vom eigentlich evolutionären Lauf ausgeschlossen und auch nicht nötig, da im Fall
der Approximation einer Funktion die Bewertung der Individuen keine Visualisierung des Problems benötigt. Das Problem der Optimierung der Fahrzeugsteuerung
bedarf jedoch der Klasse EACarServer. Sie muss in den evolutionären Lauf mit eingebunden werden, denn die Bewertung eines Fahrers kann im Gegensatz zum Vergleich
einer Soll mit einer Ist-Funktion nicht ohne einer externen Fahrzeugsimulation geschehen, welche in Kapitel 7 näher beschrieben wird.
6.4. Server User-Interface
6.4.1. Exkurs: Grafikprogrammierung unter Java
Abstract-Window-Toolkit und Java Foundation Classes
Eine Programmiersprache, welche plattformunabhängige Softwareentwicklung unterstützt, muss für die Gestaltung grafischer Oberflächen eine entsprechende Bibliothek anbieten. Eine solche muss grafische Primitivoperationen realisieren, grafische
Interaktionskomponenten unterstützen und ein Modell zur Behandlung von Ereignissen definieren.
Da Java-Programme portabel sein müssen, ergibt sich das Problem, dass eine Komponente beispielsweise von einer bestimmten Plattform nicht unterstützt wird und
ein anderes Feature wiederum nicht von einer anderen. Aus diesem Grund kann die
Bibliothek nur das aufnehmen, was definitiv von jeder grafischen Oberfläche unterstützt wird. Java definiert hierzu das Abstract-Window-Toolkit (kurz: AWT), das
67
6 Server für evolutionäre Verfahren
Abbildung 6.13.: Klassendiagramm des Kommunikationsmoduls
konkrete Plattformen wie Microsofts Windows, Apples MacOS oder Unix mit Motif
implementieren. Auf diese Weise wird jede Komponente in Java auf eine Komponente
der Plattform abgebildet und integrieren sich somit in das jeweilige Look-And-Feel.
Nach der Freigabe des ersten AWTs zeigte sich jedoch, dass das Leistungsangebot nicht zukunftssicher gestaltet ist. Es sind Erweiterungen unter dem Name Java
Foundation Classes (kurz: JFC) zusammengefasst und in Java eingeführt worden14 .
Unter Verwendung dieses Swing-Frameworks wurde eine Oberfläche für die ServerBibliothek gestaltet und realisiert.
Ereignisse
Beim Arbeiten mit grafischen Oberflächen interagiert der Benutzer mit Komponenten. Das grafische System beobachtet die Aktionen der Benutzer und informiert die
Applikation über die angefallenen Ereignisse. Dann kann das laufende Programm
entsprechend reagieren.
14
Swing-GUI Komponenten, Pluggable Look-And-Feel, Accessibility, Drag-And-Drop
68
6.4 Server User-Interface
Die ausgesandten Botschaften werden in Ereignis-Klassen kategorisiert. Da es unterschiedliche Ereignisse gibt, kann das System somit die Ereignisse unterteilen und
eine Vorauswahl treffen. Alle Ereignisse der grafischen Oberfläche sind Objekte, die
aus einer Unterklasse von AWTEvent gebildet sind.
Listener
Im Ereignismodell von Java gibt es eine Reihe von Ereignisauslösern. Die Ereignisse
können sowohl von der grafischen Oberfläche als auch von eigenen Auslösern resultieren. Es existiert eine Reihe von Interessenten (Event-Handler), welche informiert
werden möchten, wenn ein Ereignis aufgetreten ist. Der Handler ist allerdings in
der Regel nicht an allen ausgelösten Ereignissen interessiert. Daher meldet er sich
bei einer Ereignisquelle an und diese informiert ihn, wenn ein Ereignis ausgesendet
wurde. Da der Interessent an der Quelle horcht, wird er auch Listener genannt. Es
existiert für jedes Ereignis ein eigener Listener, an den das Ereignis weitergeleitet
wird15 .
AWT, Swing und Threads
Beim AWT und bei Swing gibt es einen Thread, welcher für die Oberflächenelemente verantwortlich ist: den AWT-Thread. Er läuft parallel zum Hauptprogramm
und führt den Programmcode in den Listenern aus. Aus diesem Grund ist es ungünstig, in einen Event-Handler langen Programmcode zu legen, denn dann steht
die grafische Applikation und kann nicht weiter mit dem Benutzer interagieren. Der
AWT-Thread wäre blockiert. Wenn eine Aktion in einem Event-Handler ausgeführt
werden muss, dann sollte diese in einen separaten Thread starten, damit die grafische Oberfläche sofort wieder reaktionsfähig ist.
Das AWT ist Thread-sicher, da AWT auf Plattform-Peer-Elemente aufbaut. In einer
List-Box unter dem AWT beispielsweise ist es problemlos möglich, ein Element einzufügen und parallel zu löschen. Aus zwei Gründen wurde auf die Synchronisation
bei Swing jedoch verzichtet: zum einen können Operationen innerhalb von Threads
zu Deadlock-Situationen führen und zum anderen der Gewinn von Ausführungsgeschwindigkeit.
15
Delegation Model
69
6 Server für evolutionäre Verfahren
6.4.2. Komponenten
Die Benutzerschnittstelle setzt auf die EAServer-Bibliothek auf. Sie ermöglicht Benutzern eine Konfiguration der Bibliothek, sowie die Auswertung der Ergebnisse
eines evolutionären Laufs. Gegliedert ist die Java-Applikation in drei Komponenten:
Algorithmusmodul, Kommunikationsmodul und Visualisierungsmodul (vgl. Abbildung 6.14).
Das Algorithmusmodul ist das Abbild der für die Einstellung des genetischen Algo-
Abbildung 6.14.: Komponenten des EAServerUI-Pakets
rithmus notwendigen Klassen in Java. Diese werden durch einen Benutzer konfiguriert über das unterlagerte Java-Native-Interface in die EAServer-Bibliothek gegeben, wo sie verarbeitet und zur entsprechenden Ausführung des Algorithmus führen.
Das Kommunikationsmodul beinhaltet alle Klassen für die Einstellung der ServerFunktionalität der EAServer-Bibliothek. Sie werden ebenfalls wieder mittels der
nativen Schnittstelle in Java in die C++-Bibliothek übergeben, so dass dort eine
Verbindung zu einem Klienten geöffnet bzw. geschlossen werden kann.
Beide Module - Kommunikations- und Algorithmusmodul - bedienen sich hierbei
demselben Mechanismus, um Informationen aus der Bibliothek dem Benutzer sichtbar zu machen. Sie registrieren beide eine Callback-Funktion, welche mittels der
Invocation-API vom Wrappermodul bzw. Kommunikationsmodul der EAServerBibliothek aufgerufen wird. Die letztliche Visualisierung übernimmt hierbei das Visualisierungsmodul (vgl. Kapitel 6.5.1).
Dieses kapselt einen Dispatcher, welcher die Bibliotheksereignisse/-nachrichten an
die registrierten Handler weiterreicht, so dass über diese eine Darstellung der Infor-
70
6.4 Server User-Interface
mation erfolgen kann. Neben dieser Aufgabe kümmert sich das Visualisierungsmodul
ebenfalls um die benutzerfreundliche Konfiguration des Algorithmus, die Darstellung
des evolutionären Laufs, sowie die Aufbereitung der gesammelten statistischen Daten für eine an die Ausführung des Algorithmus anschließende Auswertung, um eine
Bewertung dessen vorzunehmen. Ebenfalls wurde ein Projektmanagement in das Visualisierungsmodul integriert. Es ermöglicht Projekte anzulegen, zu verwalten und
Daten eines Laufs zu speichern.
Darüber hinaus enthält das Visualisierungsmodul sämtlich für eine objektorientierte Visualisierung notwendigen Klassen für Darstellungskomponenten, wie Dialoge,
Frames, etc.
6.4.3. Parser
Die GUI ermöglicht eine Konfiguration des genetischen Algorithmus in seiner Gesamtheit. Dazu zählt auch die Konfiguration der Bewertung. Beispielsweise soll die
Möglichkeit gegeben sein, nicht nur eine Funktion sondern mehrere verschiedene
Funktionen zu approximieren. Aus diesem Grund wurde eine definierte Skriptsprache entwickelt, welche es dem Benutzer ermöglicht Parameter zu setzen und auf diese
Weise für die Bewertung wichtige Punkte zu konfigurieren. Es wurde ein Scanner
geschrieben, welcher die Symbole der Sprache ermittelt. Diese werden einem Parser
übergeben, der sie entsprechend den in Abbildung 6.15 dargestellten Regeln überprüft. Bei Richtigkeit wird die Konfiguration des Algorithmus geändert16 .
Das Schlüsselwort problem gibt an, welches Problemfeld aktuell zu optimieren ist.
Abhängig von diesem müssen zusätzliche Parameter definiert werden.
Approximation einer natürlichen Zahl In diesem Fall wäre der zusätzlich Parameter durch die Approximationszahl a (a <= 2Bitlaenge ∧ a > 0 ) bestimmt.
Approximation einer Funktion In diesem Fall wären die zusätzlichen Parameter
der Funktionsgrad der 2-dimensionalen xa -Funktion (a <= Polynomgrad ∧ a
> 0) und der Approximationswertebereich der x-Achse.
Steuerungsaufgaben eines Kfzs Keine zusätzlichen Parameter
16
Hierbei wird Groß- und Kleinschreibung nicht berücksichtigt
71
6 Server für evolutionäre Verfahren
Skript → Problemfeld
Approximationszahl
Funktionsgrad Intervallgrenze1 Intervallgrenze2
Problemfeld → ’problem’
( ’number’ | ’function’ | ’car’ | ’vehicle’ ) ’;’
Approximationszahl → Ganzzahl ’;’
Funktionsgrad → ’x’ ’∧’ Ganzzahl ’;’
Intervallgrenze1 → Doublezahl ’;’
Intervallgrenze2 → Doublezahl ’;’
Ganzzahl → Ziffernfolge
Doublezahl → Ziffernfolge ’.’ Ziffernfolge
Ziffernfolge → Ziffer Ziffer
Ziffer → ’0’ | ’1’ | ’2’ | ... | ’9’
Abbildung 6.15.: Definition der Skriptsprache
6.5. Server-Architektur-Kommunikation
Nachdem alle Pakete des Servers für evolutionäre Verfahren besprochen worden sind,
soll im Folgenden die Kommunikation, das Zusammenspiel der einzelnen Bibliotheken anhand dreier ausgewählter Beispiele näher erläutert werden. Diese spiegeln
auch während des Entwicklungsprozesses zentrale Punkte wieder.
6.5.1. Nachrichtenorientierte Informationsverarbeitung
Ereignisgetriebene Programme enthalten eine Ereignis- oder Nachrichtenschleife,
welche aus einem blockierenden Nachrichtenempfang und einem Verteiler (Dispatcher) besteht, der Nachrichten an passende Behandler (Handler) zur Verarbeitung
verteilt.
Wie in Kapitel 6.2.2 beschrieben besitzt die EALib-Bibliothek eine Nachrichtenwarteschlange. In dieser werden Nachrichten vom Typ EAMessage für eine weitere
Verarbeitung gepuffert. Sie stellen übergeordneten Layern aktuelle Informationen
über den evolutionären Lauf zur Verfügung. Dieser befindet sich in der EAServerBibliothek und enthält die Ereignisschleife. Sie arbeitet die Warteschlange ab und
72
6.5 Server-Architektur-Kommunikation
leitet die empfangene Nachricht an die Benutzerschnittstelle EAServerUI weiter.
Dieser Mechanismus ist nochmals in der EAServer-Bibliothek implementiert. Das
Kommunikationsmodul des Servers enthält ebenfalls eine Nachrichtenwarteschlange, in der Nachrichten des Typs EAConnectionMessage eingetragen werden können.
Diese geben Aufschluss über den Status der Verbindung. Eine zweite Nachrichtenschleife nimmt diese entgegen und vermittelt sie wieder an die GUI weiter.
Dort befindet sich der oben beschriebene Dispatcher, welcher die Ereignisobjekte
an die für sie registrierten Behandler verteilt (vgl. Tabelle 6.1). Im Fall des Event
Objects EAMessage existieren ein Handler für die Verarbeitung von Fehlerereignissen innerhalb der EALib-Bibliothek. Des Weiteren gibt es Behandler für Statistik-,
Generationen und Ende-Nachrichten. Sie geben Aufschluss über statistische Informationen des evolutionären Laufs, sowie über den Fortschritt als auch die Beendigung
dessen. Die Klasse EAConnectionMessage repräsentiert das zweite Ereignisobjekt,
welches wieder an entsprechende Handler weitergereicht wird. Es existieren Handler
für Fehler und den Verbindungsstatus (Verbunden, Nicht Verbunden).
Vorteil dieses nachrichtenorientierten Mechanismus ist es, das untergeordnete Schichten keinerlei Kenntnisse von übergeordneten besitzen müssen. Jegliche Informationen werden in eine Warteschlange eingetragen, aus der eine Anwendung diese herausnehmen und weiterverarbeiten kann. Dies garantiert jedoch keine feste Ausführungsreihenfolge von Aktionen. Im Fall der evolutionären Servers ist es aber nicht
notwendig, da es sich hier lediglich um Statusinformationen über den evolutionären
Lauf bzw. des Verbindungsstatus handelt. Die Verarbeitungsweise dieser Informationen ist somit der Benutzerschnittstelle freigestellt.
Abbildung A.4 zeigt nochmals die hier beschriebenen Zusammenhänge im Bild.
6.5.2. Kommunikationsauf- bzw. -abbau
Für die Optimierung mancher Problemfelder, wie zum Beispiel der Steuerungsaufgaben eines Fahrzeugs, ist die Herstellung einer Verbindung zu einem Klienten für
den evolutionären Lauf unabdingbar. Das problemabhängige Bewertungsmodul bedarf hier für die Berechnung der Qualität der Individuen eines externen Programms
(Fahrzeugsimulation). Im Folgenden wird der implementierte Mechanismus zur Herstellung einer Verbindung näher erläutert. Abbildung A.5 zeigt diesen nochmals als
UML Sequenzdiagramm.
Die Benutzerschnittstelle startet den Kommunikationsaufbau, indem ein neuer Ar-
73
6 Server für evolutionäre Verfahren
Ereignisobjekt
Handler
Beschreibung
Error
Verarbeitung der Fehlerinformationen der mit dem
evolutionären Lauf in Verbindung
stehenden Komponenten
Verarbeitung der Statistik
des evolutionären Laufs: beste,
schlechteste Fitness,
Varianz der Fitness usw.
Verarbeitung der Information
über das Ende einer Generation
Verarbeitung der Information
über das Ende des evolutionären Laufs
Verarbeitung der Fehlerinformation
des Kommunikationsmoduls
Verarbeitung der Information
über den Verbindungsstatus:
verbunden
Verarbeitung der Information
über den Verbindungsstatus:
nicht verbunden
Statistic
EAMessage
Generation
Finish
Error
Connected
EAConnectionMessage
Disconnected
Tabelle 6.1.: Ereignisobjekte und Handler des evolutionären Servers
beitsthread EAConnectionThread angelegt und ausgeführt wird. Dieser führt die native Funktion zum Öffnen einer Verbindung aus (eaOpen). Diese Nebenläufigkeit ist
notwendig, da sonst die Benutzeroberfläche für die Dauer des Verbindungsaufbaus
blockiert wäre (vgl. Kapitel 6.4.1). Nun wird die für die gewünschte Verbindungsart
nötige Klasse instanziiert (EATCPSocket), was eine Instanziierung der Idle-ThreadKlasse (EAIdleConnectionThread ) und der Socket-Klasse (Socket) zur Folge hat.
Es wird eine Verbindung geöffnet, indem ein blockierender Funktionsaufruf (listen)
getätigt wird. Dieser horcht solange auf einen gewünschten Port, bis ein Verbindungswunsch eines Klienten eintrifft und die Verbildung akzeptiert wird. Danach
wird die Kommunikation in den Idle-Modus versetzt (setIdle(true)), was bedingt
dass ein Idle-Thread gestartet wird, welcher selbst die blockierende Funktion re-
74
6.5 Server-Architektur-Kommunikation
ceive aufruft. Parallel hierzu wird die Nachrichtenverarbeitung gestartet. Jegliche
Information bzgl. dieser Kommunikation werden hierüber an die GUI weitergeleitet,
welche das Dispatching durchführt. Eine genaue Erläuterung dieses Mechanismus
wurde im Kapitel 6.5.1 gegeben. Wünscht die Benutzeroberfläche die Verbindung
zu schließen, so wird die native Funktion eaClose aufgerufen, welche bewirkt, dass
der Server entsprechend dem Kommunikationsprotokoll dem Klienten eine BYENachricht sendet, so dass jener wiederum diese mit einem weiteren BYE bestätigt.
Wird ein BYE empfangen, wird die Blockade des receive gelöst und der Idle-Thread
kann sich beenden. Wünscht ein Klient die Verbindung zu beenden, so ist der Mechanismus entsprechend. Der gewünschte Kommunikationsabbau wird durch eine
BYE-Nachricht signalisiert, welche wie oben beschrieben den Idle-Thread beendet
und die Verbindung schließt. Über den Status der Kommunikation werden Nachrichten in eine Warteschlange für die übergeordnete Schichten (GUI) eingetragen.
So nach der Etablierung der Verbindung (sendMsg(”Connection”))und Terminierung
(sendMsg(”Disconnected”)) dieser. Tritt ein Fehler während der Kommunikation auf
wird ebenfalls mittels dieses Mechanismus übergeordnete Schichten informiert.
Wie bereits erläutert wurde, ist eine für die im Fall der Diplomarbeit verwendete
Kommunikation notwendige Socket-Bibliothek geschrieben worden. Nachteil dieser
Eigenentwicklung war, dass nachdem eine Verbindung hergestellt wurde, der Server
keinerlei Überwachungsmechanismus bzgl. des Status der Verbindung besaß. Beendete sich z.B. ein Klient, blieb der Server uninformiert. Aus diesem Grund wurde
der oben beschriebene Idle-Thread eingeführt, welcher ein blockierendes Receive
ausführt und somit die Verbindung beobachtet. Dieser Mechanismus macht es notwendig den Kommunikationskanal vor dem Senden von Daten aus dem Idle-Zustand
zu holen und nach dessen Verwendung in den Idle-Zustand wieder zu versetzen (vgl.
Kapitel 6.3.5). Während einer Verwendung muss selbst bzgl. Fehler geprüft werden. Die Zustandsänderung des Kommunikationskanals geht immer mit der Beendigung bzw. dem Start des zugehörigen Threads einher. Da dies nicht unmittelbar geschieht und eine Überlagerung mit einem nachfolgenden send -Befehl vermieden werden soll, mussten Sleep-Befehle über 50 Millisekunden eingeführt werden. Ebenfalls
war im Verlauf der Diplomarbeit festzustellen, dass unter Verwendung der Win32API Nachrichtenpufferung durch die API selbstständig vorgenommen wurden, und
somit die Nachrichten nicht wie implementiert sequentiell übertragen wurden. Aus
diesem Grund müssen bei den Klienten Mechanismen eingeführt werden, um solchen
Pufferungen entgegenzuwirken. Der plattformunabhängige Vorteil wirkt aber diesen
75
6 Server für evolutionäre Verfahren
Effekten entgegen.
6.5.3. Start und Terminierung des evolutionären Laufs
Für den Start des evolutionären Laufs wurde ebenfalls der in Kapitel 6.5.2 erläuterte Mechanismus verwendet. Wünscht die Applikation den Start, so wird ein GUIThread für die Nicht-Blockade der Darstellung ausgeführt, welcher die native Funktion eaExecute aufruft. Diese bewirkt innerhalb der EAServer-Bibliothek, dass eine Instanz der Klasse EvolutionAlgorithm der EALib-Bibliothek gebildet wird. Für
die nachrichtenorientierten Informationsverarbeitung ist Nebenläufigkeit notwendig.
Aus diesem Grund erhält der evolutionäre Lauf seinen eigenen Arbeitsthread. Die
Nachrichtenschleife leitet alle Nachrichten zum Dispatching an die GUI weiter. Wird
eine Ende- bzw. Fehler-Nachricht erhalten, so beendet sich zusätzlich der Thread.
Wünscht die Applikation die Beendigung des evolutionären Laufs, so wird dies dem
Steuermodul über die native Funktion eaTerminate und dem Wrappermodul der
EALib-Bibliothek mitgeteilt. Dies hat wieder die Beendigung des Threads zur Folge.
Abbildung A.6 zeigt diese Zusammenhänge nochmals als UML Sequenzdiagram.
6.6. Zusammenfassung
Aufgrund der an die Diplomarbeit gestellte Anforderung der Plattformunabhängigkeit, wurde
die Benutzeroberfläche des Servers für evolutionäre Verfahren mittels der Programmiersprache
Java und unter zur Hilfenahme des Swing- Frameworks programmiert. Da jedoch die Bibliotheken aus Effizienzgründen in der kompilierten Sprache C++ erstellt worden sind, resultierte dies in der Implementierung eines Wrappers, welcher die Aufgabe übernimmt, die eingesetzten Technologien zu vereinen. Die EALibBibliothek bildet hierbei die unterste Schicht der
Abbildung 6.16.: Server-Pakete
Server-Software. Sie übernimmt die Funktionalität der problemunabhängigen Aufgaben eines genetischen Algorithmus. Jegliche
76
6.6 Zusammenfassung
problemabhängige Funktionalität wurde durch die EAServer-Bibliothek gekapselt,
welche neben der erwähnten Vereinigung der Hochsprachen C++ und Java ebenfalls Server-Funktionalität für die Anbindung von Clients zur Verfügung stellt. Die
Pakete EALib, wie auch EAServer wurden unter dem Gesichtspunkt der Erweiterbarkeit programmiert. Wie in den jeweiligen Kapiteln erläutert wurde, sind diverse
Software-Patterns eingesetzt worden, um dies zu erreichen. So ist es nicht nur möglich die in Kapitel 3 beschriebenen Strategien eines genetischen Algorithmus einzubinden, sondern auch zusätzlich zu diesen weitere. Die explizite Trennung zwischen
problemabhängigen und problemunabhängigen Teilen eines genetischen Algorithmus, welche sich ebenfalls im Softwaredesign niedergeschlagen hat, erlaubt es für
diverse konkrete Probleme passgenaue genetische Operatoren zu schreiben, so dass
die Effizienz des Algorithmus gesteigert werden kann. Darüber hinaus können neben
Mutation und Crossing-over Strategien auch weitere fortgeschrittenere Operatoren
(vgl. Kapitel 3.4.5) implementiert und in den Algorithmus eingebracht werden. Diese
Erweiterbarkeit lässt es zu, das Paket EALib nicht nur für definierte Projekte einzusetzen, sondern für jede denkbar zu optimierenden bzw. lösenden Problemfelder.
Durch das Kommunikationsmodul innerhalb des EAServer-Pakets wurde die Möglichkeit geschaffen Klienten für diverse Aufgaben an den Algorithmus zu binden; sei
es für reine Visualisierung oder aber auch für die Einbindung in die Bewertung der
Individuen. Da es auch durch die Konzeption als verteiltes System denkbar ist, dass
Klienten nicht nur Applikationen sondern auch mobile Roboter oder anderweitige
Anwendungen seien können, ermöglicht dieses Kommunikationsmodul durch seinen
modularen Aufbau die Eingliederung bzw. Erweiterung verschiedener Kommunikationstechnologien: LAN, IrDA, Bluetooth, WLAN, usw.
Durch die Benutzeroberfläche selbst wurde eine Anwendung geschaffen, welche es
ermöglicht, einen genetischen Algorithmus in seiner Gesamtheit zu konfigurieren,
auszuführen und über den Lauf hinweg statistische Daten zu sammeln, mittels dieser Auswertungen getätigt und Aussagen über die Effizienz getroffen werden können.
Der Server für evolutionäre Algorithmus versteht sich als Test-Framework für zu optimierende bzw. lösende Problemfelder. Er beschränkt sich dabei nicht auf die in
dieser Diplomarbeit durchgeführten Versuche, sondern soll aufgrund seines Designs
einer stetigen Entwicklung unterliegen und zukünftigen Projekten als Basis dienen.
77
7. Fahrzeugsimulation
7.1. Konzept
7.1.1. Ziel
Zum Zwecke der Erprobung verschiedener genetischer und evolutionärer Verfahren
sollte eine Simulation entwickelt werden, die das Verhalten eines Fahrzeugs bei niedrigen Geschwindigkeiten abbildet.
Diese Simulation sollte eine Welt in der Größenordnung einiger Straßenzüge darstellen, in der sich das Fahrzeug weitestgehend frei bewegen kann.
Um komplexere Manöver erarbeiten zu können, sollte zusätzlich zum Fahrzeug auch
das Verhalten eines gezogenen Anhängers umgesetzt werden.
Die simulierte Welt enthält nicht nur frei befahrbare Bereiche, sondern auch Hindernisse, wie Mauern und parkende Fahrzeuge, die es ermöglichen, verschiedene
Szenarien für das Lernen komplexer Manöver zu gestalten. Neben der rechnenden
Simulation wird eine Darstellung benötigt, die es dem Benutzer ermöglicht, die Bewegung des Fahrzeugs zu verfolgen. Diese Darstellung soll in 3D erfolgen, um dem
Benutzer eine realistische Vorstellung einer denkbaren praktischen Anwendung zu
vermitteln.
7.1.2. Überlegungen zur Simulation
Simulation ist eine Vorgehensweise überwiegend zur Analyse dynamischer Systeme.
Bei der Simulation werden Experimente an einem Modell durchgeführt, um Erkenntnisse über das reale System zu gewinnen. Im Zusammenhang mit Simulation spricht
man von dem zu simulierenden System und von einem Simulator als Implementation oder Realisation eines Simulationsmodells. Letzteres stellt eine Abstraktion des
zu simulierenden Systems in Bezug auf Struktur, Funktion und Verhalten dar. Der
79
7 Fahrzeugsimulation
Ablauf des Simulators mit konkreten Werten wird als Simulationsexperiment bezeichnet. Dessen Ergebnisse können dann interpretiert und auf das zu simulierende
System übertragen werden.
Ein Auto-Crashtest beispielsweise ist ein Simulationsmodell für eine reale Verkehrssituation, in der ein Auto in einen Verkehrsunfall verwickelt ist. Dabei wird die
Vorgeschichte des Unfalls, die Verkehrssituation und die genaue Beschaffenheit des
Unfallgegners stark vereinfacht. Auch werden keine Personen in den simulierten Unfall involviert, sondern es werden stattdessen Crashtest-Dummies eingesetzt, die mit
realen Menschen gewisse mechanische Eigenschaften gemeinsam haben. Ein Simulationsmodell hat also nur ganz bestimmte, ausgewählte Aspekte mit einem realen
Unfall gemeinsam. Welche Aspekte dies sind, hängt in erster Linie von der Fragestellung ab, die mittels Simulation beantwortet werden soll.
Simulationen werden vor allem dann eingesetzt, wenn die Untersuchung am realen
System zu aufwändig, zu teuer oder zu gefährlich wäre. Typischerweise werden sie
auch zur Entwickelung eines neuen Systems verwendet. In diesem Zusammenhang
ist der Windkanal zur Verbesserung der aerodynamischen Eigenschaften z.B. eines
neu designeten Flugzeugs ein bekanntes Beispiel.
Gerade in den letzten Jahren haben die computergestützten Simulationen einen immer größer werdenden Anteil an der Planung und Erprobung neuer oder verbesserter
Systeme. Sie ermöglichen uns Vorhersagen, die vorher unvorstellbar waren, mit einer
Präzision, die ständig besser wird.
Der größte Nachteil einer Simulation ist die notwendige Vereinfachung der Naturgegebenheiten. Dies ist erforderlich, um das Modell im Computer in vertretbarer Zeit
berechnen zu können. Auch kann nicht immer gewährleistet werden, dass alle notwendigen Parameter erfasst und in die Simulation übertragen wurden. Selbst wenn
das gelingen sollte, bleibt immer noch die Ungenauigkeit der Rechner, die, trotz
wachsender Präzision, Rundungsfehler nicht ausschließen können.
Im Falle der hier entwickelten Simulation wurde der Präzisionsverlust durch die Vereinfachung der Fahrphysik einerseits gegen den erhöhten Rechenaufwand einer komplexen Physiksimulation andererseits abgewogen. Da gerade in der Entwicklungsund Erprobungsphase die höhere Geschwindigkeit eines vereinfachten Modells einen
entscheidenden Vorteil gegenüber einer moeglicherweise erreichbaren hoeheren Genauigkeit hat, wurde hier dem vereinfachten Modell der Vorzug gegeben.
80
7.1 Konzept
7.1.3. Arbeitsweise einer Simulation
Eine Simulation bildet ein gegebenes System auf ein Modell ab und ermöglicht es,
aus simulierten Experimenten Rückschlüsse auf das System zu ziehen.
Hierzu benötigt die Simulation zunächst eine Darstellung des Systems, die durchgerechnet werden kann. Üblicherweise werden alle selbstständig funktionierenden
Bestandteile einzeln abgebildet und beeinflussen sich später gegenseitig.
Im Falle der hier beschrieben Fahrzeugsimulation werden also das Fahrzeug, der
Anhänger, Hindernisse sowie Freiflächen unabhängig voneinander abgebildet.
Ist das Modell erzeugt, können Berechnungen daran vorgenommen werden. Hierzu
gibt es hauptsächlich zwei Standardverfahren, die je nach Anwendungszweck mehr
oder weniger sinnvoll sind.
Zeitgesteuerte Simulationen berechnen die geschätzte Situation aus einer Ausgangssituation und einer gegebenen Zeitspanne. Oftmals muss zur Bestimmung der
neuen Situation die Wechselwirkung der einzelnen Bestandteile mehrmals durchgerechnet werden. Dieses Verfahren ermöglicht es z.B., einzelne Zeitpunkte gezielt
herauszugreifen und zu betrachten. Die Präzision lässt sich nicht durch Veränderung
der Zeit, sondern nur durch die Zahl der berechneten Wechselwirkungen erhöhen.
Es ist somit möglich, mit der selben Simulation grobe, schnell zu berechnende Vorgaenge, genauso wie Feine zu berechnen, die mehr Rechenaufwand mit sich bringen.
Dieses System wird z.B. bei Wettervorhersagen genutzt.
Schleifengesteuerten Simulationen verzichtet auf die Zeit als variablen Parameter. Sie berechnet die neue Situation durch ständiges Anwenden der selben Operationen. In jedem Schleifendurchlauf werden also alle Wechselwirkungen berechnet.
Auf diese Art steuert die Geschwindigkeit der Berechnungen die vergehende Zeit.
Die Präzision lässt sich hier durch Reduktion der angewandten Änderungen erhöhen.
Dieses Verfahren findet beispielsweise bei Computer-gestützten Crashtests Anwendung.
Für das hier behandelte Problem wird das Modell der schleifengesteuerten Simulation anwendung finden.
81
7 Fahrzeugsimulation
7.1.4. Manövrierendes Fahrzeug als Modell und System
Betrachtet man die Bewegungen eines Fahrzeugs unter Einfluß der physikalischen
Gesetze, so lässt sich erkennen, dass diese unter anderem von folgenden Größen
abhängt:
• Beschleunigung
• Reibung
• Trägheit
• Fliehkräfte
Alle diese Einflussgrößen müssten berücksichtigt werden, wenn die Steuerung eines
Fahrzeugs exakt abgebildet werden soll. Da das Fahrzeug sich im Rahmen dieser Simulation stets nur mit einer zum Einparken geeigneten Geschwindigkeit fortbewegt,
können viele dieser Einflüsse vernachlässigt werden.
Die Fahrzeugbewegung lässt sich daher auf ein mathematisches Modell abbilden.
Dieses basiert auf der Verschiebung der Fahrzeugposition um einen der Geschwindigkeit entsprechenden Vektor. Dies geschieht in regelmäßigen Zeitabständen, die
durch die Simulationsschleife gesteuert werden.
Auch in der Verwendung dieses Modells zeigt sich eine weitere Ungenauigkeit. Da der
Bewegungs-Vektor eine bestimmte Größe haben muss, ist die Bewegung des Fahrzeugs stets als stufenweise anzunehmen. Es ist möglich, bei Bedarf die Präzision zu
erhöhen, indem die Länge des Vektors verkürzt wird, die Zeit-Intervalle also verkürzt
werden. Dies ist nur dann notwendig, wenn entscheidende Ereignisse zwischen zwei
Zeitpunkten eintreten, der exakte Zeitpunkt oder die exakte Position aber benötigt
wird.
Für die hier entwickelte Simulation reicht die Präzision, die durch Schleifensteuerung erreicht werden kann, aus.
Ein ähnliches Vereinfachungsmodell wird auch für den Anhänger Anwendung finden.
Auch hierzu wurde das System aus Zugmaschine und Anhänger analysiert und auf
ein einfaches mathematisches Modell abgebildet.
Dieses basiert wie das des Fahrzeugs auf Vektor-Rotation und Punktverschiebung.
Näheres zu diesem Thema findet sich im Kapitel 7.2.2 „Physik des Fahrzeugs“.
82
7.2 Umsetzung
7.1.5. Abbildung der Welt
Neben der Physik des Fahrzeugs und des Anhängers müssen auch die einfacheren
Objekte der simulierten Welt bedacht werden. Für die entwickelte Simulation sind
dies die durch Mauern oder andere Fahrzeuge blockierten Bereiche der Welt.
Um die Konstruktion der Welt zu vereinfachen, wurde diese auf ein Kästchenmodell
abgebildet. Über die gesamte Fläche der Karte wurde ein Raster gelegt, das nur
blockierte oder passierbare Felder kennt. Dieses Modell erleichtert die Erzeugung und
Speicherung sowie die Übertragung und Rekonstruktion der simulierten Umgebung.
7.2. Umsetzung
7.2.1. Entwicklungs-Umgebung
C#- Programme werden in der .NET- Laufzeitumgebung ausgeführt. Das .NETFramework stellt hierzu viele Funktionen zur Verfügung. Dies bedeutet allerdings,
dass viele Vorgänge im Gegensatz zu C++ nicht mehr der Steuerung des Programmierers unterliegen. Quellen werden in Assemblierungen kompiliert, die sowohl den
kompilierten Code (ausgedrückt in der .NET- Zwischensprache IL) als auch Metadaten zur Beschreibung des kompilierten Codes enthalten. Der IL-Code (Intermediate
Language) wird dann in der CLR (Common Language Runtime) ausgeführt. Nachfolgend werden einige weitere Unterschiede zu C++ bzw. Java genannt:
Im Gegensatz zu C++ werden bei C# keine Header - Dateien verwendet. Um eine
schnellere Analyse des C#- Codes zu erzielen, werden keine Makros unterstützt.
Auch auf Vorwärtsdeklarationen wurde verzichtet, da die Reihenfolge der Klassen
in den Quelldateien nicht von Bedeutung ist. Das Löschen von Objekten erfolgt
in C#-Programmen über die Speicherbereinigung und wird ausgeführt, wenn das
Objekt nicht länger benötigt wird. Destruktoren (=Finalisierungs-routinen) können
zur Durchführung von Bereinigungsaufgaben eingesetzt werden, dies jedoch nicht
im gleichen Umfang wie bei C++- Destruktoren.
Ein wesentlicher Nachteil von C# ist, dass die entwickelten Programme nur auf den
Microsoft-Plattformen ablauffähig sind.
83
7 Fahrzeugsimulation
7.2.2. Physik des Fahrzeugs
Die Simulation berechnet die Bewegung des Fahrzeugs aus der Position und der
Verdrehung, den sogenannten Ausgangsparametern, sowie der Geschwindigkeit und
des Lenkeinschlages. Wie bereits oben erläutert wird ein diskretes Simulationsmodell Anwendung finden, welches die neue Situation aus den Ausgangsparametern
unter Anwendung einer Zeitspanne berechnet. Diese Zeitspanne ist immer gleich,
unabhängig davon, wie lange ein Schleifendurchlauf dauert. Diese Zeitspanne wird
im folgenden als Tick bezeichnet. Mit jedem Tick wird das Fahrzeug um den Wert
der Geschwindigkeit verschoben. Befindet sich das Fahrzeug also auf dem Punkt
0,0 mit der Ausrichtung 0, was der positiven x-Richtung entspricht, und hat es die
Geschwindigkeit 4, befindet es sich nach einem Tick auf dem Punkt 4,0 nach zwei
Ticks auf 8,0 usw.
Abbildung 7.1.: Geradeausfahrt
Es wird hier unterstellt, dass die angewandte Präzision ausreichend ist, um keine
kritischen Falschberechnungen zu erhalten. Kommt ein Lenkeinschlag hinzu, wird
das Fahrzeug zunächst gedreht und anschließend verschoben. Die neue Rotation des
Fahrzeugs ergibt sich durch Addition der Bisherigen und des Lenkeinschlages.
Der Verschiebungsvektor wird nach folgender Formel berechnet, wobei Rotation die
neu ermittelte Verdrehung des Fahrzeugs ist.
dx = Cos(Rotation*PI/180)*speed
dy = -Sin(Rotation*PI/180)*speed
Der Positionspunkt des Fahrzeugs wird um den Vektor (dx,dy) verschoben.
84
7.2 Umsetzung
Abbildung 7.2.: Kurve mit Drehung um den Mittelpunkt
Das Fahrzeug wird hier um den Mittelpunkt des repräsentativen Rechtecks gedreht.
Dies erscheint dem Betrachter nicht realistisch. Um wirklich glaubhafte Bewegungen
zu erzielen wird der Drehpunkt des Fahrzeugs auf dessen Hinterachse verschoben.
Abbildung 7.3.: Kurve mit Drehung auf der Hinterachse
Die hier gewählte Physik liefert ausreichend gute Ergebnisse, welche die Bewegung
des Fahrzeugs glaubhaft abbilden. Möchte man die Realitätsnähe des Modells erhöhen könnte man hier am besten Ansätzen und die gewählte Physik durch eine
komplexere ersetzen.
Die verwendete Geschwindigkeit ergab sich aus Tests zum Wegfinde-Algorithmus.
Wird sie zu groß angesetzt wird es schwieriger, die Spur zu halten, die für das Fahrzeug berechnet wurde. Es wurde befürchtet, dass dieses Verhalten Einfluss auf das
Lernen des Einparkens haben könnte. Dies kann zwar nicht ausgeschlossen werden,
es kann jedoch gesagt werden, dass der evolutionäre Algorithmus auch bei verschiedenen Geschwindigkeiten Lösungen finden kann.
85
7 Fahrzeugsimulation
7.2.3. Physik des Anhängers
Um die Bewegungen des Anhängers realistisch abzubilden, wurde überlegt, was den
Anhänger in seine Spur bringt.
Der Anhänger wird vom Fahrzeug gezogen bzw. geschoben. Er folgt also immer dessen Bewegungen. Für die Simulation bedeutet dies, dass der Abstand zwischen der
Anhängerkupplung und dem Drehpunkt des Anhängers konstant ist. Bei seinem Bestreben dem Fahrzeug zu folgen, nimmt der Anhänger immer den kürzest möglichen
Weg.
Um dies umzusetzen, wird nach der Bewegung des Fahrzeugs ein Vektor von der
derzeitigen Position des Anhängers zur Anhängerkupplung des Fahrzeugs berechnet. Der Anhänger wird entlang dieses Vektors ausgerichtet und bis ans Fahrzeug
herangeschoben. Siehe hierzu auch Abbildung 7.4.
Abbildung 7.4.: Fahrverhalten mit Anhänger
86
7.2 Umsetzung
Es wurde des weiteren überlegt, ob es für das Einparken erforderlich sein könnte,
einen Anschlag für den Anhänger zu implementieren, der weitere Verdrehung verhindert. Es wurde davon ausgegangen, dass das Verdrehen des Anhängers über einen
bestimmten Wert dazu führt, das der Anhänger nicht wieder in die gerade Position
gebracht werden kann. Tritt dieser Fall auf, kann der Versuch als gescheitert angesehen werden und der entsprechende Fahrer wird mit hohen Strafen belegt. Dadurch
ist anzunehmen, dass auch ohne eine Begrenzung zufriedenstellende Ergebnisse erbracht werden können.
7.2.4. Die Abbildung der Welt
Die Simulation umfasst nicht nur das zu steuernde Fahrzeug und dessen Anhänger,
sondern auch Hindernisse wie beispielsweise parkende Fahrzeuge, dargestellt durch
entweder freie oder blockierte Felder.
Die objektorientierte Programmierung bildet jedes dieser eigenständigen Objekte in
eine eigene Klasse ab. So sind Fahrzeuge z.B. Instanzen der Klasse Car während
blockierte Felder zur Klasse WallBlock gehören. Alle Objekte haben einige Eigenschaften gemein. Offensichtlich ist, dass sie alle in der selben Welt abgebildet sind.
Daher erben alle diese „Objekt Klassen“ von der WorldObject -Klasse, die für alle
Unterklassen die selben Strukturen zur Verfügung stellt. Alle Objekte, die Teil der
simulierten Welt sind, haben daher die folgenden Member-Variablen:
• Ein Rechteck, welches als Schablone für die Schaffung der repräsentativen Region fungiert. Es wird außerdem verwendet, um den Outbound circle zu berechnen.
• Die repräsentative Region. Sie stellt die vom Fahrzeug eingenommene Fläche
dar und wird für die Kollisionsabfrage verwendet.
• Outbound Circle. Verringert den Rechenaufwand bei der Feststellung einer
Kollision.
• Die Position als Punkt/Vektor. Die Position wird unter anderem bei der Berechnung der Region verwendet.
• Rotation. Gibt die Verdrehung des Objekts an.
87
7 Fahrzeugsimulation
• Eckpunkte der Region. Diese werden bei Erzeugung des Objekts, bzw. bei Veränderung berechnet. Sie sind Bestandteil der beschleunigten Kollisionsabfrage.
• Die statische Angabe der Größe eines Feldes in der Simulierten Welt. Diese
wird für verschiedene Berechnungen verwendet und ist für alle Objekte gleich.
Neben diesen allgemeinen Strukturen ist das wichtigste Element, das die WorldObject -Klasse bietet, die Funktion zur Kollisionsabfrage. Diese stellt fest, ob sich zwei
Objekte der simulierten Welt berühren oder überlappen.
Wenn das Fahrzeug auf eine Wand trifft, soll dies erkannt und bei Bedarf entsprechend behandelt werden können. Da in dieser Simulierten Welt alle Objekte wie
Rechtecke behandelt werden, lässt sich eine Kollisionsabfrage einfach implementieren.
Eine zunächst verfolgter Ansatz ist, mit Hilfe der Eckpunkte der Rechtecke zu arbeiten. Um eine Kollision zu erkennen, muss festgestellt werden, ob ein Eckpunkt
eines Objekts innerhalb der von den Eckpunkten eines anderen Objekts markierten
Fläche liegt. Hierzu wird jeweils die Verbindungsgerade zweier benachbarter Punkte
berechnet. Dann wird überprüft, ob der zu testende Punkt rechts oder links von
dieser Geraden liegt. Verbindet man die Punkte im Uhrzeigersinn und dreht das
Koordinatensystem jeweils so, dass die momentan betrachtete Gerade parallel zur
y-Achse verläuft, wobei der erste Punkt tiefer auf dieser Geraden liegt, so befinden
sich alle Punkte, die innerhalb des Rechtecks liegen, von jeder Geraden des Rechtecks aus rechts. Liegt der zu testende Punkt also links einer Geraden, so befindet er
sich außerhalb der gegebenen Objektfläche.
Dieses Verfahren kann auf Polygone beliebiger Ordnung erweitert werden und gilt
als recht effektives Überprüfungsverfahren.
Im .NET Framework gibt es sogenannte Regionen, die eigentlich zur Ausgabe von
2D-Graphik eingesetzt werden. Für diese Regionen ist eine Funktion implementiert,
welche überprüft, ob ein gegebener Punkt im Inneren der Region liegt. Da anzunehmen ist, dass die Regionen und die benötigte Überprüfung sehr effizient implementiert sind, wird letztlich entschieden, diese zur Kollisionserkennung zu verwenden.
Um dies zu ermöglichen, werden die Objekte als Regionen verwaltet. Die meisten
Objekte in der simulierten Welt sind statisch, so dass die einmalige Berechnung der
Region einen geringen Zeitaufwand erfordert. Da es eine Vielzahl von Operationen
zur Manipulation einer Region gibt, erleichtert ihre Verwendung die weitere Entwicklung der Simulation ganz erheblich.
88
7.2 Umsetzung
Zur Bestimmung einer Kollision bedarf es neben der Region auch noch ihrer Eckpunkte.
Anhand dieser Informationen kann überprüft werden, ob sich ein Eckpunkt eines
Objektes innerhalb der Region eines anderen Objektes befindet. Ist dies der Fall
handelt es sich um eine Kollision zwischen den beiden Objekten. Es müssen jeweils
alle Eckpunkte des Einen und alle Eckpunkte des anderen Objektes überprüft werden. Um eine Kollision zu erkennen, ist es hinreichend, wenn NUR EIN Punkt in der
Region des anderen Objektes liegt. Für das Gegenteil müssen dagegen alle Punkte
überprüft werden.
Um dieses Vorgehen zu beschleunigen, wird zusätzlich der Radius des Outbound
Circles gespeichert, also der Radius des Kreises, auf dem der vom Mittelpunkt aus
entfernteste Punkt der Region liegt. Damit ist sichergestellt, dass die gesamte Fläche
des Objektes innerhalb dieses Kreises liegt. Zwei Objekte können nur dann kollidieren, wenn sich ihre Kreise wenigstens berühren. Dies lässt sich überprüfen, indem
die Summe der OutboundCircle beider Objekte mit dem Abstand ihrer Mittelpunkte verglichen wird. Nur wenn diese größer ist, kann eine Kollision bestehen und nur
wenn das der Fall ist, ist eine genauere Überprüfung notwendig.
7.2.5. Umsetzung der Simulation
SimulationMainClass
Im Mittelpunkt der Simulation steht die SimulationMainClass. Diese verwaltet alle
zentral benötigten Objekte und stellt den Einstiegspunkt der Anwendung.
Beim Starten der Anwendung wird ein Objekt dieser Klasse angelegt und instanziiert. Dabei wird zunächst die zu verwendende Welt aus einer Datei geladen und
verschiedene notwendige Parameter gesetzt. Zuletzt wird der Timer für die Aktualisierung der View Clients gestartet. Auch der ListenServer für Verbindungsanfragen
der View Clients wird im Konstruktor angelegt. Zur Befehlseingabe wird noch der
CommandReader erzeugt, der Konsoleneingaben des Benutzers entgegennimmt.
Sind alle Vorbereitungen abgeschlossen, wird die Hauptschleife der Simulation gestartet. Diese führt in ständiger Wiederholung das Parsen erhaltener Befehle, sowie
das Berechnen des neuen Status durch. Eine solche Hauptschleife ist der zentrale
Kern jeder Simulation.
Im Wesentlichen beinhaltet die Hauptschleife nach der Befehlsabarbeitung die fol-
89
7 Fahrzeugsimulation
genden Schritte:
• Ausführen der AI zur Bestimmung der neuen Werte für Geschwindigkeit und
Lenkeinschlag.
• Durchführen eines Simulations-Ticks des Fahrzeugs mit den vorher neu errechneten Parametern.
• Durchführen eines Simulations-Ticks des Anhängers mit der neu berechneten
Stellung des Fahrzeugs.
• Durchführen der Kollisionsabfrage jeweils für Fahrzeug und Anhänger und,
falls notwendig, entsprechende Behandlung der Kollision.
• Mitführen des Parklücken-Scanners zur Erkennung der vordefinierten Parklücken
und gegebenenfalls Anstoßen des Park-/Lernvorgangs.
Diese Schleife wird solange ausgeführt, bis der Benutzer in der Konsole den Befehl
zum Beenden der Bearbeitung erteilt oder die Applikation schliesst. Geschieht dies,
werden die instanziierten Objekte gelöscht und bereinigende Befehle ausgeführt.
ViewClientTimer
Der ViewClientTimer ermöglicht es, die verbundenen ViewClients in regelmäßigen
Abständen auf den neuesten Stand zu bringen.
Hierzu wird ein Timer-Objekt verwendet, welches in der .NET Framework Class Library implementiert ist. Der Entwickler definiert für den Timer die als ElapsedEvent
aufzurufende Funktion. Ist der Timer einmal angelegt, arbeitet er in einem eigenständigen Thread, so dass das Auftreten des TimerElapsed Events keinen Einfluss
auf die übrige Simulation hat. Die Timerzeit wird auf 20ms gesetzt. Dies entspricht
später in der Darstellung 50 Aktualisierungen pro Sekunde, was flüssige Animationen ermöglicht. Der Timer selbst belastet die Systemressourcen nur gering und
arbeitet präziser als beispielsweise eine Abfrage im Rahmen der Hauptschleife.
Nach Ablauf der eingestellten Zeit tritt das Elapsed-Ereignis ein und die zugewiesene Funktion wird ausgeführt. Diese übergibt dem ViewServer die Informationen, die
benötigt werden, um das Fahrzeug und den Anhänger neu zu zeichnen. Es ist dabei
nicht von Bedeutung, ob die Benachrichtigung erfolgreich ist oder ob ein Übertragungsfehler aufgetreten ist. Diese Zeit-basierende Benachrichtigung ermöglicht es,
90
7.2 Umsetzung
die View Clients völlig unabhängig von der eigentlichen Simulation zu steuern und
gleichzeitig fließende Darstellung zu erhalten.
Die Benachrichtigung erfolgt unter Verwendung des ViewServers, so dass an dieser
Stelle der Simulation keine zusätzlichen Informationen über die Verbindungen erforderlich sind.
CommandReader
Der CommandReader nimmt Befehle des Benutzers auf der Konsole entgegen und
stellt diese der Befehle aufarbeitenden Parser-Komponente zur Verfügung.
Um Befehle einlesen zu können, wird der C# Befehl: Console.ReadLine() verwendet. Dieser liest den eingegebenen, mit Enter abgeschlossenen String aus und gibt
ihn zur weiteren Verwendung zurück. Da dieser Befehl blockierend ist, die Bearbeitung also stillsteht, bis eine Zeile vollständig eingegeben wurde, muss er in einem
eigenen Thread ausgeführt werden sofern die Bearbeitung des restlichen Programms
weiterlaufen soll. Durch das Starten eines neuen Threads werden Systemressourcen
verbraucht. Da der ReadLine-Befehl kein aktives Warten durchführt, sondern vom
Betriebssystem bei Bedarf geweckt wird, stellt dieser Thread allerdings keine große
Zusatzbelastung dar.
Es ist normalerweise üblich, Benutzereingaben zu puffern und gegebenenfalls mehrere Eingaben innerhalb eines Schleifendurchlaufs direkt nacheinander abzuarbeiten.
Dies erübrigt sich hier, da eine Abarbeitung im nächsten Tick garantiert werden
kann und in keinem Fall die Notwendigkeit besteht, ein Kommando längere Zeit
zu speichern. Die eigentliche Bearbeitung der eingegebenen Befehle erfolgt in der
Hauptschleife.
ViewServer
Der ViewServer ist für die Verwaltung der Verbundenen ViewClients zuständig.
Diese werden in einer Liste gespeichert und können über Zugriffsbefehle wie foreach() abgefragt werden. Die Verwendung einer verwalteten, dynamischen Liste aus
der .NET Framework Class Library erleichtert das Hinzufügen wie auch das Entfernen von ViewConnections.
In C# werden Verbindungsanfragen mit dem Befehl: Listener.AcceptSocket() an-
91
7 Fahrzeugsimulation
genommen. Dieser Befehl benötigt einen mit IP-Adresse und Port konfigurierten
Listener und gibt den Socket zurück, der für diese Verbindung erzeugt wurde. Als
IP-Adresse wird hier die „Any“ Adresse verwendet, die automatisch auf jedem eingerichteten Netzwerk Device einen Listener für den angegebenen Port erzeugt.
Da AcceptSocket() blockierend ist bis eine Verbindung angenommen wurde, muss
dieser Befehl in einem eigenen Thread untergebracht sein. Dieser wird mit Anlegen
des Objektes gestartet.
Ist eine Verbindung hergestellt, wird eine neue ViewConnection für die neue Verbindung erzeugt. Dem Konstruktor wird der generierte Socket als Parameter mitgegeben. Er wird im Folgenden von der erzeugten ViewConnection Instanz selbst
verwaltet. Wurde die ViewConnection erfolgreich angelegt, wird das Objekt an die
Liste der bestehenden Verbindungen angehängt.
Anschließend kehrt die Ausführung innerhalb des Listen Threads wieder an den
Ausgangspunkt zurück, so dass weitere Verbindungsanfragen angenommen werden
können.
Alle Befehle, die der Aktualisierung der View dienen, werden über den ViewServer
durchgeführt. Nur der ViewServer ist den berechnenden Bestandteilen der Simulation bekannt. Diese rufen die entsprechende Member-Funktion des ViewServers auf,
der den Befehl an alle ViewConnections in der Liste weitergibt.
Falls die Verarbeitung der Befehle auf Ebene der ViewConnection innerhalb eines
try Blocks einen Fehler feststellt, da möglicherweise die Verbindung getrennt wurde, wird der ViewServer durch werfen einer Ausnahme darüber informiert, damit er
diese ViewConnection aus der Liste entfernen kann.
ViewConnection
Die ViewConnection verwaltet die Verbindung zu einem ViewClient, der die simulierte Welt für den Benutzer darstellt. Diese Verbindungen können beliebig getrennt
werden, ohne Auswirkung auf die Simulation. Kern dieser Klasse ist der Receive
Thread und der Send-Befehl.
Der Receive Thread ermöglicht die Nutzung des blockierenden Receive-Befehls ohne
den Programmablauf zu unterbrechen. Er startet nach Anlegen des Objektes und
wird bei dessen Zerstörung beendet. Auch der Receive-Befehl ist nicht aktiv wartend, so dass die zusätzliche Belastung gering ausfällt.
92
7.2 Umsetzung
Die erwarteten Nachrichten beschränken sich auf die Bestätigung eines auf ClientSeite eingegangenen Befehls. Erst wenn diese Bestätigung erfolgt ist, kann ein weiterer Befehl gesendet werden.
Der Send-Befehl versucht, einen vom ViewServer formulierten String an den ViewClient zu senden. Hierzu wird zunächst überprüft, ob dies zu diesem Zeitpunkt
möglich ist. Wesentliches Kriterium ist dabei die erfolgte Bestätigung des vorhergehenden Befehls. Ist das Senden noch nicht möglich, wird der String verworfen und
der Befehl kehrt zurück. Dieses Verhalten ermöglicht es, zeitgesteuert Nachrichten
zu formulieren, unabhängig vom Zustand der View. Da das Ausbleiben eines versendeten Befehls höchstens das kurzzeitige Stehenbleiben des Fahrzeugs, gefolgt von
einem kleinen Sprung zur Folge hat, ist das Verwerfen einer Nachricht zumutbar.
Ist das Versenden aufgrund eines Verbindungsfehlers fehlgeschlagen, gibt der SendBefehl einen Fehlercode zurück. Der ViewServer kann die betroffene ViewConnection
dann aus seiner Liste entfernen.
Als zweiter wesentlicher Befehl steht SendCommand zur Verfügung. Dieser ist für
das Versenden von weiteren Befehlen zuständig. Im Gegensatz zum Send-Befehl wartet SendCommand bis das Senden möglich ist, schickt den Befehl ab und pausiert,
bis der Empfang des Kommandos bestätigt wurde. So wird gewährleistet, das diese,
meist kritischen Befehle vom ViewClient zur Kenntnis genommen wurden. Durch
dieses Verhalten wird die Ausführung eines Befehls verzögert, was zu einer Verzögerung des Simulations-schleifendurchlaufs führen kann.
AIServer
Der AIServer ist für die Berechnung des zu einem Zeitpunkt notwendigen Lenkeinschlags und der zugehörigen Geschwindigkeit zuständig. Der Lenkeinschlag wird je
nach Situation aus verschiedenen Quellen bezogen.
Im Normalfall fährt das Fahrzeug frei auf der Karte herum. In diesem Fall erhält
der AIServer den Lenkeinschlag vom Pathfinder, der neben der Wegplanung auch
die Berechnung der Steuerinformationen durchführt.
Wurde eine Parklücke erkannt und der Parkvorgang eingeleitet, kann der AIServer
entweder auf gespeicherte Informationen zurückgreifen oder aber eine Verbindung
zu einer Lernkomponente über die ClientCommandClass aufbauen. Während des
Lernvorgangs wird das Fahrzeug immer wieder auf den Ursprungsort zurückgesetzt.
93
7 Fahrzeugsimulation
Alternativ könnte der gefahrene Pfad in die Gegenrichtung abgefahren werden.
AIServer bestimmt die zu verwendende Berechnungsmethode über die Verwaltung
von Zuständen. Durch eine Erweiterung dieser Zustände können weitere spezialisierte Steuerungen hinzugefügt werden. Zu dieser Vorgehensweise führten Überlegungen
zu einer praktischen Verwendung der hier gewonnenen Informationen. So wäre es
z.B. durchaus möglich, Teil-Intelligenzen für die Bearbeitung anderer Aufgaben zu
entwickeln und diese situationsbedingt abzurufen, so dass sich eine komplexe Fahrzeugsteuerung aus verschiedenen Einzelteilen zusammenbauen ließe. Versuchsweise
wurde hier das Wendemanöver auf einer Spur hinzugefügt, das über einen Konsolenbefehl gestartet werden kann.
Vorstellbar wären auch andere Manöver wie etwa Slalom.
ClientCommandClass
Die ClientCommandClass verwaltet die Verbindung zur Lernkomponente.
Wesentliche Bestandteile dieser Klasse sind der Receive Thread, der Parse-Befehl
sowie der Send-Befehl. Der Receive Thread führt den blockierenden Receive-Befehl
des Sockets aus.
Wird eine Nachricht empfangen, führt der Thread den Parse-Befehl aus, der aus
dem empfangenen Byte-Array die relevanten Informationen herauszieht und diese
über Get-Funktionen dem AIServer zur Verfügung stellt.
Im Folgenden werden die bekannten Nachrichten und ihre Aufgabe erläutert.
WAKEUP: Der Server hat seinen Idle-Zustand verlassen und teilt dies dem Client
mit. Der Client antwortet seinerseits mit WAKEUP.
BYE: Der Server möchte die Verbindung beenden. Der Client antwortet mit BYE
und beendet die Verbindung.
Serverseitige Ausführung:
WORLD: Der Server fordert die Szenarienbeschreibung an. Der Client sendet ihm
Informationen über die Zielwerte.
START: Der Server startet die Abarbeitung eines Individuums. Der Client bereitet
sich vor und bestätigt mit ACK.
COMMAND: Anhängend sendet der Server die errechneten Informationen über
Lenkeinschlag und Geschwindigkeit. Der Client übernimmt diese Werte und be-
94
7.2 Umsetzung
stätigt mit ACK.
TICK: Der Server teilt dem Client hierdurch mit, dass er bereit ist, die neuen Parameter zu empfangen. Der Client sendet dem Server die Informationen über die
Position des Fahrzeugs zu, sobald sie zur Verfügung stehen.
RESET: Die Abarbeitung eines Individuums ist abgeschlossen. Die Simulation soll
das Fahrzeug zurücksetzen und auf weitere Befehle warten. Der Client gibt diesen
Auftrag an die AIServer Instanz weiter und bestätigt mit ACK.
Simulationsseitig:
CHROMTREE: Anhängend finden sich die Informationen, die notwendig sind, um
den Arithmetischen Baum nachzubilden, der Server-seitig das Chromosom eines Individuums ist. Der Client bestätigt mit ACK.
CHROMVECT: Anhängend ist das Array, das ein Individuum bei der Codierung
Vehicle beschreibt. Der Client bestätigt mit ACK.
FITNESS: Der Server wünscht den errechneten Fitnesswert zu erhalten. Sobald die
Simulation diesen berechnet hat, wird er dem Server zugesandt.
Die Unterscheidung zwischen Server-seitiger Berechnung von Lenkeinschlag und Geschwindigkeit und der Client-seitigen Berechnung ist in erster Linie historisch bedingt.
Es war ursprünglich so gedacht, dass es für den Client keinen Unterschied macht,
was für eine Lernkomponente der Server ist.
Im Rahmen der Versuchsdurchführungen hat sich aber sehr schnell gezeigt, dass der
große Aufwand an Netzwerkkommunikation die Ausführung zu langsam macht.
Daher wurde letztlich eine für die beiden entwickelten Codierungen spezialisierte
Kommunikation entwickelt, die den Aufwand reduziert und die Abarbeitung deutlich beschleunigt.
95
8. ViewClient
8.1. Konzept
Die Simulation enthält alle Bestandteile, die erforderlich sind um das Verhalten eines
Fahrzeugs mit niedriger Geschwindigkeit berechnen zu können. Sie enthält Komponenten, die Steuerbefehle zur Verfügung stellen und das Lernen übernehmen. Sie
bietet selbst jedoch keine Möglichkeit, die simulierte Welt zu betrachten und die
Ergebnisse des Lernens zu beurteilen. Für diesen Zweck wird dem Benutzer eine
Anwendung zur Verfügung gestellt, welche die grafische Darstellung übernimmt.
Das Gesamtkonzept sieht vor, dass diese Anwendung wie viele andere Komponenten
auch beliebig austauschbar ist.
Daher soll sie über TCP/IP mit der Simulation verbunden werden und über ein
definiertes Protokoll Befehle und Aktualisierungen empfangen.
Um diese Austauschbarkeit zu zeigen wurden zwei Darstellungen, eine in 2D, die
andere in 3D, entwickelt.
Im Folgenden werden zunächst die Gemeinsamkeiten der beiden Views behandelt.
Im Anschluss wird die grafische Darstellung unter Verwendung von C# bzw. Direct3D - Grafikmethoden beschrieben.
8.2. Netzwerkverbindung und -protokoll
Beide ViewClients sind mit C# entwickelt, so dass die Komponenten zur Netzwerkkommunikation für beide weitestgehend identisch sind.
Nach Start der Anwendung muss diese die Verbindung zur Simulation aufbauen.
Hierzu wurde eine Netzwerkklasse entwickelt, welche die Verbindung aufbaut, verwaltet und schliesslich wieder beendet. Hierzu wird der Befehl Connect() aus dem
.Net Framework verwendet. Scheitert der Verbindungsaufbau, wird die Anwendung
97
8 ViewClient
beendet. Dies ist z.B. dann der Fall, wenn die Gegenstelle (noch) nicht gestartet ist
oder nicht bereit ist, Anfragen entgegen zu nehmen.
Zum Erzeugen einer Instanz der Netzwerkklasse wird die Zieladresse sowie der Zielport benötigt. Die Zieladresse ist, wenn die Darstellung auf dem selben Rechner wie
die Simulation läuft, 127.0.0.1, also die Loopback-Adresse. Diese ist auch als Standard eingestellt. Der Port wurde im Rahmen der Entwicklung mit „4021“ festgelegt.
Die Wahl des Ports ist dem Entwickler überlassen, sollte sich aber nicht mit anderen
Anwendungen überschneiden.
Wurde die Verbindung erfolgreich hergestellt, wird der Haupt-thread der Kommunikation gestartet. Dieser liest in einer Schleife eingehende Nachrichten vom zugewiesenen Socket und übergibt diese dem Parser zur weiteren Bearbeitung. Alle
eingegangnen Nachrichten werden mit THANKS quittiert. Dabei ist es nicht von
Bedeutung, ob der empfangene Befehl gültig ist oder z.B. nicht in dieser Darstellung implementiert wurde.
Es ist erforderlich, dass die folgenden Nachrichten verstanden und bearbeitet werden.
• UPDATE gefolgt von den Positionsparametern des Fahrzeugs. Falls ein Anhänger aktiv ist, findet sich in der gleichen Nachricht auch der String TRAILER,
auf den dann die Parameter des Anhängers folgen.
• WORLD gefolgt von den Informationen, die benötigt werden, um die simulierte
Welt darzustellen. An erster Stelle steht, wie viele Felder die Welt breit und
hoch ist. Danach folgen codierte Informationen über das jeweilige Feld.
• COMMAND: anderweitige Befehle, die erst von der Darstellung ausgewertet
werden. Mit dieser Nachricht wird z.B. der Text übertragen, der ausgegeben
wird, wenn die Simulation auf das Verbinden mit dem EAServer wartet.
• QUIT: diese Nachricht wird empfangen, wenn die Simulation die Verbindung
beenden möchte.
Wenn COMMAND empfangen wurde, wird der nach dem Token stehende Text in
den Befehlspuffer übergenommen, wo er von der Darstellung ausgelesen und verarbeitet werden kann.
QUIT findet so gut wie keine Anwendung, da die C#-Befehle sehr gut Verbindungsabbrüche erkennen können. So ist es möglich, auch auf eine unerwartete Beendigung
98
8.3 2DView
der Verbindung zu reagieren und beispielsweise die Anwendung zu schließen. Somit
kann der ViewClient beim Beenden der Simulation ebenfalls geschlossen werden.
Die Kommunikationsklasse arbeitet gleichzeitig als Datenspeicher für die Position
des Fahrzeugs, des Anhängers und der Weltkarte.
Diese Informationen werden der Darstellung über Get-Methoden zur Verfügung gestellt.
Die Darstellung sperrt solange den Empfang neuer Befehle, bis in einem Durchlauf
alle Informationen abgerufen wurden. So wird verhindert, dass sich - bedingt durch
das Multi-threading - zwei Positionen im Verlauf einer Darstellung überschneiden.
8.3. 2DView
Die Darstellungen unterscheiden sich hauptsächlich in der verwendeten Technologie.
Für den 2D-ViewClient wurden die Grafikroutinen verwendet, die Bestandteil des
.Net Framework sind. Dadurch ergeben sich einfache Abbildungen der einzelnen Objekte. Die Darstellung ist Timer-gesteuert um gleichmäßige Frame-Werte, also Bilder
pro Sekunde zu erhalten. Der Timer wird auf 20 ms konfiguriert. Der einzige Befehl,
der durch das TimerElapsed Event ausgeführt wird, ist View.Refresh(). Dieser erklärt die Darstellung für ungültig, wodurch ein Neuzeichnen angestoßen wird. Diese
Zeitsteuerung ermöglicht es auch, die Anwendung in den Hintergrund zu verschieben
und dennoch aktuelle Darstellung zu erhalten.
Der Kern der Darstellung mit C# sind Regionen. Regionen beschreiben grafische
Formen, die aus Rechtecken und Pfaden bestehen und als Clipping Area verwendet
werden können. Hier werden sie direkt zur Darstellung verwendet, indem die jeweilige Region mit einer Farbe ausgemalt wird. Regionen können aus verschiedenen
grafischen Primitiven aufgebaut werden. Für den ViewClient werden sie aus Rechtecken durch geeignete Verschiebung und Verdrehung konstruiert.
Da außer der Region keine weiteren Informationen über die Objekte vorliegen müssen, wird eine einfache Struktur zur Abbildung gewählt. Für das Fahrzeug und den
Anhänger existiert jeweils eine Region, die im Rahmen des Paint-Vorgangs aus den
neuen Informationen des Kommunikationsobjektes neu konstruiert und zur Darstellung mit Farbe gefüllt wird.
99
8 ViewClient
Die Regionen der blockierten Felder, also der Wände und der parkenden Fahrzeuge,
werden mit Erhalt der Weltinformationen angelegt und in Containern gespeichert.
Sie verändern sich im Laufe der Simulation nicht. Alle Regionen in jeweils einem
Container werden mit der selben Farbe gefüllt.
Ein definiertes Rechteck dient als Vorlage für diese Regionen. Ist die Position des
Feldes ermittelt, wird die neue Region aus dem Rechteck erzeugt und um die Position des Feldes verschoben. Durch die Speicherung der Regionen in Containern
kann unter Verwendung der foreach-Schleife jede Region abgerufen und verarbeitet
werden.
Auf die gleiche Weise werden auch die geparkten Fahrzeuge konstruiert und abgelegt.
Das bewegliche Fahrzeug wird zu Beginn jeder Paint-Phase berechnet. Aus den erhaltenen Informationen wird die Position und die Verdrehung berechnet. Auch hier
wird die Region aus einem Rechteck erzeugt, indem es zunächst gedreht und anschließend verschoben wird.
Um es zu ermöglichen, das Fenster der Darstellung beliebig in der Größe verändern
zu können, wird noch das Resize-Ereignis der View abgefangen. Tritt dieses Ereignis
ein werden alle bisher definierten Regionen gelöscht. Aus den gespeicherten Informationen werden die Regionen dann entsprechend der neuen Fenstergröße skaliert
und neu konstruiert. Die Skalierung sorgt dafür, dass die Welt genau so groß ist,
dass sie die kürzere Kante des Darstellungsbereiches voll ausfüllt.
Die Darstellung der Regionen auf dem Bildschirm erfolgt der Reihe nach über den
FillRegion()-Befehl, dem noch ein Brush und die darzustellende Region als Parameter mitgegeben werden müssen. Es ist dabei stets darauf zu achten, dass später
ausgegebene Objekte im Vordergrund gezeichnet werden. Falls sich mehrere Grafikobjekte überlappen, sollte also vorher überlegt werden, welches im Hintergrund
sein soll.
Beim Start der Applikation öffnet sich zunächst ein Fenster, welches den Benutzer
zur Eingabe der Ziel IP Adresse auffordert. Standard ist die Loopback-Adresse.
Wird eine ungültige Adresse eingegeben, beendet sich die Anwendung.
100
8.4 3DView
8.4. 3DView
Die 3DView verwendet Befehle des DirectX SDK (Software Development Kit). Es
würde den Rahmen dieser Diplomarbeit sprengen, würde hier der vollständige Ablauf
einer DirectX-Anwendung beschrieben. Deshalb im Folgenden nur die wichtigsten
Details:
Die Grundlage des 3Dview-Clients bildet eine, unter Verwendung des Visual Studio
Wizards für DirectX Applications erzeugte, „leere“ Anwendung, die alle erforderlichen Bestandteile enthält, um einfach auf die jeweiligen Anforderungen angepasst
werden zu können.
Die größten Änderungen erfährt die Datei D3DMesh.cs. In dieser Datei finden sich
die Befehle zum Erzeugen der darzustellenden Objekte sowie zum Rendern der Szene.
Jedes Objekt, das in der Szene dargestellt werden soll, benötigt ein eigenes Mesh,
also ein Drahtgittermodell. Zusätzlich werden Informationen der Oberflächeneigenschaften benötigt. Hierzu gehören Lichtreflektion oder Eigenleuchtkraft. Wichtig
sind auch die Informationen über die zu verwendende Textur, also das über das
Drahtgittermodell zu spannende Bild.
Um das Objekt in der Szene platzieren zu können, wird außerdem die Position sowie die Verdrehung benötigt. Um all diese Informationen für jedes Objekt verwalten
zu können, wurde eine Klasse entwickelt, die neben der Speicherung der genannten
Informationen auch Methoden zum Auslesen und Zeichnen eines Modells zur Verfügung stellt. Alle Objekte werden als Instanzen dieser Klasse verwaltet.
Es hat sich jedoch gezeigt, dass diese Methode nicht sehr effektiv ist. Das Laden der
Modelle für jedes Objekt dauert recht lange; außerdem entstehen große Datenmengen.
Um Rechenleistung und Speicher zu sparen, verwenden alle Objekte der gleichen
Art auch das selbe Modell. So muss dieses nur noch einmal geladen werden und
belegt auch nur noch einen Bereich im Speicher. Für jedes mögliche Objekt wurde
hierzu eine Klasse entwickelt, die das verwendete Modell als statische Membervariable verwaltet. Somit sehen alle blockierten Felder gleich aus, genau wie alle Autos
die gleiche Darstellung haben. Es wäre möglich, z.B. das selbe Modell für alle Fahrzeuge zu laden, jedes aber mit seiner eigenen Textur zu versehen. Viele solcher
Verbesserungen der Darstellung sind vorstellbar, sind aber ohne ausführliche Auseinandersetzung mit DirectX schwer umzusetzen. Zur Vereinfachung der Arbeit mit
101
8 ViewClient
DirectX stehen 3D-Engines auf Direct3D- oder OpenGL-Basis zur Verfügung. Diese
sind häufig für bestimmte Zwecke optimiert und ermöglichen das Verwalten einer
Großzahl grafischer Objekte mit geringem Aufwand oder unterstützen automatisches Level of Detail. Da aber auch solche Engines eine gewisse Einarbeitungszeit
erfordern, wurde entschieden, bei der schlichten Direct3D-Darstellung zu bleiben.
Für jedes einzelne Objekt wird zum Zeichnen eine Transformationsmatrix erzeugt,
die bei der Berechnung der Darstellung die Informationen für die Verschiebung und
Verdrehung des Modells enthält.
In der „Render“-Schleife wird für jedes Objekt der Draw() Befehl ausgeführt, welcher
das Zeichnen des Modells übernimmt.
Der 3DView wird - im Gegensatz zur 2D-View - die Adresse des Rechners, zu dem
verbunden werden soll, als Befehlszeilenparameter mitgegeben. Die Adresse wird
nicht verifiziert. Wenn die Eingabe ungültig ist, beendet sich das Programm sofort.
102
9. Pfadfinder
Der Wegfinderalgorithmus soll es dem Fahrzeug ermöglichen, gezielt von einem
Punkt der simulierten Welt zu jedem beliebigen anderen zu gelangen. Es gibt eine Reihe erprobter Verfahren, die mehr oder weniger effektiv sind.
Im Folgenden werden einige dieser Verfahren kurz vorgestellt.
9.1. Algorithmen
9.1.1. Der direkte Weg - Luftlinie
Dieses Verfahren verbindet den Start- mit dem Ziel-punkt durch eine Gerade ohne
Berücksichtigung möglicher Hindernisse. Dieses Verfahren eignet sich nur, wenn eine solche Verbindung immer ungehindert möglich ist. Im Allgemeinen also nur für
Luftwege oder Verbindungen auf freien Flächen.
9.1.2. Dijkstra
Der Dijkstra-Algorithmus, benannt nach seinem Erfinder Edsger W. Dijkstra, findet
in einem Graphen den kürzesten Weg zwischen zwei Knoten, sofern dieser existiert.
Hierzu werden die Knoten in verschiedenen Listen gespeichert. Eine Liste beinhaltet
die Menge aller noch nicht untersuchten Knoten, eine andere die Menge der fertig
untersuchten Knoten, eine Dritte schließlich die aktuellen Knoten, sortiert nach dem
Abstand zum Startpunkt. Zu Beginn enthält die Liste der aktuellen Knoten nur den
Startknoten.
Nun werden die Nachbarknoten jeweils des Knotens mit dem geringsten Abstand
zum Start in die Liste der aktuellen Knoten aufgenommen, sofern sie noch in der
Liste der nicht untersuchten Knoten stehen. Für jeden Knoten wird jeweils sein Vorgänger vermerkt, um den Weg später vom Ziel aus rückwärts bestimmen zu können.
Sind die Nachbarn eines Knotens in die Liste der Aktuellen verschoben, wird diese
103
9 Pfadfinder
neu sortiert und der Prozess wiederholt sich. Er endet, wenn die Liste der aktuellen Knoten den Zielknoten enthält. Da Dijkstra immer den kürzesten Weg findet,
steht der Zielknoten nach dem Sortieren an erster Stelle der Liste. Das Problem des
Dijkstra-Algorithmus ist, dass die verfolgten Wege sich gleichmäßig in alle Richtungen vom Startknoten aus ausdehnen. So werden auch Wege verfolgt, die vom Ziel
wegführen. Der Dijkstra wird vor allem dann eingesetzt, wenn die Position des Ziels
vorher nicht bekannt ist, oder wenn mehrere Ziele existieren, von denen nur der Weg
zum am schnellsten Erreichbaren berechnet werden soll.
Beispiel
Abbildung 9.1.: Dijkstra: Ausgangssituation
Es soll zu der in Abbildung 9.1 dargetellten Situation der kürzeste Weg vom Startpunkt(Grün) zum Ziel(Hellblau) ermittelt werden. Die weißen Felder sind hier begehbar, die schwarzen sind blockiert.
Abbildung 9.2 zeigt die erste Phase des Algorithmus. Die Nachbarfelder des Startknotens werden in die Liste der zu bearbeitenden Knoten aufgenommen(Gelb).
Von nun an wird der Algorithmus in einer Schleife durchgeführt. Es wird, wie in Abbildung 9.3 dargestellt der Knoten mit dem bisher niedrigsten Abstand vom Startknoten zum aktuell bearbeiteten Knoten(Rot).
Seine Nachbarn werden in die Liste der zu bearbeitenden Knoten aufgenommen(Gelb).
104
9.1 Algorithmen
Abbildung 9.2.: Dijkstra: Start
Abbildung 9.3.: Dijkstra: Aktuellen Knoten festlegen und Neue aufnehmen
Abbildung 9.4.: Dijkstra: Schleifendurchlauf
105
9 Pfadfinder
Dann wird der nächste Knoten ausgewählt und dessen Nachbarn aufgenommen( Abbildung 9.4 )
Dies wird solange fortgesetzt, bis das Ziel als Knoten in die Liste der Aktuellen
aufgenommen wird.
Abbildung 9.5 zeigt einige Ausschnitte der Entwicklung während der Suche.
Abbildung 9.5.: Dijkstra: Zwischenschritte der Wegfindung
Ist das Ziel erreicht, wird wie in Abbildung 9.6, der Pfad(blau) über die gespeicherten Vorgänger von hinten nach vorne bestimmt. Das Ergebnis ist garantiert ein
kürzester Pfad zwischen Start und Ziel.
106
9.1 Algorithmen
Abbildung 9.6.: Dijkstra: Weg gefunden
9.1.3. A*
A* ist ein modifizierter Dijkstra-Algorithmus und gilt als einer der effizientesten und
meistverwendeten Wegfinde-Algorithmen. Im Unterschied zum Dijkstra berechnet
der A* - ausgehend vom aktuellen Knoten - den geschätzten Abstand zum Ziel. Es
wird derjenige Knoten als nächstes untersucht, dessen Summe aus bisheriger Weglänge und geschätztem Restabstand am geringsten ist. Auf diese Weise entwickelt
sich der Weg immer zunächst auf das Ziel zu, was in den meisten Fällen deutlich
schneller ein Ergebnis liefert. Der letztlich gefundene Weg stimmt mit dem Weg
überein, den auch ein Dijkstra-Algorithmus finden würde, ist also immer der kürzeste. Im Folgenden wird die Arbeitsweise dieses Algorithmus genauer betrachtet.
Es wird eine Liste A von „aktuellen Knoten“ verwaltet. Zu jedem Knoten wird sein
Abstand vom Startknoten s auf dem kürzesten bisher gefundenen Pfad gespeichert.
Soll außer der Länge des kürzesten Pfades auch der Pfad selbst gefunden werden,
wird bei jedem Knoten in Schritt 4. auch sein Vorgänger gespeichert. Das Ergebnis
kann dann in umgekehrter Reihenfolge (von e nach s) ermittelt werden.
1. Nimm den Startknoten s in A auf
2. Für jeden Knoten aus A: Berechne die Summe aus seinem Abstand von s
und seiner Schätzfunktion und ermittle den Knoten vmin mit der geringsten
Summe
3. Wenn vmin = e dann wurde der kürzeste Weg gefunden
107
9 Pfadfinder
4. Ansonsten nimm die Nachfolger von vmin in A auf (vmin wird „aufgelöst“) und
gehe zu 2. Ist einer der Nachfolger bereits in A enthalten, nimm die Variante
mit dem geringeren Abstand von s.
Beispiel
Abbildung 9.7.: A*: Ausgangssituation
Es soll für die in Abbildung 9.7 dargestellten Situation der kürzeste Weg vom Startpunkt(Grün) zum Ziel(Hellblau) ermittelt werden. Die weißen Felder sind begehbar,
die schwarzen sind blockiert.
Abbildung 9.8.: A*: Start
Wie in Abbildung 9.8 erkennbar, werden zunächst die Nachbarfelder des Startknotens in die Liste der zu bearbeitenden Knoten aufgenommen(Gelb).
Die Zahlen entsprechen dem geschätzten Abstand zum Ziel. Dieser wird als Anzahl
108
9.1 Algorithmen
der Felder zum Ziel berechnet, wobei blockierte Felder zunächst ignoriert werden.
Es werden nur gerade Verbindungen hergenommen.
Abbildung 9.9.: A*: Aktuellen Knoten festlegen und Neue aufnehmen
Ab dieser Situation werden die Folgenden Schritte in einer Schleife wiederholt: Wie
aus Abbildung 9.9 ersichtlich wird der Knoten, dessen Summe aus Abstand vom
Start und zum Ziel am geringsten ist, zum aktuell bearbeiteten Knoten(Rot).
Seine Nachbarn werden in die Liste der zu bearbeitenden Knoten aufgenommen(Gelb).
Ihr geschätzter Abstand zum Ziel wird berechnet.
Abbildung 9.10.: A*: Schleifendurchlauf
Der bearbeitete Knoten wird wie in Abbildung 9.10 zu erkennen in die Liste der
fertigen aufgenommen(Grau)
Ein neur aktueller Knoten wird ausgewählt und dessen Nachbarn in die Liste der zu
109
9 Pfadfinder
bearbeitenden aufgenommen.
Abbildung 9.11.: A*: Zwischenschritte der Wegfindung
Dies wird nun solange fortgesetzt, bis das Ziel als Knoten in die Liste der Aktuellen
aufgenommen wird.
Die Abbildung 9.11 zeigt einige Schritte auf dem Weg der Pfadfindung.
Ist das Ziel wie in Abbildung 9.12 erreicht, wird der Pfad(blau) über die gespeicherten Vorgänger von hinten nach vorne bestimmt. Das Ergebnis ist garantiert ein
kürzester Pfad zwischen Start und Ziel. Es ist offensichtlich, dass zum Finden dieses
Weges weniger Schritte benötigt wrden als mit dem Dijkstra Algorithmus.
110
9.1 Algorithmen
Abbildung 9.12.: A*: Weg gefunden
9.1.4. Modifikation für die Simulation
Da das Fahrzeug, bedingt durch seinen Wendekreis nicht von jedem Punkt der Weltkarte in jede Richtung fahren kann, wurden verschiedene Anpassungen erdacht, die
das Manövrieren entlang des berechneten Weges erleichtern.
• Die Wegplanung sieht vor, dass das Fahrzeug nur geradeaus bzw. schräg nach
rechts/links fahren kann. Dies ermöglicht es, das Fahrzeug ohne auf seinen
tatsächlichen Wendekreis achten zu müssen, sicher durch die Welt zu steuern.
• Schräg in eine Richtung kann das Fahrzeug nur fahren, wenn die angrenzenden
Felder nicht belegt sind. Dies stellt sicher, dass das Fahrzeug bei der Kurvenfahrt nicht an ein Hindernis stoßen kann. Alternativ müsste die Schrägfahrt
auf Beachtung der Hindernisse abgeändert werden.
• Das Fahrzeug fährt bevorzugt ohne Kurven, geradeaus fahren hat also höhere
Priorität. So wird ein realistischeres Fahrverhalten erzielt und die gewählte
Strecke ist für den Betrachter nachvollziehbar.
Beispiel
Es soll für die in Abbildung 9.13 dargestellten Situation der kürzeste Weg vom Startpunkt(Grün) zum Ziel(Hellblau) ermittelt werden. Die weißen Felder sind begehbar,
die schwarzen sind blockiert. Der Pfeil gibt jeweils die Blickrichtung des Fahrzeugs
an.
Die erreichbaren Felder werden, wie in Abbildung 9.14 dargestellt, in die Liste der
zu bearbeitenden Knoten aufgenommen(Gelb).
111
9 Pfadfinder
Abbildung 9.13.: Modifizierter A*: Situation
Abbildung 9.14.: Modifizierter A*: Start
Die Zahlen entsprechen dem geschätzten Abstand zum Ziel. Dieser wird als Anzahl
der Felder zum Ziel berechnet, wobei blockierte Felder zunächst ignoriert werden.
Diagonale Verbindungen werden als 1.5 gezählt, während gerade Verbindungen als
1 gerechnet werden.
Abbildung 9.15 zeigt, wie der Knoten, dessen Summe aus Abstand vom Start und
zum Ziel am geringsten ist, zum aktuell bearbeiteten Knoten(Rot) wird.
Die erreichberen Felder werden in die Liste der zu bearbeitenden Knoten aufgenommen(Gelb). Ihr geschätzter Abstand zum Ziel wird berechnet.
Im Folgenden wird, wie in Abbildung 9.16 dargestellt, in einer Schleife jeweils der
bearbeitete Knoten wird in die Liste der fertigen aufgenommen(Grau) und ein neuer
112
9.1 Algorithmen
Abbildung 9.15.: Modifizierter A*: Aktuellen Knoten festlegen und neue Aufnehmen
Abbildung 9.16.: Modifizierter A*: Schleifendurchlauf
aktueller Knoten wird ausgewählt und dessen Nachbarn in die Liste der zu Bearbeitenden aufgenommen.
Dies wird nun solange fortgesetzt, bis das Ziel als Knoten in die Liste der Aktuellen
aufgenommen wird.
Die Abbildung 9.17 zeigt einige Zwischenschritte des Algorithmus.
Ist das Ziel erreicht, wird der Pfad(blau), wie in Abbildung 9.18 dargestellt, über
die gespeicherten Vorgänger von hinten nach vorne bestimmt. Das Ergebnis ist garantiert ein kürzester Pfad zwischen Start und Ziel.
Diese Änderungen bedingen allerdings die Möglichkeit, ein Feld mehrfach befahren
zu können. Daher wird jedem Wegpunkt noch die Information hinzugefügt, von wo
113
9 Pfadfinder
Abbildung 9.17.: Modifizierter A*: Zwischenschritte der Wegfindung
Abbildung 9.18.: Modifizierter A*: Weg gefunden
114
9.1 Algorithmen
aus er besucht wurde und es werden Felder doppelt aufgenommen, solange ihr Ursprung verschieden ist. Auf diese Weise sind komplexe Routen möglich, ohne Gefahr
zu laufen, in Endlos-Schleifen zu geraten. Das Fahrzeug kann bereits in der Wegfindung Wendungen oder Schleifen einplanen, was das eigentliche Steuern deutlich
vereinfacht.
Abbildung 9.19.: Modifizierter A*: Komplexer Pfad
Diese Änderungen vergrößern allerdings den Suchraum bei gleicher Feldzahl, so dass
sich die Gesamtlaufzeit bis zur erfolgreichen Wegfindung verlängert.
Andererseits ermöglichen sie es, Manöver wie z.B. Ausschwenken vor einer Kurve
oder Fahren einer Schleife, um in die Ausgangsrichtung zurück zu gelangen, bereits
in die Wegplanung aufzunehmen. Somit ist der berechnete Weg mittels einfacher Befehle abzufahren, ohne dass Ausnahmen oder problematische Situationen getrennt
behandelt werden müssen.
Durch die Vergrößerung des Suchraums und der damit verbundenen Verlängerung
der Laufzeit des Algorithmus könnte die hier gewählte Lösung für sehr große Karten
unbrauchbar sein. Es wäre in diesen Fällen zu überlegen, ob es sich lohnt, Ausnahmen abzufangen und speziell zu behandeln.
Gerade für das Steuern eines Fahrzeugs durch enge Straßen liefern die gewählten
Änderungen sehr gute Ergebnisse.
115
9 Pfadfinder
9.2. Umsetzung
Der Wegfinderalgorithmus A* wurde in C++ implementiert und als Bibliothek verwendet. Der Grund für diesen Wechsel der Programmiersprache ist die Möglichkeit,
in C++ Zeiger selbst zu verwalten. Dies ist im Prinzip in C# auch möglich, führt
dort allerdings zu deutlich höherem Aufwand, während gleichzeitig die Vorteile der
verwalteten Objekte verloren gehen. Da C++ keine Verwaltung und keine spezielle
Laufzeitumgebung benötigt, erschien auch der Geschwindigkeitsvorteil überzeugend.
Der Wegfinder-Algorithmus wurde zunächst als Dijkstra entwickelt und später zu
einem A*-Algorithmus erweitert. Durch diesen Wechsel im Verlauf der Entwicklung
konnte der Geschwindigkeitsvorteil des A* deutlich beobachtet werden. Bei der Einbindung des Wegfinder-Algorithmus in die Simulation ergab sich dann der Bedarf
für die oben beschriebenen zusätzlichen Änderungen. In unserem Fall bildet sich
der Graph aus den befahrbaren Feldern der Welt als Knoten, wobei zwei Knoten
mit einer Kante verbunden sind, wenn beide Felder benachbart und befahrbar sind.
Der Algorithmus beginnt nun auf dem Startfeld und fügt alle von dort aus erreichbaren Felder der Liste der aktuellen Felder hinzu. Dies kann in C++ sehr einfach
durch Umhängen der Zeiger aus einer Liste in die andere erfolgen, was gegenüber
dem Umkopieren deutlich Rechenzeit spart. Im nächsten Schritt wird die Entfernung
von jedem dieser aktuellen Felder zum Zielpunkt ermittelt und die Liste nach diesem Wert sortiert. Das Feld mit dem geringsten Gesamtweg zum Ziel wird nun zum
neuen Ausgangspunkt des nächsten Schleifendurchlaufs. Wieder werden alle von diesem Feld aus erreichbaren Felder in die Liste aufgenommen. Allerdings wird ab jetzt
überprüft, ob das aufzunehmende Feld bereits "besucht", also überprüft worden ist.
Es wird kein Feld zweimal aufgenommen. Sind die neuen Felder bestimmt, wird
wieder der Abstand zum Ziel berechnet, die Liste sortiert und der neue Ausgangspunkt bestimmt. Dies wird solange fortgesetzt, bis der Zielpunkt erreicht ist. Der
eigentliche Pfad wird nun - wie oben geschildert - Rückwärts aus den Wegpunkten
bestimmt.
116
9.3 Vom Pfad zu den Steuerbefehlen
9.3. Vom Pfad zu den Steuerbefehlen
Die entwickelte Bibliothek berechnet nicht nur den Weg über mehrere Felder der
Weltkarte, sie bestimmt auch den einzustellenden Lenkeinschlag zu jedem Tick.
Hierzu wird angenommen, dass die Verbindung zwischen zwei benachbarten Feldern frei ist. Deshalb kann hier die Luftlinie als direkte Verbindung hergenommen
werden. Das Fahrzeug wird dazu auf den Mittelpunkt des nächsten Feldes ausgerichtet und fährt dann direkt darauf zu. Dieses Ausrichten erfolgt durch Bestimmen der
Abweichung von der geraden Ausrichtung und durch Berechnen des zur Korrektur
benötigten Lenkeinschlags. Auch bei Diagonalfahrten kann die direkte Verbindung
als frei angenommen werden, so dass auch hier die Luftlinie als Weg verwendet werden kann. In seltenen Fällen ist kein Weg zu einem anderen Feld auffindbar. Dies ist
insbesondere dann der Fall, wenn der letzte gefundene Weg das Fahrzeug direkt vor
einer Wand stehen gelassen hat. In diesem Fall wird das Fahrzeug von der Bibliothek
rückwärts gesteuert, bis ein Weg gefunden werden kann. Die Bibliothek wurde im
Rahmen der Erprobung des A*-Algorithmus so entwickelt, dass sie wiederholt ein
zufälliges Ziel auswählt, den Weg zu diesem berechnet, das Fahrzeug steuert und
bei Erreichen des Ziels den nächsten Zielpunkt wählt. Es wurde keine Schnittstelle
eingebaut, die es ermöglicht, ein Ziel von außerhalb festzulegen.
117
10. Wissenserwerb
Die Simulation soll unter anderem die simulierte, praktische Anwendung der genetischen Verfahren zeigen. Daher sollen die erarbeiteten Ergebnisse in einem Gedächtnis
gespeichert werden. Bei Wiederholung des gleichen Problems soll auf dieses bekannte Wissen zurückgegriffen werden können.
Da sich die Bedingungen von Situation zu Situation verändern, soll es möglich sein,
erworbenes Wissen auch auf andere Situationen anzuwenden.
Um Wissen effizient zu verwalten, kennt die Lerntheorie 3 verschiedene Verfahren,
die im Folgenden kurz beschrieben werden.
Überwachtes Lernen (supervised learning) nennt man das Lernen, bei dem die
Lösung des Problems einem Lehrer bekannt ist. Diese Lösung wird dem Algorithmus im laufenden Lernprozess zur Verfügung gestellt. Diese Methode wird z.B. mit
Neuronalen Netzen umgesetzt, die aus Problem-Lösungs-Paaren die Gewichtung der
Verbindungen lernen und gleichzeitig verallgemeinern. So können bei Verwendung
des Neuronalen Netzes Probleme gelöst werden, die den zuvor gelernten ähnlich sind,
zu denen aber nicht explizit eine Lösung gelernt wurde.
Unüberwachtes Lernen (unsupervised learning) bezeichnet Lernen, ohne die Lösungen im Voraus zu kennen. Der Algorithmus erzeugt für eine gegebene Menge von Eingaben ein Modell, das die Eingaben beschreibt und Vorhersagen ermöglicht. Anwendungen umfassen Clustering-Verfahren, welche Daten in mehrere
Kategorien einteilen, die sich durch charakteristische Muster voneinander unterscheiden. Ein wichtiger Algorithmus in diesem Zusammenhang ist der ExpectationMaximization(EM)-Algorithmusder interaktiv die Parameter eines Modells so festlegt, dass es die gesehenen Daten optimal erklärt. Der EM-Algorithmus legt dabei
das Vorhandensein nicht beobachtbarer Kategorien zugrunde und schätzt abwechselnd die Zugehörigkeit der Daten zu einer der Kategorien und die Parameter, welche die Kategorien ausmachen. Eine Anwendung des EM-Algorithmus findet sich
119
10 Wissenserwerb
beispielsweise in den Hidden Markov Models (HMMs). Andere Methoden des unüberwachten Lernens, z.B. Principal Component Analysis (PCA) verzichten auf die
Kategorisierung. Sie zielen darauf ab, die beobachteten Daten in eine einfachere Repräsentation zu übersetzen, die diese Daten trotz drastisch reduzierter Information
möglichst genau wiedergibt.
Bekräftigungslernen (reinforcement learning) lernt der Algorithmus durch Belohnung und Bestrafung eine policy, also eine Taktik, wie in potentiell auftretenden
Situationen zu handeln ist, um den Nutzen des Agenten (d.h. des Systems, zu dem
die Lernkomponente gehört) zu maximieren.
Das Einparken selbst wird durch genetische Verfahren gelernt. Dieses Lernen geschieht jeweils zu einem durch die Ausgangsparameter klar definierten Problem.
Damit nicht für jede Situation erneut der genetische Algorithmus verwendet werden
muss, soll das Problem in einem gewissen Rahmen verallgemeinert werden.
Für das Einparken OHNE Anhänger ist dies wesentlich einfacher als MIT, da die
Bewegung des Fahrzeugs immer gleich abläuft und das Ergebnis sich mit einer verschobenen Startposition ebenfalls nur verschiebt.
Deutlicher fallen die Veränderungen durch die Verdrehung des Fahrzeugs aus, da
sich damit die Zielposition auf einem Kreis um den Startpunkt verschiebt. Auch
hier können geringe Unterschiede allerdings ignoriert werden. Das Einparken mit
Anhänger macht deutlich größere Probleme, da bereits eine geringe Verdrehung des
Anhängers ausreicht, um die bisher erlernten Korrekturbewegungen des Fahrzeugs
unbrauchbar zu machen. Der Anhänger wird am Ziel wahrscheinlich sehr stark verdreht stehen.
Das Implementierte Lernverfahren errechnet aus der Eingabe der Ausgangsparameter einen Schlüssel, unter dem das Ergebnis abgelegt wird. Geringe Abweichungen
der Parameter werden auf den selben Schlüssel abgebildet und ermöglichen so das
Verwenden des erworbenen Wissens auch in bislang unbehandelten Situationen.
Es wurde kein Verfahren implementiert, das die erarbeiteten Lösungen verallgemeinert und so eine universell einsetzbare Lösung erzeugt.
120
Teil III.
Auswertung
121
11. Ergebnisse der evolutionären
Testprogramme
In den folgenden Kapiteln werden Anwendungen/Problemfelder von evolutionären/
genetischen Algorithmen vorgestellt, welche im Rahmen dieser Diplomarbeit untersucht wurden. Alle beschriebenen Verfahren und Algorithmen sind als C++/Java/C#Programme im Quelltext auf der beigefügten CD abgelegt.
11.1. Approximation einer natürlichen Zahl
Die einfachste Konfiguration eines genetischen Algorithmus, welche unter dem Namen Simple Genetic Algorithm (kurz: SGA) bekannt ist, wird am Beispiel der Approximation einer natürlichen Zahl näher erläutert.
Es soll eine frei wählbare natürliche Zahl im Intervall [0; ∞[ approximiert werden.
Hierbei gäbe es grundsätzlich zwei verschiedene Möglichkeiten der Codierungsform:
die Binär- bzw. Ganzzahlcodierung. Eine Ganzzahlcodierung würde hier die kompakteste Codierungsform repräsentieren. Aber aufgrund der Tatsache, dass hier ein
genetischer Algorithmus in seiner Urform näher erläutert werden soll, wurde darauf verzichtet und eine Binärcodierung verwendet. Daraus ergeben sich wiederum
zwei Möglichkeiten: die Verwendung einer Standard-Binärcodierung oder eines GrayCodes. Vor- bzw. Nachteile dieser Codierungsformen wurden bereits in Kapitel 3
besprochen.
Aufgabe des genetischen Algorithmus ist es, bei einer vorgegebenen Bitlänge n die
gewünschte natürliche Zahl zu approximieren. Jedes Individuum stellt eine binäre
Zahl der Bitlänge n dar. Zur Bewertung der Güte eines Individuums werden SollWert und Ist-Wert verglichen und der Abstand beider Zahlen im Dezimalsystem
berechnet.
F = (Sollzahl − |Sollzahl − Istzahl|)2
(11.1)
123
11 Ergebnisse der evolutionären Testprogramme
Hieraus ergibt sich ein maximaler Fitnesswert von (Sollzahl)2 , welcher die zu approximierende Zahl repräsentiert. Ebenfalls wird durch diese Bewertungsfunktion
eine Symmetrie der zu bewertenden Ist-Werte eingeführt, d.h. besitzt z.B. die zu
approximierende Zahl den Wert 15, so errechnen die Ist-Werte 5 und 25 die gleiche
Bewertungszahl (5). Alle Istzahlen größer dem Wert Sollzahl ∗ 2 erhalten definitionsgemäß die schlechteste Bewertung (1).
Dieses Maß ist ausschlaggebend für den Evolutionsprozess. Es gibt an, welche Individuen die Sollzahl gut approximieren, d.h. einen kleineren Abstand liefern und
somit mit einer höheren Wahrscheinlichkeit überleben.
Neben dieser Bewertungsfunktion gehen noch folgende weitere Algorithmus-Parameter
in die Approximation einer natürlichen Zahl ein.
• x: Zu approximierender Wert
• n: Bitlänge
• Codierungsform des x: Standard-Binärcode; Gray-Code
• Populationenmodell: Insel; Netzwerk; Seriell
• Anzahl der Populationen
• Populationengröße pro Generation
• Terminierungsart: Abbruch nach einer maximalen Anzahl an Generation; Abbruch nach Erreichen eines Konvergenzwertes; Abbruch nach Erreichen eines
Konvergenzwertes oder nach einer maximalen Anzahl an Generationen
• Crossing-over Strategie: Ein-Punkt; Zwei-Punkt; Zufallsschablone
• Crossing-over Wahrscheinlichkeit
• Mutationsstrategie: Gleichverteilt; Normalverteilt; Positionsmutation
• Mutationswahrscheinlichkeit
• Ersetzungsschema: Generational Replacement; Elitismus; Schwacher Elitismus; Delete-n-Last
• Skalierungsschema: Kein; Linear; Dynamic Power Law
124
11.1 Approximation einer natürlichen Zahl
Welche Approximationen bzw. Äquivalenzen werden für das Beispiel x = 10 gefunden? Wie erwartet findet der genetische Algorithmus für eine Codierung der Bitlänge
4 sie sehr schnell. Wie jedoch verhält es sich mit einer Codierung der Länge 20? Da
in diesem Kapitel die Simple Genetic Algorithm Variante vorgestellt wird ergeben
sich folgende Einstellungen für den Versuch die Zahl 10 zu approximieren. Da die
Parameter
Wert
x
n
Codierung
Populationenmodell
Populationenanzahl
Populationengröße
Terminierungsart
Crossing-over
Crossing-over Wahrscheinlichkeit
Mutation
Mutationswahrscheinlichkeit
Ersetzungsschema
Skalierungsschema
10
20
Gray-Code
Insel
1
100
Generation (1000) / Konvergenz (100)
Ein-Punkt
100%
Gleichverteilt
4%
Generational Replacement
Kein
Tabelle 11.1.: Algorithmus Parameter: Approximation einer natürlichen Zahl
Bewertung eines Individuums in diesem Problemfeld im Dezimalsystem errechnet
wird, ergibt sich der in Kapitel 3.2.1 besprochene Vorteil eines Gray-Codes. Zum
einen wirkt er der Nicht-Gleichwertigkeit der Positionen entgegen und zum anderen
entspricht der Übergang von n auf n+1 im Dezimalsystem ebenfalls einer Veränderung eines Bits, d.h. ist der Abstand zwischen Istzahl und Sollzahl im Dezimalsystem
1, so muss auch in der Codierung lediglich 1 Bit für das Erreichen des globalen Optimums gekippt werden.
Tabelle 11.2 nennt statistische Daten des besten erzielten evolutionären Laufs für
dieses Beispiel.
Für die Formulierung eines Ergebnisses ist zu beachten das die schnelle Konvergenz eines evolutionären Laufs gegen das globale Optimum stark abhängig von der
nach dem Zufallsprinzip initiierten Startgeneration ist. Aus diesem Grund wurden
Resultate erzielt, welche im obigen Beispiel nach 11 Generation bereits das globale
125
11 Ergebnisse der evolutionären Testprogramme
Generation
1
2
3
4
5
6
7
8
9
10
11
Max
Min
Fitness
Durchschnitt
1,0
1,0
1,0
1,0
1,0
1,0
1,0
9,0
16,0
81,0
100,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,0
1,08
1,18
3,38
29,7
Varianz
0,0
0,0
0,0
0,0
0,0
0,0
0,0
0,6336
2,3076
99,11
1130,85
Codierung
11010011110010000001
10011010001100011100
01001111010011000111
00001010001101001000
10101000001100111111
10100111110101110101
00001100001001000111
00000000000000000010
00000000000000000110
00000000000000001101
00000000000000001111
Tabelle 11.2.: Ergebnisse: Approximation einer natürlichen Zahl
Optimum, d.h. die Zahl 10 approximiert haben, jedoch auch solche, welche nach
über 400 Generationen bzw. über 1000 Generation dieses erreichten bzw. noch nicht
erreichten. Diese Situation ist in dem zu durchsuchenden Suchraum begründet; der
20-dimensionale Suchraum ist für die Approximation einer 4-Bit Zahl zu gross. Daher
lassen sich schnell bessere Ergebnisse erzielen, wenn dieser um die Hälfte reduziert
wird, oder eine komplexere Rekombinationsstrategie (Zwei-Punkt Crossing-over ) in
den Algorithmus aufgenommen wird. Ebenfalls tragen die Einführung des Elitismus
als Ersetzungsschema, wie auch das Netzwerk-Populationenmodell mit 10 Populationen zur Verbesserung der Kovergenzgeschwindigkeit des genetischen Algorithmus
gegen das globale Optimum bei. Jedoch wäre dies nicht mehr die Konfiguration eines
Simple Genetic Algorithm.
Abbildung 11.1 zeigt den Verlauf der Fitness der besten Individuen einer Generation für das obige Beispiel. Nach den ersten Geneneration waren selbst die besten
Individuen einer Generation verhältnismäßig schlecht. Erst ab Generation 8 ist eine stetige Verbesserung der Individuen festzustellen. Dies kann auf eine passende
Rekombination oder Mutation zurückgeführt werden. Sie war entscheidend für die
Konvergenz des evolutionären Laufs gegen das globale Optimum 100.
126
11.2 Automatische Formelgenerierung, genetische Prognose
Abbildung 11.1.: Fitness-Diagramm: Approximation einer natürlichen Zahl
11.2. Automatische Formelgenerierung, genetische
Prognose
Eine Anwendung von genetischen Algorithmen ist es mit ihnen mathematisch geschlossene Formeln zu finden, die beliebige Zeitreihen approximieren. Das Einsatzgebiet dieser Algorithmen umfasst u.a. Prognosen und die Approximation von Funktionen.
11.2.1. Problemstellung
Zeitreihen, Diagramme und Kurven, lassen sich selten durch geschlossene mathematische Formeln oder Gleichungen darstellen. Aktienkurse, Temperaturdaten, Absatzkurven oder chaotische Zeitreihen zeigen im Allgemeinen kaum Regelmäßigkeiten
und lassen sich daher nur schwer beschreiben und prognostizieren. Es wird versucht,
Algorithmen zu entwickeln, mit denen zuverlässige Aussagen über das Verhalten
solcher Kurven getroffen werden können. Exponentielle Glättung, ARIMA-Modelle
oder neuronale Netzwerke sind Ansätze in dieser Richtung. Im Folgenden wird einer
der Ansätze erläutert, mit dem es möglich ist, genetische Algorithmen zu verwenden,
um Zeitreihen durch mathematische Formeln beliebig genau zu approximieren und
dadurch zu prognostizieren.
127
11 Ergebnisse der evolutionären Testprogramme
11.2.2. Approximation durch Polynome
In diesem Ansatz wird versucht, Zeitreihen durch Polynome n-ten Grades zu approximieren. Als Zielfunktion, d.h. als zu approximierende Funktion wird die x3 -Funktion
gewählt:
y = fsoll (x) = x3
(11.2)
Der zu approximierenden Funktion wird ein Polynom der Form
y = fist (x) = a1 ∗ xb1 + a2 ∗ xb2 + . . . + an ∗ xbn
(11.3)
gegenübergestellt. Aufgabe des genetischen Algorithmus ist, bei einem vorgegebenen
Grad des Polynoms die Parameter ai und bi so zu bestimmen, dass die Gesamtfunktion fist (x) die gewünschte Zeitreihe möglichst gut approximiert.
Jedes Individuum stellt ein komplettes Polynom dar, das für ein bestimmtes x einen
Wert zurückliefert. Zur Bewertung der Güte eines Individuums werden m Stützstellen definiert. Diese Werte werden als Argumente in die Polynome des genetischen
Algorithmus eingesetzt und die entsprechenden y-Werte verglichen.
Für die Veranschaulichung des Verfahrens seien folgende Stützstellen angenommen:
Stützstelle
Soll-Funktionswerte
Ist-Funktionswerte
x1 = −2
x2 = −1
x3 = 0
x4 = 1
x5 = 2
fsoll (x1 ) = −8
fsoll (x2 ) = −1
fsoll (x3 ) = 0
fsoll (x4 ) = 1
fsoll (x5 ) = 8
fist (x1 )
fist (x2 )
fist (x3 )
fist (x4 )
fist (x5 )
Tabelle 11.3.: Stützstellen
Die Ordinatenwerte xi entsprechen den gewünschten Soll-Funktionswerten fsoll (xi ).
Analog hierzu werden die Ist-Werte des genetischen Algorithmus fist (xi ) ermittelt.
Ein Vergleich der Werte kann durch die Summe der absoluten Fehler über alle Stützstellen gebildet werden:
Fabs =
m
X
i=1
128
|fsoll (xi − fist (xi )|
(11.4)
11.2 Automatische Formelgenerierung, genetische Prognose
Dieses Maß bestimmt, welche Individuen im Evolutionsprozess überleben. Polynome, welche die Originalfunktion gut approximieren, d.h. die einen kleinen Fehler
liefern, überleben mit einer höheren Wahrscheinlichkeit als schlechte Polynome. Soll
der genetische Algorithmus gezielter auf das Eliminieren der schlechten Individuen
hinarbeiten, so empfiehlt sich als Bewertungsfunktion anstelle des absoluten Fehlers
der quadratische Fehler:
Fsqr =
m
X
(fsoll (xi ) − fist (xi ))2
(11.5)
i=1
Neben den Bewertungsfunktionen gehen noch folgende weitere Parameter in die
Formelgenerierung ein.
• n: Grad des Polynoms
• [xmin , xmax ]: Intervall, auf dem die Originalfunktion approximiert werden soll
• [amin , amax ]: Intervall, in dem sich die Faktoren ai des Polynoms bewegen dürfen
• [bmin , bmax ]: Intervall, in dem sich die Faktoren bi des Polynoms bewegen dürfen
• Populationenmodell: Insel; Netzwerk; Seriell
• Anzahl der Populationen
• Populationengröße pro Generation
• Terminierungsart: Abbruch nach einer maximalen Anzahl an Generation; Abbruch nach Erreichen eines Konvergenzwertes; Abbruch nach Erreichen eines
Konvergenzwertes oder nach einer maximalen Anzahl an Generationen
• Crossing-over Strategie: Ein-Punkt; Zwei-Punkt; Zufallsschablone
• Crossing-over Wahrscheinlichkeit
• Mutationsstrategie: Gleichverteilt; Normalverteilt; Positionsmutation
• Mutationswahrscheinlichkeit
• Ersetzungsschema: Generational Replacement; Elitismus; Schwacher Elitismus; Delete-n-Last
129
11 Ergebnisse der evolutionären Testprogramme
• Skalierungsschema: Kein; Linear; Dynamic Power Law
Welche Approximationen bzw. Äquivalenzen werden für das Beispiel y = x3 gefunden? Für den evolutionären Lauf werden die Parametereinstellungen von Tabelle
11.4 verwendet. Das Ergebnis dieses Laufs baut ebenfalls wie jenes aus Kapitel
Parameter
Wert
n
[xmin , xmax ]
[amin , amax ]
[bmin , bmax ]
Populationenmodell
Populationenanzahl
Populationengröße
Terminierungsart
Crossing-over
Crossing-over Wahrscheinlichkeit
Mutation
Mutationswahrscheinlichkeit
Ersetzungsschema
Skalierungsschema
10
[-2,2]
[-10,10]
[0,0]
Netzwerk
30
100
Generation (500)
Zwei-Punkt
100%
Normalverteilt
10%
Elitismus
Kein
Tabelle 11.4.: Algorithmus Parameter: Approximation einer Funktion
11.1 auf die zufallsbasierte Initialisierung der Startgeneration auf. Es wird ein 10dimensionaler Suchraum für den Algorithmus vorgegeben, in dem im Intervall [-2;2]
die x3 -Funktion approximiert wird. Die Parameter bi liegen im Intervall [0;0], d.h. sie
unterliegen nicht der Optimierung durch den Algorithmus, sondern sind feste Exponenten. Grund hierfür liegt in der Reduzierung des zu durchsuchenden Suchraums.
Nach den ersten Generationen ist das beste der (30 ∗ 100) Individuen vom genetischen Algorithmus gebildeten Polynome hinsichtlich des absoluten Fehlers noch
verhältnismäßig schlecht. Tabelle 11.5 enthält repräsentative statistische Daten des
evolutionären Laufs für das obige Beispiel.
Die Bewertung des Besten im Verlauf von 500 Generationen gebildeten Polynoms
entspricht nicht dem globalen Optimum, sondern einem Lokalen. Das Globale liegt
130
11.2 Automatische Formelgenerierung, genetische Prognose
Generation
1
7
17
30
35
38
49
102
151
218
483
500
Max
Min
0,008
1,706
3,587
4,076
8,670
11,140
24,176
33,130
47,427
49,137
143,126
143,126
4,77E-5
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
1,0E-8
Fitness
Durchschnitt
3,34E-4
0,028
0,111
0,199
0,200
0,256
0,516
1,290
1,759
2,614
2,846
5,226
Varianz
2,3E-7
0,001
0,006
0,024
0,069
0,160
0,510
1,910
5,677
5,775
11,3352
98,358
Tabelle 11.5.: Ergebnisse: Approximation einer Funktion
definitionsgeäß bei 1e300 und wird im Fall einer Bewertung von 01 als Fitness2
gesetzt. Eine Fitness von 143,126 entspricht einer Bewertung/Summenfehler von
1/143, 126 = 0, 0069868 (Codierung: 0, 999693 ∗ x3 ). Dieses Ergebnis ist für die
Approximation einer x3 -Funktion auf dem Intervall [-2;2] akzeptabel. Im Punkt 2 würde sich eine Abweichung von 0,002456 errechnen. Mit steigenden x-Werten,
würde jedoch diese Abweichung zunehmen, so ist im Punkt -100 beispielsweise eine
Abweichung von 307 gegeben. Für eine genauere Approximation wäre das Intervall
auf dem die x3 -Funktion approxmiert werden soll entsprechend zu vergrößern. Dennoch genügt dieses einer Approximation der x3 -Funktion.
Abbildung 11.2 zeigt den Evolutionsfortschritt beim Bilden des Polynoms über 500
Generationen. Die Kurve stellt dabei die Güte der besten (30 ∗ 100) Individuen der
Generationen dar.
Es ist möglich eine Funktion durch n-stellige Polynome mit reelwertigen Koeffizienten sehr genau anzunähern. Jedoch hat dieses Verfahren Schwächen bei nichtmonotonen Funktionen mit vielen Wendepunkten. Aktienkurse oder Absatzkurven
sind folglich nur schwer anzunähern. Besserung würde eine Art Fourier-Entwicklung
1
2
Funktion ist approximiert
Fitness ist die reziproke Bewertung
131
11 Ergebnisse der evolutionären Testprogramme
Abbildung 11.2.: Fitness-Diagramm: Approximation einer Funktion
mittels genetischer Algorithmen bringen. Im Gegensatz zum Polynomansatz hätte
man hier die Möglichkeit drei statt zwei Parameter zu optimieren (Amplitude, Frequenz und Phasenverschiebung).
Ein weiterer Ansatz wäre die vorangegangenen Ansätze – Appoximation durch Polynome und Fourier-Reihen – zu kombinieren und somit die Stärken der Beiden zu
nutzen. Eine weitere Verallgemeinerung der Ansätze ist eine Approximation durch
beliebige Funktionsterme. Der genetische Algorithmus bildet aus einem mathematischen Alphabet3 Formelterme und nähert sich auf diese Weise einer vorgegeben
Funktion an.
Diese Idee wird auch bei der Lösung von Steuerungsaufgaben eines Kraftfahrzeugs
zum Einsatz kommen. Die implementierte Version dieses Ansatzes ist in Kapitel
6.3.6 unter dem Paragraphen Chromosom: EAArithmeticChrom beschrieben.
Eine weitere Idee für die Optimierung von Steuerungsaufgaben eines Fahrzeugs wäre die Beschreibung der Fahrstrecke als Funktion, die Approximation dieser durch
beliebige Funktionsterme und ihrem letzlichen Abfahren durch das Fahrzeug.
Eine genauere Betrachtung der verschiedenen Möglichkeiten um die Steuerungsaufgaben eines Fahrzeugs zu optimieren bzw. zu lösen wird unter zur Hilfenahme der
in Kapitel 6.3.6 beschriebenen Codierungen im Folgenden geschehen.
3
Addition, Subtraktion, Sinus, usw.
132
12. Einparken ohne Anhänger
133
12 Einparken ohne Anhänger
12.1. Erwartung
Die im Folgende untersuchte Codierung eines Fahrers ist die Codierung Vehicle. Es
handelt sich dabei um einen Vektor von Zahlen, so dass die genetischen Operationen
optimal Anwendbar sind. Diese Codierung verwaltet die Lenkeinschläge für jeweils
einen Zeitpunkt im Format Double.
Zur Auswertung eines Chromosoms wird dieser Zahlenvektor über die NetzwerkSchnittstelle zur Simulation übertragen. Diese wählt für jeden Tick den zugehörigen
Lenkeinschlag und wendet diesen für den nächsten Tick an.
Bedingt durch die konstruierte Situation werden zum Einparken geschätzte 50 Ticks
benötigt. Dieser Wert kann je nach Position des Fahrzeugs variieren. Der Vektor hat
somit eine Länge von ungefähr 50 Werten. Die Werte jeder Stelle liegen im Bereich
von -3 bis 3, was die Mutation, die einen Wert um -1 bis +1 verändern kann, recht
kräftig ausfallen lässt. Vor der Übertragung zur Simulation werden diese Werte mit
10 multipliziert und anschließend gerundet, da die Simulation ganzzahlige Werte
zwischen -24 und +24 benötigt. Die möglichen Beträge über 24 werden als 24 interpretiert, was die Wahrscheinlichkeit eines „ganz Einschlagens“ erhöht. Mit 50 Stellen
und jeweils ca. 60 möglichen Werten ergibt dies einen Suchraum, der, je nach Situation ca. 6050 Chromosomen umfasst. Das entspricht 8 ∗ 1088 mögliche Kombinationen.
Dies sind eindeutig zu viele Möglichkeiten, um sie alle auf ihre Eignung als Lösung
zu untersuchen Auch das zufällige herausgreifen einiger Chromosomen wird keine
Lösung ergeben.
Gerade in solchen Fällen zeigen genetische Verfahren ihre Stärke.
Das rückwärts-seitwärts Einparken scheint nicht sonderlich kompliziert zu sein. Daher gibt es vermutlich eine große Vielzahl an Lösungen innerhalb des Suchraumes
und es ist zu erwarten, dass die genetischen Verfahren relativ schnell zu brauchbaren
Lösungen führen werden.
Im Folgenden soll unter anderem eine Bewertungsfunktion gefunden werden, die in
geeigneter Weise die durch ein Chromosom erbrachte Leistung anhand der Endposition des Fahrzeugs beurteilt. Ausserdem sollen verschiedene Parameter der genetischen Algorithmen auf ihre Auswirkung auf die Lösungsfindung hin untersucht
werden.
134
12.2 Von der Bewertung zur Fitness
12.2. Von der Bewertung zur Fitness
Die in der Simulation verwendeten Bewertungsfunktionen berechnen alle die Fähigkeiten des Fahrers aus dem erbrachten Ergebniss. Dabei werden die Abstände zum
Ziel hergenommen und aufbereitet. Somit ist der beste erreichbare Wert der Bewertung 0, also das erreichen des Ziels. Der EAServer funktioniert jedoch umgekehrt.
Dort ist eine grössere Fitness besser. Daher muss die Bewertung der Simulation
entsprechend umgearbeitet werden. Die beste Umrechnung währe es, die schlechtest
Mögliche Bewertung herzunehmen und von ihr die tatsächlich erreichte abzuziehen.
Die schlechteste Bewertung ist jedoch nicht bekannt und kann auch nur schwer abgeschäzt werden. Daher wurde ein anderer Ansatz verwendet. Es wird das Reziproke
der Bewertungen als Fitness verwendet. Dieser Ansatz lässt sich nur verwenden,
wenn die Bewertung 0 ausgeschlossen wird. Die errechnete Bewertung wird daher
noch um eins erhöht.
12.3. Allgemeine Versuchsbedingungen
Solange in der Beschreibung des jeweiligen Versuchs nichts anderes ausgesagt wird,
ist davon auszugehen, dass die nachfolgende Standardkonfiguration verwendet wurde:
Die Serie wird als Populationsmodell gewählt, um längere Testreihen einfach durchführen zu können.
Die Populationszahl wurde mit 100 festgelegt. Ihre Bedeutung für das Finden von
Lösungen soll später zeigen, ob dieser Wert in einem brauchbaren Rahmen gewählt
wurde.
Die Genlänge ist von der jeweiligen Situation abhängig. Gerät man an eine neue
Situation kann man erst nach einigen Durchläufen feststellen, auf welchen Wert sie
gesetzt werden sollte. Im Normalfall sind mit einer Genlänge von 50 schon optimale
Lösungen zu finden. Es kann aber auch vorkommen, dass diese nur mit einer Genlänge von 49 oder 51 möglich sind.
Der Wert Upper A gibt die Werte-Grenzen für einen Vektor an. Die Obergrenze ist
der Wert von Upper A selbst, als untere Grenze dient das negative dieses Wertes.
Die CrossOver- und Mutationsparameter werden auf den Standardwerten des EAServers belassen. Ihre Bedeutung wird später ermittelt.
Als Abbruchkriterium der Evolution wird das Erreichen der Optimallösung sowie
135
12 Einparken ohne Anhänger
Populationsmodel
Populationszahl
Problem
Genlänge
UpperA
Crossover
CO Probability
Mutation
M Probability
Termination
Generation
Convergence value
Selection
Mating
Replacement
Serie mit 20 Durchläufen
100
Vehicle
50
3
One Point
100%
Equal
4%
Convergence & Generation
Maximum 100
1000
Roulette wheel
Random
Generational
Tabelle 12.1.: Standardkonfiguration
das Überschreiten des Generations-höchstwertes gewählt. Die Optimallösung weist
einem Fahrer den Fitnesswert 1000 zu. Ob eine Beschränkung der Generationenzahl
sinnvoll ist, wird sich im Rahmen der kommenden Versuche zeigen. Es ist jedoch
anzunehmen, dass das Finden einer Lösung nach längerer, erfolgloser Suche unwahrscheinlich ist. Darauf wird später noch genauer eingegangen.
Die Selektions- und Heiratsschemen werden ebenfalls auf dem Standard des EAServers belassen.
12.4. Bewertungsfunktion
Die Bewertungsfunktion berechnet aus der Leistung eines Individuums dessen Fitness und damit seine Durchsetzungswahrscheinlichkeit innerhalb der Population. Es
gibt viele Möglichkeiten, den Wert eines Individuums zu ermitteln.
In diesen Testläufen wird ausschließlich die Endposition des Fahrzeugs nach Ablauf
der Zeit bewertet. Die zwischenzeitliche Vorgehensweise des Einzelnen wird außer
acht gelassen. Abbruchkriterien für den Lauf eines Individuums sind:
136
12.4 Bewertungsfunktion
• Zeit. Ein Individuum hat nur eine bestimmte ( festgelegte ) Anzahl Ticks zum
Lösen des Problems zur Verfügung.
• Kollision. Es wurden hinsichtlich der Kollisionsbehandlung zwei Möglichkeiten
untersucht. Zum einen wird der Test fortgesetzt, die Kollision wird aber mit
schlechterer Bewertung bestraft. Die andere Möglichkeit ist der Abbruch des
Durchlaufs im Falle einer Kollision. Die Ergebnisse werden später besprochen.
• Erreichen eines Optimums. Der Durchlauf wird abgebrochen, wenn ein optimaler Fitnesswert erreicht wird. Dies erleichtert die Konvergenz, schränkt aber
die Wiederverwertbarkeit ein. Dieses Abbruchkriterium wurde wieder entfernt.
Siehe dazu das Kapitel 12.9 Abbruchkriterium „Optimum erreicht“.
Die Bewertung setzt sich aus dem Abstand des Fahrzeugs in X- und Y-Richtung
vom Ziel sowie der Abweichung von der idealen Ausrichtung zusammen.
Die Gewichtung der einzelnen Komponenten ist für den Erfolg von großer Bedeutung. Daher wurden verschiedene Funktionen unter verschiedenen Konfigurationen
getestet.
Da die Bewertung immer einen positiven Wert haben muss, ist es sinnvoll, entweder den Absolutwert der Abweichung heran zu ziehen oder aber eine alternative
Behandlung zu finden. Die Bewertung soll nicht nur die Erreichung der Zielposition genau beschreiben, sondern eine möglichst gute Unterscheidung zwischen einem
guten Versuch und einem schlechten ermöglichen. Sind hier die Bestandteile falsch
gewichtet, wird eine Konvergenz deutlich erschwert.
Möglicherweise existieren im Suchraum ausgeprägte lokale Extremwerte, aus denen
es durch die verwendeten evolutionären Verfahren keinen oder nur unwahrscheinlich
erreichbare Auswege gibt.
Im Folgenden soll eine Bewertungsfunktion experimentell geschaffen werden, die
möglichst gute Ergebnisse erzielt. Als Ausgangsbasis für diese Entwicklung wird
zunächst die einfachste Bewertung hergenommen:
BewertungX =Abs(AbweichungX)
BewertungY =Abs(AbweichungY)
BewertungR =Abs(AbweichungR)*180
Abs(x) ergibt den Betrag von x. Die Bewertungen werden nach X und Y und R,
der Verdrehung, aufgeschlüsselt. Um die endgültige Bewertung zu erhalten, werden
137
12 Einparken ohne Anhänger
diese drei Komponenten addiert. Die Abweichungen in X- bzw. Y-Richtung werden
in „Einheiten“ gemessen.
Zur Erläuterung: ein Feld der „Welt“ ist jeweils 100 Einheiten breit und hoch. Das
Fahrzeug misst 60*40 Einheiten. Mit jedem Tick bewegt sich das Fahrzeug um einen
Vektor der Länge 4 Einheiten. In der angesetzten Zeit von 50 Ticks kann sich das
Fahrzeug also um 200 Einheiten bewegen.
Die Startkoordinaten variieren situationsbedingt. Sie liegen ungefähr bei X = 150
und Y = 100 Einheiten vom Zielpunkt entfernt. Damit liegen auch sehr schlechte
Werte nie über 500.
Die Strafe für die Abweichung von der erwünschten Ausrichtung beträgt hier 1 Punkt
pro Winkelgrad.
Ohne auf einzelne Durchläufe näher einzugehen lässt sich feststellen, dass die Vielzahl ähnlich guter Bewertungen aus verschiedenen Endpositionen die Konvergenz
erschweren. Die große Zahl an lokalen Extremen und die deutlich zu schwache Bestrafung der Komponente „Ausrichtung“ machen diese Bewertung nicht wirklich praktikabel. Auch eine Erhöhung der Bewertung der Ausrichtung durch Multiplikation
wie beispielsweise
BewertungR = Abs(AbweichungR)*180*4
führt zu keiner spürbaren Verbesserung.
Es zeigt sich, dass auch in der Abstandsbewertung Veränderungen notwendig sind.
Diese sollte wesentlich härter bestraft sein, wenn der Abstand größer ist. Bei geringen
Abweichungen zum Ziel soll die Bestrafung dagegen deutlich schwächer ausfallen.
Dies lässt sich dadurch erreichen, indem statt des Absolutwertes das Quadrat des
Abstandes verwendet wird. Die neuen Bewertungen sehen daher wie folgt aus:
BewertungX = Pow( AbweichungX, 2 )
BewertungY = Pow( AbweichungY, 2 )
Pow(x,n) ist eine Funktion, die die n-te Potenz von x berechnet.
Versuche ergeben ein rasches Anfahren des Ziels in fast jedem Durchlauf. Dabei wird
die Ausrichtung jedoch außer acht gelassen, so dass das Ergebnis nicht zufrieden
stellend ist.
Im Folgenden wird die Rotationsbewertung des Fahrzeugs daher durch Verwendung
der Funktion
BewertungR = Pow(AbweichungR*10,2 )
138
12.4 Bewertungsfunktion
verstärkt. Kleine Abweichungen von der Zielausrichtung werden dadurch nur schwach
bewertet, während größere Abweichungen zu deutlichen Strafen führen.
Auch hier wird wieder eine Reihe von Versuchen durchgeführt.
Das Ergebnis dieser Versuche ist, dass diese Bewertung immer noch Schwächen hat.
Die Strafe für Abweichungen vom Ziel wächst sehr schnell. Es könnte die Lösungsfindung erleichtern, einen besseren Kompromiss zwischen Rotation und Position zu
finden.
Es werden daher die Auswirkungen einer Abschwächung der Bewertung der Position
bei gleichzeitiger Verstärkung der Bewertung der Ausrichtung untersucht.
BewertungX = Pow( AbweichungX/2, 2 )
BewertungY = Pow( AbweichungY/2, 2 )
BewertungR = Pow( AbweichungR*30, 2 )
Hier zeigt sich vor allem bei geringen Ausrichtungsunterschieden die Dominanz der
Position. Wurde eine akzeptable Lösung gefunden, die das Fahrzeug auf den Zielpunkt steuert, dabei jedoch eine Verdrehung verursacht, kann diese nur schwer zu
Gunsten der Ausrichtung verändert werden, da die meist schlechtere Position mehr
Bewertungspunkte erhält als durch die Verbesserung bei der Rotation eingespart
werden kann.
Erhöht man die Bewertung der Ausrichtung um den Faktor 10 auf
BewertungR = Pow( AbweichungR*30, 2 )*10
werden in den meisten Fällen sehr gute Ergebnisse erzielt. Die thoretische Höchstpunktzahl von 0 bzw. eine Fitness von 1000 wird jedoch kaum jemals erreicht. Dies
hängt damit zusammen, dass das Fahrzeug nur eine begrenzte Anzahl Ticks zur
Lösung des Problems zur Verfügung hat. Es ist jedoch nicht möglich, vorher abzuschätzen, wie viel Zeit tatsächlich benötigt wird.
Daher ist es nicht nur möglich, sondern sogar wahrscheinlich, dass das Fahrzeug das
vorgegebene Ziel verfehlt und die beste, tatsächlich erreichte Lösung vom theoretischen Optimum abweicht. Unter „Abbruchkriterien“ wird eine Möglichkeit beschrieben, trotzdem das bestmögliche Ergebnis zu erzielen.
Das Erreichen der Optimallösung wäre für den Abbruch der Evolution wünschenswert, da hierdurch, auch in Hinblick auf spätere Versuche, längere Versuchsreihen
erheblich beschleunigt werden könnten.
139
12 Einparken ohne Anhänger
Um trotz der wechselnden Ausgangsbedingungen optimale oder zumindest sehr gute
Ergebnisse erreichen zu können, wird der Parkplatz großzügiger definiert. Dies stellt
einen gewissen Verzicht auf Präzision zu Gunsten der praktischen Nutzbarkeit dar.
Das Ziel ist im Folgenden nicht mehr nur ein Punkt, sondern eine Fläche, deren
Mittelpunkt dem bisherigen Ziel entspricht. Diese Fläche wird mit 10*10 Einheiten
definiert. Auch bei sich deutlich verändernden Ausgangsbedingungen sollte so eine
(annähernde) Optimallösung erreichbar sein.
Hierzu wird vor der Anwendung der oben zuletzt definierten Bewertungsfunktion
„5“ vom Betrag der Abweichung in X- und Y-Richtung abgezogen. Eine Abweichung
von 0 kann dabei nicht unterschritten werden.
Auch die Bewertung der Verdrehung wird so abgeändert, dass Winkel unter 5 Grad
als optimal angesehen werden.
Hierzu werden 5/180 vom Betrag der Rotation abgezogen. Die Abbildung 12.1 zeigt
eine mögliche Endposition bei erreichen der optimalen Fitness.
Abbildung 12.1.: Fitness 1000
Einige Ergebnisse eines Testlaufes mit der zuletzt entwickelten Bewertung unter
Anwendung der Zieltoleranz sahen, mit den Standard-Konfigurationen, wie folgt
aus:
140
12.4 Bewertungsfunktion
Generationen
Fitness
90
1000
100
90.90
100
500
30
1000
15
1000
43
1000
100
500
100
500
29
1000
Tabelle 12.2.: Testergebnisse bei Standardkonfiguration
In den meisten Fällen lässt sich das Erreichen der Optimallösung beobachten.
Problematisch ist oftmals die letzte kleine Verbesserung von Bewertungen wie 1 oder
2 hin zur 0. Dies ist aus dem Aufbau der Codierung deutlich erkennbar. Durch die
Verwendung der Werte der Reihe nach haben frühere Positionen größeren Einfluss
auf das Gesamtergebnis. In den ersten Stellen entscheidet sich, ob das Individuum
überhaupt eine Chance hat, das Problem zu lösen. Die Feinabstimmung erfolgt im
Endbereich des Gens. Hier kann das Ergebnis noch geringfügig verbessert werden.
Ist ein sehr guter Fitnesswert erst erreicht, kann sich kein Individuum mehr durchsetzen, das an dem Anfangsteil der Gen-Sequenz Änderungen vornimmt. Geschieht
es, dass auf Grund der Anfangsphase das Erreichen der Bestlösung ausgeschlossen
ist, wird dieses auch im Folgenden nicht mehr möglich sein. Alle Mutationen sind
dann schlechter als ihre Vorfahren. Gleichzeitig verarmt das genetische Material zunehmend, wodurch auch durch CrossOver kaum noch Verbesserungen zu erwarten
sind.
Es wäre natürlich möglich, die Trefferfläche weiter zu vergrößern und somit das Erreichen eines Abbruchkriteriums zu erleichtern. Eine derartige Vorgehensweise stößt
aber früher oder später an die Grenzen der praktischen Einsetzbarkeit, da diese
durchaus auch enge Grenzwerte erfordern kann.
Um die Ergebnis-Qualität zu verbessern, bietet es sich an, die Zielfläche gering zu
halten und stattdessen die Einparkzeit zu variieren. Um das Ende der Bewegung
leichter im definierten Bereich zu erreichen und somit schneller eine Lösung für das
gestellte Problem zu erhalten kann die Zielfläche hingegen vergrößert werden.
Es wäre durchaus möglich, die zur Verfügung stehende Zeit ebenfalls genetisch zu
optimieren. Im Falle der Codierung Vektor würde das dynamische Gen-Längen erfordern, die wesentliche Änderungen verschiedener genetischer Operationen mit sich
bringen würden. Um den Aufwand der Entwicklung in einem akzeptablen Rahmen
zu halten, wurde auf diese Option daher von Beginn an explizit verzichtet.
Als Kompromiss lässt sich die Zeit aber auch durch die EAServer-Konfiguration ver-
141
12 Einparken ohne Anhänger
ändern. Die eingestellte Knotenanzahl entspricht quasi der Zeit, die der Fahrer zur
Verfügung hat. Falls bei einer bestimmten Ausgangssituation ein unüberwindbarer
Höchstwert entsteht, kann man die Knotenzahl leicht variieren, um möglicherweise
bessere Ergebnisse zu erzielen.
Auch auf Seite der Simulation lässt sich die Einparkzeit konfigurieren. Hier kann
über den Konsolenbefehl „time“ eine Höchstzeit eingestellt werden. Liegt diese unter der konfigurierten Knotenanzahl, so werden überschüssige Knoten abgeschnitten.
Es gibt - durch geeignete Nutzung der Parameter des EAServers - noch weitere
Möglichkeiten, die Ergebnisse zu verbessern. Einige davon werden in den folgenden
Kapiteln auf ihren Nutzen hin untersucht.
Soll eine Lösung möglichst rasch gefunden werden, ohne dass diese zwingend „optimal“ ausfallen muss, kann der Konvergenzwert als Stellschraube für die Toleranz
verwendet werden. Bereits bei Fitnesswerten über 40, also Bewertungen, die besser
als 25 sind, kann das Fahrzeug als „eingeparkt“ angesehen werden. Die Abbildungen
12.2 zeigen mögliche Endpositionen bei einer Fitness von 20 bzw. 40.
Abbildung 12.2.: Fitness 20 bzw. Fitness 40
12.5. Bedeutung der Populationsgröße
Die Populationsgröße ist eine der wichtigsten Stellschrauben bei genetischen Algorithmen. Sie sorgt für Vielfallt, Konkurenz und erhöht die Wahrscheinlichkeit einen
guten Ansatz in der ersten Generation zu finden.
Sie erhöht aber auch den Rechenaufwandt einer Generation, da jedes Individuum,
142
12.5 Bedeutung der Populationsgröße
unabhängig von der Populationsgröße die gleiche Zeit benötigt. Es ist daher zu erwarten, dass es hier eine Grenze gibt, an der Lösungen am schnellsten gefunden
werden können.
Um die Bedeutung der Populationsgröße für die Geschwindigkeit der Lösungsfindung beurteilen zu können, werden einige Versuchsdurchläufe mit verschiedenen
Populationszahlen durchgeführt. Dabei soll sich zeigen, ob sich eine Vergrößerung
der Population auf Kosten der Rechenzeit einer Generation auszahlt.
Dabei soll die Möglichkeit zum Vergleich mit anderen Parametern gegeben sein.
Die Versuchsreihe mit 20 Durchgängen wurde zunächst ohne Generationengrenze
durchgeführt. Da jedoch bereits der erste Lauf auch nach 500 Generationen kein
optimales Ergebnis abliefern konnte, wurde entschieden, die maximal mögliche Anzahl Generationen auf 100 festzulegen. Dies führt allerdings zur Verfälschung der
Auswertung, da die tatsächlich benötigte Zeit, die sich aus Generationenzahl und
Populationsgröße zusammensetzt, durch die Grenze bei 100 für kleine Populationszahlen deutlich kleiner ausfällt als sie ohne Höchstwert würde.
Es ergeben sich die folgenden durchschnittlichen Generationen bis zur Konvergenz:
Populationszahl
Generationen
50
96
100
68.2
200
41.15
500
18.25
1000
8.3
2000
6.35
5000
5.8
Tabelle 12.3.: Durchschnittliche Zeiten bei unterschiedlichen Populationsgrößen
Dass das Ergebnis bei einer Populationsgröße von 50 nicht gut ausfallen würde, war
zu erwarten. Von den 20 Ausführungen fanden 2 die Lösung vor Erreichen der Generationengrenze. Die noch im Zeitrahmen erreichten Werte liegen in den meisten
Fällen über 20, so dass unter Anwendung einer gewissen Toleranz durchaus Lösungen gefunden werden können. Die Evolution steuert schnell auf einen guten Wert
zu, der in der verbleibenden Zeit keine große Änderung mehr erfährt. Es können
im Entwicklungsverlauf oftmals Stufen beobachtet werden, die meistens ein lokales
Extremum oder das Verarmen des genetischen Materials kennzeichnen. In diesen
Fällen kann es nach einigen weiteren Generationen wieder zu kleinen Verbesserungen kommen. Diese sind mutationsbedingt und bringen die Evolution nicht wirklich
wieder in Gang.
Dass die Werte nach kurzer Zeit nicht mehr deutlich besser werden, liegt hauptsächlich an der schnellen Verarmung der genetischen Vielfalt. Die Hauptoperation
143
12 Einparken ohne Anhänger
aller genetischen Verfahren ist das CrossOver, welches zwei Gene durch Austauschen
einzelner Informationen vereint. Bei geringer Populationsgröße ist der Konkurrenzdruck höher. Ein Individuum mit hoher Bewertung kann sich sehr leicht durchsetzen
und seine Gene in der nächsten Generation festigen. So kann ein Ausreißer in kürzester Zeit alle anderen genetischen Wurzeln aus der Population verdrängen. Nach
einigen Generationen sind alle Individuen genetisch Identisch, so dass der Einsatz
des CrossOver zu keinen Änderungen mehr führen kann.
Die Mutations-Wahrscheinlichkeit von 4% führt zu einer Veränderung von durchschnittlich 2 Genen in jeder Generation. Mindestens Eines davon muss stark genug
sein, um für ein CrossOver ausgewählt zu werden. Nur in diesem Fall könnte eine Verbesserung eintreten. Selbst wenn das Individuum es schaffen sollte, in der
Nachfolge-Generation mit einem Nachkommen vertreten zu sein, muss sich dieser
gegen eine große Anzahl genetisch identischer Konkurrenten durchsetzen. Es kommt
vor, dass eine Verbesserung nur ein oder zwei Generationen lang Bestand hat, bevor
diese Linie ausstirbt und die Fitness wieder auf den vorherigen Wert zurückfällt.
Bei so geringen Populationsgrößen ist also auch eine Entwicklung durch Mutation
sehr unwahrscheinlich.
Das Ergebnis der Populationsgröße 100 unterscheidet sich deutlich vom vorherigen
mit 50. Die erreichten Ergebnisse liegen insgesamt deutlich besser. Die optimale Lösung wurde in 9 von 20 Fällen gefunden, also 4 mal so häufig.
Nimmt man die erreichte Durchschnittszeit und macht sie vergleichbar mit der von
50 Individuen erreichten, indem man sie mit 2 multipliziert, stellt man fest, dass
die größere Population zu deutlich höherem Rechenaufwand führt, nämlich 136.4
gegenüber 96 Generationen. Vergleiche Tabelle 12.3.
Dies liegt, wie bereits erläutert, an der definierten Generationenhöchstzahl, welche
die Evolution teilweise mitten im Prozess beendet und den Wert niedriger Populationszahlen kleiner erscheinen lässt.
Die besseren Ergebnisse werden durch mehrere Faktoren erreicht. Zum einen ist
die Ausgangspopulation größer. Dadurch sind mehr verschiedene Grundansätze gegeben, die sich entwickeln können. Der Konkurrenzdruck nimmt ab, wodurch auch
schwächere Individuen Nachkommen haben können. Dies verbessert den genetischen
Varianzerhalt über mehrere Generationen.
Der letzte Grund ist die erhöhte Zahl mutierter Gene. Bei gleicher Mutationswahr-
144
12.5 Bedeutung der Populationsgröße
scheinlichkeit von 4% werden nun im Schnitt 4 Individuen vor Aufnahme in die
nächste Generation verändert. Hierdurch ergibt sich eine etwas längere Entwicklungsphase, bevor die genetische Varianz erschöpft ist. Dies geschieht weiterhin und
führt auch nach wie vor zu den oben beschriebenen Problemen. Deutlich erkennbar
wird dies bei Betrachtung der Konvergenzzeiten der erfolgreichen Durchläufe. 7 von
9 benötigten zur Konvergenz weniger als 30 Generationen. Die beiden Übrigen haben es nach langer Stagnation durch den Zufall der Mutation noch zu einer Lösung
gebracht. Der eine Durchlauf erreichte nach 15 Generationen die Fitness 500 und
schaffte den Sprung auf 1000 erst 40 Generationen später. Der andere erfuhr eine
langsame Entwicklung bis zur Generation 40 wo er eine Fitness von 333 erreichte.
Er hielt dann 20 Generationen lang diesen Wert um sich dann auf 500 zu verbessern.
Weitere 15 Generationen später gelang dann der Schritt auf die 1000.
Diese Entwicklung lässt vermuten, dass weitere Erhöhungen der Populationsgröße die frühe Konvergenz verbessern, während durch Erhöhung der Mutationswahrscheinlichkeit die genetische Verarmung unterbunden und somit die Befreiung aus
Extrema erleichtert werden kann.
Auch mit 200 Individuen in der Anfangs-Generation lässt sich eine weitere Steigerung beobachten. Von den 20 Durchläufen blieben 4 ohne Ergebnis. Von den 16
Erfolgreichen benötigten 10 weniger als 20 Generationen. Was immer deutlicher zu
beobachten ist, ist die Stagnation der ergebnislosen Durchläufe: teilweise treten 60
Generationen auf ohne Verbesserung.
Die Abbildung 12.3 zeigt den typischen Verlauf einer Erfolgreichen Lösungssuche.
Auffällig ist die lange Stagnation bis zum Sprung auf 1000. Die Abbildung 12.4 zeigt
zu dem selben Durchlauf den durchschnitlichen Fitnesswert der jeweiligen Generationen. Es ist zu erkennen, dass der Durchschnittswert dem Bestwert rasch folgt.
Dies ergibt sich durch die Verarmung des genetischen Materials.
Die Vergleichbarkeit der für die Berechnung verbrauchten Zeit wird durch Multiplikation der durchschnittlichen Generationenzahl mit 4 erreicht. Der Wert von 164.6
liegt höher als die beiden vorherigen. Es gilt auch hier die Aussage, dass diese Werte wegen der Höchstgrenze nur eingeschränkt vergleichbar sind. Um dennoch eine
Vorstellung von der Zeitersparnis zu bekommen, kann man nach 100 Generationen
nicht konvergierte Durchläufe statt mit 100 höher anrechnen. Verwendet man z.B.
1000 für die nicht konvergierten, so ergeben sich als Tatsächliche Zeiten: 906 für 50,
145
12 Einparken ohne Anhänger
Abbildung 12.3.: Beste Fitness der jew. Generation
Abbildung 12.4.: Durchschnittliche Fitness der jew. Generation
1126.4 für 100 und 884.6 für 200 Individuen je Generation. Auch diese Werte sind
nur mit Vorbehalt zu betrachten, da sie jedem Durchlauf unterstellen, dass er kein
Ergebnis nach 1000 Generationen finden würde, wenn er es nach 100 noch nicht hat.
Dennoch sind diese Zahlen zum Aufwandsvergleich besser geeignet als die anderen.
Insgesamt bestätigt die Populationsgröße 200 die Annahme, dass Durchläufe zwar
im Allgemeinen besser konvergieren, falls aber die genetische Varianz erschöpft ist,
wird das Finden einer Lösung fast unmöglich. Mit 8 Individuen schafft die Mutation
zwar mittlerweile eine gute Auffrischung, durch die große Anzahl genetisch identischer Konkurrenten kann sich eine Mutation jedoch nur dann behaupten, wenn sie
sehr gute Fitnesswerte erreicht. Da die Verarmung meist jedoch auf Fitnesswerten
über 200 geschieht ist eine solch deutliche Erhöhung ohne anschließenden Rück-
146
12.5 Bedeutung der Populationsgröße
schritt fast nicht möglich.
Es wäre daher erstrebenswert, solche Verarmung zu unterbinden oder wenigstens
guten jedoch isolierten Mutationen die Möglichkeit zu geben, sich durchzusetzen.
Hierzu werden später Populationsmodelle unter Verwendung von Eliten überprüft.
Bei 500 Individuen ergeben sich sehr gute Ergebnisse. Unter den 20 Durchläufen war
eine, die kein Ergebnis erbringen konnte. Mit der achten Generation wurde ein Fitnesswert von 333 erreicht, der nicht weiter verbessert werden konnte. Solche Läufe
sind hier die Ausnahme. 18 der Durchläufe benötigten weniger als 20 Generationen.
In 6 Fällen wurden 10 oder weniger Generationen benötigt. Es zeigt sich hier noch
deutlicher, dass das Verarmen der genetischen Vielfalt ein gewaltiges Hindernis für
die laufende Evolution darstellt. Die hohe Populationsgröße ermöglicht es jedoch,
frühzeitig Lösungen zu finden, bevor die genetische Verarmung einsetzen kann. Mit
einer tatsächlichen Zeit von 632.5 können die Lösungen normalerweise recht schnell
gefunden werden. Es ist zu erwarten, dass sich dieser Wert durch weitere Erhöhung
der Populationsgröße noch verbessern lässt, falls die ergebnislosen Durchläufe dadurch beseitigt werden können.
Bei einer Populationszahl von 1000 kann das Erreichen der Optimallösung beinahe
garantiert werden. Auch die Geschwindigkeit, mit der diese gefunden wird, kann
überzeugen. 13 der 20 Durchläufe benötigten weniger als 10 Generationen, kein
Durchlauf mehr als 12. Beim korrigierten Vergleich ergibt sich eine tatsächliche Zeit
von 166, was eine deutliche Steigerung gegenüber 500 Individuen darstellt.
Der schnellste Lauf benötigte nur 4 Generationen. Es stellt sich hier nun die Frage,
wie komplex das Finden einer Lösung tatsächlich ist.
Würde man versuchen, eine Lösung durch rein zufälliges Generieren zu erhalten,
hätte man keine Erfolgsaussichten. Dies zeigt sich deutlich beim Betrachten der Ausgangspopulationen. Alle Individuen werden zufällig generiert und keines der 20000
erzeugten Gene erreicht von Anfang an Werte über 10.
Von nun an kann man annehmen, dass sich die tatsächliche Geschwindigkeit des
Algorithmus bis zur Findung einer Lösung nicht durch weiteres Erhöhen der Populationsgröße steigern lässt. Zwar wird eine weitere Verbesserung der Konvergenzeigenschaften erwartet, der Mehraufwand wird sich jedoch voraussichtlich nicht
lohnen.
147
12 Einparken ohne Anhänger
Wie erwartet, sind die Ergebnisse bei 2000 Individuen sehr gut. Es gibt nur noch
eine geringe Varianz, so dass nicht nur die Lösungsfindung sondern auch eine zu erwartende Generationenzahl garantiert werden kann. Der langsamste Lauf benötigte
9, der schnellste 4 Generationen. Die meisten benötigten 6 oder 7 Generationen.
Die tatsächliche Zeit ist, wie zu erwarten war, mit 254 langsamer als mit 1000 Individuen. Eine Erhöhung über 1000 lohnt sich für dieses Problem also nicht.
Die Abbildung 12.5 zeigt den typischen Verlauf einer erfolgreichen Lösungssuche. Vor
dem Sprung auf 1000 liegt die Fitness bei 66. Die Abbildung 12.6 zeigt zu dem selben Durchlauf den durchschnitlichen Fitnesswert der jeweiligen Generationen. Der
Durchschnittswert steigt mit dem Bestwert. Dies geschieht hier jedoch wesentlich
langsamer als bei niedrigeren Populationszahlen. Zur siebten Generation lag dieser
Wert bei 6.18, der Bestwert bei 66.
Abbildung 12.5.: Beste Fitness der jew. Generation
Weitere 40000 zufällig generierte Gene ohne Lösung auf Anhieb unterstreichen die
Komplexität des Problems. Das beste Individuum hatte in Generation 1 eine Bewertung von 16. Damit fährt es bereits in die Parklücke, wobei Position und Ausrichtung
in weiteren Generationen noch deutlich verbessert werden konnten.
Auch wenn keine Verbesserung mehr zu erwarten ist, wird die Populationsgröße auf
5000 gesteigert. Es ist zu erwarten, dass sich die durchschnittliche Konvergenzzeit
auf unter 6.0 verbessert. Da aber kaum mit Ausreißern unter 4 Generationen zu
rechnen ist dürfte die tatsächliche Zeit im Bereich der 500 Individuen liegen.
Nach diesem Testlauf bestätigt sich die Erwartung. Das Verwenden von 5000 In-
148
12.6 Die Bedeutung der Mutations-Wahrscheinlichkeit
Abbildung 12.6.: Durchschnittliche Fitness der jew. Generation
dividuen ist nicht rentabel. Für die Aufgabe „Einparken ohne Anhänger“ kann auf
Versuche mit solch hohen Populationszahlen verzichtet werden. Daher werden auch
spätere Versuchsreihen ohne 5000, zumeist auch ohne 2000 stattfinden. Es ist zu
erwarten, dass diese Populationszahlen für das Einparken mit Anhänger wesentlich
bedeutender sind.
Es bleibt noch festzustellen, dass auch die hier erzeugten 100000 Chromosomen in
der ersten Generation keine Lösung erbringen konnten. Bei einer Suchraumgröße von
6050 wurden ca. 200000 Chromosomen erzeugt. Dies entspricht 2.47 ∗ 10−83 % des
Suchraums. Insgesamt wurden 1579500 Chromosomen auf ihre Eignung als Lösung
untersucht.
Ein gewisser Anteil davon waren wiederholt bewertete Fahrer. Damit wurden 118
Lösungen in 1.94 ∗ 10−81 % des Suchraumes gefunden. Bei solchen Zahlen werden
die Vorzüge der genetischen Verfahren immer deutlicher.
12.6. Die Bedeutung der
Mutations-Wahrscheinlichkeit
Die Mutations-Wahrscheinlichkeit beschreibt, wie wahrscheinlich es für ein einzelnes
Individuum ist, mutiert zu werden. Die Mutation ist ein wesentlicher Bestandteil
der Evolution, sollte jedoch im Allgemeinen gering ausfallen. Zu starke Mutation
kann dazu führen, dass die Unterschiede zwischen den Generationen zu groß werden
149
12 Einparken ohne Anhänger
und nicht nachvollziehbare Evolutionssprünge entstehen. Die in dem EAServer implementierte Mutation wendet die Mutations-Wahrscheinlichkeit auf jedes einzelne
Chromosom an. Wurde ein Chromosom als zu mutieren ausgewählt, werden feste
Mutationsregeln angewandt. Alternativ hätte die Mutationswahrscheinlichkeit für
jede Stelle jedes Chromosoms angewendet werden können. Es wäre dann nur diese
Stelle verändert worden. Dieses Vorgehen hätte den Vorteil gehabt, dass eine größere Zahl von Chromosomen mutiert würden, dafür ist die Änderung aber deutlich
schwächer. Dieses Verfahren konnte aufgrund der Codierung Car, die eine Baumstruktur verwendet, nicht eingesetzt werden.
Um Vergleiche zu ermöglichen, wird der Test jeweils mit einer Populationsgröße von
100 und 200 durchgeführt. Bei 100 Individuen ist rasche Verarmung zu beobachten,
so dass die meisten Durchläufe von der Mutation abhängen. Bei einer Populationsgröße von 200 erreichen fast alle Durchgänge eine Lösung.
Im Folgenden soll untersucht werden, ob die wenigen Ausnahmen durch höhere
Mutations-Wahrscheinlichkeiten noch beseitigt werden können.
Die Versuche laufen jeweils mit 4%, 8%, 15% und 25%.
Für 4% werden die Ergebnisse von oben übertragen.
Mutations-Wahrscheinlichkeit
Generationen
4%
68.2
8%
80.45
15%
61.7
25%
55.15
Tabelle 12.4.: Durchschnittliche Konvergenzzeit bei Populationsgröße 100
Mutations-Wahrscheinlichkeit
Generationen
4%
41.15
8%
34.25
15%
31.9
25%
23.85
Tabelle 12.5.: Durchschnittliche Konvergenzzeit bei Populationsgröße 200
Das Ergebnis zu 8% Mutationswahrscheinlichkeit bei 100 Individuen ist nicht deutlich anders als bei 4%. Zwar fällt es schlechter aus, die Ursachen und Beobachtungen
sind jedoch die gleichen. Nach einer Anfänglichen Phase der guten Entwicklung verarmt das genetische Material, wodurch kaum noch Verbesserung möglich ist. Durch
die gesetzte Obergrenze fuer die Anzahl der Generationen ist nicht zu erkennen, ob
im späteren Verlauf deutliche Verbesserungen erfolgen. Der rechnerisch schlechtere
Wert wird an dieser Stelle dem Zufall zugeschrieben. 20 Durchläufe erlauben nur
150
12.6 Die Bedeutung der Mutations-Wahrscheinlichkeit
eine eingeschränkte Verallgemeinerung. Starke Schwankungen können also durchaus auftreten. Es wird sich zeigen, ob auch bei 200 Individuen oder bei größeren
Mutations-Wahrscheinlichkeiten Verschlechterung eintritt.
Bei 200 Individuen lässt sich mit 8% Mutations-Wahrscheinlichkeit eine Verbesserung beobachten. Hier traten 3 Läufe ohne Ergebnis auf, so dass sich nicht eindeutig
feststellen lässt, ob die Konvergenz der langen Läufe wie erwartet verbessert werden
konnte. Darüber können erst weitere Tests Aufschluss geben.
Mit 15% Mutations-Wahrscheinlichkeit für 100 Individuen konnte wieder eine Verbesserung gegenüber der von 8% beobachtet werden. Diese bringt die Durchschnittszeit jedoch nur auf das Niveau der 4%. Daher kann auch hieraus kein eindeutiger
Schluss gezogen werden. Es lässt sich im Verlauf der besten Fitness mehr Bewegung
erkennen als bei niedrigeren Mutations-Wahrscheinlichkeiten. Auch die Grafen für
die durchschnittliche Fitness und die Differenz zeigen mehr Bewegung. Diese deutet
auf eine höhere Varianz hin, was der Evolution auf jeden Fall zu gute kommt.
Bei 200 Individuen lässt sich mit 15% Mutations-Wahrscheinlichkeit eine weitere
Verbesserung der Geschwindigkeit beobachten. Diese ergibt sich jedoch nicht wie
erwartet aus einer Abschaffung der nicht konvergierenden Durchläufe, sondern aus
einer Verbesserung der frühen Entwicklung. Auch mit diesen Einstellungen erbrachten 3 von 20 Durchgänge keine Lösung. Zwar lässt sich deutliche Bewegung in den
durchschnittlichen Fitnesswerten erkennen, auf die stagnierende Entwicklung hat
dies jedoch nur eingeschränkten Einfluss.
Bei 25% und einer Populationsgröße von 100 ergibt sich eine weitere Verbesserung.
Insbesondere längere Verarmung kann durch die hohe Mutations-Rate unterbunden
werden. Ersichtlich wird die Auswirkung der Mutation bei Betrachtung der durchschnittlichen Fitness. Auch bei langer Stagnation der besten Fitness können hier
deutliche Änderungen beobachtet werden.
Die Reihe der Verbesserungen setzt sich für 200 Individuen auch mit 25% MutationsWahrscheinlichkeit fort. Es konnte nun nicht nur eine Verbesserung der allgemeinen
Konvergenzgeschwindigkeit, sondern auch der Konvergenz-Wahrscheinlichkeit beobachtet werden. Nur einer von 20 Durchläufen endete ohne Lösung. Damit ließ sich
151
12 Einparken ohne Anhänger
die Leistung des genetischen Algorithmus mit 200 Individuen etwa auf das Niveau
von 500 Individuen steigern. Es kann also von einem Zeitgewinn durch Erhöhung
der Mutations-Wahrscheinlichkeit gesprochen werden.
Insgesamt lässt sich für das Einparken ohne Anhänger kein wirklich großer Einfluss der Mutations-Wahrscheinlichkeit erkennen. Nur wenn ohnehin bereits gute
Lösungen gefunden werden, lässt sich über die Mutations-Wahrscheinlichkeit die
Geschwindigkeit der Konvergenz beeinflussen. Die erhoffte Beseitigung der raschen
Verarmung des genetischen Materials blieb weitestgehend aus. Zwar lässt sich eine
Verlängerung der Entwicklungsphase beobachten, welche die Konvergenzgeschwindigkeit verbessert, die problematischen langen Phasen der Stagnation ließen sich
jedoch nicht entfernen.
Im Rahmen der Versuche zum Einparken MIT Anhänger wird sich zeigen, ob die
Mutations-Wahrscheinlichkeit bei anderer Komplexität des Problems größere Bedeutung hat.
Möglicherweise hätten sich mit der alternativen Implementierung hier bessere Ergebnisse erzielen lassen.
12.7. Die Bedeutung von Eliten
Ein Parameter des EAServers beschreibt die zu verwendende Ersetzungsstrategie. In
den bisherigen Versuchen wurde hier der Standard „Generational“ verwendet. Dieser
ersetzt die alte Generation vollständig durch neuen Individuen. Dies führt dazu, dass
die Eliten, also die besten Individuen einer Generation, unter Umständen aussterben
ohne der Evolution gedient zu haben. Dies führt vor allem bei verarmtem Genmaterial dazu, dass sich Mutationen mit besseren Fitnesswerten nicht durchsetzen können
und somit dieser Verbesserungsansatz wieder ausstirbt. Dieses Phänomen lässt sich
immer wieder beobachten.
Die Ersetzungsstrategie „Elitism“ überträgt die besten Chromosomen in die nächste
Generation. Auf diese Art und Weise wird das Aussterben besserer Ansätze verhindert. Problematisch dabei ist, dass die Bewertung nicht uneingeschränkte Aussagen
über die Qualität eines Ansatzes zulässt. Es kann sein, dass eine scheinbare Verbesserung in einer evolutionären Sackgasse endet, aus der es durch reine Verbesserung
152
12.7 Die Bedeutung von Eliten
kaum einen Ausweg gibt. In diesem Fall könnte es von Vorteil sein, wenn - in begrenztem Umfang - Verschlechterung durch genetischen Rückschritt möglich wäre.
Der folgende Versuch soll zeigen, ob das Mitführen eines Elitisten die Konvergenzeigenschaften verbessert.
Hierzu wird als Referenz die obige Versuchsreihe herangezogen. Es werden weitere
Versuchsläufe mit 100, 200 und 500 Individuen durchgeführt. Dabei wird der Elitenprozentsatz jeweils so konfiguriert, dass genau ein Chromosom mitgenommen wird.
Es werden also der Reihe nach 1%, 0.5% und 0.2% eingestellt.
Populationszahlen
Generationen
100
76.35
200
29.3
500
11.15
Tabelle 12.6.: Durchschnittliche Konvergenzzeit mit Eliten
Dass die durchschnittliche Zeit zugenommen hat, kann bei 100 Individuen je Generation möglicherweise der normalen Schwankungsbreite zugeschrieben werden und
muss nicht zwingend durch die Verwendung von Eliten bedingt sein. Es lässt sich
daher allein aus diesem Ergebnis noch kein Schluss über den Nutzen von Eliten
ziehen. Was durchweg beobachtet wurde, ist, dass die Fitness beim Einsetzen der
Stagnation geringer war als ohne Eliten. Es ist möglich, dass durch die fehlende
Möglichkeit des Rückschrittes schneller ein Wert erreicht wird, der kaum noch zu
verbessern ist. Die Betrachtung der „best Fitness - average Fitness“-Grafen zeigt,
dass die Verarmung schnell eintritt. Dies ist auch ohne Eliten der Fall, so dass auch
hier dazu keine eindeutige Bewertung möglich ist. Die Untersuchungen mit 200 bzw.
500 Individuen werden weiteren Aufschluss geben.
Bei 200 Individuen lässt sich eine Verbesserung beobachten. Von den 20 Durchgängen blieb Einer ergebnislos. Durch das Mitnehmen des Besten aus einer Generation
in die Nächste, ließ sich die Durchschnittszeit auf das Niveau der Testläufe mit 500
Individuen ohne Eliten verbessern. Es scheint daher empfehlenswert, Eliten einzuschalten, wenn sich dieser Trend bei 500 Individuen bestätigt.
Die Ergebnisse mit 500 Individuen bestätigen die Leistungsverbesserung des Algorithmus durch die Ersetzungsstrategie „Elitism“. Ab einer gewissen Populationsgröße
scheint es Erfolg versprechender, Eliten einzuschalten.
153
12 Einparken ohne Anhänger
12.8. Kollision
In einer Reihe von Tests mit verschiedenen Parametern und Bewertungen hat sich
herausgestellt, dass es zu besseren Ergebnissen führt, den Lauf eines Individuums
zu beenden, sobald dieses gegen ein Hindernis stößt. Deutlich gezeigt hat sich dies,
wenn das Fahrzeug mehr Zeit zur Verfügung hat als es zum Einparken benötigt.
In diesem Fall neigt es dazu, wenn es die Optimallösung verpasst, auf das nächste
Fahrzeug aufzufahren. Es kann nun passieren, dass, obwohl die Lösung fast perfekt
ist, hohe Strafen entstehen, die diesen Versuch fast Wertlos machen. Wird das Fahrzeug allerdings bei Kollision gestoppt, kann es sich an die beste, so mögliche Lösung
herantasten. Daher sind auch alle weiteren Tests mit „Kollision führt zu Abbruch“
durchgeführt worden.
Das Kriterium „Kollision führt zu Bestrafunng“ könnte z.B. eingesetzt werden, wenn
man die Zeit, die ein Fahrzeug zur Verfügung hat, ebenfalls genetisch optimieren
möchte.
12.9. Abbruchkriterium „Optimum erreicht“
In der Planung der Simulation erschien es sinnvoll, die Fahrt eines Individuums zu
beenden, wenn dieser eine Fitness von 0, und damit die bestmögliche Lösung erreicht. Dabei wurde die reduzierte Wiederverwertbarkeit in Kauf genommen. Diese
ergibt sich daraus, dass durch Veränderungen der Startbedingungen der selbe Fahrer
andere Bewertungen erhält. Er passiert die 0 unter Umständen nicht, wird also auch
nicht abgebrochen und erzielt letztlich ein schlechteres Ergebnis.
Der Vorteil dieses Abbruchkriteriums ist die schnellere Konvergenz, da das Ziel nicht
exakt erreicht werden muss, sondern nur durchfahren.
Es hat sich im Verlauf der Testphase gezeigt, dass die letzte Verbesserung zum Optimum oft in einem großen Sprung geschieht oder aber ganz ausbleibt. Nach einigen
Überlegungen wurde klar, dass dieses Abbruchkriterium dafür verantwortlich ist.
Durch die begrenzte verfügbare Zeit eines Fahrers kann es vorkommen, dass das
Ziel von einem Startpunkt aus nicht erreichbar ist. In diesem Fall ist kein Optimum
154
12.9 Abbruchkriterium „Optimum erreicht“
möglich. Durch das Abbruchkriterium des Erreichens des Fitnesswertes 0 kann es
vorkommen, dass ein Fahrer zufällig das Ziel durchfährt und damit die Bestlösung
bietet. Das Problem ist, dass die fließende Konvergenz damit gestört ist. Daher sind
die Evolutionsläufe mit diesem Abbruchkriterium nicht gut geeignet, um die Funktionsweise von Evolutionären Algorithmen umzusetzen.
Dieses Abbruchkriterium wurde daher wieder verworfen.
155
13. Einparken mit Anhänger
157
13 Einparken mit Anhänger
13.1. Erwartung
Einparken mit Anhänger ist eine wesentlich größere Herausforderung, sowohl für
Mensch als auch Maschine. Da die Manöver weniger ausgeprägt sind, benötigt der
Fahrer vermutlich mehr Zeit für das Einparken. Für die folgenden Tests wurden 6070 Ticks verwendet. Für die Größe des Suchraums ergeben sich hier also wenigstens
6060 oder 4.88 ∗ 10104 mögliche Chromosomen.
Außerdem ist zu erwarten, dass die Zahl der möglichen Lösungen deutlich geringer
ist als beim Einparken ohne Anhänger. Die Wahrscheinlichkeit, eine Lösung zufällig
zu finden, sinkt daher beträchtlich.
Beim Einparken mit Anhänger ist, im Gegensatz zum Rückwärtsfahren für das recht
schnell Lösungen gefunden werden konnten, eine kontrollierte Bewegung in eine seitliche Richtung erforderlich. Also muss zunächst der Anhänger in diese gedreht werden. Dann wird er möglichst gerade in die Parklücke geschoben und zum Schluss
müssen Anhänger und Fahrzeug wieder ausgerichtet werden. Es ist daher zu erwarten, dass der Zeitaufwand stark zunimmt.
13.2. Allgemeine Versuchsbedingungen
Solange in der Beschreibung nichts anderes geschildert wird, ist davon auszugehen,
dass die nachfolgende Standardkonfiguration verwendet wurde:
13.3. Bewertungsfunktion
Die Bewertung für das Einparken mit Anhänger wird aus der bereits erfolgreich
eingesetzten Bewertung für das Einparken ohne Anhänger abgeleitet. Die drei bereits
entwickelten Bestandteile bleiben unverändert.
Für den Anhänger wird die Bewertung um den folgenden Anteil erweitert:
BewertungA = Pow( AbweichungA*30, 2) *10.
Die Verdrehung des Anhängers wird also der des Fahrzeugs gleichgestellt.
Tests ergaben für diese Funktion keine überzeugenden Ergebnisse. Die Verdrehung
des Anhängers ist zwar meistens sehr gering, dafür aber die Verdrehung des GesamtGespanns recht groß.
158
13.3 Bewertungsfunktion
Populationsmodel
Populationszahl
Problem
Genlänge
UpperA
Crossover
CO Probability
Mutation
M Probability
Termination
Generation
Convergence value
Selection
Mating
Replacement
Serie mit 20 Durchläufen
500
Vehicle
65
3
One Point
100%
Equal
4%
Convergence & Generation
Maximum 100
1000
Roulette wheel
Random
Generational
Tabelle 13.1.: Standardkonfiguration
Die Fahrzeugausrichtung muss daher größeren Einfluss auf die Bewertung erhalten.
Der Faktor dieses Anteils wird im Folgenden auf 15 erhöht.
BewertungR = Pow( AbweichungR*30, 2) *15
Es ergeben sich bessere Ansätze, die jedoch noch nicht zu guten Ergebnissen ausreichen. Es kommt oft vor, dass die Endposition des Fahrzeugs stark vom Ziel abweicht.
Daraus lässt sich schließen, dass bei dieser Bewertung die Positions-Erreichung zu
schwach gewichtet ist.
Es werden daher die Bewertungs-Faktoren für die Verdrehung von Fahrzeug und
Anhänger reduziert.
BewertungR = Pow( AbweichungR*30, 2) *10
BewertungA = Pow( AbweichungR*30, 2) *5
Mit der somit veränderten Bewertung konnten gute Ansätze entwickelt werden. Im
Rahmen der Versuche zur Populationsgröße wird sich zeigen, ob auch gute Lösungen
gefunden werden können.
159
13 Einparken mit Anhänger
Im Rahmen der Versuchsreihe hat sich stärker als beim Einparken ohne Anhänger
die Bedeutung der Bewertungsfunktion gezeigt.
Ist diese schlecht gewählt, kann ein annehmbares Ergebnis nicht erwartet werden.
Es ist möglich, dass das gesetzte Ziel unter bestimmten Ausgangsbedingungen nicht
erreichbar ist. Es wurde festgestellt, dass dies beim Einparken mit Anhänger recht
häufig auftritt. Man kann daher sagen, dass die beste Lösung für ein Problem durch
die Bewertung nicht zwangsläufig zu erkennen ist.
Es ist möglich, die Wahrscheinlichkeit des Erreichens einer Bewertung von 0 - und
damit das Erkennen des besten Ergebnisses - zu erleichtern, indem die Zieltoleranz
vergrößert wird. Dies führt zwar zu einer wahrscheinlicheren Lösungsfindung und
erlaubt auch das Lösen problematischerer Situationen, erreicht wird dies jedoch auf
Kosten der Qualität der Lösung. Für das Einparken mit Anhänger erscheint ein
Vergrössern des Ziel-Streubereichs sinnvoll, da es weitaus wichtiger erscheint, überhaupt eine Lösung zu finden als Keine.
Dies lässt sich nicht auf jedes Szenario übertragen. Es kann je nach Problemstellung
vorkommen, dass das Setzen eines utopischen, unerreichbaren Ziels die Konvergenz
gegen ein sehr gutes Ergebnis beschleunigt. Auch wenn das Auffinden einer optimalen Lösung dadurch ausgeschlossen ist, lässt sich die Qualität der gefundenen
Ansätze dadurch steigern.
Wird die Bewertungsfunktion falsch gewählt, kann es auch vorkommen, dass die
beste erreichbare Bewertung keine zufriedenstellende Problemlösung hervorbringt.
Der wichtigste Vorteil einer definierten, erreichbaren Bestlösung ist im Bereich der
Abbruchkriterien zu finden. Wird der angestrebte Wert erreicht, endet die Evolution
und das Problem gilt als gelöst.
Ist der größte tatsächlich erreichbare Fitnesswert kleiner als der gewünschte Konvergenzwert, entfällt diese Beschleunigung des Verfahrens. Die Evolution schreitet
dann bis zum Abbruch durch z.B. Erreichen einer als Maximum definierten Anzahl
Generationen fort.
Es ist keinesfalls immer vorhersehbar, welche Ergebnisse möglich sind und wie das
beste Ergebnis zu definieren sein wird.
Im Verlauf der durchgeführten Versuche hat sich des weiteren gezeigt, dass die Startbedingungen einen großen Einfluss auf das zu erwartende Ergebnis haben.
Da die Parklücken erst erkannt werden, wenn das Fahrzeug auf einer zum Einparken geeigneten Position steht, variieren die Bedingungen sehr stark. Dies war bei
der Entwicklung zwar gewünscht, erschwert jedoch vergleichende Versuche. Beson-
160
13.4 Populationsgröße und Mutations-Wahrscheinlichkeit
ders die Position des Anhängers hat großen Einfluss auf das mögliche Ergebnis. Es
hat sich gezeigt, dass nicht in jeder geeignet scheinenden Situation auch wirklich
verwertbare Ergebnisse erzielbar sind.
Zur Sicherstellung der Vergleichbarkeit wurden alle Versuche mit exakt den selben Startbedingungen durchgeführt. Dies wurde erreicht, indem der Zufall aus dem
Pfadfinder-Algorithmus herausgenommen wurde. Außerdem wurde ein Szenario gewählt, das in vielen Fällen auswertbare Ergebnisse ermöglicht.
13.4. Populationsgröße und
Mutations-Wahrscheinlichkeit
Das Einparken mit Anhänger ist ein sehr komplexes Problem. In einem großen Suchraum existieren nur verhältnismäßig wenige Lösungen. Daher ist zu erwarten, das
nicht jedes Ausführen des evolutionären Algorithmus eine gute Lösung in vertretbarer Zeit hervorbringt. Die Wahrscheinlichkeit einer Konvergenz lässt sich, wie
bereits beim Einparken ohne Anhänger beschrieben, durch die Steigerung der Populationsgröße und der Mutations-Wahrscheinlichkeit vergrößern. Im Folgenden soll
versuchsweise ermittelt werden, welcher Parameter die besseren Ergebnisse hervorbringt.
Da, wie oben beschrieben, das Erreichen einer Optimallösung unwahrscheinlich ist,
wird eine Toleranz angewandt, die das Problem als gelöst ansieht, wenn der erreichte Fitnesswert besser als 100 liegt. Diese Toleranz findet zusätzlich zur definierten
Zielfläche Anwendung.
Populationsgröße 200 und Mutations-Wahrscheinlichkeit 4%
Mit diesen Einstellungen ergeben sich ca. 90 Generationen durchschnittliche Konvergenzzeit. Aus den 20 Durchläufen erreichten 3 den gesetzten Fitnesswert. Es ist
ersichtlich, dass diese Populationsgröße nicht geeignet ist, um für dieses Problem
Lösungen zu finden.
Populationsgröße 200 und Mutations-Wahrscheinlichkeit 15%
Der Versuch, die Mutations-Wahrscheinlichkeit bei gleicher Populationsgröße zu verändern, führte nicht zu besseren Ergebnissen. Daher wurden mit dieser Populations-
161
13 Einparken mit Anhänger
größe keine weiteren Tests durchgeführt. Die durchschnittliche Zeit liegt mit 87.3
nicht besser als vorher. Auch dass jetzt 4 der 20 Durchgänge konvergierten ist eher
als eine statistische Ungenauigkeit als eine Verbesserung der Konvergenzeigenschaften anzusehen.
Populationsgröße 500 und Mutations-Wahrscheinlichkeit 4%
Mit 84.15 Generationen bis zur Konvergenz liegt auch diese Konfiguration nicht besser als die bisherigen Versuche. 16 Durchläufe konnten kein Ergebnis erbringen. Der
durchschnittlich erreichte Fitnesswert der nicht konvergierten Durchgänge liegt mit
21.27 in einem recht guten Bereich.
Populationsgröße 500 und Mutations-Wahrscheinlichkeit 15%
Die Ergebnisse dieser Konfiguration liegen im selben Bereich wie bei der vorherigen.
Die Unterschiede sind auch hier noch zu gering, um eine eindeutige Auswertung zu
ermöglichen. Es bleibt anzunehmen, dass sich das Ergebnis durch eine weitere Steigerung der Populationszahl verbessern lässt.
Populationsgröße 1000 und Mutations-Wahrscheinlichkeit 4%
Auch hier liegt die Durchschnittszeit mit 83.5 im selben Bereich. Jedoch liegt der
durchschnittlich erreichte Fitnesswert mit 35.79 deutlich besser als in den anderen
bisher durchgeführten Versuchen.
Insgesamt konnte hier festgestellt werden, dass die konvergierenden Durchgänge in
den meisten Fällen deutlich weniger als 50 Generationen benötigen. Dies wird im
folgenden zur Beschleunigung der Versuche ausgenutzt, indem das Generationenlimit auf 50 reduziert wird. Dies führt allerdings dazu, dass die neuen Ergebnisse
nicht mit den bisher Erbrachten vollständig vergleichbar sind. Wesentliches Kriterium wird daher die Anzahl der gefundenen Lösungen sein.
Die Tests haben gezeigt, dass die Wahrscheinlichkeit, eine gute Lösung zu finden,
sehr gering ist. Es kann durchaus möglich sein, dass sich die Ergebnisse auch nach
Einsetzen der Stagnation noch verbessern können. Da der Zeitaufwand bis zu einer
möglichen Konvergenz aber extrem groß wird, wurde dies nicht vollständig untersucht. Das Problem des Einparkens mit Anhänger erfordert zum Erreichen brauchbarer Ergebnisse eine deutliche Steigerung der Populationszahlen. Aufgrund der ge-
162
13.5 Weitere Bewertungen
wählten Bewertung werden auch mit größeren Populationszahlen wie 2000 oder 5000
noch immer einige nicht konvergierende Durchläufe auftreten.
Dies liegt in erster Linie an der Prägung des späteren Ergebnisses in den ersten
paar Generationen. Nach dieser „Anfangsphase“ existiert im Grunde nur noch ein
Lösungsansatz, der im Bereich des Möglichen verbessert wird. Die einzelnen Werte
innerhalb des Chromosoms wiegen dabei unterschiedlich schwer.
Während kleine Änderungen in den frühen Vektorpositionen zu großen Änderungen der Fitness führen, können die letzten Werte nur noch geringe Verbesserungen
hervorbringen. Entsprechend lässt sich beobachten, dass die Verarmung des genetischen Materials dieser Gewichtung folgt. Zuerst bildet sich ein gemeinsamer Anfang
aus. Der gemeinsame Anteil wird dann mit der Zeit immer größer. Das Problem
an dieser Entwicklung ist, dass, wenn erst ein gemeinsamer Ansatz existiert, kein
anderer mehr die Chance hat, sich durchzusetzen. Da letztlich nur die Endposition
bewertet wird, ist es nicht möglich, bereits in einer Frühphase einen guten von einem
schlechten Ansatz zu unterscheiden.
Es wäre daher zu Überlegen, welche Möglichkeiten es gibt, das „Vorgehen des Fahrers“ anstelle des Endergebnisses zu bewerten.
13.5. Weitere Bewertungen
Die obigen Versuche wurden schließlich abgebrochen zugunsten weiterer Testläufe
mit - modifizierten - Bewertungsfunktionen.
Zunächst wird eine Bewertung untersucht, welche die Y-Abweichung am schwächsten gewichtet. Dadurch wird eine Verschiebung innerhalb der Parktasche weniger
bedeutend. Gleichzeitig wird die Y-Toleranz auf 10 erhöht.
BewertungX
BewertungY
BewertungR
BewertungA
=
=
=
=
Pow(
Pow(
Pow(
Pow(
AbweichungX/2, 2)*5
AbweichungX/2, 2)
AbweichungR*30, 2) *40
AbweichungR*30, 2) *20
Als Test wurde das Einparken zehn mal mit 1000 Individuen und 10 mal mit 2000
gelernt. Als Konvergenzwert wurde 20 eingestellt, was bei dieser Bewertung, wie aus
Abbildung 13.1 ersichtlich, recht gut ist.
163
13 Einparken mit Anhänger
Populationsgröße
Generationen
1000
35.8
2000
29.8
Tabelle 13.2.: Testergebnisse bei Bewertung 2
Abbildung 13.1.: Endposition mit Fitness 20 bei Bewertung 2
Die Generationengrenze wurde auf 50 eingestellt, um schneller beurteilen zu können, ob diese Bewertung zu guten Ergebnissen gelangt. Somit ist diese Testreihe nur
eingeschränkt mit der oberen vergleichbar.
Mit dieser Bewertung ist das Erreichen sehr guter Werte erschwert, dafür werden
häufiger Ergebnisse beobachtet, die als annehmbares Einparken gelten können. 4
von 10 bzw. 5 von 10 Durchgängen erreichten den Konvergenzwert und damit Ergebnisse, die wenigstens der Leistung der obigen Abbildung 13.1 entsprechen.
Auch hier gilt: Mit größeren Populationszahlen, anderem Populationsmodell und
viel Zeit lassen sich noch bessere Lösungen finden.
Trotz der recht hohen Bestrafung für Abweichungen in X-Richtung ist das Ergebnis in den meisten Fällen in Richtung Straße verschoben. Dies liegt an der Art der
164
13.5 Weitere Bewertungen
Entwicklung der Lösung. Durch die hohen Strafen für die Verdrehung des Fahrzeugs
bildet sich zunächst ein Ansatz heraus, der Fahrzeug und Anhänger gerade rückwärts fahren lässt. Dabei bewegt sich das Fahrzeug zwar in Richtung Parklücke,
erreicht diese jedoch meist nicht. Im Laufe der Evolution bewegt sich die Endposition bei gleichzeitigem Erhalt der Ausrichtung zunehmend weiter in die Parklücke.
Um dies zu beschleunigen könnte man das Ziel beispielsweise tiefer in die Parktasche
verschieben. Hier soll statt dessen eine weitere Bewertungsfunktion getestet werden.
Die Strafe für die Rotation von Fahrzeug und Anhänger scheint zu groß zu sein.
Daher wird im folgenden die X-Bewertung verstärkt. Die Rotation wird mit der
vierten Potenz, dafür aber mit geringerem Faktor bewertet.
BewertungX
BewertungY
BewertungR
BewertungA
=
=
=
=
Pow(
Pow(
Pow(
Pow(
AbweichungX/2, 2)*10
AbweichungX/2, 2)
AbweichungR*30, 3)*4
AbweichungR*30, 3)
Auch für diese Bewertung wurden die obigen Tests durchgeführt. Der Konvergenzwert liegt nun bei 50 was Ergebnisse erbringt, die im Bereich des in Abbildung 13.2
dargestellten liegen. Wird er geringer gewählt, ist die Verdrehung des Anhängers
meist zu groß.
Populationsgröße
Generationen
1000
39.4
2000
39.3
Tabelle 13.3.: Testergebnisse bei Bewertung 3
3 der 10 Durchläufe konvergierten wie gewünscht. Dies gilt jedoch in beiden Konfigurationen, so dass anzunehmen ist, dass die Populationszahl beträchtlich gesteigert
werden muss, um deutlich bessere Ergebnisse zu erhalten. Die Vorgehensweise der
Evolution ist hier durch die Gewichtungen gesteuert: erst in die Parklücke einfahren,
dies bereits so gut ausgerichtet wie möglich, jedoch durchaus auch stark verdreht.
Dann wird die Ausrichtung soweit möglich verbessert. Dabei kann diese nur verbessert werden, wenn sich die Position nicht gleichzeitig verschlechtert. Durch das
frühe Ansteuern der Position lassen sich die im Vektor hinten stehenden Werte zur
Feinkorrektur gut nutzen.
165
13 Einparken mit Anhänger
Abbildung 13.2.: Endposition mit Fitness 50 bei Bewertung 3
Es kann jedoch vorkommen, dass die Ausrichtung nicht mehr verbessert werden
kann ohne dabei die Position zu verschlechtern. In diesem Fall ist kaum mehr eine
Verbesserung möglich.
Daher wurde eine weitere Bewertung untersucht. Bei dieser Bewertuing wird die
Y-Abweichung ausser acht gelassen. Die Anteile der X-Abweichung, so wie der Verdrehung des Fahrzeugs und des Anhaengers werden härter Bestraft. Besonders der
Unterschied zwischen kleinen Verdrehungen und Grossen hat hier deutlich mehr
Gewicht als zuvor.
BewertungX
BewertungY
BewertungR
BewertungA
=
=
=
=
Pow( AbweichungX, 2)*10
0
Pow( AbweichungR*180, 2)*2
Pow( AbweichungR*180, 2)
Für diese Bewertung wurde der Konvergenzwert auf 20 festgelegt. Wie in Abbildung 13.3 zu erkennen sind selbst Ergebnisse mit Fitness 10 hier im Grunde noch
akzeptabel.
166
13.5 Weitere Bewertungen
Abbildung 13.3.: Endposition mit Fitness 10 bzw. 20 bei Bewertung 4
Populationsgröße
Generationen
1000
32.7
2000
30.6
20000
5.5
Tabelle 13.4.: Testergebnisse bei Bewertung 4
Mit 5 von 10 gefundenen Lösungen bei 1000 Individuen scheint diese Bewertung
die Konvergenz besser zu unterstützen. Auch die durchschnittliche Generationenanzahl liegt besser als bei den anderen Bewertungen. Mit einer Populationsgröße
von 2000 erreichen weiterhin 5 von 10 Durchläufen das gesetzte Ziel. Die erhöhte
Konvergenzgeschwindigkeit und die im Schnitt besseren Fitnesswerte nach 50 Generationen lassen bessere Ergebnisse bei größeren Populationszahlen erwarten.
Um dies zu bestätigen, wurden daher zusätzlich 10 Durchgänge mit 20000 Individuen pro Generation durchgeführt. Alle Durchgänge erreichen hier das geforderte
Ergebnis. Trotz der mit 5.5 Generationen sehr schnellen Konvergenz ist der Zeitaufwand erheblich. Auf dem Testsystem wurde eine Generation in 4 bis 5 Minuten
bearbeitet. Bis zur Lösungsfindung eines Durchgangs muss man daher etwa mit einer halben Stunde rechnen.
Es ist zu erwarten, dass die in den bisherigen Tests festgestellten Beschleunigungen
167
13 Einparken mit Anhänger
auch für dieses Problem gelten.
Um dies zu zeigen, wird die Messung nun auch mit 5000 Individuen durchgeführt.
Diese Messung wird anschließend mit Eliten und 10% Mutations-Wahrscheinlichkeit
wiederholt.
Populationszahl
Standard
Eliten
10 % Mutationsw.
5000
18
20.7
9.5
Tabelle 13.5.: Weitere Testergebnisse bei Bewertung 4
Mit 5000 Individuen konnten 8 von 10 Lösungen gefunden werden. Mit einer durchschnittlichen Konvergenzzeit von 18 Generationen kann dieses Ergebnis als sehr gut
betrachtet werden.
Bei Mitnahme von Eliten steigt die Konvergenzzeit auf 20.7 Generationen. Die
Konvergenz-Wahrscheinlichkeit bleibt unverändert. Es ist daher anzunehmen, dass
Eliten zumindest keinen Vorteil für ein so komplexes Problem erreichen. Durch die
Erhöhung der Mutations-Wahrscheinlichkeit auf 10% konnte das Erreichen einer Lösung für jeden Durchgang erwirkt werden. Außerdem konnte die durchschnittliche
Zeit auf 9.5 gesteigert werden. Was die Bedeutung der Mutations-Wahrscheinlichkeit
erneut verdeutlicht.
Da die Wahrscheinlichkeit, einen guten Ansatz zu finden für alle Bewertungen gleich
gering ist, lässt sich das Ergebnis nur dadurch verbessern, dass eine Möglichkeit gefunden wird, frühzeitig zu erkennen, welcher Ansatz die besten Aussichten hat, eine
Lösung zu finden. Die zuletzt getestete Bewertung scheint dieses Problem am Besten
zu behandeln. Durch den großen Zeitaufwand war es nicht möglich, alle Bewertungen auf ihr Verhalten bei großen Populationsgrößen hin zu untersuchen.
168
14. Populationsmodelle
Die oben beschriebenen Versuche wurden mit jeweils einer Insel durchgeführt. Das
heißt, für jeden Durchlauf wurde eine Ausgangspopulation erzeugt und diese bis zum
Abbruchkriterium bearbeitet. Diese Konfiguration wird im Folgenden als Standardmodell bezeichnet. Es ist das einfachste und meistverwendete Populationsmodell bei
genetischen Verfahren.
Der EAServer unterstützt neben dem Standardmodell auch das Inselmodell und das
Netzwerkmodell, deren Eigenschaften und Auswirkungen für die Evolution im Folgenden erläutert werden.
14.1. Einparken ohne Anhänger
14.1.1. Inselmodell
Das Inselmodell generiert eine festgelegte Zahl verschiedener Ausgangspopulationen,
die im Verlauf der Evolution nebenläufig bearbeitet werden.
Dieses Modell ist, wie der Name schon vermuten lässt, von der Artenentwicklung
auf Inseln im Meer inspiriert. Die Isolation der Inseln ist bei dem genetischen Algorithmus jedoch noch konsequenter. Die Populationen werden vollständig unabhängig
voneinander erzeugt und bearbeitet. Die Individuen der Inseln beeinflussen sich bei
diesem Modell nicht.
Erreicht eine Insel ein Abbruchkriterium, wird die Evolution aller Inseln beendet
und das beste Ergebnis als Lösung präsentiert. Im Gegensatz zum wiederholten
Ausführen der Evolution ist es also nicht notwendig, dass jede Ausgangspopulation
den Konvergenzwert erreicht. Außerdem ist der Zeitaufwand des Ausführens eines
Durchlaufs mit mehreren Inseln durch den Abbruch bei Konvergenz einer Insel geringer als beim hintereinander ausführen der gleichen Anzahl einzelner Populationen.
Offensichtlich dürfte das Inselmodell dann Vorteile bringen, wenn die zur Konver-
169
14 Populationsmodelle
genz benötigte Zeit stark schwankt. Auch wenn ein Problem schwer lösbar ist und
oftmals kein Ergebnis erzielt werden kann, ist eine Beschleunigung durch das Inselmodell zu erwarten.
Andererseits dürfte sich bei Problemen mit geringen Konvergenzzeiten die Verwendung des Inselmodells negativ auf die Laufzeit des Algorithmus auswirken. In diesen
Fällen wird normalerweise von fast jeder Ausgangspopulation aus ein optimales Ergebnis erreicht. Daher ist kein mehrmaliges Ausführen notwendig und es wird daher
auch keinen Vorteil bringen, das Inselmodell zu verwenden.
Der folgende Versuchslauf soll diese Überlegungen bestätigen.
In allen Fällen werden diese Standardkonfigurationen verwendet, sofern für einen
bestimmten Versuchsaufbau nichts anderes beschrieben wird:
Populationsmodel
Populationszahl
Problem
Genlänge
UpperA
Crossover
CO Probability
Mutation
M Probability
Termination
Generation
Convergence value
Selection
Mating
Replacement
siehe Versuchsbeschreibung
500
Vehicle
50/65
3
One Point
100%
Equal
4%
Convergence & Generation
Maximum 100
1000
Roulette wheel
Random
Generational
Tabelle 14.1.: Standardkonfiguration
Als Problem wird zunächst das Einparken ohne Anhänger gewählt. Hier konnte eine
Bewertung gefunden werden, die mit 200 Individuen je Generation recht sicher konvergiert. Es ist also davon auszugehen, dass das Inselmodell einen geringen Vorteil
bringt. Es ist zu erwarten, dass sich sowohl Konvergenzsicherheit wie auch Konvergenzgeschwindigkeit verbessern. Ob sich der Mehraufwand letztlich auszahlt, wird
170
14.1 Einparken ohne Anhänger
sich mit diesem Test zeigen.
Der Versuch läuft wie folgt ab:
Für die selbe Situation wird zunächst mit einer Ausgangspopulation die Evolution
durchgeführt. Die zur Konvergenz benötigte Zeit in Generationen ist hier der relevante Wert. Dies wird 10 mal wiederholt und ergibt eine durchschnittliche Konvergenzgeschwindigkeit. Das 10-malige Wiederholen des Tests ermöglicht nur näherungsweise Aussagen über statistischen Ergebnisse. Besonders im Bereich der unsicheren
Konvergenz ergeben sich starke Schwankungen, die Aussagen über durchschnittliche
Werte und zu erwartende Ergebnisse erschweren. Die im Folgenden beschriebenen
Ergebnisse und Schlussfolgerungen beruhen auf den Versuchsläufen.
100
51
28
erzielte Zeiten
9 14 100 11
25
16
100
Durchschnitt
70.8
Tabelle 14.2.: Zeiten mit Standardmodell
Es ist zu beachten, dass diese Zeiten stark von der Ausgangssituation abhängen und
keine absoluten Zeiten für das Lösen des Problems sind. Die Durchläufe mit 100
Generationen sind nicht konvergent. Gerade diese Fälle werden bei Verwendung des
Inselmodells weitgehend wegfallen. Die Abweichung von oben durchgeführten Läufen
mit dieser Konfiguration sind, wie bereit erläutert, bedingt durch die sehr hohe
Schwankung der einzelnen Zeiten und die geringe Anzahl Messungen. In der Messung
„Einparken ohne Anhänger“ wurde bei 200 Individuen eine Durchschnittszeit von
41.15 erreicht.
Im Folgenden werden die durchschnittlichen Laufzeiten von Versuchsläufen mit dem
Inselmodell ermittelt. Es werden 2, 5 und 10 Inseln verwendet.
Um die tatsächliche Laufzeit in Generationen zu bestimmen wird der ermittelte
Wert mit der Anzahl der Inseln multipliziert:
Inseln
2
5
10
26
4
9
13
9
11
8
11
4
erzielte
18 15
14 13
9
8
Zeiten
13 11
12 14
7
9
78
10
9
74
6
15
14
12
10
Durchschnitt
27
10.5
9.1
tats. Zeit
54
52.5
91
Tabelle 14.3.: Zeiten mit Inselmodell (ohne Anhänger)
Bereits die Verwendung von 2 Inseln beseitigt die nicht konvergierenden Läufe und
171
14 Populationsmodelle
erhöht damit die Konvergenz-Wahrscheinlichkeit. Da es sich beim Inselmodell um
das Ausführen unabhängiger Tests handelt, lässt sich dies durch Wahrscheinlichkeitsrechnung vorhersagen. Da eine Insel zu 30% nicht konvergiert, beträgt die Wahrscheinlichkeit, dass zwei Inseln kein Ergebnis erbringen demnach 9%. Der bereits bei
„Einparken ohne Anhänger“ durchgeführte Versuch ergab 20% nicht konvergierender
Läufe. Nimmt man diesen Wert an, ergibt sich für zwei Inseln eine Wahrscheinlichkeit von 4%. Da tatsächlich kein Lauf ohne Lösung geblieben ist, lässt sich dieser
Wert nicht nachprüfen.
Die erreichten Geschwindigkeiten schwanken recht stark. Insgesamt scheint die Verwendung des Inselmodells sich auszuzahlen.
Wie zu erwarten, ist die Konvergenzgeschwindigkeit hoch genug um keine deutliche
Verbesserung durch mehr Inseln zu erfahren. Die gemessenen Zeiten liegen bei 5
Inseln dichter beieinander. Mit 0.03 - 0.24 % rechnerischer Erfolglosigkeit sind lang
verzögerte Ergebnisse oder gar das Ausbleiben der Konvergenz nicht zu beobachten.
Dies lässt sich durch die starken Schwankungen der ursprünglichen Messung erklären. Zwei der Durchläufe waren mit 9 bzw. 11 Generationen recht schnell. Daher ist
es zu erwarten, dass wenigstens eine von 5 Inseln eine ähnliche Geschwindigkeit erreicht. Durch die größere Inselzahl ist die tatsächliche Geschwindigkeit nicht besser
als mit 2 Inseln. Bei weiterer Steigerung der Inselzahl ist eher mit einer Verlangsamung der Laufzeit zu rechnen.
Bei 10 Inseln ergeben sich sehr gute Konvergenzzeiten, in den meisten Fällen von
weniger als 10 Generationen. Die Leistung ist damit besser, als zunächst zu erwarten gewesen wäre. Da auch Populationen mitberechnet werden müssen, die nicht
zum Erreichen des Zieles benötigt werden, ist der tatsächliche Rechenaufwand erwartungsgemäß deutlich größer als mit nur 5 oder 2 Inseln.
Insgesamt kann man feststellen, dass sich die Verwendung des Inselmodells durchaus auszahlen kann. Die Verwendung einer größeren Anzahl Inseln erhöht die Wahrscheinlichkeit, eine optimale Lösung zu erhalten. Ab einer bestimmten Anzahl nimmt
der Nutzen allerdings durch den höheren Zeitaufwand wieder ab. Für dieses Problem
liegt die optimale Inselzahl bei drei bis vier Inseln.
Der Vorteil des Inselmodells liegt in der Nutzung des besten Laufs aus einer Reihe
von Durchläufen. Die Konvergenzgeschwindigkeit lässt sich mit Hilfe von verschiedenen Parametern steigern. Es hat sich für dieses Problem eine Annäherung an 6 bis
172
14.1 Einparken ohne Anhänger
7 Generationen als schnellst möglich herausgestellt. Bei z.B. niedrigen Populationszahlen sind solche Geschwindigkeiten selten. Sie lassen sich aber durch Verwendung
des Inselmodells empirisch finden. Das erhöhte Vorkommen solcher Durchgänge bei
Erhöhung der Populationszahl verringert den Vorteil des Inselmodells, so dass anzunehmen ist, dass die Steigerung der Leistung durch Nutzung mehrerer Inseln vermutlich geringer ausfällt.
Dies wird später noch genauer betrachtet.
14.1.2. Netzwerkmodell
Das Netzwerkmodell ist ein erweitertes Inselmodell, bei dem der Austausch geringer
Mengen Erbgutes unter den Inseln möglich ist. Dies ist eine Umsetzung von Beobachtungen über die Artenentwicklung größerer Inselgruppen. Es entwickeln sich
somit weitgehend unabhängige Populationen, die durch Einwanderer eine Konkurrenz aber auch eine Auffrischung der genetischen Vielfalt erfahren.
Das Netzwerkmodell hat einen Hard-codierten Austauschanteil von 10%.
Auch beim Netzwerkmodell gilt das Problem als gelöst, wenn es von einer Population gelöst wurde.
Der gegenseitige Einfluss soll verhindern dass eine der Populationen auf einem Fitnesswert stagniert. Erreicht eine Population sehr gute Werte, so ist zu erwarten, dass
die anderen Knoten dieses Erbgut, möglicherweise in abgewandelter Form, übernehmen. So kann sich ein gutes Ergebnis schnell in der eigenen Population durchsetzen,
in den Anderen bleibt die Varianz hoch, was für eine weitere Verbesserung sorgen
kann.
Eine mögliche Schwäche gegenüber dem Inselmodell ist, dass sich Individuen durchsetzen können, wenn sie genügend hohe Werte erreichen. Da aber ein hoher Wert
keine Garantie für letztlich eine Konvergenz ist, könnte dies die Konvergenz der
Population behindern. Da sich die Gene auch auf die anderen Inseln übertragen,
könnte die Evolution zum Erliegen kommen.
Die Versuchskonfiguration stimmt weitestgehend mit der der Versuchsreihe zum Inselmodell überein.
Die Durchschnittszeit ohne ein erweitertes Modell wird aus der Versuchsreihe zum
Inselmodell übernommen.
173
14 Populationsmodelle
Knoten
2
5
10
13
5
9
19
10
8
8
13
8
erzielte
11 11
6
8
7 11
Zeiten
10 13
10 12
9 10
99
11
7
12
13
8
13
11
8
Durchschnitt
20.9
9.9
8.5
tats. Zeit
41.8
49.5
85
Tabelle 14.4.: Zeiten mit Netzwerkmodell (ohne Anhänger)
Bei 2 Knoten werden sowohl die erwarteten Verbesserungen als auch die befürchteten Probleme bestätigt.
Die Konvergenzgeschwindigkeit ist im Durchschnitt besser als mit dem Standardmodell. Sie ist sogar noch besser als mit dem Inselmodell.
Der eine Ausreißer mit 99 Generationen bestätigt die theoretische Schwäche des
Netzwerkmodells und macht es schwer eine zur Konvergenz benötigte Zeit abzuschätzen. Die Leistung des Netzwerkmodells entspringt der größeren Ausgangsvielfalt, die, ähnlich wie bei größeren Populationszahlen, gute Ansätze mit sich bringen
kann. Nach einigen Generationen hauptsächlich lokaler Evolution haben sich für jeden Knoten favorisierte Ansätze durchgesetzt. Ab dann wird eine Vermischung der
Ansätze immer wahrscheinlicher. Aus den entwickelten Ansätzen wird sich nun der
beste durchsetzen und die anderen langsam verdrängen. Im Gegensatz zur reinen
Erhöhung der Populationszahl wirkt sich die Vielfalt und damit die geringere Verarmung anders aus. In jedem Knoten ist die Vielfalt gering und die Verarmung somit
recht schnell. Über die Knotengrenzen hinaus bleibt die Vielfalt länger bestehen, so
dass auch spätere Entwicklung möglich ist.
Der Testlauf mit 5 Knoten ergibt gute Werte, die alle recht nah bei einander liegen.
Die Schwäche des Netzwerkmodells scheint sich hier nicht mehr auszuwirken. Die
tatsächliche Durchschnittszeit ist allerdings höher als mit 2 Knoten. Sie liegt im selben Bereich wie beim Inselmodell mit 5 Inseln. Die optimale Knotenzahl für dieses
Modell liegt vermutlich bei 2 bis 3 Knoten.
Bei 10 Knoten ergibt sich das selbe Bild wie beim Inselmodell mit 10 Inseln. Die
Zeiten sind im Grunde sehr gut, durch die Verwaltung von 10 Populationen, die hier
alle von Bedeutung sind, ist die tatsächliche Laufzeit aber zu hoch um mit anderen
Konfigurationen mithalten zu können.
Insgesamt scheint sich die Verwendung des Netzwerkmodells durchaus zu lohnen.
Besonders die deutlichen Verbesserungen die schon durch 2 Knoten erreicht werden
174
14.2 Einparken mit Anhänger
können, überzeugen.
Gerade beim Netzwerkmodell könnte man annehmen, dass die Verbesserung der Geschwindigkeit hauptsächlich von der erhöhten Anzahl Individuen herrührt.
Daher wird zum Vergleich eine Messreihe mit 400, 1000 und 2000 Individuen durchgeführt.
Pop.gr.
400
1000
2000
11
9
6
12
8
8
7
7
7
erzielte Zeiten
9 10 12 9 13
7
5 10 8
5
7
8
4 7
7
31
6
7
12
9
7
Durchschnitt
12.6
7.4
6.8
Tabelle 14.5.: Zeiten bei größeren Populationszahlen (ohne Anhänger)
Die Verwendung von 400 Individuen ist sowohl gegen das Inselmodell mit 2 Inseln
als auch gegenüber dem Netzwerkmodell mit 2 Knoten zu bevorzugen.
Die Verwendung von 1000 Individuen ergibt ebenfalls bessere Zeiten als die Verwendung von 5 Inseln bzw. 5 Knoten. Auch mit 2000 Individuen werden bessere
Ergebnisse erzielt als mit 10 Inseln oder 10 Knoten.
Der Grund für die Überlegenheit der größeren Individuenzahl ist in der größeren
genetischen Vielfalt zu suchen. Es ist anzunehmen, dass dieser Vorteil bei dem recht
einfachen Problem des Einparkens ohne Anhänger besonders stark ausfällt. Es wird
sich im Rahmen der Versuchsreihe zum Einparken mit Anhänger zeigen, ob diese
These bestätigt werden kann.
14.2. Einparken mit Anhänger
Das Problem des Einparkens mit Anhänger ist wesentlich komplexer als das Einparken ohne Anhänger. Obwohl die Toleranz der Optimallösung größer ist, wird
diese selten erreicht. Um vergleichbare Ergebnisse zu erhalten, wird nochmals eine Gesamttoleranz angewandt. Dies erfolgt, indem als Abbruchbedingung nicht die
Konvergenz gegen 1000 eingestellt wird, sondern gegen 20. Die Evolution endet also,
wenn die Simulation eine Bewertung von 50 liefert. Bereits bei einer Bewertung von
100 kann das Fahrzeug als eingeparkt angesehen werden.
175
14 Populationsmodelle
Durch diese Toleranz soll erreicht werden, dass die Evolution mit einem guten Ergebnis vor Erreichen der Generationenhöchstzahl beendet werden kann. So werden
verschiedene Konfigurationen besser vergleichbar. Da der Konvergenzaufwand wesentlich größer ist, werden verwertbare Ergebnisse nur mit größeren Populationszahlen erbracht. Daher wird die Populationsgröße für die Tests ohne bzw. mit erweitertem Modell auf 500 gesetzt. Dadurch steigert sich der Zeitaufwand. Dies soll durch
eine geringere Höchstlaufzeit ausgeglichen werden. Dabei wird in Kauf genommen,
dass die Evolution unterbrochen wird, obwohl möglicherweise bessere Ergebnisse zu
erzielen gewesen wären.
Die restlichen Einstellungen entsprechen den oben gewählten.
Das Einparken mit Anhänger ist stärker von der Ausgangspopulation abhängig, so
dass zu erwarten ist, dass sich die Konvergenzgeschwindigkeit durch Verwendung
des Insel- oder Netzwerkmodells deutlich verbessert.
Zunächst wird auch für diesen Test die durchschnittliche Konvergenzzeit ohne erweitertes Modell bestimmt:
11
50
22
erzielte Zeiten
50 50 17 15
50
50
50
Durchschnitt
36.5
Tabelle 14.6.: Zeiten mit Standardmodell
Der mit 60% sehr hohe Anteil von Durchgängen, die nicht innerhalb der gegebenen Zeit das geforderte Ergebnis erbringen konnten, war zu erwarten. Das Problem
des Einparkens mit Anhänger ist so komplex, dass die Anfangspopulation, vor allem aber Entwicklungen während der ersten paar Generationswechsel den Verlauf
entscheidend festlegen. Konnte die Grundlage für ein sehr gutes Einparken nicht
innerhalb der ersten Generationen gelegt werden, wird das Ergebnis in den weiteren Generationen nur noch marginal verbessert. Entscheidende Änderungen können
nicht mehr erwartet werden. Die verbleibenden vier Durchgänge legen gute Zeiten
vor. Betrachtet man diese Werte, sind deutliche Verbesserungen durch die Verwendung eines erweiterten Modells zu erwarten.
14.2.1. Inselmodell
Im Folgenden werden die Versuche mit der selben Situation unter verwendung des
Inselmodells durchgeführt. Es werden dabei 2, 5 und 10 Inseln eingestellt und auf
176
14.2 Einparken mit Anhänger
ihren Nutzen hin untersucht.
Inseln
2
5
10
50
50
5
10
12
5
9
7
7
erzielte
50 50
46
7
3 11
Zeiten
5 50
14 10
10 13
19
5
7
4
9
6
22
8
10
Durchschnitt
26.9
16.8
7.7
tats. Zeit
53.8
84
77
Tabelle 14.7.: Zeiten mit Inselmodell (mit Anhänger)
Die besseren Durchschnittswerte, die sich bei 2 Inseln gegenüber dem Standardmodell ergeben, werden dadurch erreicht, dass ein gewisser Anteil derjenigen Ursprungspopulationen, die kein Ergebnis hervorbringen, durch eine andere die eine
Lösung erbringt, verdeckt wird. Da ohne Inselmodell 60% keine Lösung erzielen,
liegt der erwartete Wert der nicht Konvergierenden bei 36%.
Der tatsächliche Zeitaufwand durch Verwendung des Inselmodells steigt. Die reduzierte Zahl der ergebnislosen Durchläufe wiegt in diesem Fall allerdings schwerer, so
dass hier dennoch von einem Gewinn gesprochen werden kann. Die erreichten Zeiten
zeigen, dass noch bessere Ergebnisse erwartet werden können. Eine Vergrößerung der
Inselzahl wird sich mit Sicherheit lohnen.
Bei 5 Inseln liegt die erwartete Zahl der nicht konvergierenden Durchläufe bei etwa
8%.
Wenn in einem Durchlauf wenigstens eine Population zu finden ist, die ein gutes
Ergebnis erwarten lässt, konvergiert er im Allgemeinen recht rasch. Die Anzahl der
Generationen, die notwendig sind, um aus einem guten Ansatz ein gutes Ergebnis zu
machen, ist kaum höher als beim Einparken ohne Anhänger. Einzig das Finden eines
guten Ansatzes ist wesentlich schwerer. Die tatsächliche Laufzeit ist im Schnitt mehr
als doppelt so hoch wie ohne erweitertes Modell. Dieser Wert ist durch die hohe Anzahl der nicht konvergierten Durchgänge jedoch nur eingeschränkt aussagekräftig,
da für diese ein Höchstwert von 50 gegeben ist.
Soll mit jedem Durchgang ein Ergebnis erbracht werden, lohnt sich der Mehraufwand aber auf jeden Fall.
Bei 10 Inseln liegt die theoretische Quote nicht konvergierender Durchläufe noch bei
ca. 0.5%, so dass man davon ausgehen kann, dass jeder gestartete Durchgang auch
177
14 Populationsmodelle
ein gutes Ergebnis erzielt.
Die Zahl der benötigten Generationen ist hier so gering, dass sich die Verwendung
von 10 Inseln durchaus lohnen kann, da der tatsächliche Zeitaufwand mit 77 unter
dem von 5 Inseln liegt und durch die sehr hohe Konvergenz-Wahrscheinlichkeit der
Verwendung von 2 Inseln vorzuziehen ist.
Der Vorteil des Inselmodells zeigt sich immer deutlicher, je komplexer das Problem
ist.
Erhöht man die Komplexität dieses Problems, indem man den Konvergenzwert auf
100 setzt, ergeben sich bei 10 Inseln die in Tabelle 14.8 angegebenen Zeiten.
9
50
43
erzielte Zeiten
15 50 25 46
6
11
24
Durchschnitt
36.9
Tabelle 14.8.: Zeiten mit 10 Inseln und Konvergenzwert 100
Daraus lässt sich ersehen, wie schwer dieser Fitnesswert zu erreichen ist. Mit weniger
Inseln würden sich kaum noch brauchbare Lösungen ergeben.
Eine weitere Steigerung würde auch die weitere Erhöhung des Konvergenzwertes ermöglichen. Da dadurch aber die benötigte Zeit immer weiter zunimmt, sollte man
auf dieses Mittel nur dann zurückgreifen, wenn man bei einem Durchlauf unbedingt
eine Lösung erreichen will.
14.2.2. Netzwerkmodell
Unter Verwendung des Netzwerkmodells sollte sich die Anzahl der nicht konvergierenden Durchläufe reduzieren. Es ist davon auszugehen, dass auch die tatsächliche
Zeit verbessert werden kann.
Knoten
2
5
10
15
10
5
50
26
9
50
6
7
erzielte Zeiten
5 7 17 12
7 2 50 11
9 9
9 13
15
6
5
50
8
2
13
10
15
Durchschnitt
23.4
12.6
8.3
Tabelle 14.9.: Zeiten mit Netzwerkmodell (mit Anhänger)
178
tats. Zeit
26.8
63
83
14.2 Einparken mit Anhänger
Bereits bei 2 Knoten zeigt sich eine deutliche Verbesserung der Konvergenzeigenschaften. Die Zahl der erfolglosen Durchgänge nimmt ab. Gleichzeitig ist auch bei
den erfolgreichen Durchgängen eine Verbesserung zu beobachten. Nach diesem ersten Ergebnis scheint das Netzwerkmodell auch für dieses Problem dem Inselmodell
überlegen zu sein. Es ist zu erwarten, dass sich diese Ergebnisse durch die Erhöhung
der Knotenzahl weiter verbessern.
Die Ergebnisse liegen bei 5 Knoten in den meisten Fällen gut. Es kann mit dieser
Konfiguration zwar noch zu nicht konvergierenden Durchgängen kommen, diese sind
jedoch eher die Ausnahme. Sollte sich dieses Problem mit 10 Knoten beseitigen lassen, ist eine Durchschnittszeit von 8-10 durchaus möglich.
Bei dieser Einstellung ist weder Netzwerkmodell noch Inselmodell deutlich überlegen, so dass keine Empfehlung für eines der beiden Modelle abgegeben werden kann.
Auch beim Netzwerkmodell gilt jedoch, dass sich durch die Reduzierung der ergebnislosen Tests der Mehraufwand lohnt.
Mit 10 Knoten ergeben sich geringfügig schlechtere Werte als mit der gleichen Anzahl
im Inselmodell. Jedoch kann auch nach Betrachtung dieser Ergebnisse kein eindeutiges Urteil darüber gefällt werden, welches der beiden Modelle zu bevorzugen ist.
Vergleich mit größeren Populationszahlen:
Pop.gr.
1000
2500
5000
8
9
6
50
25
50
12
9
21
erzielte Zeiten
50 14 50 50
50 50 11
7
50 12
6
8
50
10
6
8
9
11
50
6
7
Durchschnitt
34.2
18.6
17.7
Tabelle 14.10.: Zeiten bei größeren Populationszahlen(mit Anhänger)
Im Vergleich mit den jeweiligen Ergebnissen aus den obrigen Tests zeigt sich, dass
die Nutzung eines erweiterten Models der Erhöung der Populationszahl hier vorzuziehen ist. Selbst mit 5000 Individuen je Generation kamen immernoch erfolglose
Durchgänge vor, die bei 10 Inseln bzw. 10 Knoten ausblieben.
Es lässt sich daher feststellen, dass der Einsatz erweiteter Populationsmodelle bei
sehr komplexen Problemen durchaus ratsam ist.
179
15. Ausblick
15.1. Parallelisierung eines genetischen
Algorithmus
Diverse Erweiterungen der EALib- bzw. EAServer -Bibliothek ermöglichen eine Einführung von Parallelität (vgl. Tabelle 15.1) in die evolutionären/genetischen Algorithmen.
Die Erzeugung der Ausgangspopulation lässt sich dadurch parallelisieren, dass jedes
Individuum für sich und unabhängig von den anderen Individuen der Population erzeugt wird. In diesem Fall gibt es keine Einschränkung der Parallelisierbarkeit. Die
Berechnung der Fitness eines konkreten Individuums stellt ebenfalls kein Problem
dar. Jedes Individuum kann unabhängig von den anderen auf seine Tauglichkeit und
Güte geprüft werden. Somit ist auch dieser Schritt parallelisierbar.
Die Parallelisierbarkeit der Errechnung oder Überprüfung der Abbruchbedingung
der genetischen Algorithmen hängt von den Abbruchkriterien ab. Ist die Abbruchbedingung an die Anzahl der Generationen oder die verbrauchte Rechenzeit geknüpft,
lässt sie sich in der Regel sehr leicht ermitteln und muss nicht parallelisiert werden.
Die übliche Abbruchbedingung bei den genetischen Algorithmen ist allerdings eine
Funktion der Fitness eines oder einiger Individuen. Es wird dann der Algorithmus
abgebrochen, wenn das beste Individuum eine bestimmte Güte erreicht hat oder
wenn sich die Güte des oder der besten Individuen über eine längere Zeit nicht oder
nicht mehr wesentlich verändert. In beiden Fällen setzt dies die Kenntnis der Fitness
der besten Individuen und damit die Kenntnis der Fitness aller Individuen voraus.
Die Berechnung oder Prüfung der Erfüllung der Abbruchbedingung lässt sich somit
nur zentral ermitteln und ist nicht parallelisierbar. Die Abbruchprüfung ist eine zentrale Steuerungsfunktion der Algorithmen und deren Flaschenhals.
Ähnlich wie die Abbruchbedingung kann auch die Auswahl der zu rekombinierenden Individuen (Selektion) nicht parallelisiert werden. Dies ist insbesondere der Fall,
181
15 Ausblick
wenn die Selektion der Individuen proportional zur Fitness der Individuen (Roulette
Wheel) vorgenommen werden soll oder in einer anderen Weise von der Fitness der
Gesamtpopulation abhängt.
Der Crossing-over Prozess hingegen ist völlig unabhängig vom Crossing-over anderer, unbeteiligter Individuen und kann demnach parallel in der gesamten Population
ablaufen. Dies kann gegenüber einem seriellen Algorithmus einen enormen Geschwindigkeitsvorteil mit sich bringen. Der potentielle Geschwindigkeitsvorteil ist hierbei
umso größer, je komplizierter und damit rechenintensiver der Crossing-over Mechanismus ist.
Die Mutationen sind ebenfalls parallelisierbar, da sie nur lokal auf die einzelnen
Individuen wirken. Nach der Rekombination der Individuen besteht bei einer fiEvolution
Prozess
Ebene von Individuen
Erzeugung Ausgangspopulation
Berechnung Fitness
Prüfung Abbruchbedingung
Selektion
Crossing-over
Mutation
Ersetzung
Ebene von Populationen
Parallelisierbar
√
√
Insel-Modell
Netzwerk-Modell
Kommunen-Modell
√
√
√
√
√
Tabelle 15.1.: Parallelisierung der evolutionären Prozesse
xen Populationsgröße ein Überschuss an Individuen. Aus der gesamten Population
müssen nun die besten nach dem Selektionskriterium ausgesondert werden, um die
Populationsgröße konstant zu halten. Dies erfordert somit die Kenntnis der Fitness
aller Individuen und stellt einen zentralen Steuerungsmechanismus dar, der nicht
parallelisierbar ist. Eine gewisse Parallelisierung der Ersetzung ist dennoch möglich,
wenn die Populationen in Hierarchien von Subpopulationen aufgeteilt wären und in
diesen lokal selektiert würden. Aber in diesem Fall hätte man im eigentlichen Sinn
bereits eine Evolution von Population, wie Kapitel 5 beschreibt und welche alle
hochgradig parallelisierbar sind. Ist hingegen die Populationsgröße nicht konstant,
so entfällt der Selektionsschritt teilweise. Es ist dann möglich, die Populationen über
182
15.2 Erweiterungen der Server-Software
mehrere Generationen hinweg unbeschränkt wachsen zu lassen und nur gelegentlich
nach jeweils n Generationen zu selektieren. Ganz auslassen könnte man die Selektion bzw. Ersetzung jedoch nicht, da ansonsten der Evolutionsprozess kombinatorisch
durch die ständige Vermehrung der Nachkommen explodiert.
Diese hier beschriebene Parallelisierung könnte mittels Threads realisiert werden.
Aber da evolutonäre Algorithmen einen gewissen Aufwand an Rechenleistung bedingen, wäre es besser eine solche Parallelisierung nur dann vorzehmen, wenn ein
Multiprozessorsystem zur Verfügung steht. Um die in den Bibliotheken – EALib
und EAServer – vorhandenen seriellen Vorgänge zu parallelisieren wäre eine entsprechende Erweiterung zu konzipieren und einzubauen.
15.2. Erweiterungen der Server-Software
Ein weiterer Ausbau der Software wäre die Teilung des Servers. Der erste Teil
stellt im wahrsten Sinne des Wortes den eigentlich Server dar, welcher die EALibBibliothek beinhaltet und durch ihr genetische Algorithmen verschiedenen Klienten
zur Verfügung stellt. Diese Klienten repräsentieren den zweiten Teil des bisherigen
Servers. Sie besitzen die Benutzerschnittstelle und sind selbst wiederum Server für
einen Klienten, der z.B. eine Simulation eines Fahrzeugs bereitstellt. Vorteil dieses verteilten Systems wäre es einen genetischen Server zu besitzen der z.B. über
TCP mehreren Klienten simultan genetische Algorithmen anbieten kann, so dass
eine gleichzeitige Bearbeitung unterschiedlicher Problemfelder ermöglicht wird. In
diesem Bereich könnte ebenfalls die oben beschriebene Parallelisierung stattfinden,
indem jeder verbundene Klient sein eigenes Multiprozessorsystem zugewiesen bekommt.
Neben diversen Parallelisierungen und Verteilungen des Systems stellt die Erweiterung des Algorithmus, um weitere Strategien einen wichtigen Gesichtspunkt dar.
Aufgrund des im Kaptitel 6 beschriebenen Konzepts der einzelnen Pakete ist dies
ohne weiteres möglich. So können neben Mutations- und Crossing-over auch Operatoren wie Inversion1 in den Algorithmus eingebracht werden. Auch würde eine
geringfügige Anpassung der Schnittstelle EAGenom die Einführung komplexerer Vermehrungsalgorithmen erlauben, so dass z.B. Geschlechter simuliert werden könnten.
Auch der Einbau von Dominanz und Diploidie sind theoretisch denkbar, jedoch da
1
wichtiger Operator für Pfadplanungsprobleme
183
15 Ausblick
sowohl keine Theorie über den Einbau einer Dominanzfunktion auch als auch keine experimentellen Daten über ihren Nutzen existieren, wurde im Rahmen dieser
Diplomarbeit darauf verzichtet.
15.3. Codierung Car
Die alternative Codierung Car basiert auf einem Arithmetischen Baum. Der jeweilige Lenkeinschlag wird anhand einiger Parameter berechnet. Somit handelt es sich
bei dieser Codierung um eine sehr dynamische Variante, die beliebige Zeitvorgaben
und Situationsvarianten erfüllen kann. Die Nutzung eines Baumes zur Codierung ermöglicht es jedes mathematische Problem wenigstens näherungsweise zu Lösen ohne
das eine Änderung der Codierung notwendig ist. Innerhalb des nahezu unbegrenzten Suchraumes existieren auch Lösungen für weitaus komplexere Probleme, wie
etwa das Einparken mit verschiedenen Ausgangssituationen. Dies würde die Wiederverwertbarkeit sowie die praktische Nutzbarkeit gefundener Lösungen deutlich
erhöhen.
Der Baum muss jedoch aufwendig konstruiert, als String codiert und übertragen
werden. Bei der Simulation angekommen muss er wieder aufgebaut werden und
wird dann je nach Problem 50 mal und öfter durchgerechnet. Der Zeitaufwand hierfür hängt von der Größe des Baumes ab. Vor allem zu späteren Zeitpunkten eines
Durchlaufs erreichen die Bäume große Dimensionen. Teilweise erreichen sie 100 und
mehr Knoten, was dazu führt, dass die Individuen und somit die Generationen immer
mehr Zeit benötigen. Die Laufzeit der Problemlösung ist daher schwer abschätzbar.
Auch der Bedarf an anderen Ressourcen wie etwa Speicher nimmt mit der Zeit zu.
Die Codierung Car wurde in der EALib implementiert und ihre Verwendung in der
Simulation ermöglicht. Jedoch wurde, nach einigen Tests, entschieden, diese Codierung nicht weiter zu untersuchen. Grundsätzlich können mit dieser Codierung bessere Ergebnisse, auch zu komplexeren Problemen gefunden werden, so dass ausführlichere Versuche interessante Erkenntnisse erbringen könnten. Es ist Anzunehmen,
dass Veränderungen sowohl an der Codierung und den evolutionären Verfahren als
auch an der Bewertung der Leistung vorgenommen werden müssen um praktikable
Ergebnisse gewinnen zu können.
184
15.4 Physiksimulation
15.4. Physiksimulation
Es wurde, wie bereits erläutert, in Erwägung gezogen, ein komplexes Modell der
Physik zur Bestimmung des Fahrverhaltens zu nutzen.
Zur Diskussion stand die Verwendung der OpenSource Physikengine ODE (Open
Dynamics Engine). Diese könnte zur Verfeinerung der Simulation genutzt werden,
um Lösungen zu finden, die leicht auf ein echtes Fahrzeug übertragbar sind. Die
grundlegenden Strukturen der Simulation können dabei erhalten bleiben. Fertige
Komponenten wie AIServer oder die View können weiterhin verwendet werden.
Die Verwendung einer solchen Physikengine geht zu lasten der Geschwindigkeit
der Simulation. Dafür lassen sich andere Situationen konstruieren und realistisch
erproben. Für weitere Informationen zu ODE steht die Webseite des Projektes (
http://ode.org ) zur Verfügung.
15.5. Fazit
Insgesamt bleibt festzustellen, das ”die Experimentiermethode der Evolution gleichfalls einer Evolution unterliegt” (I. Rechenberg). Prof. Rechenberg meinte mit dieser Aussage das nicht nur die momentane Lebensleistung eines Individuums für
das Überleben einer Art wichtig sei, sondern nach mehreren Generationen auch die
bessere Vererbungsstrategie, die eine schnellere Umweltanpassung zustandebringt,
ausgelesen und weiterentwickelt wird. Dieser Gedanke kann jedoch auch insofern zur
Interpretation herangezogen werden das die Forschung an evolutionären Algorithmen selbst ihre Evolution repräsentiert, d.h. die Strategien der evolutionären Algorithmen einer stetigen Weiterentwicklung durch die Forschung unterliegen. Dadurch
sind unzählige unterschliedliche Strategien für eine Erweiterung bzw. Verbesserung
dieser Art von Algorithmen existent2 . Dennoch bedarf es einer genauen Abwägung
der zu optimierenden bzw. lösenden Problemfelder, ob ein Einsatz solcher Erweiterungen sinnvoll ist, d.h. durch sie effizientere Optimierungen möglich sind.
Obwohl auch die Ideen aus vergangenen Tagen stammen sind genetische Algorithmen dennoch aktuell wie nie zuvor. Es gibt heutzutage keinen Bereich der nicht der
Optimierung oder Lösung komplexer Aufgaben bedarf; sei es in der Wirtschaft, Forschung oder auch dem Sport. So kann der in dieser Diplomarbeit entwickelte Server
für evolutionäre/genetische Verfahren für diverse Problemfelder verwendet werden
2
JunkDNS (vgl. Kapitel 3.2.3); Inversion, Dominanz und Diploidie (vgl. Kapitel 3.4.5)
185
15 Ausblick
und zukünftigen Projekten in der Forschung z.B. im Rahmen von studentischen Studienarbeiten als Basis dienen.
Dieser Diplomarbeit sollte die Nutzbarkeit der Verfahren zur Steuerung eines Fahrzeugs untersuchen. Zu diesem Zweck wurde eine Simulation entwickelt, die neben
dem primären Problem, dem Einparken unter verschiedenen Bedingungen, auch die
Konstruktion weiterer Szenarien ermöglicht. Es wurde dabei Wert darauf gelegt,
dass die Lernkomponente, also in diesem Fall der EAServer austauschbar ist. Dies
soll gegebenenfalls die Untersuchung anderer Verfahren für die selbe Problemstellung ermöglichen.
Auch wenn das Fahrzeugverhalten stark vereinfacht wurde um eine schnelle Berechnung zu ermöglichen, können mit dieser Simulation Problemlösungen gefunden
werden, die einen guten Ansatz zur Übertragung auf die wirkliche Welt darstellt.
Es ist so möglich eine vollständige Fahrzeugsteuerung für viele gängige Probleme zu
erschaffen und diese im simulierten Einsatz zu betrachten.
Die genetischen Verfahren haben sich, für das Lösen dieses Steuerungsproblems als
sehr effizient herausgestellt. Obwohl der Suchraum, der sich aus der Codierung ergibt, nicht durch Einfügen bekannten Wissens eingeschränkt wurde konnten für die
gestellten Probleme Lösungen gefunden werden. Dabei hat sich gezeigt, dass die
bekannten Standartverfahren ausreichend sind, die Effizients der Lösungsfindung
jedoch durch Einsatz verschiedener Erweiterungen verbessert werden kann.
186
A. Software Architekturen
Auf den folgenden Seiten werden Klassendiagramme, Sequenzdiagramme und andere
mit der Softwarearchitektur in Zusammenhang stehenden Bilder zusammengefasst
dargestellt. Die Beschreibungen zu den einzelnen Abbildungen sind in den vorangegangenen Kapiteln zu finden.
Es sind in diesem Kapitel folgende Abbildungen dargestellet:
1. Klassendiagramm: EALib-Bibliothek
2. Klassendiagramm: EAServer-Bibliothek
3. Auszug aus Klassendiagramm der Benutzeroberfläche
4. Nachrichtenorientierte Informationsverarbeitung
5. Sequenzdiagramm: Kommunikationsaufbaus und -abbaus
6. Sequenzdiagramm: Start und Terminierung des evolutionären Laufs
187
A Software Architekturen
Abbildung A.1.: Klassendiagramm: EALib-Bibliothek
188
Abbildung A.2.: Klassendiagramm: EAServer-Bibliothek
189
A Software Architekturen
Abbildung A.3.: Auszug aus Klassendiagramm der Benutzeroberfläche
190
Abbildung A.4.: Nachrichtenorientierte Informationsverarbeitung
191
A Software Architekturen
Abbildung A.5.: Sequenzdiagramm: Kommunikationsaufbaus und -abbaus
192
Abbildung A.6.: Sequenzdiagramm: Start und Terminierung des evolutionären Laufs
193
B. Literaturverzeichnis
[AS97]
A.Geyer-Schulz. Fuzzy Rule-Based Expert Systems and Genetic Machine
Learning. Physica Verlag, Heidelberg, zweite überarbeitete und erweiterte
edition, 1997.
[B+ 04]
J. Blanchette et al. C++ GUI-Programmierung mit Qt3. Addison Wesley,
München, 2004.
[Eck04a] Prof. Dr. R. Eck. Vorlesungsskript Softcomputing. Georg-Simon-Ohm
Fachhochschule, Nürnberg, 2004.
[Eck04b] Prof. Dr. R. Eck. Vorlesungsskript Software Engineering 1. Georg-SimonOhm Fachhochschule, Nürnberg, 2004.
[Erl02]
Dr. T. Erler. UML Das Einsteigerseminar. VMI Buch, Bonn, erste edition,
2002.
[Fur95]
T. Furuhashi. Advances in Fuzzy Logic, Neural Networks and Genetic
Algorithms. Springer Verlag, Berlin, Heidelberg, New York, 1995.
[G+ 00]
G. Görz et al. Handbuch der Künstlichen Intelligenz. Oldenbourg, München, dritte vollständig überarbeitete edition, 2000.
[G+ 04]
E. Gamma et al. Entwurfsmuster - Elemente wiederverwendbarer Software.
Addison Wesley, München, 2004.
[Gol89]
D. E. Goldberg. Genetic Algorithms in Search Optimization and Machine
Learning. Addison Wesley, New York, 1989.
[Jes02]
R. Jesse. Java Swing Das Einsteigerseminar. VMI Buch, Bonn, erste
edition, 2002.
[K+ 90]
Y. Kodratoff et al. Machine Learning - An Artifical Intelligence Approach,
volume 3. Morgan Kaufmann Publisher Inc., San Mateo, 1990.
195
B. Literaturverzeichnis
[Kle05]
M. K. Klemke. Den garbage collector der jvm richtig nutzen. IX - Magazin
für professionelle Informationstechnik, (4):102–106, 4 2005.
[Krü02] G. Krüger. Handbuch der Java-Programmierung. Addison Wesley, München, dritte edition, 2002.
[Mic96]
Z. Michalewicz. Genetic Algorithms + Data Structures = Evolution Programs. Springer Verlag, Berlin, Heidelberg, New York, dritte überarbeitete
und erweiterte edition, 1996.
[P+ 95]
D. W. Pearson et al. Artifical Neural Nets and Genetic Algorithms. Springer Verlag, Wien, New York, 1995.
[PTH]
http://sourceware.org/pthreads-win32.
[R+ 99]
R. Roy et al. Advances in Soft Computing - Engineering Design and Manufactoring. Springer Verlag, London, 1999.
[Sch04a] Prof. Dr. C. Schiedermeier. Vorlesungsskript Computergrafik.
Simon-Ohm Fachhochschule, Nürnberg, 2004.
Georg-
[Sch04b] Prof. Dr. C. Schiedermeier. Vorlesungsskript Software Engineering 2.
Georg-Simon-Ohm Fachhochschule, Nürnberg, 2004.
[Ste05]
B. Steppan. Codewrapper für java-anwendungen. IX - Magazin für professionelle Informationstechnik, (4):74–76, 4 2005.
[Str00]
B. Stroustrup. Die C++ Programmiersprache. Addison Wesley, München,
vierte aktualisierte und erweiterte edition, 2000.
[Ull04]
C. Ullenboom. Java ist auch eine Insel. Galileo Computing, vierte aktualisierte und erweiterte edition, 2004.
[WIK]
http://de.wikipedia.org.
[Z+ 04]
W. Zuser et al. Software Engineering mit UML und dem Unified Process.
Pearson Studium, München, zweite überarbeitete edition, 2004.
196
Erklärung
Wir versichern, dass wir die Arbeit ohne fremde Hilfe und ohne Benutzung anderer
als der erwähnten Quellen angefertigt haben, und dass die Arbeit in gleicher oder
ähnlicher Form noch keiner anderen Prüfungsbehörde vergelegt hat und von dieser
als Teil einer Prüfungsleistung angenommen wurde.
Alle Ausführungen, die wörtlich oder sinngemäß übernommen wurden, sind als solche gekennzeichnet.
Andreas Blinzler
Andreas Hirschberger
197