Aufgabe ¨U2 - TU Clausthal/IEE

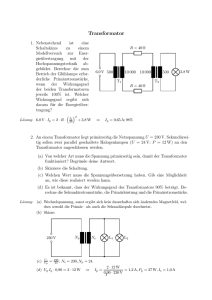
Grundlagen der Elektrotechnik II:
Große Übung – Transformator
Aufgabe Ü2
Ein Widerstand von R = 100 Ω soll eine Leistung von 10 kW aufnehmen. Der Widerstand wird
über einen idealen Transformator an das Wechselstromnetz (230 V, 50 Hz) angeschlossen.
1. Wie groß ist bei einer primären Windungszahl von N1 = 1000 die Windungszahl der
Sekundärseite N2 zu wählen?
2. Mit welchem (auf der Primärseite) wirksamen Widerstand wird das Netz belastet?
3. Welche Leistung nimmt der Verbraucher bei gleicher Spannung U , aber f = 60 Hz bzw.
f = 0 Hz auf?
1. Berechnung der sekundären Windungszahl:
Der ideale Transformator wird als verlustfrei
U1
N1
N2
U2
betrachtet. Es werden daher nur die primär-
R
und die sekundärseitigen Windungen (N1
und N2 ) gezeichnet.
Die vom Widerstand auf genommene Leistung ist abhängig von der sekudärseitigen Spannung.
Aus der Bedingung, dass der Widerstand eine Leistung von 10 kW aufnehmen soll, ergibt sich
der Betrag der Spannung U2 .
P =
√
√
U22
⇒ U2 = P · R = 10 kW · 100 Ω = 1000 V
R
Aus der sekundärseitigen Spannung wird das notwendige Übersetzungverhältnis und daraus die
Windungszahl der Sekundärspule berechnet:
ü =
N1
U1
230 V
=
⇒ ü =
= 0,23
N2
U2
1000 V
N1
1000
N2 =
=
= 4348
ü
0,23
Die Windungszahl der Sekundärseite beträgt 4348.
SS 2014
1
Verena Schild, 7. Juli 2014
Grundlagen der Elektrotechnik II:
Große Übung – Transformator
2. Berechnung des primärseitig wirkenden Widerstandes:
Die auf der Primärseite aufgenommene (Schein-)Leistung ist bei einem verlustlosen Transformator
genauso groß, wie die auf der Sekundärseite abgegebene (Schein-)Leistung. Daraus ergibt sich
die Umrechnungsvorschrift, mit der der Widerstand der Sekundärseite auf die Primärseite
umgerechnet wird.
Aus der Maschengleichung und der Annahme idealer
”
Transformator“ folgt:
Iµ
U1
U 1 = U 02
U 02
Xh
2
1
2
2
U
U
=
0
R2
R2
R
und
⇒
S1 = S2
R20 =
U12
· R2 = ü2 · R2
U22
Mit eingesetzten Zahlenwerten ergibt sich:
R0 = ü2 · R = 0,232 · 100 Ω = 5,29 Ω
3. Leistungsaufnahme bei 60 Hz bzw. bei 0 Hz:
1. Fall: f = 60 Hz
Die Transformatorentwurfsgleichung gibt den Zusammenhang zwischen dem Betrag und der
Frequenz der Spannung, der Windungszahl und dem magnetischen Fluss an (vgl. Lösung zu
Aufgabe Ü1):
U1 = 4,44 · N1 · f · Φ̂
⇒
Φ̂ =
U1
4,44 · N1 · f
Bei konstanter Spannung U1 wird demnach mit steigender Frequenz der Fluss kleiner. Eine
Erhöhung der Frequenz ist somit für Transformatoren im Allgemeinen unproblematisch, da mit
steigender Frequenz der Magnetisierungsstrom und damit der magnetische Fluss sinken.
Für den Betrag der sekundärseitigen Spannung U2 ergibt sich durch Einsetzen der oben abgeleiteten Gleichung für Φ̂:
U2 = 4,44 · N2 · f · Φ̂ = 4,44 · N2 · f ·
U1
N2
=
· U1
4,44 · N1 · f
N1
Das Übersetzungsverhältnis ist somit unabhängig von der Frequenz. Da die Belastungsimpedanz
unabhängig von der Frequenz ist, bleibt die aufgenommene (Wirk-)Leistung konstant, da ü, U1
und damit auch U2 konstant bleiben.
SS 2014
2
Verena Schild, 7. Juli 2014
Grundlagen der Elektrotechnik II:
Große Übung – Transformator
Iµ
Aus dem Ersatzschaltbild lässt sich entnehmen, dass
der Magnetisierungsstrom I µ mit steigender Frequenz
U1
0
Xh
U2
sinkt, da sich der Blindwiderstand Xh mit steigender
Frequenz erhöht. Der Betrag der Spannung U20 bleibt
dabei unverändert.
2. Fall: f = 0 Hz
Für f = 0 Hz (Gleichspannung) stellt die Hauptinduktivität Xh im eingeschwungenen Zustand
einen Kurzschluss dar, wodurch U20 = 0 wird.
Ein Transformator funktioniert nicht mit Gleichspannung! Die Last nimmt keinen Leistung auf.
Werden Übergangsvorgänge beim Einschalten des Gleichstroms berücksichtigt, so ergeben sich bei
einem verlustbehafteten Transformator (mit verlustbehafteten Spulen) die folgenden Verhältnisse:
i(t), Φ(t)
u1 (t)
R
i(t)
U1
R
X1
X2
U2
t
u2 (t)
Ersatzschaltbild mit verlustbehafteter Spule auf
der Primärseite.
t
Der Strom i(t) steigt nach dem Einschalten der Gleichspannung nach einer Exponentialfunktion
an und erreicht nach etwa drei bis fünf Zeitkonstanten (T = L/R) den stationären Endwert
i(t) = U/R = const.
Da der Fluss Φ(t) proportional zum Strom ist (Durchflutungsgesetz), wird mit dem Erreichen
des stationären Endwerts für den Strom auch der Fluss konstant und in der Sekundärspule wird
keine Spannung mehr induziert (Induktionsgesetz).
SS 2014
3
Verena Schild, 7. Juli 2014
Grundlagen der Elektrotechnik II:
Große Übung – Transformator
Wird ein idealer Transformator (ohne ohmschen Wicklungswiderstand) betrachtet, ergibt sich
folgendes:
i(t), Φ(t)
i(t)
U1
R
X1
X2
U2
t
u2 (t)
Ersatzschaltbild mit idealer Spule (ohne
Wicklungswiderstand).
t
Für die induzierte Spannung der Spule 1 (die angelegte Gleichspannung), gilt nach dem Induktionsgesetz:
U1 = Lh ·
di(t)
dΦ(t)
= N1 ·
dt
dt
Daraus ergibt sich für den Strom und den magentischen Fluss:
Z
Z
U1
U1
U1
i(t) =
dt =
dt =
·t
L
Lh
Lh
Z
Z h
U1
U1
U1
dt =
dt =
·t
Φ(t) =
N1
N1
N1
Der Strom i(t) und der magnetische Fluss Φ(t) steigen somit linear mit der Zeit an. Die
Flussänderung ist also konstant und damit ist auch die in der Sekundärspule induzierte Spannung
U2 konstant.
dΦ
d
U2 = N2 ·
= N2 ·
dt
dt
U1
N1
=
N1
· U1
N2
Für die Sekundärspannung ergibt sich somit ein zeitunabhängiger Verlauf (Gleichspannung).
Dies gilt jeodch nur für einen idealen Transformator ohne Wicklungswiderstände (R1 = R2 = 0)
und einem magnetischen Widerstand des Eisens, der unabhängig von der Flussdichte ist (keine
Sättigung).
SS 2014
4
Verena Schild, 7. Juli 2014
Grundlagen der Elektrotechnik II:
Große Übung – Transformator
Bei einem verlustbehafteten Transformator steigen Magnetisierungsstrom und magnetischer Fluss,
wie oben gezeigt, nicht linear sondern entsprechend einer Exponentialfunktion an, sodass die
sekundärseitige Spannung nicht konstant ist, sondern exponentiell abfällt. Im Einschaltaugenblick
ergibt sich jedoch auch bei einem verlustbehafteten Transformator bei Gleichspannung auf der
Primärseite die Sekundärspannung direkt aus dem Übersetzungsverhältnis.
SS 2014
5
Verena Schild, 7. Juli 2014