Aufgabe 1: Elektrisches Feld Ein Metallring wird in das Feld des

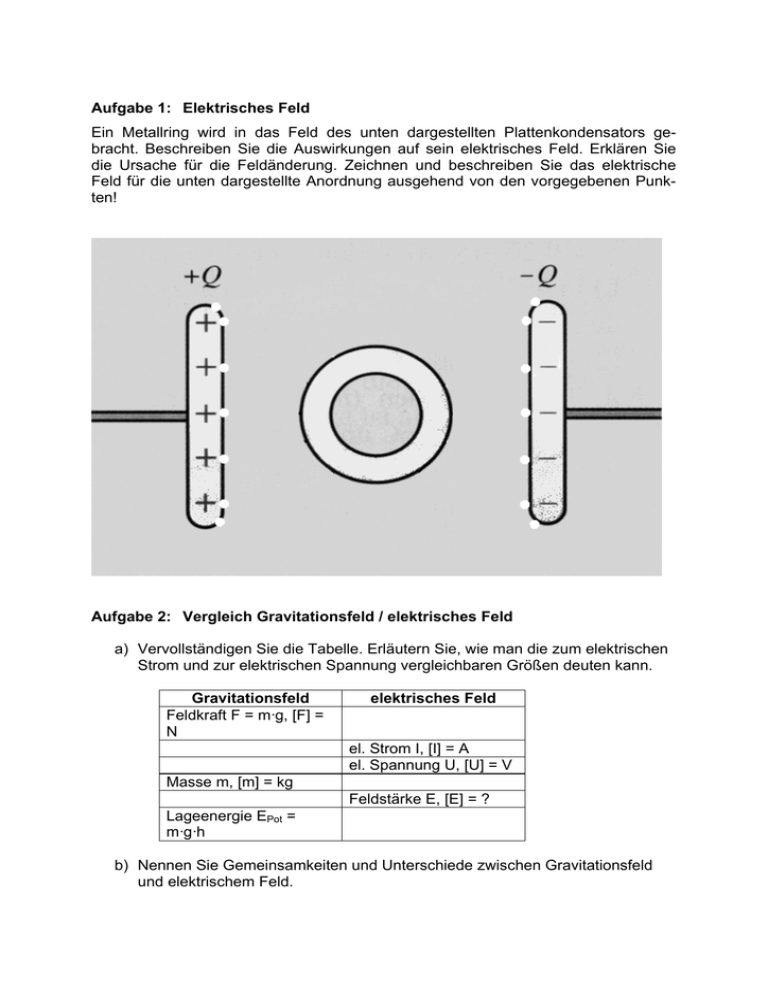
Aufgabe 1: Elektrisches Feld
Ein Metallring wird in das Feld des unten dargestellten Plattenkondensators gebracht. Beschreiben Sie die Auswirkungen auf sein elektrisches Feld. Erklären Sie
die Ursache für die Feldänderung. Zeichnen und beschreiben Sie das elektrische
Feld für die unten dargestellte Anordnung ausgehend von den vorgegebenen Punkten!
Aufgabe 2: Vergleich Gravitationsfeld / elektrisches Feld
a) Vervollständigen Sie die Tabelle. Erläutern Sie, wie man die zum elektrischen
Strom und zur elektrischen Spannung vergleichbaren Größen deuten kann.
Gravitationsfeld
Feldkraft F = m·g, [F] =
N
elektrisches Feld
el. Strom I, [I] = A
el. Spannung U, [U] = V
Masse m, [m] = kg
Feldstärke E, [E] = ?
Lageenergie EPot =
m·g·h
b) Nennen Sie Gemeinsamkeiten und Unterschiede zwischen Gravitationsfeld
und elektrischem Feld.
Aufgabe 3: Messung elektrischer Felder
Nennen Sie verschiedene Methoden zur Messung der Feldstärke zwischen den Platten eines Plattenkondensators (ausgehend von den im Unterricht behandelten Versuchen).
Aufgabe 4: Ladung
a) Berechnen Sie die Ladung, die insgesamt durch den Leiterquerschnitt geflossen ist, wenn 6 min und 8 s lang die konstante Stromstärke I = 1,7 mA gemessen wurde.
b) Erläutern Sie, wie sich im t-Q-Diagramm die Stromstärke zu einem bestimmten Zeitpunkt t ablesen lässt.
Aufgabe 5: Elektrische Kraft
Ein elektrisches Feld der Stärke 160 N/C sei senkrecht zur Erdoberfläche nach unten
gerichtet.
a) Vergleichen Sie die elektrostatische Kraft auf ein Elektron (q = -1,6·10-19 C,
m = 9,1·10–31 kg) mit der nach unten gerichteten Gravitationskraft und bestimmen Sie den Betrag und die Richtung der Beschleunigung, die das Elektron
erfährt.
b) Bestimmen Sie die Ladung einer Münze der Masse m = 3 g so, dass die durch
dieses Feld bewirkte Kraft die Gravitationskraft ausgleicht.
Aufgabe 6: Spannung
Ein Wattestück hat die Masse m = 0,02 g und die Ladung q = 0,17 nC.
a) Berechnen Sie die Geschwindigkeit, die es erreichen würde, wenn es im Vakuum die Spannung U = 110 kV durchliefe.
b) Berechnen Sie wie groß die Spannung zwischen waagerecht liegenden Kondensatorplatten vom Abstand 2,5 dm sein müsste, damit das Wattestück darin
schwebt.