1.4. Das homogene elektrische Feld

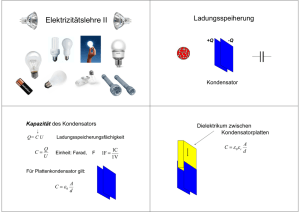
1.4. Das homogene elektrische Feld
1.4.1. Arbeit und Energie im homogenen el. Feld eines Plattenkondensators
+
+ s
-
Verschiebt das Feld eine Probeladung Q um ein Wegstück s,
so verrichtet das Feld die Arbeit
W = F · s = Qprobe · E · s
Die vom Feld verrichtete Arbeit ist gleich der Änderung ( hier
Verminderung) der potentiellen Energie. Vergleiche: fallender
Körper im Gravitationsfeld .
d
Wird die Ladung von einer Platte auf die andere verschoben, so gilt s = d. Ferner gilt dann für die
el. Arbeit: W = U ·I · t = U · Q
Damit erhält man im hom . Feld:
E=
U
d
1.4.2. Potenzial (a function of position in space )
Um einen Punkt im Feld unabhängig von der Ladung kennzeichnen zu können führt man den
Begriff des Potenzials ein.
W 12
Der Quotient
heißt elektrische Potentialdifferenz des el. Feldes von Punkt 1 bezüglich
Q
des Bezugspunktes 2:
Φ12 = Φ1 - Φ2 =
W 12 Q E s 12
=
=Es 12=U 12
Q
Q
Das Potenzial ist vergleichbar mit dem Druck im Wasserrohr oder der Höhe im Gravitationsfeld,
die Spannung (Potenzialdifferenz) mit dem Druckunterschied.
Dem Bezugspunkt P2 gibt man gewöhnlich das Potenzial 0.
Stellen gleichen Potenzials ergeben Linien oder Flächen, sogenannte Äquipotenziallinien
(flächen). Verschiebt man Ladungen entlang von Äquipotenziallinien so ist dazu keine Arbeit nötig.
(vgl. Wandern auf gleicher Höhe)
+
Bsp.
1
2
W12 = W13 = W14
Die Punkte 2,3,4 liegen auf gleichem Potenzial.
3
4
Äquipotenziallinien und Feldlinien schneiden sich
senkrecht. Verschiebt man eine Ladung auf einer
Potenziallinie, so wird, nach Definition, keine Arbe
verrichtet. Die Kraft muss also senkrecht zur
Bewegungsrichtung sein.
+
-
Messung von Äquipotentiallinien
Demoversuch:
In ein Wassertrog werden mit Hilfe eines Voltmeters Äquipotentiallinien aufgenommen.
Wasser
V
6V
Praxis:
Äqipotentiallinien am
Körper werden beim
EKG ausgenutzt
1.4.3. Plattenkondensator als Ladungsspeicher
Zwei isoliert aufgestellte Leiter heißen Kondensator. Kondensatoren dienen häufig als Ladungsspeicher.
Kugel­ , Platten­ , Zylinderkondensator Messung der Speicherkapazität (Buch S 21)
Q
V
Messreihe
U in V
50
100
150
200
250
Q in nC
Der konstante Quotient Q/U heißt Kapazität C. Also
[C] = 1 AsV -1 = 1 F (Farad)
C=
Q
U
300
Eine spezielle Formel für die Kapazität des Plattenkondensators in Abhängigkeit von der Geometrie
Versuchsaufbau wie oben!
Wissen: Q ~ U
Ferner gilt : Q ~ A (triv) Bleibt noch: Q in Abh. Vom Plattenabstand (U = 100 V konstant)
Q in nC
d in mm
2
4
6
8
oder Q=o
A
U
d
o heißt el.Feldkonstante oder Dielktrizitätskonstante. [ o ] = Asm­1V­1 Literaturwert : 8,85 . 10 ­12 CV­1m­1
Wegen Q
=C folgt : U
C= o
A
d
Musteraufgabe:
Wie ändern sich die Größen Q, U und C in Abhängigkeit vom Abstand d, wenn der Kondensator
–
an der Spannungsquelle angeschlossen bleibt und dann der Abstand d verdoppelt wird ?
–
Von der Spannungsquelle getrennt wird und dann der Abstand d verdoppelt wird ?
1.4.4. Schaltung von Kondensatoren
Parallelschaltung:
Qges = Q1 + Q2
→
UgesCges = U1C1 + U2C2
→ Cges = C1 + C2
Reihenschaltung:
1.4.5. Anwendungen
- Kondensatormikrophon
- Glättung von pulsierender Gleichspannung
wegen U konstant