Klasse 10mn / 11ns: Mechanik: Kinematik einfacher geradliniger

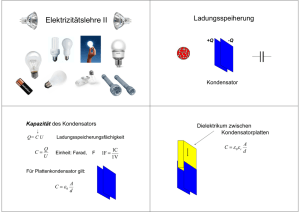
Physik ∙ Kursstufe ∙ Elektromagnetismus ∙ 1.1.6. Kondensatoren
1.1.6 Kondensatoren
Ein Kondensator ist ein Bauteil, das aus zwei
elektrisch leitenden Flächen besteht, zwischen
denen sich ein Isolator (auch Dielektrikum
genannt) befindet. Ein Kondensator kann u. a.
dazu dienen, elektrische Ladung zu speichern.
Kondensatoren gibt es in sehr vielen
verschiedenen Bauarten und Bauformen (s. Abb.).
Erste Frage: Welcher Zusammenhang besteht zwischen Ladung Q
und Feldstärke E bei einem Kondensator?
Dazu betrachten wir einen Plattenkondensator (PK), der auf der Oberfläche
A der linken Platte die Überschussladung +Q und auf der rechten Platte die
Überschussladung –Q trägt (felderzeugende Ladung).
Wir überlegen uns: Wenn man einen zweiten gleichen PK
neben den ersten platziert, so dass sich die Fläche A
verdoppelt, würde sich die felderzeugende Ladung Q
verdoppeln, aber die Feldstärke E konstant bleiben
(homogenes Feld).
Also hängt E nicht unmittelbar von Q ab! Da aber Q proportional zur Fläche A ist, ergibt sich
eine neue Größe, die mit E zusammen hängt:
a) Die Flächendichte σ von Q
Da Q~A, ist der Quotient Q/A konstant. Wir nennen ihn die Flächendichte (Flächenladungsdichte) σ.
Es gilt:  
Q
A
(1)
Die Einheit von σ ist C/m². Wenn man nun σ und E misst, stellt man fest, dass
sie proportional zueinander sind. Der Quotient σ/E ist somit konstant und heißt
b) Die elektrische Feldkonstante ε0
Es gilt im Vakuum und näherungsweise in Luft:

C


8
,
85

10

12
0
E
(2)
Vm
)
Nun können wir die erste Frage beantworten:
 Q

0 A0 , d.h. bei konstanter Fläche A sind E und Q proportional zueinander.
E
Zweite Frage: Wie lässt sich die Ladungsmenge Q bestimmen, die ein Kondensator speichern kann?
Eine Messung zeigt: Je höher die anliegende Spannung U, desto größer die Überschussladung Q auf den
Platten. Es gilt: Q~U und damit ist der Quotient Q/U konstant. Da der Quotient angibt, wie viel Ladung pro
Volt ein Kondensator aufnehmen kann, nennen wir diese Größe die
a) die Kapazität C eines Kondensators
Es gilt allgemein für alle Kondensatoren: C 
Q
U
Die
C
.
V
Einheit der Kapazität C heißt Farad (nach Michael Faraday). Es gilt: 1F  1
Für einen Plattenkondensator mit Luft (oder Vakuum) zwischen den Platten folgt mit Hilfe der
Gleichungen (1) und (2):
Q
A
C
 

A Das bedeutet, je größer die Plattenfläche und je kleiner der Plattenabstand, desto
UE
d
d
0
mehr Ladung kann ein PK speichern. Bei bekannter Kapazität lässt sich die Ladung nun berechnen mit:
Q  C U
Physik ∙ Kursstufe ∙ Elektromagnetismus ∙ 1.1.6. Kondensatoren
Nun wollen wir auch Kondensatoren betrachten, deren Plattenzwischenraum mit einem anderen
(nichtleitenden) Stoff als Luft bzw. Vakuum gefüllt ist:
b) Kondensator mit Dielektrikum
Messungen zeigen, dass ein mit einem Isolator (Dielektrikum) gefüllter Kondensator bei gleicher Spannung
mehr Ladungsmenge aufnehmen kann als ein luftgefüllter, d.h. eine höhere Kapazität besitzt.
Das Verhältnis der beiden Kapazitäten Cmit und Cohne hängt nur vom Material ab und heißt die
Dielektrizitätszahl εr.
C
mit
Somit gilt: r  C
.
Tabelle mit einigen Werten:
ohne
Die Kapazität eines Plattenkondensators mit einem Dielektrikum, das die
Dielektrizitätszahl εr besitzt, beträgt dann:


A
C


C

0

mit
r
ohne
r
d
Wir können nun auch Gleichung (2) verallgemeinern und erhalten die
Stoff
Keramik
Glas
H2O
Alkohol
Benzol
Luft
Vakuum
εr
80 ... 1000
5-9
81
25,8
2,3
1,0006
1
c) Die Grundgleichung der Elektrostatik
Im Dielektrikum gilt: 0r 

E
Aufgaben
1
Ein luftgefüllter Plattenkondensator (Fläche A = 2,0 dm2; Plattenabstand d = 3,0 mm) wird mit der
Stromquelle der Spannung U = 250 V aufgeladen und dann von der Quelle getrennt.
a) Welche Kapazität besitzt dieser Kondensator und welche elektrische Feldstärke E herrscht zwischen den
Platten?
b) Wie viele Elementarladungen trägt die negativ geladene Kondensatorplatte?
c) Welche potentielle Energie gewinnt oder verliert ein Elektron, wenn es von der negativen zur positiven
Platte bewegt wird? Gib den Wert auch in Elektronenvolt (eV) an.
d) Nun wird bei dem von der Quelle getrennten Kondensator der Plattenabstand verdoppelt (d´ = 6,0 mm).
Welche Kapazität C´ hat der Kondensator nun und welche Feldstärke E´ herrscht zwischen den Platten.
2
In das homogene Feld eines Plattenkondensators (E=2 ,5kN/C) wird die positive Probeladung

15
q3
,210
Cgebracht. Die Platten des luftgefüllten Plattenkondensators haben einen Abstand von 4,0
cm.
a) Gib die Richtung der Kraft bezüglich der Platten an, die auf die Probeladung wirkt.
b) Berechne die Kraft, die auf die Probeladung wirkt.
c) Berechne die verrichtete Arbeit, wenn die Ladung von der negativen zur positiven Platte geführt wird.

10
,210
C
Der Kondensator hat selbst eine Ladung von Q2
gespeichert.
d) Berechne die Spannung, die am Plattenkondensator anliegt.
e) Berechne die Plattenfläche des Plattenkondensators.
Physik ∙ Kursstufe ∙ Elektromagnetismus ∙ 1.1.6. Kondensatoren