Übungsblatt 1

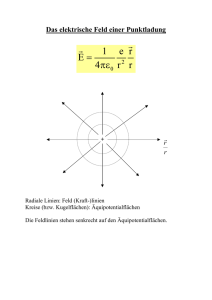
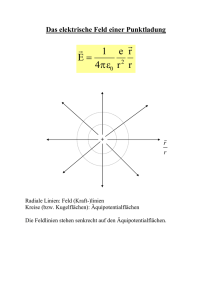
Physik für Ingenieure II (PH2)
WS 2015/16
Dozentin: Prof. Dr. A. Köhler
Übung: Alexander Rudnick, Fabian Panzer, Julian Kahle
Ausgabe: Fr, 16.10.2015
Korrektur: Fr, 23.10.2015
Übungsblatt 1
Aufgabe 1: Coulombkraft
Positive Ladungen von welchen (gleichen) Beträgen müsste man auf Erde und Mond jeweils
bringen, um die Gravitationsanziehung zwischen beiden zu kompensieren? Benötigen Sie zur
Lösung dieser Aufgabe die Entfernung zwischen Erde und Mond? Warum bzw. warum nicht?
Die Masse der Erde beträgt M = 5, 98 · 1024 kg, die des Mondes m = 7, 36 · 1022 kg. Die
2
Gravitationskonstante ist G = 6, 67 · 10−11 Nkgm2 . (∗)
Aufgabe 2: Elektrische Felder
Nebenstehende Abbildung zeigt ein Feldlinienbild.
Der Feldlinienabstand auf der linken Seite ist doppelt so groß wie der Abstand auf der rechten Seite.
a) Der Betrag des elektrischen Feldes im Punkt A
sei 40, 0 N
C . Welche elektrostatische Kraft wirkt
auf ein Proton im Punkt A? (∗)
b) Welchen Betrag hat das Feld im Punkt B? (∗)
Betrachten Sie nun eine dünne, kreisförmige, homogen geladene Scheibe mit dem Radius R.
a) Skizzieren Sie qualitativ die elektrischen Feldlinien. (∗∗)
Hinweis zu c): Betrachten Sie als Grenzfälle einerseits sehr nahe bei der Scheibe gelegene Punkte,
wo das elektrische Feld senkrecht auf der Oberfläche der Scheibe steht, andererseits sehr weit
von der Scheibe entfernte Punkte, wo sich das Feld der Scheibe dem Feld einer Punktladung
annähert.
Aufgabe 3: Gauß’scher Satz
Eine massive, nichtleitende Kugel mit dem Radius R ist homogen geladen mit einer konstanten
Raumladungsdichte ρ. Die Gesamtladung der Kugel betrage Q.
a) Berechnen Sie den Betrag des elektrischen Feldes außerhalb der Kugel (r > R mit r:
Abstand vom Kugelmittelpunkt). (∗∗)
b) Zeigen Sie, dass der Betrag des elektrischen innerhalb der Kugel gegeben ist durch:
E=
Q r
4π0 R3
(1)
3
Verwenden Sie, dass die Ladung im Inneren der Kugel gegeben ist durch Qin (r) = Q · Rr 3 .
(∗∗)
c) Skizzieren Sie den Betrag des elektrischen Feldes als Funktion von r. (∗)
1
Aufgabe 4: Potentialdifferenz
Die Potentialdifferenz zwischen einer Wolke und Erde bei einem Blitz, der eine Ladung von 30 C
transportiert, betrage 1, 0 · 109 V .
a) Um welchen Betrag vermindert sich die Energie der Ladung bei ihrem Transport von der
Wolke zur Erde? (∗)
b) Auf welche Endgeschwindigkeit könnte man mit dieser Energie ein Auto der Masse 1000 kg
aus der Ruhe beschleunigen? (∗)
Aufgabe 5: Plattenkondensator
Die Platten eines Kondensators seien planparallel und kreisförmig mit dem Radius 8, 2 cm und
einem Abstand von 1, 3 mm.
a) Berechnen Sie die Kapazität des Kondensators. (∗)
b) Welche Ladung befindet sich auf den Platten, wenn man eine Potentialdifferenz von 120 V
anlegt? (∗)
Aufgabe 6: Gesamtkapazität
Bestimmen Sie die äquivalente Kapazität der Kondensatorschaltung in nebenstehender Abbildung. Die
Kapazitäten der einzelnen Kondensatoren seien gegeben zu C1 = 10, 0 µF , C2 = 5, 00 µF und C3 =
4, 00 µF . (∗)
Aufgabe 7: Elektrischer Widerstand
Der Widerstand eines 2, 0 m langen Drahtes mit einem Durchmesser von 1, 0 mm betrage 50 mΩ.
Berechnen Sie den spezifischen Widerstand des Drahtmaterials. (∗)
Aufgabe 8: Elektrische Leistung
Eine Potentialdifferenz von 120 V versorgt einen Raumheizer, dessen Widerstand im warmen
Zustand 14 Ω beträgt.
a) Mit welcher Rate (=Energie/Zeit) wird in diesem Gerät elektrische Energie in Wärme
umgewandelt? (∗)
b) Wie hoch sind die Stromkosten bei einer Betriebsdauer von 5, 0 h, wenn der Strompreis
5, 0 ct/kW h beträgt? (∗)
2