to the PDF file.

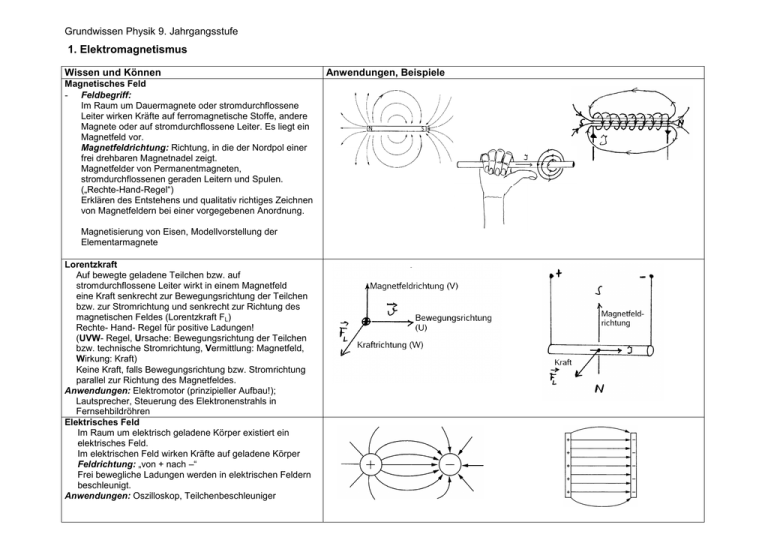
Grundwissen Physik 9. Jahrgangsstufe
1. Elektromagnetismus
Wissen und Können
Magnetisches Feld
- Feldbegriff:
Im Raum um Dauermagnete oder stromdurchflossene
Leiter wirken Kräfte auf ferromagnetische Stoffe, andere
Magnete oder auf stromdurchflossene Leiter. Es liegt ein
Magnetfeld vor.
Magnetfeldrichtung: Richtung, in die der Nordpol einer
frei drehbaren Magnetnadel zeigt.
Magnetfelder von Permanentmagneten,
stromdurchflossenen geraden Leitern und Spulen.
(„Rechte-Hand-Regel“)
Erklären des Entstehens und qualitativ richtiges Zeichnen
von Magnetfeldern bei einer vorgegebenen Anordnung.
Magnetisierung von Eisen, Modellvorstellung der
Elementarmagnete
Lorentzkraft
Auf bewegte geladene Teilchen bzw. auf
stromdurchflossene Leiter wirkt in einem Magnetfeld
eine Kraft senkrecht zur Bewegungsrichtung der Teilchen
bzw. zur Stromrichtung und senkrecht zur Richtung des
magnetischen Feldes (Lorentzkraft FL)
Rechte- Hand- Regel für positive Ladungen!
(UVW- Regel, Ursache: Bewegungsrichtung der Teilchen
bzw. technische Stromrichtung, Vermittlung: Magnetfeld,
Wirkung: Kraft)
Keine Kraft, falls Bewegungsrichtung bzw. Stromrichtung
parallel zur Richtung des Magnetfeldes.
Anwendungen: Elektromotor (prinzipieller Aufbau!);
Lautsprecher, Steuerung des Elektronenstrahls in
Fernsehbildröhren
Elektrisches Feld
Im Raum um elektrisch geladene Körper existiert ein
elektrisches Feld.
Im elektrischen Feld wirken Kräfte auf geladene Körper
Feldrichtung: „von + nach –“
Frei bewegliche Ladungen werden in elektrischen Feldern
beschleunigt.
Anwendungen: Oszilloskop, Teilchenbeschleuniger
Anwendungen, Beispiele
Elektromagnetische Induktion
Bewegt man einen Leiter im Magnetfeld quer zur
Feldrichtung, so wird zwischen den Leiterenden eine
Spannung induziert.
Ebenso gilt:
Verändert sich das von einer Spule umfasste Magnetfeld,
so wird zwischen den Spulenenden eine Spannung
induziert. In einem geschlossenen Stromkreis fließt ein
Induktionsstrom.
Lenzsche Regel: Der Induktionsstrom ist stets so gerichtet, Relativbewegung Spule – Magnet
dass er seiner Ursache entgegenwirkt. (Energieerhaltung!)
Änderung der Stärke des Magnetfelds
Anwendungen:
Transformator, Generator
relativ verlustarmer Energietransport mit Hilfe der
Hochspannungstechnik
2. Atome
Wissen und Können
Anwendungen, Beispiele
Aufbau der Atome
Atome bestehen aus einer negativ geladenen Atomhülle
mit Elektronen sowie einem positiv geladenen
Atomkern mit Protonen und Neutronen.
56
26 Fe
A
Z X
;
X: Name des Elements
A: Massenzahl
Z: Kernladungszahl oder Ordnungszahl
Struktur und Größenverhältnisse kann man experimentell
untersuchen (Ölfleckversuch; Streuversuche von Rutherford; Elektronenstreuung).
Größenordnungen
-10
Atom
10 m
-14
Kern
10 m
-15
Proton 10 m
-18
Quark
< 10 m
:
Eisen, 26 Protonen (und auch Elektronen), 30 Neutronen
Protonen und Neutronen zusammen werden auch als Nukleonen bezeichnet.
Rutherfordscher Streuversuch:
Aufnahme und Abgabe von Licht
Spektren von Licht
Analysiert man Lichtquellen, indem man mit Prismen oder
Gittern Spektren erzeugt, so erkennt man verschiedene
Arten von Spektren:
Kontinuierliches Spektrum (Glüh- oder Kohlebogenlampe)
Linienspektrum (Quecksilber-, Natriumdampflampe)
Absorptionsspektrum (weißes Licht durch best. Gase)
diskrete Energiestufen in der Atomhülle
Atome sind in der Lage ganz bestimmte Energieportionen
aufzunehmen (absorbieren) beziehungsweise abzugeben
(emittieren). Diese Energieportionen treten in
Form von Photonen (Lichtquanten) auf.
Übergänge in der äußeren Elektronenhülle stehen im
Zusammenhang mit Photonen des sichtbaren Lichtes
-19
(Energie: einige Elektronenvolt; 1eV = 1,6 10 J).
Übergänge in der inneren Elektronenhülle stehen im
Zusammenhang mit Photonen von Röntgenstrahlung
(Energie: einige keV).
Strahlung radioaktiver Nuklide und Kernumwandlungen
Man kennt drei Arten radioaktiver Strahlung:
α-Strahlung: Heliumkerne
β-Strahlung: Elektronen
γ-Strahlung: sehr energiereiche Photonen
Der Nachweis erfolgt meist über die ionisierende Wirkung
der Strahlung (Zählrohr; Film)
Ursache der Strahlung ist meist der Zerfall instabiler Kerne.
Die Zeit, in der die Hälfte einer Anzahl radioaktiver Kerne
zerfällt, heißt Halbwertszeit t.
Kernspaltung: Aufspaltung eines schweren Kerns in zwei
mittelschwere (Möglichkeit der Kettenreaktion)
Kernfusion: Verschmelzung von zwei leichten Atomkernen
zu einem schwereren.
Beiden Reaktionen gemein sind folgende Punkte:
Masse der Edukte > Masse der Produkte
•
Die Differenz heißt Massendefekt ∆m
•
2
Freiwerdende Energie pro Prozess: E = ∆m c
•
Am stabilsten sind mittelschwere Kerne (z.B. Eisen)
•
Emission und Absorption:
aufzunehmen beziehungsweise abzugeben. Damit sind immer Prozesse in der Elektronenhülle verbunden.
Ablenkung radioaktiver Strahlung im Magnetfeld:
Spaltung:
1
235
236
89
144
0 n + 92 U → 92 U → 36 Kr + 56 Ba
2⋅23 He→ 24 He + 2⋅11H
+ 3⋅01 n
Fusion:
Für diese Fusion ergibt sich ein Massendefekt von
∆m = [2 3,0160299 – (4,0026036 + 2 1,00782522)]
-29
∆m = 2,2924999 10 kg. Das ergibt eine frei werdende Energie von
2
-29
8
2
-12
E = ∆m c = 2,2924999 10 kg (2,9979246 10 m/s) = 2,06 10 J = 12,9MeV
oder
3. Kinematik und Dynamik geradliniger Bewegungen
Wissen und Können
Anwendungen, Beispiele
Darstellung von Bewegungsabläufen in Diagrammen und
Gleichungen
Gleichförmige Bewegung (Beschleunigung a = 0)
Geschwindigkeit:
v =
∆s
∆t
(Ist zur Zeit t=0 der Ort s=0, erhält man
v =
s
.)
t
v ist die Steigung der Geraden im t-s-Diagramm
Der in der Zeit ∆t zurückgelegte Weg ∆s
lässt sich als Fläche unter der Kurve im
t-v-Diagramm veranschaulichen.
Gleichmäßig beschleunigte Bewegung
Wirkt auf einen Körper eine konstante beschleunigende Kraft,
so führt er eine gleichmäßig beschleunigte Bewegung aus.
Es gilt:
a =
F
(Beschleunigung a konstant, a 0)
m
Sind zur Zeit t=0 s(0) = 0 und v(0) = 0 so gelten die
a ist die Steigung der Geraden im t-v-Diagramm
Bewegungsgleichungen:
Die Geschwindigkeitsänderung ∆v
lässt sich als Fläche unter der Kurve
2
v(t) = a t; und s(t) = 1/2 a t
2
2
(Freier Fall: g = 9,81 m/s , v(t) = g t, s(t) h(t) = 1/2 g t )
im t-a-Diagramm veranschaulichen.
Beispiel: Berechnung des zurückgelegten Weges bei der
Gleichmäßig beschleunigte Bewegung mit
nebenstehenden Bewegung durch Berechnung der
Anfangsgeschwindigkeit v0 und Anfangsweg s0:
Flächen unter der Kurve im t-v-Diagramm!
2
v(t) = v0 + a t , s(t) = s0 + v0 t + 1/2 a t
∆s I = 5,0km , ∆s II = 3,75km , ∆s III = 3,0km
∆s ges = 11,75km ≈ 12km