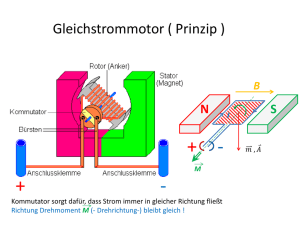
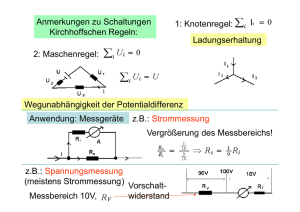
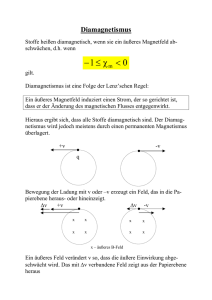
Spins Do
Werbung

13.4.2016 Spins Do -Experimenteller Magnetismus Martin Valldor Email: [email protected] IBM-Ahmed 1 Woher kommt ein magnetisches Moments wir erinnern uns... Elektrische Ladungen in Bewegung erzeugen ein Magnetfeld 2 Ein paar magnetische Definitionen Ein Stromkreis ersetzt viele kleinere Magnetisches Moment (m) m I A (Am2) 1 Am2 = 103 emu Fläche (A) Magnetisches Feld H (A/m) = m/Volumen 1000 A/ m Örstedt 4 I Magnetische Induktion B (was die Probe sieht) 104 Gauss = 1 Tesla Das magnetische Moment eines Elektrons: B = 9.274078 10-24 Am2 (J/T) Herleitung... Ladung 3 Orbitales (Bahn) Moment B Das Elektron has nicht nur eine Ladung sondern auch eine Masse Einstein-de Haas-Effekt ungeordnet geordnet l = +2 l = +1 l=0 l = -1 l = -2 Die Präzission vom Spin – Larmor frekvenz 4 Elektronische Quantenzahlen n = Prinzip-QZ l = Bahn-QZ ml = Magnet-QZ ms = Spin-QZ welche ”Schale” 0 bis (n-1) -l bis +l +½ oder –½ S = Gesamt-Spinmoment L = Gesamt-Bahnmoment J = Gesamt-Winkelmoment = S+L bis S-L Pauli-Prinzip – keine zwei Elektronen können dieselbe QZ haben Hunds-Regel: Max S, Max L, Max J Kleine Übung: Cr2+ Nd3+ Cu2+ Dy3+ 5 Zeeman-Effekt Elektronen im B-Feld E E B 0 Spektroskopie B 0 Bahnmoment (l) aufspaltung Diamagnete Gesamtmoment (j) aufspaltung Paramagnete 6 Kristallfeld hebt die Entartung auf und löscht teilweise orbitales Moment aus Energie x2-y2 3z2-r2 d-orbitale xy xz yz ohne Kristallfeld x2-y2 3z2-r2 xy xz yz 3z2-r2 Wie sieht denn pyramidal oder plankvadratisch aus? xz yz x2-y2 xy Starker Effekt für 3d-Elemente Schwächer für 4d... 5d... 4f... 5f Warum ist dieser Effekt verschwindend klein für die 4f (5f) Elemente? Was erwartet man dann bezüglich S,L und J? ”Isotropes Ion” [Eg], d5, d10, f7, f14 7 Kristallfeld-Effekte x2-y2 3z2-r2 x2-y2 3z2-r2 x2-y2 ”High spin” xy xz >”Hundsenergie” 3z2-r2 yz xy xz yz xz ”Low spin” yz xy Jahn-Teller-Effekt Was könnte der Grund für eine derart Verzerrung sein? Spin-Zustandsänderung Was ändert sich dadruch? 8 Magnetische Suszeptibilität = M/H 0> Diamagnetismus z.B. Sn, Pb, Bi 1>>0 >1 Paramagnetismus z.B. Al, Na, Ti, V Ferromagnetismus z.B. Fe, Co, Ni 9 Martin Valldor Aufbau der Vorlesung • • • • • • • • • • Diamagnetismus lokale Effekte Paramagnetismus Ferro- / Antiferro- Magnetismus globale Effekte Clustermagnetismus Spin-Dynamik Kristallstruktur-Wirkungen auf Magnetismus Magnetische Strukturen Magneto-optische Effekte Spin-Leitfähigkeit Effekte WW Effekte Quantum-Magnete - Ferroflüssigkeiten 10 Diamagnetismus Alles ist auch diamagnetisch 11 0> Diamagnetismus - Anschaulich pyrolytisches Grafit (Kohlenstoff) Metall Cu Ag Bi Elektr.Konfig. [Ar]3d104s1 [Kr]4d105s1 [Xe]4f145d106s25p3 diam. (cgs) -1.110-6 -2.410-6 -19210-6 Supermagnete http://sci-toys.com/ 12 Martin Valldor Wie erklärt man Diamagnetismus? B 3. Maxwell Gl. E B t B nach Langevin: Atom oder Ion ohne ungepaarte Elektronen Die Freiheit der Elektronen wird durch das B Feld beschränkt: Larmor präzission Das erzeugte B-Feld der Elektronen ist dem äusseren entgegengesetzt Dies gilt für all Materie mit Atomen, die eine geschlossene E-Schale haben Nach Landau: (Wir erinnern uns an Lenz Regel) Metallstück Lorenzkräfte zwingen die Elektronen in eine Kreisbewegung Das erzeugte B-Feld der Elektronen ist dem äusseren entgegengesetzt 13 Wie verhält sich ein Diamagnet M (emu) Isolator Gd-implantierte GaN Probe 1.86 K M (emu) Dünnschicht von ZnO (B||c) Diamagnetismus von Bi temperaturUNabhängiger Effekt A. Ney et al. Journal of Magnetism and Magnetic Materials 320 (2008) 3341–3346 aber Feldabhängiger Effekt, oder? 14 de Haas, W. J. and van Alphen, P. M. (I930) Commun. phys. Lab. Univ. Leiden, No. 212. Diamagnetismus - Anisotropie Abgeschlosse Elektronenschale heisst nicht isotropie Li3N Stephen Blundell, Magnetism in Condensed Matter, Oxford University Press 2001 Graphit sp2 - Hybridizierung 15 A.Maaroufi et al. J. Phys. Chem. Solids 43 (1982) 1103 Welche Probe könnte Anisotropie zeigen? Diamagnetismus berechnen Elektronenladung Bahnenradius M e2 r 2 6me magnetishe Induktion B0 M , B 0 H H Typische Zahlen: r = 0.5 Å ne = 2.7·1023 e·g-1 ergeben: = 4· 10-6 cm3·g-1 Elektronenmasse Stephen Blundell, Magnetism in Condensed Matter, Oxford University Press 2001 Avogadros Konstante dia M N 0e 2 Z eff r 2 H V 6me Molvolumen He M (10-6 cm3/mol) -1.9 ”Effektive Ladung” in der Valenzschale Ne Ar Kr -7.2 -19.4 -28.0 Xe -43.0 16 Empirischer Diamagnetismus CaBr2 LiF Ion/Atom /10-6 (emu/mol) Li = +14.2 = -4.2 Li+ F = -6.3 F= -11 LiF = -10.1 A A+ Ion/Atom /10-6 (emu/mol) Ca = +40 = -15.6 Ca2+ Br2(l) = -56.4 2Br= 2*(-36) = -73.8 CaBr2 + B = + B- = SiO2 Ion/Atom /10-6 (emu/mol) Si = -13.5 = -15.6 Si4+ = +3449 O2 2*O2= 2*(-12) = -29.6 SiO2 AB ? Es ist NICHT möglich einfach die individuellen Dia(/Para-)magneten zusammen zu rechnen. 17 10-6cgs-emu Empirischer Diamagnetismus χdiam = -4.80 -11.56n diag(H2) = -3.96 n = Anzahl von C in der Kette [X-] = [Eg] 18 Empirischer Diamagnetismus Aussagen: Senkrecht zu Aromaten ist relativ grösser Parallel zu Konjugierten Systemen ist relativ grösser ”Elektronreiche Säulen” erhöhen 19 In der Literatur - Moleküle CO(g) NO(g) H2O(g) 6* 6* 2* 2* 2p 2p 5 5 1s 2p 2s 1 1 4* 4* 2s C /10-6 3 O (emu/mol) = -9.8 2p 2p 2s 2s 2s N 3 O /10-6 (emu/mol) = +1461 2H O /10-6 (emu/mol) = -13.1 20 In der Literatur - Clusters Miessler and Tarr, Inorganic Chemistry, Prentice-Hall International 1991 Fe2+ Fe[cp]2 Cyklopentadienylionen Wie kann ich dieses Molekül magnetisch machen? Ganzzahlige Bindungordnungen bedeuten Diamagnetism 21 ”Perfekter” Diamagnetismus in Supraleitern Sn He(l) Sn Warum ist ein Supraleiter ein Diamagnet? 22 Martin Valldor ”Perfekter” Diamagnetismus in Supraleitern ”Quasipartikel” Boson 23 Martin Valldor Yanpeng Qi et al. New J. Phys. 10 (2008) 123003 J. Bardeen, L. N. Cooper, and J. R. Schrieffer, Phys. Rev. 106 (1957) 162-164, Phys. Rev. 108 (1957) 1175 Zusammenfassung - Diamagnetismus • Gepaarte Elektronen erzeugen im B-feld ein eigenes Magnetfeld was dem äusseren entgegengesetzt ist. • Schwacher Effekt • Der Effekt kann Anisotropie aufweisen • Die diamagnetische Suszeptibilität () ist bislang nicht möglich völlig vorherzusagen – nur emprische Daten stehen zur Verfügung. Nächste Woche (20.4.2016) geht es um Paramagnetismus 24 Aus der Kvantizierung der Energie me r r me (e) (e) I 2r r (e) (e)r (e) r I B 2r 2 2me 2 2 B = 9.274*10-24 [Am2] 25