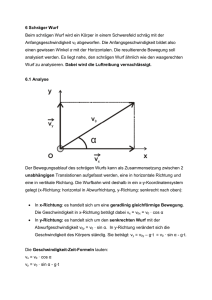
Physik_Mechanik_1A [Repariert]
Werbung
![Physik_Mechanik_1A [Repariert]](http://s1.studylibde.com/store/data/001058500_1-93d19dcf5d008d7afaee85e68da7ea91-768x994.png)
PHYSIK 1 (1) 1. Semester ET Prof. Dr. Herbert Neuendorf [email protected] Tel : 470 LO.B 1.02 Anliegen → Pointer für Vorlesungen : Elektrotechnik, Signale & Systeme … Klausur : Gesamtmodul über beide Semester Skript : Folien als pdf Übungen : Handouts www.dhbw-mosbach.de/studienangebote/wirtschaftsinformatik/kontakt/ prof-dr-neuendorf/aktuelle-lehrveranstaltungen.html → Physik_1A.pdf und folgende … Literatur : Tipler, Pysik, Oldenbourg Hering, Martin, Stohrer, Physik für Ingenieure, Springer Kuypers, Physik für Ingenieure und Naturwissenschaftler, Wiley-VCH, Bd 1 + 2 Harten, Physik, Springer von Oppen, Melchert, Physik für Ingenieure, Pearson © H.Neuendorf ☺ PHYSIK 1 (2) Prof. Dr. Herbert Neuendorf Klassische Mechanik Grundlagen Physikalische Größen, Skalare, Vektoren, Koordinatensysteme Skalarprodukt, Vektorprodukt, Differentiation, Integration Kinematik des Massenpunktes Lineare Bewegung + Kreisbewegung Differentiation des Ortsvektors, Integration des Beschleunigungsvektors Inertialsystem Dynamik Newton'sche Axiome, Schwere vs Träge Masse, Gravitation, Impuls Integration der Bewegungsgleichung, Phasenraumdarstellung Differentialgleichungen Numerische Integrationsverfahren (Euler, RK4) Erhaltungsgrößen Arbeit, Energie, Leistung Energieerhaltungssatz der Mechanik Skalares Feld, Vektorfeld - Kraftfeld als Gradient der Potentiellen Energie Exkurs : Rotation, Divergenz Massepunktsysteme, innere Kräfte, äußere Kräfte, Impulssatz Drehimpuls und Drehmoment (Kreisel) © H.Neuendorf Inhalte Mechanik … Bewegungen starrer Körper Trägheitsmomente, Berechnung für einfache Fälle Drehimpuls + Rotationsenergie Mechanische Schwingungen Ungedämpfte + gedämpfte freie Schwingungen (Lösung DGL) Erzwungende Schwingungen, Resonanz, Leistungsaufnahme Einschwingvorgänge Analogie mechanische + elektrodynamische Schwingungen Superposition von Schwingungen, Fourierreihe Wellen Beschreibung von laufenden + stehenden Wellen Harmonische Wellen, Wellengleichung, Phasengeschwindigkeit, Intensität Energietransport durch Wellen Wellengruppen (Signale), Gruppengeschwindigkeit Exkurs: Fourieranalyse + Synthese, Unschärferelation Kohärenz + Interferenz im Fernfeld Vielstrahl-Interferenz + Beugung + Gitter + Auflösungsvermögen © H.Neuendorf (3) (4) Anliegen und Verortung der Physik als Wissenschaft Physik : Grundlegendste Naturwissenschaft Eigenschaften + Wechselwirkungen der Materie ← Experiment + Theorie Verständnis aller Phänomene der unbelebten (z.T. auch belebten) Natur Ziel : Reduktion + Vereinheitlichung in Theorien, Modellen → Naturgesetze → Zusammenfassung in möglichst wenigen und grundlegenden Gesetzen - aus denen möglichst viele empirische Einzeltatsachen ableitbar sind ! Einstein : Mein eigentliches Forschungsziel war stets die Vereinfachung und Vereinheitlichung des physikalischen theoretischen Systems. Physiker sind Mathematiker mit Sinn für die Realität ….. Mathematik : Das große Ziel aller Wissenschaft ist es, die größte Anzahl empirischer Tatsachen durch logische Herleitung aus der kleinsten Anzahl von Hypothesen oder Axiomen zu erfassen Das Buch der Natur ist in der Sprache der Mathematik geschrieben (Galilei) Biologie / Medizin : Untersuchung der Vorgänge in lebenden Organismen, Untersuchung von Selbstorganisationsvorgängen Chemie : Physik Ingenieurwissenschaften : Direkte Umsetzung physikalischer Erkenntnisse: Elektronik, Systemtheorie, Mechatronik … © H.Neuendorf Untersuchung der Bildung und Umwandlung von Molekülen Einige Teilgebiete der Physik (5) Klassifikationen der Physik Hochenergiephysik → Elementarteilchen und ihre Wechselwirkungen Kernphysik → Aufbau und Eigenschaften der Kernmaterie Atom- und Molekülphysik → Eigenschaften der Atome und ihrer Verbindungen Festkörperphysik → Eigenschaften der kondensierten Materie Plasmaphysik → Eigenschaften hochionisierter Gase Astrophysik & Kosmologie → Eigenschaften und Entstehung des Universums Physik Allgemein Einige aktuelle Forschungsfelder Erweiterung des Standardmodells der Materie Kosmologie, Quantentheorie der Gravitation Bedeutung nichtlinearer Prozesse - z.B. in Optik Gibt tiefe Einblicke in die Natur und korrigiert unsere Vorstellungen von Raum, Zeit und Kausalität Konkret Grundlage der modernen Technik und Zivilisation Verständnis ungeordneter Materie (Polymere, Gläser ...) Mikromechanik, Nanophysik Halbleiterpysik, Optische Rechner, Quantum Computing … © H.Neuendorf Man studiert Mathematik, um entscheiden zu können, welche der wichtigen Aussagen richtig sind … Man studiert Physik, um entscheiden zu können, welche der richtigen Aussagen wichtig sind … (6) Klassifikationen Klassifikationen der Physik v c Relativistische Relativistische Kosmologie klassische Quantenphysik ART Physik Klassische Physik Quantenphysik "gewöhnliche Astrophysik Objekte" 0 10-15 Atomkerne © H.Neuendorf 10-7 1011 1026 L [m] Universum (7) Ziel der Physik als Wissenschaft Über bloße unverbundene Erfahrungstatsachen hinaus gehen ⇒ Verallgemeinerte Theorien zur Deutung + Vorhersage vieler Einzelerscheinungen Richtigkeit Theorie = Anwendbarkeit + Einfachheit Theorie-Klassifikation : 1. Punkttheorien Bsp Punktmechanik der Massepunkte, ausdehnungsloses Elektron Phys. Größen nur in diskreten Punkten des 3d-Raumes definiert Koordinaten sind Funktionen der Zeit ⇒ Zeit als einzige unabhängige Variable 2. Feldtheorien / Kontinuumstheorien Bsp Wellen, Elektrodynamik Phys. Größen in jedem Punkt des 3d-Raumes definiert Sind lokale Funktionen von Zeit + Ort 3. Systemtheorien ⇒ Auch Koordinaten als unabhängige Variablen Bsp Thermodynamik Makroskopische Zustandsgrößen beschreiben räumlich ausgedehnte Systeme Zustandsgleichungen verknüpfen die Zustandsgrößen (p, V, T, N) Statistische Fundierung der Zustandsgrößen Abgeschlossene Theorie Bsp: Klassische Mechanik versus RT + QM 1. Kann durch kleine Änderungen nicht mehr signifikant verbessert werden – nur durch Einführung ganz neuer Begriffe - was jedoch Übergang zu neuer Theorie bedeutet 2. Kennt die Grenzen ihrer Gültigkeit und Anwendbarkeit © H.Neuendorf (8) Induktion Physikalische Erkenntnis n → n+1 Verallgemeinerung Experiment Zusammenhänge physikalischer Größen Regelkreis physikalischer Erkenntnis Physikalisches Gesetz Naturgesetze Messvorschriften Verifikation / Test Einstein : Deduktion Grundanliegen der Pysik ist TheorieVereinheitlichung = Reduktion : Die Theorie bestimmt, was beobachtbar ist … Neue Voraussagen Vermutungen Die verschiedenen historisch entstandenen Theorien sollen auf wenige fundamentalere Theorien zurückgeführt werden. Physical laws should have mathematical beauty Dirac, 1956 Klassifikationen der Physik Makrophysik > 10-6 m Mikrophysik <≈ 10-10 m Unmittelbar wahrnehmbar Anschauliche Bilder Streng deterministisch Kontinuierliche stetige Abläufe (Teilbarkeit) Genaue Messbarkeit Mittelbar wahrnehmbar Unanschaulich, abstrakt Statistisch deterministisch Diskontinuierliche unstetige Abläufe (Quanten) Unschärferelation Klassische Physik Quantenphysik © H.Neuendorf Klassifikationen der Physik Mechanische Systeme (10) Einfache Mechanische Systeme Vielteilchen-Systeme Bsp: Pendel, Billardkugeln, Planeten Bsp: Teilchen eines Gases Wenige Teilchen bzw. Zusammenfassung der gemeinsamen Bewegung im Schwerpunkt Extrem große Teilchenzahlen N ≈ 10²³ in ungeordneter Bewegung Abbildung des Gesamtsystems durch einen Wert für Masse, Trägheitsmoment, Geschwindigkeit … Alle Teilchen bewegen sich individuell, können in ihrem Gesamtverhalten nicht durch eine gemeinsame Bahnkurve dargestellt werden ⇒ Zeitliche Entwicklung - Bahnkurve : ⇒ Zeitliche Entwicklung : Durch wenige Bewegungsgleichungen und Erhaltungssätze beschrieben + berechenbar Berechnung aller 10²³ Teilchenbahnen nicht möglich – extremer Rechenaufwand r (t) (Thermodynamik) m2 m1 Keine mikroskopischen Detail-Angaben in Vielteilchen-Systemen möglich !! ⇒ Definition makroskopischer Zustandsgrößen + Übergang zur Statistischen Physik © H.Neuendorf Messung und Maßeinheit : Physikalische Größen + Maßsysteme (11) Ausdruck physikalischer Zusammenhänge in normierten Größen : 1. Skalare Größen = ungerichtete Größen (Länge, Masse, Zeit, Energie ....) 2. Vektorielle Größen = räumlich gerichtete Größen (Geschwindigkeit, Kraft, Impuls ....) Unabhängige SI-Basisgrößen : Mechanik: Masse [kg] Länge [m] Elektriztätslehre: Stromstärke [A] Thermodynamik: Temperatur [K] Optik: Lichtstärke [cd] Zeit [s] Stoffmenge [mol] Maßsystem durch Grundgrößen + ihre Einheiten bestimmt : cgs = [cm] [g] [s] mks = [m] [kg] [s] Seit 1978 : SI-System Festlegung physikalischer Größen durch : a) Zahlenwert {G} = "Menge" b) Einheit [G] = "Norm" Skalare Größe g = {G} • [G] Geschw. = Länge / Zeit Vektorielle Größe g = {G} • [G] • e e = Einheitsvektor = g / g in Richtung von g Alle anderen Größen sind aus Grundgrößen abgeleitet : Beschl. = Geschw. / Zeit |e|=1 Kraft = Masse ·Beschl. ... © H.Neuendorf Größenordnungen Zehnerpotenzen als Faktoren für SI-Einheiten : 10 12 Tera Gebräuchliche Nicht-SI-Einheiten : Länge : 1 LJ = 9.46·10 15 m T 10 9 Giga G 10 6 Mega M 10 3 Kilo k 10 0 - - (12) Abgeleitete Größen Lichtjahr 1 Å = 10 -10 m Ångström 1 fm = 10 -15 m Fermi Masse: 1 t = 10 3 kg Tonne 1 u = 1.6604· 10 -27 kg Zeit: atomare Masseneinh. 1 min = 60 s 1 h = 3600 s 1 d = 86400 s 1 a = 365.24 d = ..... s 10 -3 milli m 10 -6 mikro µ 10 -9 nano n Wichtige abgeleitete Größen : 10 -12 piko p Frequenz → Periodische Vorgänge - Anzahl n in Zeit t femto f 10 -15 f=n/t [ Hz = s-1 ] ( ≠ Kreisfrequenz ω ! ) Ebener Winkel : r ϕ s Gradmaß → Vollkreis = 360° 1° = 60' Bogenmaß → ϕ = s / r R Ω © H.Neuendorf A 360° ≡ 2π Raumwinkel : ⇒ 1' = 60'' [ rad ] 1 rad ≡ 360°/2π = 57.295° Ω = A / R2 [ sr ] Steradiant Vektorielle Größen → → (13) → a =| a | ⋅ e a Ein Vektor ist durch Betrag und Richtung definiert Vektoraddition : a x + bx a + b = b + a = c = a y + by Vektorsubtraktion : a z + bz → → → → → → → → Betrag des Vektors → b → a → a − b = a + (− b ) Projektion eines Vektors auf Wirkungslinie eines anderen Vektors : → −b → a → b Komponentenzerlegung : → → → → Koordinatendarstellung : → → a → c b α b ax = a x ⋅ e x + a y ⋅ e y + az ⋅ ez = a y a z → ab → → a = ax+ a y+ az = → → | a b |=| a | ⋅ cos(α ) → c = a+ b → Einheitsvektor in Richtung von a → a Vektor-Betrag in cartesischen Koordinaten : → | a | = a x2 + a 2y + a z2 Einheitsvektor in Richtung von a : → a a x a y az e a = = , , a a a a → © H.Neuendorf → ea =1 Cartesische Einheitsvektoren liegen parallel zu Koordinatenachsen x, y, z : → → → ex ey ez (14) Vektorielle Größen a Skalarprodukt zweier Vektoren (Inneres Produkt) : Liefert Skalar α → → b a ⋅ b = a ⋅ b ⋅ cos(α ) → → → → → → Skalarprodukt in Komponentendarstellung KG : a ⋅ b = b ⋅ a → Durch Ausmultiplizieren in cartesischer Darstellung unter Beachtung der Sonderfälle : → → → → DG : a ⋅ ( b + c ) = a ⋅ b + a ⋅ c → → a⋅ b = → → → → ⇒ a⋅ a = a 2 → → → → → → → → → = a x ⋅ b x ⋅ e x ⋅ e x + a y ⋅ b y ⋅ e y ⋅ e y + a z ⋅ bz ⋅ e z ⋅ e z = a x ⋅ b x + a y ⋅ b y + a z ⋅ bz → → a ⊥ b ⇒ a⋅ b = 0 Physikalische Motivation : Berechnung der Arbeit bei beliebiger Orientierung von Kraft und Weg Speziell : Betrag eines Vektors → → → → → → → → → → → → e x ⋅ e y = e y ⋅ ez = e x ⋅ ez = 0 e x ⋅ e x = e y ⋅ e y = ez ⋅ ez = 1 © H.Neuendorf → → → a || b ⇒ a ⋅ b = a ⋅ b → → = (a x ⋅ e x + a y ⋅ e y + a z ⋅ e z ) ⋅ (b x ⋅ e x + b y ⋅ e y + bz ⋅ e z ) Spezialfälle : → → → → a⋅ a = a 2 = a x a x + a y a y + a z az → ⇒ | a |= a x2 + a 2y + a z2 (15) Vektorielle Größen c Vektorprodukt zweier Vektoren (Äußeres Produkt) : Liefert Vektor ! b Vektoren bilden mit resultierendem Vektor ein Rechtssystem Rechtsschraube, RechteHand-Regel : a → b → → → c = a ⋅ b ⋅ sin(α ) a× b = c → → → c ⊥ a, → c ⊥b → → → → → → → DG : a × ( b + c ) = a × b + a × c (kein KG!) → → → a Physikalische Motivation : Berechnung der Drehmoments bei beliebiger Orientierung von Kraft und Hebelarm ⇒ a× b = 0 → → → → → → → → a⊥b → → ⇒| a × b |= a ⋅ b → → e y × e x = − ez b c → e x × e y = ez → → b× a = − a× b → → a ⇒ a× a = 0 → → a×λ b = λ ⋅(a× b ) α → a || b → → → → → α Gemäß Rechtsschraubenregel → → → → e y × ez = e x → → Spezialfälle : → → → ez × e x = e y → ez × e y = − e x → → → → → e x × ez = − e y → e x × e x = e y × e y = ez × ez = 0 Geometrische Deutung : Der Betrag des Vektorprodukts ist gleich der Fläche des von den Vektoren aufgespannten Parallelogramms © H.Neuendorf Vektorprodukt in Komponentenschreibweise : Komponentendarstellung der Vektoren und Bildung der Vektorprodukte unter Beachtung der Spezialfälle parallel / senkrecht → → → → → → → → a × b = ( a x e x + a y e y + a z e z ) × ( b x e x + b y e y + bz e z ) = → → → → → → → → → Definition eines rechtshändigen Koordinatensystems : → → → → e x × e y ⋅ e z = +1 z + a y b x e y × e x + a y b y e y × e y + a y bz e y × e z + → → → → → Vektorielle Größen → = a x b x e x × e x + a x b y e x × e y + a x bz e x × e z + → y → x + a z b x e z × e x + a z b y e z × e y + a z bz e z × e z → → Determinanten-Schreibweise : → = a x b y e z + a x bz ( − e y ) + a y b x ( − e z ) + → → → → → ex a× b = ax ey ay ez az bx by bz → → → + a y bz e x + a z b x e y + a z b y ( − e x ) a y bz − a z b y = ( a y bz − a z b y ) e x + ( a z b x − a x bz ) e y + (a x b y − a y b x ) e z = a z b x − a x bz a b − a b y x x y Übung: Was erhält man speziell für zwei Vektoren a und b die in der (x,y)-Ebene liegen ? → © H.Neuendorf (16) → → Koordinatensysteme - Zusammenhang mit cartesischen Koordinaten (17) Beschreibung physikalischer Zusammenhänge in verschiedenen frei wählbaren Koordinatensystemen → Länge + Richtung von Vektoren bleibt erhalten Naturgesetze dürfen weder vom Maßsystem noch vom Koordinatensystem abhängen ! Voraussetzung : Inertialsystem = nicht-beschleunigtes System ! Auch in nichtcartesischen Systemen sind spezielle Einheitsvektoren e definiert : 1. Ebene Polarkoordinaten : r = Abstand vom Ursprung ϕ = Winkel(Verbindungsvektor, x-Achse) y e T P : r ,ϕ x = r ⋅ cos(ϕ ) y = r ⋅ sin(ϕ ) r= tan(ϕ ) = x2 + y2 er ϕ x y x r = Länge (x,y)-Ortsvektorprojektion ϕ = Winkel( Proj.Vektor, x-Achse ) © H.Neuendorf radiale + tangentiale Einheitsvektoren r e r ⊥ eT ⊥ e z 2. Zylinderkoordinaten : z = Abstand von (x,y)-Ebene P P : r ,ϕ , z Koordinatensysteme z r·sin(ϑ) r = Abstand vom Ursprung = Länge Ortsvektor P ϕ = Meridianwinkel(xy-Projektion Ortsvektor, x-Achse) ϑ ϑ = Polwinkel(Ortsvektor, z-Achse) P : r , ϕ ,ϑ ϕ = [0,2π ] x = r ⋅ sin(ϑ ) ⋅ cos(ϕ ) ϑ = [0, π ] y = r ⋅ sin(ϑ ) ⋅ sin(ϕ ) z = r ⋅ cos(ϑ ) tan (ϕ ) = © H.Neuendorf x + y +z y x r Draufsicht y ϕ x r ⋅ sin(ϑ ) ⋅ cos(ϕ ) sin(ϑ ) ⋅ cos(ϕ ) r = r ⋅ sin(ϑ ) ⋅ sin(ϕ ) = r ⋅ sin(ϑ ) ⋅ sin(ϕ ) = r ⋅ e r r ⋅ cos(ϑ ) cos(ϑ ) z 2 ϑ P Radialer (Einheits-) Vektor mittels Kugelkoordinaten : x2 + y2 + z2 cos(ϑ ) = r r·cos(ϑ) 3. Kugelkoordinaten = räumliche Polarkoordinaten : r= (18) z 2 2 sin(ϑ ) ⋅ cos(ϕ ) ⇒ e r = sin(ϑ ) ⋅ sin(ϕ ) cos(ϑ ) Sehr nützlich : sin 2 (α ) + cos 2 (α ) = 1 Koordinatensysteme Translation (19) z' Übergang zu verschobenem Koordinatensystem P z r Verschiebevektor R bewirkt parallele Translation mit Koordinaten-Transformation : r' R x' y' y x x' → → x − Rx R+ r ' = r ⇒ r ' = y' = r − R = y − R y z' z − Rz → → → → Translation : Richtung + Länge aller Vektoren erhalten ⇒ Symmetrieoperation / keine Beschleunigung Rotation : ⇒ Keine Symmetrieoperation / zusätzliche Beschleunigung Inertialsysteme : Naturgesetzliche Beschreibung ist in allen gleichförmig bewegten, unbeschleunigt translatierenden, nicht rotierenden Koordinatensystemen identisch ⇒ Alle Inertialsysteme sind physikalisch gleichwertig ! Es gibt kein ausgezeichnetes Inertialsystem ! © H.Neuendorf Symmetrie = Invarianz unter Transformation "Etwas ist symmetrisch, wenn man es einer bestimmten Operation unterziehen kann und es ist nach der Operation noch genau dasselbe" H.Weyl Kinematik der Massenpunkte Lehre von Bewegungen der Körper : Beginn der empirischen Physik mit Galilei : Experimente + Messungen, Definition neuer Begriffe, mathematische Formulierung (20) Berechnung von Bahnkurven Rein mathematischer Ansatz → Ursache der Bewegung = Kräfte werden nicht formuliert ! Modell = Idealisierung → Absehen von Ausdehnung → Körper = Punktmasse Konsequenz der Näherung : Elimination von Störeffekten → Vernachlässigung von Eigenrotation + Drehmomenten r (t ) Vernachlässigung von Verformungen + Eigenschwingungen Alle auf Körper wirkenden Kräfte greifen in einem Punkt an Zeitabhängige Position des Körpers durch nur einen Ortsvektor r(t) beschrieben geradlinig ⇒ eindimensional Geschwindigkeit : a) Gleichförmige 1d-Bewegung v := ∆x = const ∆t v= Gleiche Strecken In gleichen Zeitintervallen x ( t ) − x (0 s ) x ( t ) − x 0 = (t − 0 s) t ⇒ x (t ) = x0 + v ⋅ t Weg-Zeit-Diagramm = Gerade x Konstante Steigung ∝ konstante Geschwindigkeit v x0 Wichtig : Relativ zu welchem Bezugssystem = Inertialsystem ? © H.Neuendorf x(t) t (21) Kinematik der Massenpunkte : Geschwindigkeit b) Ungleichförmige geradlinige Bewegung : In gleichen Zeitintervallen ungleiche Strecken zurückgelegt Weg-Zeit-Diagramm ist gekrümmte Kurve Für endliche Zeitintervalle erhält man als Mittelwert die mittlere Geschwindigkeit v m := ∆x ≠ const ∆t x (t 2 ) − x (t1 ) x (t 4 ) − x ( t 3 ) ≠ (t 2 − t1 ) (t 4 − t 3 ) Mittlere Geschwindigkeit = x Tangente grobes, unzureichendes Maß x(t) Sekante zwischen zwei Zeitpunkten (zeitabhängig!) Sekante Momentane Geschwindgkeit = t Geschwindigkeit zu einem bestimmten Zeitpunkt = Steigung der Tangenten im Weg-Zeit-Diagramm t1 ∆t t2 Anstieg der x(t) -Kurve = 1. Ableitung x(t) nach Zeit x (t1 + ∆t ) − x (t1 ) dx (t ) • ∆x v (t ) := lim = lim = = x (t ) ∆t → 0 ∆t ∆t → 0 ∆t dt Voraussetzung : Stetiger Verlauf, Differenzierbarkeit © H.Neuendorf Differentialschreibweise ! Mit immer kleiner werdendem Zeitintervall ∆t geht Sekante = mittlere Geschwindigkeit in Tangente = momentane Geschwindigkeit über (22) Kinematik der Massenpunkte : Wegberechnung Bei konstanter Geschwindigkeit v = ∆ x / ∆ t = const ist Wegstrecke einfach multiplikativ : ∆x = v ⋅ ∆t Nicht-konstante Geschwindigkeit v(t) = dx(t) / dt Nur über kleine Zeitintervalle ∆t ist v ≈ konstant v(t) Näherung umso besser, je feiner Unterteilung Ziel ∆ t → 0 : Liefert Integral-Begriff ∆x = x (t e ) − x (t a ) = v (t1 ) ⋅ ∆t + v (t 2 ) ⋅ ∆t + K = = te v (t i ) ∆t = ∫ v ( t )dt ∑ ∆t → 0 ta t t1 t2 t3 t4 t5 t6 t7 ta te b) v = g·t Integration als Umkehrung der Differentiation Mit Differentialen kann man "rechnen" dx (t ) ⇒ v (t ) ⋅ dt = dx (t ) ⇒ dt Bsp: a) v = const © H.Neuendorf ∆t lim i v (t ) = ∆x3 → Aufsummation aller Teilstrecken v(t) ·∆ t v(t3) = v(ti ) → Unterteilung in kleine Zeitintervalle ∆ t ∫ v (t ) ⋅ dt = ∫ dx (t ) = ∆x Weg ist die Fläche unter der / das Zeit-Integral über die Geschwindigkeits-Zeit-Kurve. ⇒ ∆x = ∫ v dt = v ∫ dt ⇒ ∆x = ∫ v dt = ∫ g·t dt = 1/2g t2 = v·∆t Geschwindigkeit ist der Anstieg / die zeitliche Ableitung der Weg-Zeit-Kurve Differentialrechnung einer Veränderlichen (23) f(x) = y f(x2) Differenzenquotient = Sekantenanstieg ∆y Verhältnis ∆ y / ∆ x ist der Differenzenquotient ∆y f ( x 2 ) − f ( x1 ) f ( x1 + ∆x ) − f ( x1 ) = = ∆x x 2 − x1 ∆x Differentialquotient = Tangentenanstieg Grenzübergang ∆x → 0 x1 ∆x f(x1) x2 x f(x) = y "Anstieg am Punkt x0" df ( x ) ∆y dy lim = = f ' ( x0 ) = ∆x → 0 ∆x dx dx x x0 0 x Definition dient zur Berechnung von Differentialquotienten mittels Grenzwertbetrachtung : Bsp : f ( x) = 3 x 2 Aus solchen Grenzwertbetrachtungen erhält man alle bekannten symbolischen Ableitungsregeln ! f ( x + ∆x ) − f ( x ) 3( x + ∆x ) 2 − 3 x 2 ⇒ f ' ( x ) = lim = lim = ∆x → 0 ∆x → 0 ∆x ∆x 3 x 2 + 6 x ⋅ ∆x + 3∆x 2 − 3 x 2 6 x ⋅ ∆x + 3∆x 2 = lim = lim = lim (6 x + 3∆x ) = 6 ⋅ x ∆x → 0 ∆x → 0 ∆x → 0 ∆x ∆x © H.Neuendorf 1. y=a ⇒ 3. y = cx 2 ⇒ y ' = 2cx 5. y = xn ⇒ y ' = n ⋅ x n −1 6. y = u( x ) + v ( x ) ⇒ 7. y = u( x ) ⋅ v ( x ) ⇒ 8. y= 9. y' = 0 u( x ) ⇒ v( x) 10. y = ex 11. y = sin( x ) ⇒ ⇒ y = x3 y = x −n = y ' = u'+ v ' u'⋅v − u ⋅ v ' y' = y' = e x v 2 y ' = b = const ⇒ 1 xn y' = 3 x 2 ⇒ y ' = − n ⋅ x − n −1 = Ableitungsregeln −n x n +1 (Summenreg el) (Produktregel) (Quotientenregel) df du df ⋅ = du dx dx y = c ⋅ e a⋅ x ⇒ y ' = cos( x ) y = sin(ϕ (t )) ⇒ © H.Neuendorf 4. y ' = u ⋅ v '+ v ⋅ u' y' = y = f (u( x )) ⇒ y = bx ⇒ 2. (24) (Kettenregel) y ' = c ⋅ a ⋅ e a⋅ x y = cos( x ) ⇒ y ' = − sin( x ) dy dy dϕ dϕ = ⋅ = cos(ϕ (t )) ⋅ dt dϕ dt dt "Kürzen" der Differentiale (25) b ∫ f ( x )dx = a 2. ∫ f ( x )dx + ∫ f ( x )dx a b a≤m≤b m f(x) b ∫ k ⋅ f ( x )dx = k ⋅ ∫ f ( x )dx a 3. Integrale b k = const a b b a a 0 0 a ∫ f ( x )dx = ∫ f ( x ) dx −∫ f ( x ) dx = f ( xi ) 1. m − ∫ f ( x )dx b x a 4. ∫ f ( x )dx = 0 ∆x xi a a b 5. ∫ ( f ( x ) + g ( x )) dx = ∫ a a b 6. b ∫ a f ( g ( x )) dx = g (b) ∫ g (a ) b f ( x ) dx + ∫ g ( x ) dx f (g )⋅ ∆x = a dx dg dg Subst . F= Fläche unter Kurve b−a n Definition des Integrals : n lim n → ∞ , ∆x → 0 b ∑ f ( x ) ⋅ ∆x i =1 = ∫ f ( x ) dx a © H.Neuendorf b i (26) Integration : Stammfunktionen 1. Hauptsatz der Integralrechnung ∫ f ( x ) dx = 0 + c f ( x) = 0 ⇒ Differentiation kehrt Integration um ⇒ Test der Regeln durch Ableiten 2. f ( x ) = bx ⇒ 3. f ( x ) = bx 2 5. f ( x) = x n ∫ −n 6. f ( x) = x 7. f ( x ) = b ⋅ e a⋅ x ∫ f ( x ) dx = ∫ ⇒ ⇒ F = ∫ f ( x ) dx ⇒ F ' ( x ) = f ( x ) 1 f ( x ) dx = bx 3 + c 3 ∫ ⇒ ⇒ 1 2 f ( x ) dx = bx + c 2 1 ⋅ x n +1 + c n +1 1 f ( x ) dx = x − n +1 + c − n +1 ∫ b f ( x ) dx = ⋅ e a⋅ x + c a Berechnung des bestimmten Integrals : Einsetzen der Integrationsgrenzen ⇒ Integrationskonstante fällt weg b b ∫a f ( x )dx = ∫0 f ( x )dx − ∫0 f ( x )dx = F (b ) − F ( a ) b 8. f ( x ) = sin( x ) ⇒ ∫ f ( x ) dx = − cos( x ) + c 9. f ( x ) = cos( x ) ⇒ ∫ f ( x ) dx = sin( x ) + c Bei physikalischen Problemen wird Wert der Integrationskonstanten durch die physikalischen Randbedingungen festgelegt !! © H.Neuendorf a b 1 Bsp : ∫ x 2 dx = x 3 3 a a 1 1 = b3 − a 3 3 3 dx v (t ) = dt Anwendung Integration auf physikalische Begriffe v = v(t) dx = v (t ) ⋅ dt Geschwindigkeit variiert ständig ∆x3 v(t3) = v(ti) ∆F3 f(x3) = f(xi) y = f(x) Nur über kleine (infinitessimale) Zeitintervalle ∆t durch festen Wert näherbar ! x ∆x a ∆x = b−a n t b ∆t a ∆t = Fläche unter Kurve n ∆Fi = ∑ n →∞ ∆F = F (b) − F (a ) = lim f ( x i ) ⋅ ∆x ∑ n → ∞ , ∆x → 0 lim i =1 b−a n Strecke = Fläche unter Geschwindigkeits-Zeit-Kurve n ∆x i = ∑ n →∞ i =1 n v ( t i ) ⋅ ∆t ∑ n → ∞ , ∆t → 0 = ∫ f ( x ) dx lim i =1 b Analog: ∆v = ∫ a ( t ) dt © H.Neuendorf ⇒ lim ∆t → 0 ∆x = x (b) − x (a ) = lim b a Grenzübergang b i =1 n (27) a b = ∫ v ( t ) dt a (28) Kinematik der Massenpunkte : Krummlinige Bahnen Lage des Massenpunktes durch drei cartesische Koordinaten bestimmt : x(t) y(t) z(t) Zusammengefasst im Ortsvektor r → → → vom Koordinatenursprung zum Ort des Teilchens → r (t ) = x (t ) e x + y (t ) e y + z (t ) e z Trajektorie x (t ) = y (t ) z (t ) v x (t ) v (t ) = v y (t ) v (t ) z → Bewegung eines Teilchens determiniert durch : 1. Anfangsbedingungen aktueller Ort r + aktuelle Geschwinigkeit v 2. Wirkende Beschleunigungen (Kräfte) Phasenraum ( r, v ) : Komplette Koordinaten beschreiben die 6 Freiheitsgrade der Bewegung pro Teilchen : 3 Komponenten des Ortsvektors 3 Komponenten des Geschwindigkeitsvektors N Teilchen ⇒ 6N Freiheitsgrade © H.Neuendorf + Kinematik der Massenpunkte (29) Krummlinige Bahnen Geschwindigkeit v durch zeitliche Ableitung aller drei Komponenten von r ⇒ v ist dreikomponentiger Vektor im Raum z x (t ) r (t ) = y (t ) z (t ) → z(t) Vektor wird differenziert, indem man komponentenweise differenziert … P r(t) ez d x (t ) v x (t ) x (t ) dt → • d ⇒ v (t ) = v y (t ) = y (t ) = y (t ) v (t ) • dt z z (t ) d z t ( ) dt • x ( t + ∆t ) − x ( t ) 1 = lim y ( t + ∆t ) − y ( t ) ∆t → 0 ∆ t z ( t + ∆t ) − z ( t ) © H.Neuendorf y(t) ey ex y x(t) x → | v |= v x2 + v 2y + v z2 = 2 2 dx dy dz = + + dt dt dt 2 Kinematik der Massenpunkte (30) Krummlinige Bahnen Bewegung des Massenpunktes entlang Bahnkurve durch zeitabhängigen Ortsvektor r(t) beschrieben, der der Bahnkurve folgt Zwischen zwei Zeitpunkten hat sich Massepunkt um Verschiebungsvektor ∆ r weiterbewegt. z Bahnkurve r(t) Auf Bahnkurve wurde Weg ∆ s durchlaufen z → → r(t) → ∆ r = r ( t + ∆t ) − r ( t ) r (t + ∆t) in (x,y)Ebene … ∆r ∆r ∆s r (t + ∆t) Für ∆t → 0 geht ∆ r → ∆ s y ∆s r(t) x y → → → v ⊥r x Kreisbewegung : Momentaner Geschwindigkeitsvektor steht stets senkrecht zum Ortsvektor ! Richtungen durch radiale und tangentiale Einheitsvektoren beschrieben © H.Neuendorf → er → r = r⋅er → → v = v⋅ eT → → r → eT v Kinematik der Massenpunkte : Beschleunigung (31) [ m / s 2] Beschleunigung a (acceleratio ) = Geschwindigkeits-Änderung durch : a) Zunahme / Abnahme Geschwindigkeitsbetrag |v| ohne Richtungsänderung → geradlinige beschleunigte Bewegung b) Richtungsänderung des Vektors v trotz konstantem Geschwindigkeitsbetrag → z.B. Kreisbewegung ! v Tangente → a) Analog Geschwindigkeit : Mittlere Beschleunigung = Sekantensteigung v(t) Momentane Beschleunigung = Tangentensteigung Sekante Zeitintervalle ∆t → 0 a m := v 2 − v1 ∆v = t 2 − t1 ∆t m s 2 v (t + ∆t ) − v (t ) d a (t ) := lim = v (t ) ∆t → 0 ∆t dt d d d 2 x ( t ) •• = x (t ) = = x (t ) 2 dt dt dt © H.Neuendorf t 3d-Vektor ! t1 t2 Geschwindigkeits-Zeit-Diagramm Erste Ableitung der Geschwindigkeit nach Zeit Zweite Ableitung der Ortsfunktion nach der Zeit Newton : Jede Beschleunigung resultiert aus Krafteinwirkung. Kräfte sind Ursache aller Beschleunigungen und somit aller Bewegungszustands-Änderungen ! Kinematik der Massenpunkte (32) Spezialfall : a(t) = const Geschwindigkeit v verändert sich linear im Geschwindigkeits-Zeit-Diagramm Änderung der Geschwindigkeit v(t) ist Beschleunigung a(t) Anfangs- / Rand-Bedingungen : Zur Zeit t = 0s hat v(t) Wert v(t=0) = v0 Festlegung Integrationskonstanten durch Anfangsbedingungen für Startzeitpunkt Zur Zeit t = 0s hat x(t) Wert x(t=0) = x0 t = t0 = 0s x (t ) = ∫ v (t ) dt = = ∫ (a ⋅ t + v 0 ) dt = a ∫ t dt + ∫ v 0 dt = 1 = a ⋅ t 2 + v 0 ⋅ t + x0 2 v v(t) = v0 + a·t v0 = v ( t = 0 ) v (t ) = ∫ a (t ) dt = a ⋅ ∫ dt = a ⋅ t + v 0 v(t) t t1 Manchmal ist die Integration trivial (wie hier), manchmal analytisch nicht mehr möglich und nur noch als Computersimulation numerisch machbar Bsp: Drei-Körper-Problem i.A. nicht mehr analytisch lösbar © H.Neuendorf t2 (33) Beschleunigung, Geschwindigkeit, Ort Entwicklung von Geschwindigkeit und Ort bei konstanter Beschleunigung : Beschl.-Zeit-Diagramm a ⇒ Geschw.-Zeit-Diagramm Orts-Zeit-Diagramm x v a = const ⇒ a>0 a>0 a>0 x0 v0 v(t) = v0 + a·t v = a ⋅t x= a 2 ⋅t 2 x(t) = x0 + v0 ·t + ½ a·t2 v0 = 0 m/s : ⇒ v2 = 2⋅a ⋅ x Durch Galilei empirisch gefunden. Eigentlich "triviale" mathematische Anwendung des Newton'schen Differentialkalküls ! © H.Neuendorf t a<0 a<0 Spezialfall x0 = 0 m a<0 t t Freier Fall Richtung Erdmittelpunkt mit breitenabhängiger Beschleunigung g = 9.81 m/s2 liefert Fallgesetze : s=½gt2 v = g·t ⇒ v 2 = 2·g·s (34) Bsp : Einfache Kinematik-Aufgabenstellung → Bremsvorgang Konstante Beschleunigung a < 0 m/s2 bei Abbremsvorgang Randbedingungen : t = 0s → v(t=0s) = v0 t = T → v( t=T ) = 0 m/s x(t=0s) = 0m v (t ) = v 0 + a ⋅ t x( t=T ) = s t=T 0 x=s Objekt steht ! Bremsweg ! a x (t ) = v 0 ⋅ t + t 2 2 m ⇒ v (T ) = 0 = v 0 + a ⋅ T s 0 1. Aufstellen bekannter Beziehungen 2. Einbau der Randbedingungen 3. Auflösen nach gesuchter Größe v ⇒ T =− 0 a 2 v 02 v 02 v 02 a 2 v0 a v0 ⇒ x (T ) = s = v 0 ⋅ T + T = v 0 ⋅ − + ⋅ − = − + =− 2 a 2a 2a a 2 a v 02 ⇒ s=− 2a © H.Neuendorf v 02 ⇔ a=− 2s ⇒ T= 2s v0 Bremsweg wächst quadratisch mit Geschwindigkeit ! (35) Kinematik der Massenpunkte Ziel der Kinematik : Integration der Bewegungsgleichungen Bestimmen der expliziten Bahnkurve r (t) Anfangsbedingungen : Festlegung Integrationskonstanten durch Anfangsbedingungen für Startzeitpunkt Zur Zeit t = 0s hat v(t) Wert v(t=0) = v0 Zur Zeit t = 0s hat x(t) Wert x(t=0) = x0 t = t0 = 0s v (t ) = ∫ a (t ) dt x ( t ) = ∫ v (t ) dt r(t) d dt v(t) ∫....dt d dt a(t) ∫....dt Der Weg von r(t) zu a(t) ist leichter und gelingt immer. Der Weg von a(t) zu r(t) ist schwieriger und nicht immer analytisch möglich. © H.Neuendorf (39) Beschleunigung durch Richtungsänderung : Kreisbewegung Massenpunkt läuft auf Kreisbahn mit Radius r = const um Ursprung Winkel ϕ(t) zwischen Achse und Ortsvektor r variiert Völlig analog zur Geschwindigkeit v 1. Gleichförmige Kreisbewegung In gleichen Zeitintervallen ∆t werden gleiche Winkel ∆ ϕ überstrichen Vom Fahrstrahl überstrichener Winkel ϕ(t) wächst linear in der Zeit ⇒ Analog zu Bahngeschwindigkeit v = ∆x / ∆t wird Winkelgeschwindigkeit definiert : ∆ϕ ϕ (t + ∆t ) − ϕ (t ) = ω := ∆t ∆t " rad " s y P r ϕ ω = const ⇒ ϕ (t + ∆t ) = ω ⋅ ∆t + ϕ (t ) t = 0 s : ϕ (0 s ) = 0 rad ⇒ ϕ (t ) = ω ⋅ t © H.Neuendorf x (40) Beschleunigung durch Richtungsänderung : Kreisbewegung ∆ϕ / ∆t ≠ const 2. Ungleichförmige Kreisbewegung Momentane Winkelgeschwindigkeit ω(t) (∆t → 0s) ⇒ Erste zeitliche Ableitung der Winkelfunktion ϕ(t) y P ω (t ) = lim ϕ (t + ∆t ) − ϕ (t ) ∆t → 0 ∆t dϕ ( t ) = dt r ∆s ∆ϕ x Drehwinkel ϕ( t ) durch Integration von ω( t ) ⇒ ϕ (t ) = ∫ ω (t ) dt Anfangsbedingung : ϕ( t=0s ) Bahngeschwindigkeit v folgt aus ω gemäß Winkeldefinition im Bogenmaß : r ⋅ ∆ϕ ∆s = lim = r ⋅ ω (t ) ∆t → 0 ∆ t ∆t → 0 ∆ t ∆ϕ = ∆s r ⇒ ∆s = r ⋅ ∆ ϕ v (t ) = lim v (t ) = r ⋅ ω (t ) © H.Neuendorf Allgemeiner Zusammenhang Gilt für gleichförmige und ungleichförmige Kreisbewegung Winkel müssen im Bogenmaß angegeben werden ! (41) Kreisbewegung Geschwindigkeiten sind Vektoren ⇒ Richtungsdefinitionen nötig 0 ω (t ) = 0 ω (t ) a) v(t) verläuft tangential zur Bahnkurve → z b) Richtung von ω(t) Senkrecht auf Bahnebene ω(t) Parallel zur Drehachse Rechtsschraubenrichtung – RechteHandRegel Beträge : v (t ) = r ⋅ ω (t ) Orientierungen : → → → v ⊥ r ⊥ω Können wir dies auch analytisch darstellen ? … ϕ y r(t) v(t) x Kreisfrequenz ω = "2π / Zeit" Rotationsfrequenz f = "Zahl Umläufe / Zeit" dϕ 2π = = 2π ⋅ f ω= dt T Periode T = Umlaufzeit = 1 / f = 2 π/ ω ω = 2π ⋅ f © H.Neuendorf ⇒ ω≠ f Gleichförmige Kreisbewegung (42) (in x,y-Ebene) y Speziell : ω(t) = const = ω dϕ ( t ) =ω dt ⇒ ϕ (t ) = ω ⋅ t r·sin(ϕ) ω (t ) = ϕ Ortsvektor r(t) der Kreisbewegung in (x,y)-Ebene : r·cos(ϕ) x x (t ) r ⋅ cos(ω ⋅ t ) cos(ω ⋅ t ) r (t ) = y (t ) = r ⋅ sin(ω ⋅ t ) = r ⋅ sin(ω ⋅ t ) z (t ) 0m 0 → Betrag von r ist konstant ! Kettenregel ! − r ⋅ ω ⋅ sin(ω ⋅ t ) − sin(ω ⋅ t ) → d r (t ) ⇒ v (t ) = = r ⋅ ω ⋅ cos(ω ⋅ t ) = r ⋅ ω ⋅ cos(ω ⋅ t ) dt 0m / s 0 → Winkelgeschwindigkeit ω ist konstant ! Betrag Bahngeschwindigkeit v ist konstant ! → eT → → v ⋅ r = r 2 ⋅ ω ⋅ (− cos(ω ⋅ t ) ⋅ sin (ω ⋅ t ) + sin (ω ⋅ t ) ⋅ cos(ω ⋅ t )) = 0 ⇒ © H.Neuendorf → → v⊥r Ortsvektor r(t) und Bahngeschwindigkeit v(t) stehen stets senkrecht zueinander ! → v (t ) = r ⋅ ω Gleichförmige Kreisbewegung Berechnung Beschleunigungsvektor a( t ) : (43) y Betrag von r konstant ! − sin(ω ⋅ t ) → d r (t ) v (t ) = = r ⋅ ω ⋅ cos(ω ⋅ t ) dt 0 → Anwendung Kettenregel ! ϕ Betrag Zentripetalbeschleunigung a(t) konstant r·sin(ϕ) Winkelgeschwindigkeit ω konstant ! r·cos(ϕ) − ω ⋅ cos(ω ⋅ t ) − cos(ω ⋅ t ) d v (t ) 2 ⇒ a (t ) = = r ⋅ ω ⋅ − ω ⋅ sin(ω ⋅ t ) = r ⋅ ω ⋅ − sin(ω ⋅ t ) dt 0 s −1 0 → → → − er → a (t ) = r ⋅ ω 2 → → v ⋅ a = r 2 ⋅ ω 3 ⋅ (sin (ω ⋅ t ) ⋅ cos(ω ⋅ t ) − cos(ω ⋅ t ) ⋅ sin (ω ⋅ t )) = 0 ⇒ → → v ⊥a Beschleunigungsvektor a(t) stets senkrecht zur Bahngeschwindigkeit v(t) a(t) stets antiparallel zum Ortsvektor r(t) a(t) zeigt stets zum Zentrum der Kreisbewegung ⇒ © H.Neuendorf Zentripetalbeschleunigung x Gleichförmige Kreisbewegung a b − azby → → y z a × b = a z b x − a x bz a x b y − a y bx Vektorielle Zusammenhänge mit Vektorprodukt 0 r ⋅ cos(ω ⋅ t ) − ω ⋅ r ⋅ sin (ω ⋅ t ) v ( t ) = ω × r (t ) = 0 × r ⋅ sin (ω ⋅ t ) = ω ⋅ r ⋅ cos(ω ⋅ t ) ω 0m 0m/s → → → Für ω(t) = ω = const Vektor a(t) zeigt immer zum Rotations-Zentrum = Zentripetalbeschleunigung Berechnung Beschleunigungsvektor : → → → ⇒ a (t ) ⊥ ω ⇒ → → z → ω(t) a (t ) ⊥ v (t ) a (t ) = ω ⋅ v = ω 2 ⋅ r → ϕ → v (t ) = ω (t ) × r (t ) Gilt allgemein - auch für ungleichförmige Kreisbewegung mit ω(t) ≠ const! © H.Neuendorf → → → Bem : → → d v (t ) d d r (t ) → → ⇒ a (t ) = = ω × r (t ) = ω × = ω × v (t ) dt dt dt → (44) y r(t) x v(t) Ungleichförmige Kreisbewegung Winkelgeschwindigkeit ω( t ) ist nicht konstant ! (45) Betrag von r ist konstant ! y ω (t ) = dϕ ( t ) ≠ const ⇒ ϕ (t ) ≠ ω ⋅ t dt ϕ r·sin(ϕ) Drehwinkel ϕ( t ) ist beliebige Funktion der Zeit ! r·cos(ϕ) x Ortsvektor r(t) der Kreisbewegung in (x,y)-Ebene : x ( t ) r ⋅ cos ϕ (t ) cos ϕ (t ) r (t ) = y (t ) = r ⋅ sin ϕ ( t ) = r ⋅ sin ϕ (t ) z ( t ) 0m 0 → Anwendung Kettenregel ! dϕ ( t ) − r ⋅ ⋅ sin ϕ ( t ) dt → − sin ϕ (t ) → d r ( t ) dϕ ( t ) ⇒ v (t ) = = r⋅ ⋅ cos ϕ (t ) = r ⋅ ω ( t ) ⋅ cos ϕ ( t ) dt dt − 1 0 0m / s → eT → → v ⋅ r = r ⋅ ω (t ) ⋅ (− cos ϕ (t ) ⋅ sin ϕ (t ) + sin ϕ (t ) ⋅ cos ϕ (t )) = 0 ⇒ © H.Neuendorf 2 Ortsvektor r(t) und Bahngeschwindigkeit v(t) stehen stets senkrecht zueinander ! → → v⊥r (46) Radiale und Tangentiale 2d-Einheitsvektoren y Ortsvektor mit radialem Einheitsvektor e r dargestellt : → r·sin(ϕ) r x (t ) r ⋅ cos ϕ (t ) cos ϕ (t ) r (t ) = = = r ⋅ = r⋅er y ( t ) r ⋅ sin ϕ ( t ) sin ϕ (t ) → ϕ x r·cos(ϕ) → | e r |= (cos ϕ (t )) 2 + (sin ϕ (t )) 2 = 1 ϕ = 0: ϕ =π : → 1 er = 0 ϕ= − 1 er = 0 → π 2 → : 0 er = 1 3π : ϕ= 2 → 0 er = − 1 cos ϕ (t ) er = sin ϕ (t ) → → Zu e r senkrechter Einheitsvektor = Tangentialer Einheitsvektor e T eT − sin ϕ ( t ) = cos ( t ) ϕ → → → → → → → eT⋅ er =0 ⇒ eT ⊥ er e T ⋅ e r = (− sin ϕ (t ) ⋅ cos ϕ ( t ) + cos ϕ (t ) ⋅ sin ϕ (t ) ) = 0 © H.Neuendorf → er eT Kreisbewegung : Allgemeine Beschleunigungen (47) Zeitliche Ableitung des Geschwindigkeitsvektors v(t) liefert Beschleunigung a(t) Komponentenweise Vektordifferentiation von v(t) : Nur noch Betrag von r sei konstant − sin ϕ (t ) d d a (t ) = v (t ) = r ⋅ ω ( t ) ⋅ cos ϕ ( t ) = dt dt 0 → → − sin ϕ (t ) − cos ϕ (t ) 2 = r ⋅ ω (t ) ⋅ cos ϕ (t ) + r ⋅ ω (t ) ⋅ − sin ϕ ( t ) = 0 0 • • → → = r ⋅ ω (t ) ⋅ e T + r ⋅ ω (t ) ⋅ (− e r ) Parallel zu v (tang.) → 2 Parallel zu -r (radial) → a (t ) = −ω ( t ) ⋅ r (t ) © H.Neuendorf 2 1.Term : Tangentiale Beschleunigung bei Änderung von ω ⇒ Verschwindet bei gleichförmiger Kreisbewegung ! 2. Term : Zentripetalbeschleunigung - zeigt zum Mittelpunkt ! Stets ≠ 0, auch wenn ω = const ! Ursache der Kreisbewegung ! Gleichf. Rotation: |a| = ω2·r = v2 / r = ω·v Übung : Wenn ω konstant ist, aber r nicht ? … Grundgrößen der Kinematik → → x, r ϕ → → dr v= dt → ω= dϕ dt → → 2 → dv d r a= = 2 dt dt → α= → Grundgrößen und ihre momentanen Änderungen → dω d ϕ = 2 dt dt a = const ⇒ v (t ) = v 0 + a ⋅ t 2 ⇒ a x (t ) = x 0 + v 0 ⋅ t + t 2 2 α = const ⇒ ω (t ) = ω 0 + α ⋅ t ⇒ ϕ ( t ) = ϕ 0 + ω 0 ⋅ t + x (t ) cos ϕ ( t ) r ( t ) = y (t ) = r ⋅ sin ϕ (t ) z (t ) 0 → v v = ω ⋅r ⇔ ω = r (51) " Galilei " → → → v = ω× r v2 = ω2 ⋅r ap = r α 2 t2 Grundsätzliche Analogie zwischen geradliniger und kreisförmiger Bewegung Entwicklung der Grundgrößen bei konstanter Beschleunigung Spezialfall Kreisbewegung : a) Vektorielle Abhängigkeiten b) Betrags-Abhängigkeiten Bislang nur mathematisch-geometrische Zusammenhänge analysiert. Noch nichts über Ursachen der Bewegungsänderungen ausgesagt. Es fehlt noch ein analytischer Kraft-Begriff - von Massen, Kräften, Energien war noch nicht die Rede ! … © H.Neuendorf Superpositionsprinzip - Unabhängige Überlagerung von Bewegungen Körper kann mehrere Teil-Bewegungen gleichzeitig ausführen Überlagern sich störungsfrei : Jede Teilbewegung läuft ab, als wäre sie allein vorhanden ⇒ Vektorielle Addition der Vektoren r(t) v(t) a(t) aller Teilbewegungen Waagerechter Wurf Horizontaler Wasserstrahl zeigt Parabelform ! Gleichförmige Bewegung in x-Richtung + freier beschleunigter Fall in y-Richtung ⇒ Wurfparabel : x = v0 ⋅ t ⇒ g 2 y = ⋅t 2 v0 ⋅ t r =g 2 ⇒ ⋅t 2 → ⇒ v0 v = ⇒ v = v 02 + g 2 t 2 g⋅t → 0 ⇒ a = g → Die frei fallende und die horizontal abgeschossene Kugel sind stets auf gleicher Höhe - und schlagen gleichzeitig auf © H.Neuendorf g y = 2 ⋅ x2 2v 0 (52) Galilei-Transformation z' Beschreibung in verschiedenen Inertialsystemen : Geradlinig gleichförmige Translation der beiden Bezugssysteme mit konstanter Geschwindigkeit V Keine Rotation (53) S( x',y',z' ) S( x,y,z ) P z r' r Keine Beschleunigung R → → → R+ r ' = r → ⇒ → → r' = r −V ⋅ t t'= t → → → r' = r − R → R(t ) = V ⋅ t v' = → → → Grundannahme klassische Physik Galileisches Relativitätsprinzip → d d dv → a' = v ' = ( v − V ) = =a dt dt dt © H.Neuendorf → → x In beiden Inertialsystemen werden gleiche Zeitintervalle gemessen - das Resultat von Zeitmessungen ist unabhängig vom Bewegungszustand des Beoabchters Durch spezielle Relativitätstheorie widerlegt ! Galilei-Transformation nur Näherung ! Gültigkeitsbereich : → → d ( r −V ⋅ t) = v −V dt → y x' Transformation Wegen V = const ist Beschleunigung a invariant gegenüber geradlinig gleichförmiger Bewegung des Bezugssystems : → y' → V << c In beiden Inertialsystemen werden gleiche Kräfte registriert In beiden Inertialsystemen herrscht die gleiche Physik Gleiche Naturphänomene, gleiche Naturgesetze, identische Gleichungen (54) Trägheitskräfte in beschleunigten Bezugssystemen Bewegungsgleichung F = m·a gilt in allen Inertialsystemen : Invarianz der Newtonschen Gleichung bei Galilei-Transformation Beschleunigung + Rotation sind keine Symmetrieoperationen für Naturgesetze ! Beschleunigtes Bezugssystem : Scheinkräfte = Trägheitskräfte S' S 2 → m a' 1 m Physikalische Situation in S und S' ist nicht äquivalent ! 2 → 1 A Beobachter in S beschreibt 2 : Beobachter in S' beschreibt 2 : Wagen 1 unter 2 beschleunigt mit A Wagen 2 gegen Beobachter in S' Wagen 2 bleibt in Ruhe mit a2' beschleunigt a2 = 0 m/s2 ⇒ F2 = 0 N ⇒ F2' = m·a2' ≠ 0 N Vergleich S mit S' : Objekt in S' fällt nicht senkrecht sondern wird zusätzlich rückwärts beschleunigt durch Trägheitskraft = Scheinkraft Die beiden Beobachter messen nicht gleiche Beschleunigungen und Kräfte – sie erhalten nicht dieselben Naturgesetze ! a' = - A Trägheitskraft m·a' im beschleunigten Bezugssystem S' ! Wahre Kräfte → Sind die Ursache von Beschleunigungen / Bewegungsänderungen Schein- / Trägheitskräfte → Werden erst durch Beschleunigungen verursacht ! © H.Neuendorf Inertialsystem – weitere Definitionen Solche Bezugssysteme, in denen ein Körper in Ruhe oder gleichförmiger Bewegung verharrt, solange keine physikalischen Kräfte auf ihn einwirken, heißen Inertialsysteme. Es ist unmöglich, in der Mechanik ein Experiment anzugeben, durch das ein Inertialsystem vor einem anderen ausgezeichnet würde. Wird eine physikalische Kraft in zwei Inertialsystemen gemessen, dann stimmen die beiden Messwerte überein. In Bezug auf alle Inertialsysteme werden dieselben Kräfte gemessen. Die Newtonschen Grundgesetze der Mechanik nehmen in der klassischen Raum-Zeit einheitlich für alle Inertialsysteme dieselbe Form an. Jede Bewegung, die in einem Inertialsystem möglich ist, gibt es auch in jedem anderen Inertialsystem. © H.Neuendorf (55) (56) Struktur von Raum und Zeit Voraussetzungen jeder universellen Physik Sind die Naturkonstanten wirklich zeitlich konstant ?? 1. Homogenität der Zeit Naturgesetze gelten zu allen Zeiten in gleicher Weise Speziell Newton: Zeit verläuft kontinuierlich und für alle Beobachter unabhängig von ihrem Bewegungszustand in gleicher Weise 2. Homogenität des Raumes Eigenschaften eines abgeschlossenen Systems hängen nicht von dessen Ort im Raum ab Naturgesetze sind invariant unter räumlicher Translation im unendlich ausgedehnten Raum An allen Orten im Universum gelten dieselben universellen Naturgesetze Speziell Newton: Absoluter 3d-Raum ist euklidisch - unabhängig von Masseverteilung "Die absolute, wahre und mathematische Zeit verfließt an sich und vermöge ihrer Natur gleichförmig, und ohne Beziehung auf irgend einen äußeren Gegenstand ... Der absolute Raum bleibt vermöge seiner Natur und ohne Beziehung auf einen äußeren Gegenstand, stets gleich und unbeweglich." 3. Isotropie des Raumes Keine Richtung im Raum ist naturgesetzlich ausgezeichnet Korrektur von Newton erst durch Einstein : 1. An Stelle der absoluten Zeit tritt die in allen Inertialsystemen konstante Lichtgeschwindigkeit. 4. Voraussetzung jeder empirischen Naturwissenschaft 2. Massen krümmen die Raumzeit lokal. Induktionsgesetz → Empirischer Schluss vom Einzelfall auf alle möglichen Fälle Logisch problematisch - aber einzige Möglichkeit, sich in der Welt zu orientieren ! © H.Neuendorf