10 Das Riemannsche Integral

10 Das Riemannsche Integral
10
50
Das Riemannsche Integral
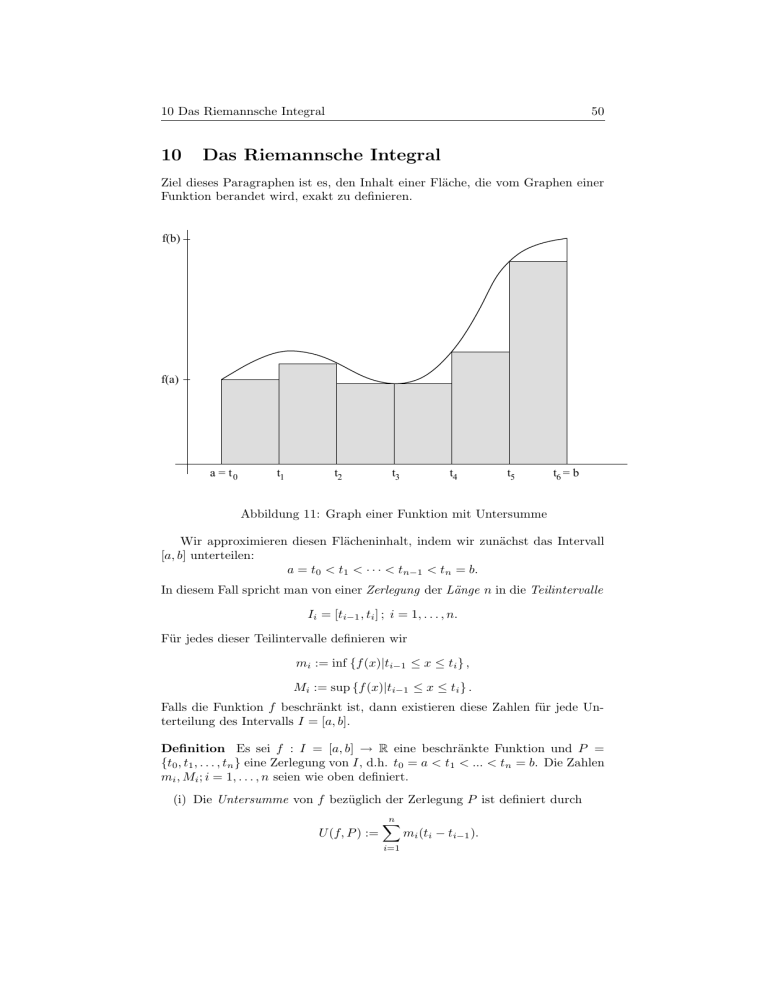
Ziel dieses Paragraphen ist es, den Inhalt einer Fläche, die vom Graphen einer
Funktion berandet wird, exakt zu definieren.
f(b)
f(a)
a = t0
t1
t2
t3
t4
t5
t6 = b
Abbildung 11: Graph einer Funktion mit Untersumme
Wir approximieren diesen Flächeninhalt, indem wir zunächst das Intervall
[a, b] unterteilen:
a = t0 < t1 < · · · < tn−1 < tn = b.
In diesem Fall spricht man von einer Zerlegung der Länge n in die Teilintervalle
Ii = [ti−1 , ti ] ; i = 1, . . . , n.
Für jedes dieser Teilintervalle definieren wir
mi := inf {f (x)|ti−1 ≤ x ≤ ti } ,
Mi := sup {f (x)|ti−1 ≤ x ≤ ti } .
Falls die Funktion f beschränkt ist, dann existieren diese Zahlen für jede Unterteilung des Intervalls I = [a, b].
Definition Es sei f : I = [a, b] → R eine beschränkte Funktion und P =
{t0 , t1 , . . . , tn } eine Zerlegung von I, d.h. t0 = a < t1 < ... < tn = b. Die Zahlen
mi , Mi ; i = 1, . . . , n seien wie oben definiert.
(i) Die Untersumme von f bezüglich der Zerlegung P ist definiert durch
U (f, P ) :=
n
X
i=1
mi (ti − ti−1 ).
10 Das Riemannsche Integral
51
(ii) Die Obersumme von f bezüglich der Zerlegung P ist definiert durch
O(f, P ) :=
n
X
Mi (ti − ti−1 ).
i=1
Unmittelbar aus der Definition folgt, dass stets gilt
U (f, P ) ≤ O(f, P ).
Wir vergleichen nun, was passiert, wenn wir verschiedene Zerlegungen betrachten.
Definition Wir sagen, dass eine Zerlegung Q = {t00 , . . . , t0m } eine Verfeinerung
der Zerlegung P = {t0 , . . . , tn } ist, falls P ⊂ Q gilt.
Satz 10.1 Es sei Q eine Verfeinerung von P . Dann gilt
U (f, P ) ≤ U (f, Q) ≤ O(f, Q) ≤ O(f, P ).
Beweis. Wir haben bereits bewiesen, dass die zweite Ungleichung gilt. Wir
werden hier die erste Ungleichung zeigen, die dritte geht analog. Ferner genügt
es, die Situation zu betrachten, wo
P = {t0 , . . . , tn } , Q = {t0 , . . . , tk−1 , u, tk , . . . , tn }
mit
a = t0 < t1 < · · · < tk−1 < u < tk < · · · < tn = b.
Es sei
m0 := inf {f (x)| tk−1 ≤ x ≤ u}
m00 := inf {f (x)| u ≤ x ≤ tk } .
Es gilt dann
U (f, P ) =
n
X
mi (ti − ti−1 ).
i=1
U (f, Q) =
k−1
X
mi (ti − ti−1 ) + m0 (u − tk−1 ) + m00 (tk − u) +
i=1
n
X
mi (ti − ti−1 ).
i=k+1
Vergleichen wir die beiden Summen, so sehen wir, dass wir die folgende Ungleichung beweisen müssen:
mk (tk − tk−1 ) ≤ m0 (u − tk−1 ) + m00 (tk − u).
Nun gilt nach Definition der Größen mk , m0 und m00 :
mk ≤ m0 , mk ≤ m00 .
Damit gilt
mk (tk − tk−1 ) = mk (u − tk−1 ) + mk (tk − u) ≤ m0 (u − tk−1 ) + m00 (tk − u).
2
10 Das Riemannsche Integral
52
Satz 10.2 Es sei f : I = [a, b] → R eine beschränkte Funktion. Dann gilt für
zwei beliebige Zerlegungen P1 und P2 von I, dass
U (f, P1 ) ≤ O(f, P2 ).
Beweis. Es sei P = P1 ∪ P2 die gemeinsame Verfeinerung von P1 und P2 . Dann
gilt nach Satz 10.1
U (f, P1 ) ≤ U (f, P ) ≤ O(f, P ) ≤ O(f, P2 ).
2
Wir betrachten nun die Mengen
U := {U (f, P )| P ist Zerlegung von [a, b]} ,
O := {O(f, P )| P ist Zerlegung von [a, b]} .
Nach Satz 10.2 ist die Menge U nach oben und die Menge O nach unten
beschränkt. Daher besitzt U ein Supremum und O ein Infimum.
Definition Es sei f : I = [a, b] → R eine beschränkte Funktion.
(i) Das Unterintegral von f auf dem Intervall I ist definiert durch
U
Zb
f (x)dx = sup {U (f, P )|P ist Zerlegung von f } .
a
(ii) Das Oberintegral von f auf dem Intervall I ist definiert durch
O
Zb
f (x)dx = inf {O(f, P )|P ist Zerlegung von f } .
a
Aus Satz 10.2 folgt sofort, dass
U
Z
b
f (x)dx ≤ O
a
Z
b
f (x)dx.
a
Definition Eine beschränkte Funktion f : I = [a, b] → R heißt auf dem
Intervall I (Riemann) integrierbar, falls gilt:
U
Z
b
f (x)dx = O
a
Schreibweise: Man schreibt:
Z
Z b
Z
f (x)dx := f (x)dx := U
a
I
Z
b
f (x)dx.
a
b
f (x)dx = O
a
Z
b
f (x)dx.
a
10 Das Riemannsche Integral
53
2
1
1
2
Abbildung 12: Die Funktion f aus Beispiel 10.1
Beispiel 10.1 Es sei I = [0, 2] und
1
f (x) :=
2
für
für
0≤x<1
1 ≤ x ≤ 2.
Für jede Zerlegung P , die den Punkt 1 enthält, gilt
U (f, P ) = 1 + 2 = 3 = O(f, P ).
Also ist f integrierbar und es gilt
Z 2
f (x)dx = 3.
0
Beispiel 10.2 Es sei I = [0, 1] und
0
f (x) =
1
für
für
x∈Q
x ∈ R \ Q.
Dann gilt für jede Zerlegung P von [0, 1]:
U (f, P ) =
n
X
0 · (ti − ti−1 ) = 0,
n
X
1 · (ti − ti−1 ) = 1.
i=0
O(f, P ) =
i=0
Also gilt
0=U
Z1
f (x)dx < O
Z
1
f (x)dx = 1
0
0
und die Funktion f ist nicht integrierbar.
Satz 10.3 Es sei a < c < b. Dann ist eine beschränkte Funktion f genau dann
auf dem Intervall [a, b] integrierbar, wenn sie auf [a, c] und [c, b] integrierbar ist.
In diesem Fall gilt
Zb
a
f (x)dx =
Zc
a
f (x)dx +
Zb
c
f (x)dx.
10 Das Riemannsche Integral
54
Beweis. Man betrachte die Partitionen von [a, b], die den Punkt c enthalten. 2
Satz 10.4 Falls f und g auf I = [a, b] integrierbar sind, dann ist auch f + g
auf I = [a, b] integrierbar, und es gilt
Zb
(f + g)(x)dx =
a
Zb
f (x)dx +
a
Zb
g(x).
a
Beweis. Es sei P = {t0 , . . . , tn } eine Zerlegung von [a, b]. Wir definieren
m0i := inf {f (x)| ti−1 ≤ x ≤ ti } ,
m00i := inf {g(x)| ti−1 ≤ x ≤ ti } ,
mi := inf {f (x) + g(x)| ti−1 ≤ x ≤ ti }
und analog
Mi0 , Mi00
und Mi . Dann gilt
mi ≥ m0i + m00i , Mi ≤ Mi0 + Mi00 .
Damit gilt für jede Zerlegung P :
U (f, P ) + U (g, P ) ≤ U (f + g, P ) ≤ O(f + g, P ) ≤ O(f, P ) + O(g, P ).
Hieraus folgt die Behauptung sofort.
2
Satz 10.5 Die Funktion f sei auf I = [a, b] integrierbar, c ∈ R. Dann ist auch
die Funktion cf auf I = [a, b] integrierbar, und es gilt
Z b
Z b
f (x)dx.
(cf )(x)dx = c
a
a
Beweis. Klar.
2
Satz 10.6 Die Funktion f sei auf I = [a, b] integrierbar. Es gelte
m ≤ f (x) ≤ M, x ∈ [a, b] .
Dann gilt
m(b − a) ≤
Z
b
f (x)dx ≤ M (b − a).
a
Beweis. Für jede Zerlegung P des Intervalls I = [a, b] gilt
m(b − a) ≤ U (f, P ) ≤ O(f, P ) ≤ M (b − a).
2
Bemerkung 10.1 (1) Ist a > b, so definiert man
Z b
Z a
f (x)dx := −
f (x)dx.
a
b
Rb
(2) Ist f ≥ 0, so versteht man das Integral a f (x)dx als den Flächeninhalt, der
vom Graphen der Funktion und der x-Achse eingeschlossen wird. Ist f ≤ 0, so
wird dieser Flächeninhalt negativ gezählt.
10 Das Riemannsche Integral
55
+
+
a
_
Abbildung 13: Das Integral als Flächeninhalt
b