Ganzrationale Funktionen

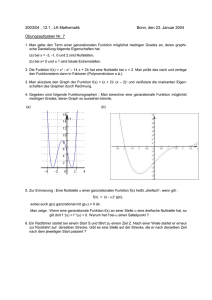
Ganzrationale Funktionen
Eine Dokumentation von
Sandro Antoniol
Klasse 3f
Mai 2003
Ganzrationale Funktionen
Inhaltsverzeichnis:
1.
2.
Einleitung .............................................................................................................................3
Grundlagen ..........................................................................................................................4
2.1.
Symmetrieeigenschaften von Kurven.........................................................................4
2.1.1.
gerade Exponenten.............................................................................................4
2.1.2.
ungerade Exponenten.........................................................................................5
2.1.3.
gemischte Exponenten .......................................................................................5
2.1.4.
Übersicht .............................................................................................................6
3. Nullstellen ............................................................................................................................7
3.1.
Berechnung.................................................................................................................7
3.1.1.
Funktionen ersten Grades ..................................................................................7
3.1.2.
Funktionen zweiten Grades ................................................................................7
3.1.3.
Funktionen dritten Grades ..................................................................................8
4. Quellen...............................................................................................................................11
Sandro Antoniol
Seite 2 / 11
Mai 2003
Ganzrationale Funktionen
1. Einleitung
Definition einer ganzrationalen Funktion:
Eine Funktion heisst ganzrational, wenn man ihren Funktionsterm auf
diese Form bringen kann:
f(x) = a n xn + an-1 xn -1 + … + a 1x1 + a0
Die Zahlen a0 , a1 bis an heissen die Koeffizienten der Potenzen x0 , x1 bis xn . Der Koeffizient
a0 heisst auch das Absolutglied, weil er im Grunde ohne x absolut unveränderlich ist,
während a1x usw. die Variable x dabei haben.
Den Term (mathematischen Ausdruck) auf der rechten Seite der Gleichung bezeichnet man
als Polynom, deshalb ist in vielen Büchern auch von der Polynomfunktion die Rede. Der
höchste vorkommende Exponent n (mit a n ? 0) bestimmt den Grad der Funktion. (auch
genannt den Polynomgrad). Wenn alle Exponenten ungrad sind, so spricht man auch von
einer ungeraden Funktion.
Beispiele:
höchster Exponent
4
2
f1(x) = x – 2x – 4x + 5
Ist eine ganzrationale Funktion 4. Grades, da der
höchste Exponent 4 beträgt. Die Funktion hat folgende
Koeffizienten: a4 = 1, a3 = 0, a2 = 2, a 1 = 4, a0 = 1
f2(x) = 3x5 + 2x3 + ? x
Ist eine ganzrationale Funktion 5. Grades, da der
höchste Exponent 5 beträgt. Da zudem alle Exponenten
ungerade sind, handelt es sich hierbei auch um eine
ungerade Funktion. Die Koeffizienten lauten hier wie
folgt:: a5 = 3, a4, a2, a0 = 0, a3 = 2, a1 = ?
f3(x) = (x2 – 2) 2
Wenn man das Polynom in die Normalform bringt, ist
erkenn bar, dass es sich bei dieser Funktion um eine
gerade, ganzrationale Funktion 4. Grades handelt.
f3(x) = x4 – 2x2 + 1
Der Definitionsbereich einer Funktion besteht aus allen reellen Zahlen, denen man einen
Funktionswert zuordnen kann. Einschränkungen ergeben immer nur diese drei
Rechenoperationen:
Dividieren: ist durch 0 nicht möglich
Ziehen einer Wurzel: ist aus negativen Zahlen nicht möglich
Logarithmieren: ist nur bei positiven Zahlen möglich.
Da bei ganzrationalen Funktion x weder im Nenner, noch unter einer Wurzel oder in einem
Logarithmus vorkommt, haben alle ganzrationalen Funktionen den maximalen
Definitionsbereich D = R, d.h. zu jeder reellen Zahl ist ein Funktionswert berechenbar.
Die Zuordnung x ? f(x).kann man auch geometrisch als Punkt (x | f(x) ) . darstellen.
Die Menge aller solchen Punkte nennt man den Graph oder das Schaubild der Funktion,
oder auch eine Kurve.
Sandro Antoniol
Seite 3 / 11
Mai 2003
Ganzrationale Funktionen
Es gibt nun einige Merkmale, die rasch erkennen lassen, ob bestimmte Eigenschaften
vorliegen. Diese werden im folgenden Kapitel besprochen.
2. Grundlagen
2.1.
Symmetrieeigenschaften von Kurven
2.1.1.gerade Exponenten
Wenn eine Funktion nur gerade Exponenten hat, so ist der Graph symmetrisch zur y-Achse.
Diese Eigenschaft resultiert aus der Tatsache, dass wenn man eine negative Zahl mit einem
geraden Exponenten exponiert, so erhält man den gleichen Wert, wie wenn man die positive
Zahl exponiert hätte. (Minus · Minus = Plus). Dies bedeutet, dass man für die Funktion:
f(x) = ¼ · x4 - 2x2 + 7/4
den gleichen Wert erhält, egal ob man 2, oder –2 für x einsetzt. Somit gilt:
f(x) = f(-x)
Bei geraden Funktion ist der Graph symmetrisch zur y -Achse da f(x) = f(-x)
Sandro Antoniol
Seite 4 / 11
Mai 2003
Ganzrationale Funktionen
2.1.2.ungerade Exponenten
Wenn eine Funktion nur ungerade Exponenten beinhaltet, so ist der Graph
punktsymmetrisch zum Ursprung. Dies bedeutet, dass wenn ich z.B. für x zuerst 3 einsetze,
und anschliessend –3, so erhalte ich als zweites Resultat den invertierten Wert des ersten
Resultates (positiv wird negativ, oder umgekehrt). Am verständlichsten ist diese Eigenschaft,
wenn man das untenstehenden Graphen betrachtet, der aus folgender Funktion resultiert:
f(x) = -1/9 · x3 + x
Graph zur Funktion f(x) = -1/9 · x3 + x
Es lässt sich gut erkennen, dass beim Punkt x = -2 ein y-Wert von etwas weniger als –1 hat,
und bei x = 2 ein y-Wert von etwas weniger als +1 hat.
2.1.3.gemischte Exponenten
Beinhaltet eine Funktion gerade sowie auch ungerade Exponenten, so ist keine Symmetrie
erkennbar.
f(x) = -1/9 · x3 + 2x – 3
Sandro Antoniol
Seite 5 / 11
Mai 2003
Ganzrationale Funktionen
2.1.4.Übersicht
Geht man von der Funktion f(x) = a · xn …aus, so lassen sich die möglichen Verläufe des aus
der Funktion resultierenden Graphen in insgesamt 5 Kategorien unterteilen, je nachdem ob
die Funktionsgleichung aus geraden oder ungeraden Exponenten besteht und ob man für a
einen negativen oder positiven Wert wählt.
1. a > 0 und n = nur gerade
Beispiel Funktion: f(x) = ¼ · x4 + …
Wenn x ? +/- 8 so gilt für f(x) ? 8
2. a < 0 und n = nur gerade
Beispiel Funktion: f(x) = -¼ · x4 + …
Wenn x ? +/- 8 so gilt für f(x) ? -8
3. a > 0 und n = nur ungerade
Beispiel Funktion: f(x) = 1/6 · x3+ …
Wenn x ? 8 so gilt für f(x) ? 8
und wenn x ? - 8 so gilt für f(x) ? - 8
4. a < 0 und n = nur ungerade
Beispiel Funktion: f(x) = -1/6 · x3+ …
Wenn x ? 8 so gilt für f(x) ? - 8
und wenn x ? - 8 so gilt für f(x) ? + 8
5. Gemischt
Wenn die Koeffizienten mal grösser, mal kleiner null sind, und die Exponenten mal
gerade, mal ungerade sind, so lässt sich nur sehr wage eine Vorhersage treffen, wie
der Graph verlaufen wird.
Sandro Antoniol
Seite 6 / 11
Mai 2003
Ganzrationale Funktionen
3. Nullstellen
Eine Nullstelle ist eine Zahl mit dem Funktionswert 0. Dort schneidet oder berührt der Graph
die x-Achse.
Eine ganzrationale Funktion n-ten Grades kann höchstens n reelle Nullstellen haben.
Wie sich anhand der Grafiken im Kapitel 2.1.4 gut entnehmen lässt, besitzen ganzrationale
Funktionen mit nur ungeraden Exponenten mindestens eine Nullstelle. Bei anderen
Funktionen, die diese Eigenschaft nicht erfüllen, lässt sich nicht ausschliessen, dass eine
Funktion gar keine Nullstelle besitzt.
3.1.
Berechnung
Je grösser der grösste Exponent einer Funktionsgleichung ist, desto mehr Nullstellen sind
möglich, und desto schwieriger wird es auch alle Nullstellen zu berechnen. Um nicht den
Rahmen dieser Dokumentation zu sprengen, beschränke ich mich hier auf die Berechnung
der Nullstellen einer Funktion bis maximal dritten Grades. Wer mehr wissen möchte über die
Berechnung von Nullstellen bei Funktionen höheren Grades, findet Informationen in den, im
Quellen-Verzeichnis (Kapitel 4) angegebenen Internetseiten.
3.1.1.Funktionen ersten Grades
Bei einer Funktion ersten Grades handelt es sich ganz schlicht um eine Gerade, welche
bekanntlich nur eine Nullstelle besitzen kann. Um die Nullstelle zu berechnen setzt man für
f(x) = 0 ein, und löst die Funktionsgleichung nach x auf.
Beispiel:
f(x) = -3x + 4
0 = -3x + 4 | +3x
3x = 4 | :4
x=¾
N = (¾,0)
3.1.2.Funktionen zweiten Grades
Bei Funktionen zweiten Grades kann es maximal zwei Nullstellen geben. Zur Berechnung
dieser zwei möglichen Nullstellen setzt man ebenfalls f(x) = 0, und bedient sich dann der
bekannten Lösungsformel für quadratische Gleichungen:
x1,2 =
Sandro Antoniol
- b ± b 2 − 4ac
2a
Seite 7 / 11
Mai 2003
Ganzrationale Funktionen
Beispiel:
f(x) = -2x2 + 3x + 2
0 = -2x2 + 3x + 2
Allgemein Form: f(x) = ax2 + bx +c
a = -2 ; b = 3 ; c = +2
- 3 ± 3 2 − 4( −2 )( 2)
x1,2 =
2(-2)
x1 = -0.5 ; x2 = 2
3.1.3.Funktionen dritten Grades
Die Nullstellen einer Funktion dritten Grades lassen sich durch Polynomdivision berechnen.
Dies Bedingt allerdings, dass mindestens ein Wert für x, an dem f(x) = 0 ist, gegeben ist.
Denn dadurch lässt sich die Funktion auch in der Form:
f(x) = (x – x1) * f1(x) darstellen.
x1 = der Wert damit die Funktion 0 ergibt.
Der Faktor (x – x1) heisst Linearfaktor,
f1(x) ist das sog. 1. reduzierte Polynom vom Gerade (n-1)
Durch die Abspaltung eines Linearfaktors erhalten wir das reduzierte Polynom f1(x) vom
Gerade (n-1). Das heisst, wenn f(x) eine Funktion dritten Grades ist, so ist f1(x) eine Funktion
zweiten Grades. Wenn f1(x) berechnet ist, kann man mittels Lösungsformel für quadratische
Gleichungen die restlichen zwei Nullstellen berechnen. (Siehe Kapitel 3.1.2)
Berechnungs-Beispiel:
f(x) = x3 – 2x2 - 5x + 6 mit einer Nullstelle x1 = 1
f(x) = (x – x1) * f1(x)
| : (x – x1)
f1(x) = f(x) / f1(x)
1. Zuerst dividieren wir das höchste Glied von f(x) durch das höchste Glied von (x – 1), d.h.
wir rechnen x3/x = x2 und schreiben das Ergebnis hinter das Gleichheitszeichen.
geteilt durch
gleich
(x3 – 2x2 - 5x + 6) : (x – 1) = x2
2. Nun multiplizieren wir das Ergebnis (2x2) mit (x – 1) und schreiben das Ergebnis unter das
Polynom f(x). Dabei schreiben wir die Glieder gleichen Grades untereinander:
(x3 – 2x2 - 5x + 6) : (x – 1) = x2
x3 – x2
gleich
Sandro Antoniol
mal
Seite 8 / 11
Mai 2003
Ganzrationale Funktionen
3. Dieses Ergebnis (x3 – x2) ziehen wir gliedweise vom Polynom f(x) ab, und schreiben es
unter den Strich:
(x3 – 2x2 - 5x + 6) : (x – 1) = x2
- (x3 – x2
)
2
- x - 5x + 6
Das negative Vorzeichen vor der Klammer wird normalerweise nicht geschrieben.
4. Schritt 1-3 wiederholen sich nun immer wieder: Nun dividieren wir das höchste Glied
dieses Restes durch das höchste Glied von (x – 1) , d.h. wir rechnen -x2/x und schreiben
das Ergebnis (-x) hinter das Gleichheitszeichen:
(x3 – 2x2 - 5x + 6) : (x – 1) = x2 - x
x3 – x 2
- x2 - 5x + 6
5. Nun multiplizieren wir wieder das Ergebnis (-x) mit (x – 1) und schreiben das Resultat
unter den Rest:
(x3 – 2x2 - 5x + 6) : (x – 1) = x2 - x
x3 – x 2
- x2 - 5x + 6
- x2 + x
6. Wir subtrahieren wieder die untereinander stehenden Glieder:
(x3 – 2x2 - 5x + 6) : (x – 1) = x2 - x
x3 – x 2
- x2 - 5x + 6
- x2 + x
- 6x + 6
7. Von nun an werden die Schritte 4 bis 6 solange wiederholt, bis der Rest 0 auftritt, oder der
Rest ein Polynom ist, dessen Grad kleiner als der Grad von (x – 1) * ist:
(x3 – 2x2 - 5x + 6) : (x – 1) = x2 – x - 6
x3 – x 2
- x2 - 5x + 6
- x2 + x
- 6x + 6
- 6x + 6
0
*
Zum Beispiel bei der Division x/x
Sandro Antoniol
3
Seite 9 / 11
Mai 2003
Ganzrationale Funktionen
8. Wir haben für f1(x) das Resultat „x2 – x – 6“ erhalten. Um nun die zwei weiteren Nullstellen
zu berechnen kann man die Lösungsformel für quadratische Funktionen verwenden.
Allerdings erkennt ein geschultes Auge sofort, dass es sich beim erhaltenen Resultat um ein
Produkt einer Binomischen Formel handelt. Deshalb lässt sich das Resultat auch so
darstellen:
f1(x) = (x-3)(x+2)
Weil die Multiplikation von f1(x) mit (x – 1) die ursprüngliche Funktion f(x) ergibt, können wir
nun die Funktionsgleichung für f(x) auch in Form eines Produktes darstellen:
f(x) = (x - 1)(x – 3)(x + 2)
Damit f(x) = 0 ist, muss x so gewählt werden, dass mindestens ein Faktor 0 ist. Dies
bedeutet, dass in mindestens einer Klammer die Summe gleich 0 sein muss. Da wir drei
verschiedene Klammern haben, gibt es für x drei verschiedene Werte, damit das Produkt 0
ergibt:
x1 = 1
x2 = 3
x3 = -2
Daraus ergeben sich nun folgende drei Nullstellen:
N1 = (1/0)
N2 = (3/0)
N3 = (-2/0)
Graph der Funktion f(x) = x 3 – 2x2 - 5x + 6
Wie schon erwähnt, kann man die Nullstellen nach der Polynomdivision auch mit der
Lösungsformel für quadratische Gleichungen berechnen. Wenn aber als Resultat schon ein
Produkt einer Binomischen Formel heraus kommt, so ist man mit der Produktdarstellung
schneller.
Sandro Antoniol
Seite 10 / 11
Mai 2003
Ganzrationale Funktionen
4. Quellen
Internet:
http://home.arcor.de/loknar/mathe/ganzrationale_funktionen.doc
http://www.mathe-aufgaben.de/mathehilfen/matheabitur/Funktionen/gara/18011%20Funktionen%202%20SOD.pdf
http://www.steinwaldgym.de/ganzrat.htm
Andere:
Arbeitsblatt „Ganzrationale Polynomfunktionen“ aus dem Freifachkurs Mathematik von Herrn
G. Kopacsy
Sandro Antoniol
Seite 11 / 11
Mai 2003