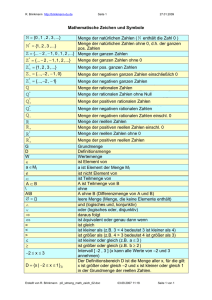
Handout Britta Zach - Mathematik und ihre Didaktik

g-adische Darstellung rationaler Zahlen
Vortrag im Modul „Berufsbezogenes Fachseminar“
Britta Zach | WS 2014/15 | 03.11.2014
Dozent: Prof. Dr. Jürg Kramer
Inhaltsverzeichnis
1 Vorüberlegungen und Wiederholung
2
1.1
Zahlen vs. Zahlendarstellungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2
1.2
Dezimaldarstellung natürlicher Zahlen . . . . . . . . . . . . . . . . . . . . . . . .
2
1.3
Dezimaldarstellung ganzer Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
2 g-adische Darstellung ganzer Zahlen
4
2.1
g-adische Darstellung natürlicher Zahlen . . . . . . . . . . . . . . . . . . . . . . .
4
2.2
g-adische Darstellung ganzer Zahlen . . . . . . . . . . . . . . . . . . . . . . . . .
7
3 Die Menge der rationalen Zahlen
7
3.1
Definitionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
3.2
Rechenoperationen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
3.3
Anordnung der rationalen Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
3.4
Betrag . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
4 g-adische Darstellung rationaler Zahlen
9
4.1
Beweis für nicht-periodische g-adische Brüche . . . . . . . . . . . . . . . . . . . .
10
4.2
Periodische g-adische Brüche . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
5 Quellen
12
1 Vorüberlegungen und Wiederholung
1.1 Zahlen vs. Zahlendarstellungen
Um unterschiedliche Repräsentationsformen von Zahlen zu untersuchen, ist es erforderlich, sich
den Unterschied zwischen Zahlen (als abstrakten mathematischen Objekten) und Zahlendarstellungen (Namen, Bezeichnungen) bewusst zu machen. Hier scheinen zeichentheoretische Konzepte
hilfreich zu sein. Sowohl, um über Dinge nachzudenken, als auch, um sich über Dinge zu verständigen, brauchen wir Bezeichnungen. Dabei fallen die Dinge jedoch nicht mit diesen Bezeichnungen
zusammen: Jede natürliche Zahl beispielsweise ist durch Axiome definiert, nicht durch den Namen, den wir ihr geben (z.B. „10“). Dieses Phänomen hat noch eine weitere Dimension: Man
kann die These vertreten, dass auch die lautliche oder schriftliche Repräsentation dieses Namens
nicht mit dem Namen selbst zusammen fällt. Das Verhältnis dieser drei Aspekte eines Zeichens
ist Gegenstand diverser sprachwissenschaftlicher Theorien:
(Quelle: http://www.hispanoteca.eu/Lexikon%2520der%2520Linguistik/sa/Semiotisches%2520
Dreieck-Eco-Zeichen-30.gif, 02.11.2014)
1.2 Dezimaldarstellung natürlicher Zahlen
Unser Ziel ist es, die g-adische Darstellung rationaler Zahlen mithilfe einer natürlichen Zahl g zu
beschreiben. Hierzu betrachten wir zunächst die Dezimaldarstellung rationaler Zahlen, die bereits in der vorigen Woche thematisiert wurde, als vertrauten Sonderfall. Diese Vorüberlegungen
werden wir auf die natürlichen und die ganzen Zahlen beschränken.
Die Existenz einer Dezimaldarstellung für jede natürliche Zahl ist in folgendem Satz verankert,
den wir am 27.10.2014 kennen gelernt haben.
Satz 1.1. Sei n 2 N, n 6= 0. Dann existiert ein k 2 N, sodass sich n eindeutig darstellen lässt
in der Form
n = bk · 10k + bk
1
· 10k
1
mit b0 , . . . , bk 2 {0, . . . , 9}, bk 6= 0.
2
+ . . . + b1 · 101 + b0 · 100
Um eine im Folgenden besser handhabbare Variante dieses Satzes zu etablieren, formen wir diese
Darstellung von n wie folgt um:
n = bk · 10k + bk
1
· 10k
1
+ . . . + b1 · 101 + b0 · 100
= b0 · 100 + b1 · 101 + . . . + bk · 10k
k
X
=
bi 10i .
i=0
Entsprechend kann nun auch Satz 1.1 umgeformt werden.
Satz 1.2 (synonym zu Satz 1.1). Jede natürliche Zahl n besitzt eine eindeutige Darstellung der
Form
n=
k
X
bi 10i
i=0
mit b0 , . . . , bk 2 {0, . . . , 9}, bk 6= 0.
1.3 Dezimaldarstellung ganzer Zahlen
Vertraut ist ebenfalls, dass sich eine ganze Zahl einfach darstellen lässt, indem ein Vorzeichen
vor die Darstellung der betragsgleichen natürlichen Zahl gesetzt wird. Dass dies funktioniert, ist
in einem weiteren Satz verankert.
Satz 1.3. Jedes Ziffernsystem zur Darstellung von N induziert ein Ziffernsystem zur Darstellung
von Z.
Beweis. Kornhuber/Schütte/Fest (2006), S. 8.
Entsprechend kann Satz 1.2 für die Menge der ganzen Zahlen erweitert werden.
Satz 1.4. Jede ganze Zahl z besitzt eine eindeutige Darstellung der Form
z=±
k
X
bi 10i
i=0
mit b0 , . . . , bk 2 {0, . . . , 9}, bk 6= 0.
Beweis. Folgt aus Satz 1.2 und Satz 1.3.
Beispiel 1.1.
765410 = 4 · 100 + 5 · 101 + 6 · 102 + 7 · 103
= b0 · 100 + b1 · 101 + b2 · 102 + b3 · 103
=
k
X
bi 10i
i=0
mit k = 3, b0 = 4, b1 = 5, b2 = 6, b3 = 7. Die Bedingungen b0 , . . . , bk 2 {0, . . . , 9} und
bk 6= 0 sind erfüllt.
3
2 g-adische Darstellung ganzer Zahlen
Vom Spezialfall der Dezimaldarstellung kommen wir nun zur g-adischen Darstellung natürlicher
und ganzer Zahlen. Statt wie vorher die Darstellung mithilfe von Zehnerpotenzen betrachten wir
nun Darstellungen mithilfe anderer natürlicher Zahlen g.
2.1 g-adische Darstellung natürlicher Zahlen
Satz 2.1. Sei g 2 N, g
2, Sg = {0, . . . , g
eindeutige Darstellung der Form
n=
1} ⇢ N. Dann besitzt jede natürliche Zahl n eine
k
X
bi g i
i=0
mit b0 , . . . , bk 2 Sg und bk 6= 0.
Beweis. Zu zeigen sind die Existenz einer solchen Darstellung für jede natürliche Zahl n sowie
deren Eindeutigkeit.
a) Existenz
a.1) Nach dem Satz zur Division mit Rest existieren für das gewählte n 2 N eindeutig bestimmte
a0 , b0 2 N mit 0  b0 < g, sodass gilt
n = a 0 · g + b0 .
a.2) Betrachte a0 . Wieder existieren eindeutig bestimmte a1 , b1 2 N mit 0  b1 < g, sodass gilt
a 0 = a 1 · g + b1 .
Dieses Vorgehen kann durch sukzessive Division mit Rest beliebig fortgesetzt werden:
0  b0 < g, a0 , b0 2 N eindeutig bestimmt;
n = a 0 · g + b0 ,
0  b1 < g, a1 , b1 2 N eindeutig bestimmt;
a 0 = a 1 · g + b1 ,
0  b2 < g, a2 , b2 2 N eindeutig bestimmt;
a 1 = a 2 · g + b2 ,
...
Allgemein lässt sich dies wie folgt schreiben: Für alle i 2 N existieren eindeutig bestimmte
ai+1 , bi+1 2 N mit 0  bi+1 < g, sodass gilt
ai = ai+1 · g + bi+1 .
a.3) Dabei kann man vermuten, dass für alle i 2 N gilt
ai+1  ai .
Angenommen es existiert ein i 2 N mit ai+1 > ai . Dann folgt ai+1 > ai+1 · g + bi+1 ; dies ist aber
ein Widerspruch zu ai+1
0, bi+1
0 und g
2.
4
a.4) Weiter gilt: Angenommen es existiert ein i 2 N mit ai = ai+1 . Dann folgt
ai+1 · g + bi+1 = ai+1 ,
) ai+1 · (g
)
da g
2, ai+1
0 und bi+1
1) + bi+1 = 0,
ai+1 = bi+1 = 0,
0. Insgesamt gilt nun für alle i 2 N
ai > ai+1 _ ai = ai+1 = bi+1 = 0.
Der Algorithmus stoppt also erst für ai = 0.
a.5) Definiere
k := min {i 2 N ai = ai+1 = bi+1 = 0}.
Dann gilt ak
1
6= ak = 0 ) bk 6= 0, sodass bk der letzte nicht-verschwindende Rest der sukzessi-
ven Division mit Rest ist. Führe eine sukzessive Division mit Rest wie folgt durch:
n
=
a 0 · g + b0 ,
a0
=
a 1 · g + b1 ,
a1
=
a 2 · g + b2 ,
...
1
=
0 · g + bk ,
ak
=
0 · g + 0 = 0.
ak
a.6) Zeige nun, dass gilt
n=
k
X
bi g i
i=0
mit b0 , . . . , bk 2 Sg und bk 6= 0. Es gilt:
ak
1
= bk ,
) ak
2
= bk · g + bk
) ak
3
= (bk · g + bk
1,
1 )g
= b k · g 2 + bk
+ bk
2
· gk
3
1
· g + bk
...
)
)
a0 = (bk · g k
= bk · g k
2
1
n = (bk · g k
k
+ bk
+ bk
1
=
k
X
1
· gk
1
+ bk
= bk · g + bk
1
1
·g
· gk
k 1
bi g i .
i=0
5
2
+ . . . + b3 · g + b2 )g + b1
+ . . . + b2 · g + b 1 ,
2
+ . . . + b2 · g + b1 )g + b0
+ . . . + b 1 · g + b0 ,
2,
b) Eindeutigkeit
b.1) Angenommen es existieren für k, l 2 N, b0 , . . . , bk und c0 , . . . , cl 2 N mit
n=
k
X
l
X
i
bi g =
i=0
ci g i .
(1)
i=0
Wenn es sich hierbei um unterschiedliche Darstellungen von n handeln soll, muss entweder k 6= l
gelten oder aber es existiert mindestens ein i 2 {1, . . . , k} [ {1, . . . , l} mit bi 6= ci .
b.2) Zeige zunächst, dass aus Gleichung (1) aber folgt k = l. Angenommen, es gilt k 6= l. Dann
gilt entweder k > l oder l > k. Nehme o.B.d.A an, dass k > l. Dann folgt k
k
X
bi g i
1 · g l+1 + 0 · g k
i=0
1
l + 1, sodass gilt
+ . . . + 0 · g 0 = g l+1 .
Gleichzeitig gilt für die zweite Darstellung von n
l
X
i=0
ci g i  (g
= (g
= (g
=g
l+1
<g
l+1
1) · g l + (g
1) ·
1) ·
l
X
1) · g l
1
1) · g 0
+ . . . + (g
gi
i=0
g l+1
g
1
1
1

k
X
bi g i
zu (1).
i=0
b.3) Zeige, dass aus (1) weiter folgt bk = ck . Angenommen, es gilt bk 6= ck . Dann gilt entweder
bk > ck oder ck > bk . Nehme o.B.d.A. an, dass bk > ck . Dann folgt bk
k
X
bi g i
i=0
(ck + 1) · g k + 0 · g k
1
ck + 1, sodass gilt
+ . . . + 0 · g 0 = (ck + 1) · g k .
Gleichzeitig gilt für die zweite Darstellung von n
k
X
i=0
ci g i  ck · g k + (g
1) · g k
= ck · g + (g
1) ·
k 1
X
= ck · g k + (g
1) ·
g
= (ck + 1) · g k
1
k
< (ck + 1) · g k 
i=0
+ . . . + (g
gi
i=0
gk
k
X
6
1
bi g i
1
1
zu (1).
1) · g 0
b.4) Aus k = l und bk = ck folgt wiederum
k
X
i
bi g =
i=0
l
X
i=0
i
k
c i g , bk · g +
k 1
X
i=0
i
k
bi g = c k · g +
k 1
X
i=0
i
ci g ,
k 1
X
i
bi g =
i=0
Entsprechend kann nun analog zu vorigem Vorgehen gezeigt werden, dass bk
k 1
X
ci g i .
i=0
1
= ck
1
gilt. Durch
sukzessive Anwendungen der Schritte aus b.2 kann wiederum gezeigt werden, dass gilt
bi = ci 8 i 2 {0, . . . , k}.
Insgesamt kann damit die Eindeutigkeit der g-adischen Darstellung von n gezeigt werden.
Beispiel 2.1 (Dualdarstellung natürlicher Zahlen). Es gilt g = 2, Sg = {0, 1} ⇢ N.
10102 = 0 · 20 + 1 · 21 + 0 · 22 + 1 · 23 = 2 + 8 = 1010 .
Beispiel 2.2 (Umwandeln von Dezimal- in Dualdarstellung). Wir suchen nach der Dualdarstellung von 3310 .
33 : 2 = 16,
Rest = 1;
16 : 2 = 8,
Rest = 0;
8 : 2 = 4,
Rest = 0;
33 = 2 · 16 + 1 · 20
= 2(2 · 8 + 0) + 1 · 20 = 22 · 8 + 0 · 21 + 1 · 20
= 22 (2 · 4 + 0) + 0 · 21 + 1 · 20
= 23 · 4 + 0 · 22 + 0 · 21 + 1 · 20
4 : 2 = 2,
Rest = 0;
= 23 (2 · 2 + 0) + 0 · 22 + 0 · 21 + 1 · 20
= 24 · 2 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20
2 : 2 = 1,
Rest = 0;
= 24 · (2 + 0) + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20
= 25 · 1 + 0 · 24 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20
1 : 2 = 0,
Rest = 1;
0 : 2 = 0,
Rest = 0;
= 1 · 25 + 0 · 24 + 0 · 23 + 0 · 22 + 0 · 21 + 1 · 20 .
) 3310 = 1000012 .
2.2 g-adische Darstellung ganzer Zahlen
Satz 2.2. Sei g 2 N, g
1} ⇢ N. Dann besitzt jede ganze Zahl z eine
2, Sg = {0, . . . , g
eindeutige Darstellung der Form
z=±
mit b0 , . . . , bk 2 Sg und bk 6= 0.
k
X
bi g i
i=0
Beweis. Folgt aus Satz 2.1 und Satz 1.3.
3 Die Menge der rationalen Zahlen
Die folgende Beschreibung der rationalen Zahlen orientiert sich an der Darstellung von Kramer
(2008), S.130 f.
7
3.1 Definitionen
Die Menge der rationalen Zahlen lässt sich mithilfe von Äquivalenzklassen definieren. Dazu wird
zunächst die Äquivalenzrelation „⇠“ auf dem kartesischen Produkt Z ⇥ (Z\{0}) definiert.
Definition 3.1. Für (u, v), (x, y) 2 Z⇥(Z\{0}) sei die Äquivalenzrelation „⇠“ wie folgt definiert:
(u, x 2 Z; v, y 2 Z\{0}).
(u, v) ⇠ (x, y) :, u · y = x · v
Die Menge Q der rationalen Zahlen wird nun als Menge von Äquivalenzklassen
u
v
= [u, v] zu den
Paaren (u, v) 2 Z ⇥ (Z\{0}) definiert.
Definition 3.2.
Q :=
nu
v
o
(u, v) 2 Z ⇥ (Z\{0}) .
Die Menge Z der ganzen Zahlen lässt sich als Teilmenge von Q betrachten. Dazu nutzt man die
Tatsache, dass durch die Zuordnung u ! [u, 1] =
eine Injektion zwischen
Z und
n
o Q induziert
u
wird. Man identifiziert die Menge der ganzen Zahlen Z mit der Menge 1 u 2 Z .
u
1
Definition 3.3. u = u1 .
Lemma 3.1. Aus der Definition folgt, dass für alle
u
(z · u)
=
v
(z · v)
8
u
v
2 Q gilt
z 2 Z\{0}.
3.2 Rechenoperationen
Definition 3.4. Auf Q werden die Verknüpfungen „+“, „ “ „· “ und „ : “ für alle
folgt definiert:
i) Addition:
ii) Subtraktion:
iii) Multiplikation:
u x
v, y
2 Q wie
u x
uy + xv
+ :=
.
v
y
vy
u
v
x
uy xv
:=
.
y
vy
u x
u·x
· :=
.
v y
v·y
iv) Division:
u x
u·y
: :=
v y
v·x
✓
◆
x
6= 0 .
y
Aus dieser Definition folgt, dass die Definition der Rechenoperationen in den rationalen Zahlen
verträglich mit den Definitionen der Rechenoperationen in den ganzen Zahlen ist. Weiter folgt,
dass die Menge Q der rationalen Zahlen mit den Verknüpfungen „+“ und „·“ einen Körper (Q, +, ·)
bildet.
Satz 3.1.
i)
0
1
ist das neutrale Element bezüglich der Verknüpfung „+“.
8
ii)
1
1
ist das neutrale Element bezüglich der Verknüpfung „·“.
iii) Für
u
v
2 Q ist das bezüglich „+“ inverse Element
u
v
iv) Für
u
v
2 Q\{0} ist das bezüglich „·“ inverse Element ( uv )
u
v
gegeben durch
1
u
v
=
gegeben durch
v
u
.
.
Insbesondere sind Kommutativität, Assoziativität und Distributivität von „+“ und „·“ auch in
den rationalen Zahlen gegeben.
3.3 Anordnung der rationalen Zahlen
Die Definition der Relationen „<“ bzw. „“ wird von der Menge Z der ganzen Zahlen auf die
Menge Q der rationalen Zahlen erweitert.
Definition 3.5. Für zwei rationale Zahle
u
x
< ,
v
y
(
u · y < x · v,
u
x
 ,
v
y
(
bzw.
u x
v, y
2 Q gilt
falls
v > 0,
y>0
oder
v < 0,
y < 0,
u · y > x · v,
falls
v > 0,
y<0
oder
v < 0,
y > 0,
u · y  x · v,
falls
v > 0,
y>0
oder
v < 0,
y < 0,
falls
v > 0,
y<0
oder
v < 0,
y > 0.
u·y
x · v,
Analog lassen sich auch die Relationen „>“ bzw. „ “ auf die Menge Z der ganzen Zahlen erweitern. Auf Grundlage dieser Definition gilt der folgende Satz.
Satz 3.2. Q wird mit der Relation „<“ zur geordneten Menge, d.h. es gilt für alle q1 , q2 , q3 2 Q:
i) Entweder es gilt q1 < q2 oder q2 < q1 oder q1 = q2 .
ii) Die Relationen q1 < q2 , q2 < q1 , q1 = q2 schließen sich gegenseitig aus.
iii) Sei q1 < q2 und q2 < q3 , dann q1 < q3 .
Analog für die Relation „>“.
3.4 Betrag
Definition 3.6. Für eine rationale Zahl
u
v
8
>
>
<
2 Q ist der Betrag | uv | von
u
:=
>
v
>
:
u
u
, falls
v
v
u
v
wie folgt definiert:
0,
u
u
, falls < 0.
v
v
4 g-adische Darstellung rationaler Zahlen
Der Satz zur g-adischen Darstellung kann auch auf die rationalen Zahlen erweitert werden.
Satz 4.1. Sei g 2 N, g
2, Sg = {0, . . . , g
eindeutige Darstellung der Form
q=±
mit k 2 N, b
i
1} ⇢ N. Dann besitzt jede rationale Zahl q eine
1
X
b ig
i
i= k
2 Sg für alle i 2 { k, k + 1, k + 2, . . . }.
9
Vorüberlegung. Um zu zeigen, dass die Darstellung ganzer Zahlen in Anlehnung an Satz 4.1
mit der Darstellung in Anlehnung an Satz 2.1 übereinstimmt, nehmen wir folgende Umformung
vor: Seien b0 , . . . , bk 2 Sg und bk 6= 0. Dann gilt
z=±
mit k 2 N, b
i
k
X
i=0
bi g i = ±
0
X
b ig
i
i= k
2 Sg für alle i 2 { k, k + 1, k + 2, . . . }.
Statt diesen Darstellungswechsel vorzunehmen, hätte auch von vorneherein die Existenz und
Eindeutigkeit der Darstellung nach Satz 4.1 für alle ganzen bzw. natürlichen Zahlen gezeigt
werden können. Zunächst soll dieser Satz anhand eines Beispiels veranschaulicht werden.
Beispiel 4.1 (Darstellung rationaler Zahlen als Dezimalbruch). Sei q =
127
100
27
=
+
100
100 100
27
= 1 · 100 +
100
0
= 1 · 10 + 27 · 10
= 1 · 100 + 2 · 10
=
1
X
b ig
u
v
=
127
100
2 Q. Es gilt
2
1
+ 7 · 10
2
i
i= k
mit k = 0, b0 = b
k
= 1, b
1
= 2, b
2
= 7 und b
i
= 0 für alle i > 2.
4.1 Beweis für nicht-periodische g-adische Brüche
Ein Beweis des Satzes im eigentlichen Sinne wird nur unter der Beschränkung auf einen Spezialfall
geführt, indem an einer bestimmten Stelle des Beweises eine Vorannahme getroffen wird. Im
darauffolgenden Kapitel wird der Fall betrachtet, dass diese Annahme nicht zutrifft. Für diesen
Fall wird allerdings kein Beweis geliefert, sondern nur ein weiterer, diesen Fall näher bringender
Satz bewiesen.
Beweis.
a) Existenz
Sei q =
x
y
2 Q, (x 2 N, y 2 Z\{0}). Unter Berücksichtigung der Betragsbildung können wir
O.b.d.A q > 0 setzen.
a.1) Wir isolieren den ganzzahligen Anteil von q, indem wir q1 , q2 definieren als
q1 := max {n 2 N | n  q},
q2 := q
q1 .
Entsprechend gilt 0  q2 < 1. Weiter wissen wir, dass 0 = q2 genau dann gilt, wenn es sich
bei q um eine ganze Zahl handelt. Um diesen Fall, der bereits durch Satz 2.1 abgedeckt wird,
auszuklammern, nehmen wir an, dass 0 < q2 < 1 gilt. Wir wissen bereits, dass q1 in eindeutiger
10
Weise dargestellt werden kann in der Form
q1 = ±
k
X
0
X
i
bi g = ±
i=0
b ig
i
i= k
mit b0 , . . . , bk 2 Sg .
a.2) Betrachte nun q2 :
Wir definieren a0 := q2 , multipilizieren a0 sukzessive mit g und stellen das Ergebnis jeweils wieder
als Summe eines natürlichen (im allgemeineren Fall ganzzahligen) Anteils b
eines rationalen Anteils a
i
2 Q, 0 < a
i
Multiplikationsschritts bezeichnet:
i
2 N, b
i
> 0, und
< 1, dar, wobei i 2 N jeweils die Nummer des
a0 · g = b
1
+a
1,
a
1
·g =b
2
+a
2,
a
2
·g =b
3
+a
3,
...
Folgende Definition von b
dass b
i
für alle
i
und a i , die mit diesem Algorithmus verträglich ist, sichert dabei,
i 2 { 1, 2, . . . } in Sg liegt:
b
i
:= max
a
i
:= a
n
n2N na
(i 1)
·g
(i
b i.
o
·
g
,
1)
a.3) Annahme: Wir betrachten hier nur den Fall, dass ein n 2 N existiert, für das der Algorithmus zu folgendem Ergebnis führt:
a
(n 1)
·g =b
n
+ 0,
wobei n definiert wird als
n := min
n
i2N
a
i
·g =0+b
Der Algorithmus sieht dann insgesamt wie folgt aus:
a0 · g = b
1
+a
1,
a
1
·g =b
2
+a
2,
a
2
·g =b
3
+a
3,
n
+ 0.
...
a
(n 1)
·g =b
a.4) Zeige, dass gilt
a0 =
n
X
i=1
11
b ig
i
i
o
.
mit b
2 Sg für alle i 2 { k, k + 1, k + 2, . . . }.
i
a
)
)a
n
a
·g =0+b
n
(n 1)
=b
n
= (b
)
...
)
a0 = (b
=b
=
n
·g
1
(n 1)
1
1
n
X
,
+b
+b
·g
1
2
1
·g
+b
1
·g
n
2
)·g
1
+ ... + b
·g
2
=b
n
(n 1)
·g
+ ... + b
·g
(n 1)
n
·g
)·g
1
+b
n
·g
2
,
1
n
b ig i.
i=1
b) Eindeutigkeit. Dieser Beweis kann analog zum Eindeutigkeitsbeweis von Satz 2.1 geführt
werden. Für q1 und q2 existieren also eindeutige Darstellungen der Form
q1 = ±
mit b
i
0
X
b ig i,
i= k
q2 = ±
n
X
b ig
i
i=1
2 Sg für alle i 2 { k, k + 1, k + 2, . . . }. Die Zahl q kann damit in eindeutiger Weise
dargestellt werden als
q=±
mit k 2 N, b
i
1
X
b ig
i
i= k
2 Sg für alle i 2 { k, k + 1, k + 2, . . . }, b
i
= 0 für alle i > n.
4.2 Periodische g-adische Brüche
Wir betrachten den Fall, dass kein n 2 N existiert, für das der Algorithmus zu folgendem Ergebnis
führt:
a
(n 1)
·g =0+b
n.
Unser Algorithmus bricht in diesem Fall nicht ab. Wir werden diesen Fall im nächsten Vortrag
ausführlich diskutieren und sehen, dass die zugehörige Darstellung periodisch ist.
5 Quellen
• Kornhuber, Ralf; Schütte, Christof; Fest, Andreas (2006): Mit Zahlen Rechnen. Computerorientierte Mathematik I. (Skript zur gleichnamigen Vorlesung im WS 2005/2006). Abgeru-
fen unter: http://www3.math.tu-berlin.de/Vorlesungen/SS07/DiskrMaLS/MitZahlenRechnen.pdf
(06.11.2014)
• Kramer, Jürg (2008): Zahlen für Einsteiger. Wiesbaden : Friedrich Vieweg & Sohn Verlag.
Als Online-Version abgerufen unter http://link.springer.com/book/10.1007/978-3-8348-94236/page/1 (abgerufen am 19.03. 2013)
• http://www.hispanoteca.eu/Lexikon%2520der%2520Linguistik/sa/Semiotisches%2520DreieckEco-Zeichen-30.gif (02.11.2014)
12