( ) ( )t

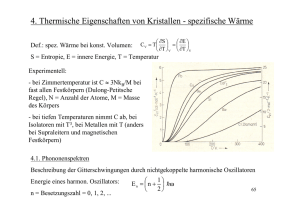
Friedrich-Alexander-Universität Erlangen-Nürnberg
Institut für Werkstoffwissenschaften 6 / AlN
Martensstr. 7, 91058 Erlangen
Vorlesung Grundlagen der WET I
Dr.-Ing. Matthias Bickermann, Prof. Dr. A. Winnacker
C. PHONONEN UND SPEZIFISCHE WÄRME
1. Lineare einatomige Kette
Phononen sind harmonische Gitterschwingungen der an die Gleichgewichtslage
elastisch gebundenen Atome in Kristallen. Die rücktreibende Kraft K ist proportional
zur Auslenkung. Wir betrachten longitudinale Auslenkungen eine eindimensionalen
Kette: K = α ⋅ (a ′ − a ) = α ⋅ u mit der "Federkonstante" α, dem Gleichgewichtsabstand
a und dem Abstand zum Nachbarn a' während der Auslenkung u = a'–a. [Bild 1]
Die
zeitliche
Variation
der
Auslenkung
wird
beschrieben
durch
0
0
u n (t ) = u n ⋅ sin(kna − ω t ) . Hier sind un die Amplitude, k die Wellenzahl, x = na die
örtliche Auslenkung (der n-ten harmonischen Schwingung) und ω die Kreisfrequenz.
2π
2π
(Wellenlänge) und nach der Zeit T =
(Periodendauer) wiederk
ω
holt sich die Amplitude: k (x + λ ) = kx + 2π
und
ω (t + T ) = ω t + 2π . Es gilt:
0
0
0
u n (t ) = u n ⋅ sin(kna − ωt ) = u n ⋅ sin(kna − ωt + 2πn ) = u n ⋅ sin((k + 2aπ )na − ωt ) . Der Kehr1
ω
wert der Periodendauer ist die Frequenz der Schwingung ν =
= . [Bild 2]
2π T
Im Abstand λ =
2. Dispersionsbeziehung
d 2 u n (t )
dt2
(Masse mal Beschleunigung). Die Lösung dieser Differentialgleichung führt auf die
ka
α
π
1 α
sin
sin a bzw. ω = 2π ν = 2
. Damit sind Frequenz
Bedingung: ν =
m
2
π m
λ
und Wellenlänge (bzw. Kreisfrequenz und Wellenzahl) miteinander verknüpft, man
spricht von einer Dispersionsbeziehung ω(k). Weiter folgt: Die Frequenzen der GitterDie Kraft K hängt von der Trägheit (Masse) der Atome ab: K = α ⋅ u n (t ) = m ⋅
schwingungen haben eine Obergrenze! ωmax = 2
α
m
. Und: Zwei elastische Wellen
2π
haben die gleiche Frequenz ω(k), es ist also die Beschreibung der gleia
chen Welle (siehe oben)! Somit reicht es aus, die Dispersionsfunktion im Bereich
⎤ π π⎤
⎥ − a ;+ a ⎥ zu kennen; das ist die "1. Brillouinzone". ωmax wird genau an den Zonen⎦
⎦
π
ka
= 1 ⇔ k = ± . [Bild 3]
grenzen erreicht, denn aus sin
2
a
mit Δk =
3. Akustische Wellen (Kontinuumsnäherung)
ka π a
α ka
α πa
=2
=
<< 1, man darf sin(x) ≈ x nähern: ω ≈ 2
.
2
λ
m 2
m λ
Man erhält eine lineare Beziehung ω = c ⋅ k mit der Ausbreitungsgeschwindigkeit
α a2
c = λ ⋅ν =
. Diese ist aus der Elastizitätstheorie wohlbekannt (Wasser- und
m
E
2π
2π E
Schallwellen), wo gilt: c =
, also ω =
c=
mit dem Elastizitätsmodul E
Für λ >> a gilt
ρ
λ
λ
ρ
und der Dichte ρ. Mit der Näherung oben ergibt sich durch Koeffizientenvergleich:
2 E
α
E
E ⋅m
; α=
und schließlich ωmax =
.
a=
2
a ρ
ρ
m
ρ ⋅a
Die maximalen Frequenzen νmax liegen typischerweise im Bereich 1012…1013 Hz, das
ist infrarote Strahlung. Phononen werden daher mittels IR-Spektroskopie untersucht.
4. Lineare zweiatomige Kette
Die
Dispersionsbeziehung
⎛ 1
1 ⎞
⎟⎟ ± α
ω = α ⎜⎜
+
⎝ M1 M 2 ⎠
2
einer
linearen
zweiatomigen
Kette
lautet:
2
⎛ 1
1 ⎞
4 sin 2 (k ⋅ a )
⎜⎜
⎟⎟ −
. [Bild 4]
+
M1 M 2
⎝ M1 M 2 ⎠
Die quadratische Lösung hat zwei Zweige, den optischen Zweig ω+ und den akustischen Zweig ω–. Ihren Namen haben Sie nach der üblichen Anregungsart: Optische
Schwingungen werden durch elektromagnetische Felder (Licht), akustische durch
mechanische Krafteinwirkung hervorgerufen. [Bild 5]
⎛ 1
1
+
Für k → 0 kommt man auf ω + (0 ) = 2α ⎜⎜
⎝ M1 M 2
louinzone ist ω + ( 2πa ) =
⎞
⎟⎟; ω − (0 ) = 0 . Am Rand der Bril⎠
2α
2α
; ω− ( 2πa ) =
. In jedem Fall wird ω+ >ω–, d.h. die DisM1
M2
persionszweige schneiden sich nicht. Es entsteht eine sog. "phononische Bandlücke". Mit Frequenzen zwischen ω − ( 2πa ) und ω + ( 2πa ) können keine Gitterschwingungen
angeregt werden, Licht in diesem Wellenlängenbereich wird nicht absorbiert (Reststrahlenband in der IR-Spektroskopie). [Bild 6]
5. Dreidimensionale Betrachtung
Ein dreidimensionales monoatomares Gitter erzeugt unabhängige Dispersionsbeziehungen für eine longitudinale (in Ausbreitungsrichtung) und zwei transversale (senkrecht zur Ausbreitungsrichtung) Wellen. Ein biatomares Gitter hat entsprechend drei
akustische und drei optische Zweige. In Kristallen hoher Symmetrie können die zwei
transversalen Wellen jeweils entartet sein, d.h. ihre Dispersionskurven sind gleich.
Für k = 0 treffen die drei akustischen Zweige (bei ω = 0) sowie die drei optischen
Zweige (bei ω ≠ 0, siehe oben) zusammen. Ansonsten haben die longitudinalen Wellen in der gesamten Brillouinzone jeweils größere Kreisfrequenzen ω als die transversalen. [Bild 7]
7. Spezifische Wärme nach Dulong-Petit
Bei einer endlichen Temperatur bewegen sich die Atome im Gitter. In einem Kristall
schwingen N Teilchen harmonisch in drei Raumrichtungen, man muss also 3N gekoppelte Oszillatoren betrachten. Nach der statistischen Mechanik hat die mittlere
Energie (UOsz = Ekin + Epot) eines harmonischen Oszillators den Wert UOsz = kT
(Boltzmann-Verteilung). Besteht der Kristall aus einem Mol (= NA) Teilchen, dann ist
seine molare innere Energie bei der Temperatur T: U = 3 N A k T = 3 R T (NA ist die
Avogadrozahl, 6,022 1023 mol–1, R ist die allgemeine Gaskonstante, 8,315 J/(mol K).
⎛ ∂U ⎞
Die spezifische Wärme bei konstantem Volumen ist definiert als CV = ⎜
⎟ . Nach
⎝ ∂T ⎠V
obiger Betrachtung wäre sie temperaturunabhängig: CV = 3 R = 25 J/(mol K). Das ist
das Dulong-Petit'sche Gesetz. Es stellt aber nur bei hohen Temperaturen und großen Atomgewichten die Realität zufriedenstellend dar. Insbesondere beobachtet man
CV → 0 für T → 0, was sich mit obigem Gesetz nicht erklären läst. [Bild 8]
8. Spezifische Wärme nach Einstein
Nach Planck ist die Energie eines Oszillators gequantelt. Die Quantelung der Energien ist En = n h ω. Die Wahrscheinlichkeit, dass ein Oszillator die Energie En hat, ist
−
n hω
P (n ) ~ e kT . Die Besetzung der Energieniveaus ist Boltzmann-verteilt, die Proportionalität wird normiert, indem jeder Oszillator eine Energie haben muss. Die mittlere
hω
≠ kT (Übungsaufgabe).
Energie ist nunmehr U Osz = h ω
e kT − 1
Einstein entwirft 1905 ein Modell, nach dem alle Teilchen auf derselben Frequenz ω
hω
. Für kleine T gilt damit CV → 0, für große T
schwingen, so dass gilt: U = 3N h ω
e kT − 1
nähert sich die Formel dem Dulong-Petit'schen Gesetz an (Näherung für kleine x: ex
→ 1 + x). Das Modell beschreibt den Verlauf von CV(T) besser. Aber die Annahme,
dass alle Teilchen auf derselben Frequenz schwingen, bildet nicht die Realität ab.
9. Spezifische Wärme nach Debye
Nach Debye sind die Schwingungen der Teilchen über ein Frequenzspektrum verteilt. Die Kopplung der Oszillatoren führt wie bei Federpendeln zu Eigenschwingungen. Nach der klassischen Mechanik hat das System 3N Eigenfrequenzen, die entweder gleich- oder gegenphasige erzwungene Schwingungen auslösen. Aus der
Überlegung, dass die zulässigen k-Vektoren ein Punktgitter bilden, und Kugeloberflächen in diesem (dreidimensionalen) Punktgitter Zustände gleicher Energie beinhalten
(Übungsaufgabe), kann die Zustandsdichte D(ω), d.h. die Zahl der Zustände im infini3
ω2
⋅
⋅
V
tesimalen Frequenzintervall [ω; ω+dω], beschrieben werden als D(ω ) =
2π 2
v 03
mit v 0 =
ω
als Schallgeschwindigkeit und V als Kristallvolumen. Da nur 3N Eigenk
schwingungen möglich sind, existiert eine die Maximalfrequenz ωmax, bei der die
Funktion
D(ω)
"abgeschnitten"
wird.
ωmax
∫ D(ω )dω = 3N berechnen zu ωmax = 3
0
Sie
lässt
6π N v
V
2
Für die mittlere innere Energie heißt das: U =
3
0
sowie die Debye-Temperatur θ =
ωmax
∫ D(ω )
3Vh k 3T 3 kT
2π 2v 03 h 3 h
hω max
k
aus
der
Normierung
. [Bild 9]
0
Umformen und Substitution zu U =
sich
hωmax
kT
∫
0
hω
e
hω
kT
dω . Man kommt durch
−1
x3
dx . Hier führt man ωmax
ex −1
ein, ersetzt N durch NA (molare innere
3 θ
θ
3
9Vk 4T 4 N A T x 3
⎛T ⎞ T x
RT
=
9
Energie) und erhält schließlich: U =
dx
⎜
⎟
∫ x dx . Für
3
Vh 3 ∫0 e x − 1
ωmax
⎝ θ ⎠ 0 e −1
hohe Temperaturen nähert sich auch diese Formel dem Dulong-Petit'schen Gesetz,
∞
x3
π4
θ
→ ∞ wird das Integral ∫ x
und man erfür niedrige Temperaturen
dx =
T
15
0 e −1
(
)
3
3
12 4 ⎛ T ⎞
3
⎛T ⎞
⎛ ∂U ⎞
hält U = π 4 RT ⎜ ⎟ ; CV = ⎜
π R ⎜ ⎟ ~ T 3 . Setzt man die Zah⎟ wird dann
5
5
⎝ ∂T ⎠V
⎝θ ⎠
⎝θ ⎠
3
⎛T ⎞
lenwerte ein, so erhält man für tiefe Temperaturen CV = 464,3 J mol ⋅ K ⎜ ⎟ .
⎝θ ⎠
Es ist bemerkenswert, dass in den Formeln für U und CV schlussendlich nur noch ein
materialabhängiger Parameter auftritt, nämlich θ (bzw. θ/T). Somit ist eine Auftragung
von CV N über T für alle Materialien gleich! [Bild 10] [Tab. 1]
θ
3V k
Da θ ~ ωmax = 2
α
(siehe Abschnitt 2) ist die Debye-Temperatur θ groß bei kleiner
m
Atommasse m und großer Federkonstante α (d.h. hoher Schmelzpunkt). Diese Debye-Theorie besticht durch die Beschreibung der Wärmeleitfähigkeit unterschiedlicher Materialien, ist aber immer noch nicht realitätsgetreu: Wir wissen bereits aus
den Abschnitten 2 und 3, dass die Schallgeschwindigkeit v0 nicht linear mit k skaliert,
sondern als Funktion v0(k) aufgefasst werden muss (Dispersionsbeziehung!).
10. Spezifische Wärme von Metallen
Auch freie Elektronen haben eine spezifische Wärme: CV = CVphonon + CVelektron . Allerdings kommen nut in Metallen freie Elektronen in hoher Konzentration vor. Und auch
hier tragen nur diejenigen Elektronen zur spezifischen Wärme bei, die von einem auf
einen anderen Zustand wechseln können. Das ist nur in einem Bereich von ca. 3kT
um die Fermi-Energie EF herum möglich (hier sind zwischen 20% und 80% der Zustände besetzt, siehe Halbleiter-Skript). Somit ist der Anteil der Elektronen, die zur
3 kT
3 kT
spezifischen Wärme beitragen,
(vgl. Dulong-Petit).
, und CVelektron = 3 R
2 EF
2 EF
Eine genaue Integralrechnung liefert CVelektron =
π2
2
R
kT
. Der Anteil der spezifischen
EF
Wärme, der durch Elektronen vermittelt wird steigt also (für niedrige Temperaturen)
linear mit T, derjenige der Phononen mit T³. Rechnungen zeigen, dass nur für sehr
geringe Temperaturen (unterhalb 1–3 K) der elektronische Anteil dominiert. [Bild 11]
11. Wärmeleitfähigkeit
Die Wärmeleitung in Nichtmetallen erfolgt über Gitterschwingungen, also "Stöße mit
den nächsten Nachbarn". Photonen können dabei als "Teilchen" mit Energie und Impuls aufgefasst werden, die mit anderen Teilchen kollidieren. Je größer die freie
Weglänge der Photonen, desto höher die Wärmeleitfähigkeit λ. Die freie Weglänge Λ
wird bei tiefen Temperaturen vorwiegend durch Stöße an Störstellen, bei hohen
Temperaturen durch Stöße an anderen Phononen begrenzt. So entsteht typischerweise ein Maximum der Wärmeleitfähigkeit im Bereich 30–300 K und ein Verlauf mit
λ ~ T–1 bei hohen Temperaturen. Eine starke Schädigung des Gitters oder eine hohe
Störstellenkonzentration bewirkt einen drastischen Abfall der Wärmeleitfähigkeit auch
bei hohen Temperaturen. Auch die Isotopenreinheit spielt eine Rolle. [Bild 12]
In Metallen ist die Wärmeenergie ebenfalls in Gitterschwingungen gespeichert. Bei
nicht zu tiefen Temperaturen wechselwirken die freien Elektronen mit den Phononen;
das Elektronengas wird aufgeheizt. Die Wärmeleitung erfolgt damit hauptsächlich
über Elektronen. Es besteht ein direkter Zusammenhang zwischen der freien Weglänge der Elektronen (und damit der elektrischen Leitfähigkeit, siehe Skript) und der
Wärmeleitfähigkeit. Dies kommt im Wiedemann-Franz-Gesetz zum Ausdruck:
2
λ
π 2k 2
−8 V
= L ⋅ T mit L =
=
2
,
45
⋅
10
(Lorenzzahl).
σ
3e2
K2
12. Bilder
a’
a
Bild 1: Einatomige Kette mit longitudinaler Anregung der Wellenlänge λ = 10a.
Bild 2: Zwei Wellen mit Δλ = 2na beschreiben die gleiche Auslenkung.
Bild 4: Lineare zweiatomige Kette.
Bild 3: Dispersionsfunktion ω(k) der einatomigen linearen Kette.
Bild 5: Optische und akustische
Anregungen.
Bild 6: Dispersionsfunktion ω(k) der zweiatomigen linearen Kette.
Bild 7: Dispersionsfunktionen von Phononen in Silizium entlang verschiedener Ausbreitungsrichtungen k. Die Richtungen lassen sich im reziproken Raum an der Brillouinzone des Diamantgitters (links) verfolgen. Si besitzt auch optische Zweige, da
die Elementarzelle mehr als ein Atom enthält; die transversalen Wellen sind entartet.
Bild 8: Temperaturabhängiger verlauf der Spezifischen Wärme von Si und Ge.
Bild 9: Tatsächliche Zustandsdichte der
Phononen in Si und Vergleich mit dem
Debye-Modell.
Kristall
Cs
Hg
Pb
In
Au
KCl
Ag
Pt
Nb
ZnS
NaCl
Cu
Li
Ge
θ [K]
38
72
105
108
165
235
226
240
275
315
321
343
344
370
Kristall
W
Mg
Graphit
LiCl
Al
Mo
Ni
Fe
Cr
Si
LiF
AlN
Be
Diamant
Bild 10: Debye-Plot. Alle Kristalle haben den gleichen Verlauf von CV(T),
nur die Werte für θ unterscheiden sich.
θ [K]
400
405
420
422
428
450
450
467
630
640
732
950
1440
2230
Tab. 1: Debye-Temperaturen θ
verschiedener Werkstoffe.
Bild 11: Elektronische und phononische AnTeile an der spez. Wärme von Metallen.
Bild 12: Temperaturabhängigkeit der Wärmeleitfähigkeit für Silizium und Germanium.
Bei Silizium ist außerdem der Einfluss der Gitterdefekte, bei Germanium der Einfluss
der Isotopenreinheit dargestellt.