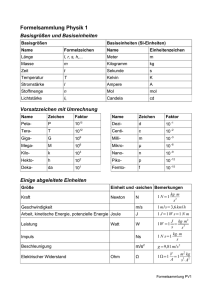
Formelzettel_fuer_Klausur - S-Inf

Einheiten
F Newton
1N=
Energie
W Joule
1 J =1 Nm=Ws
= A⋅V⋅s
Leistung
P Watt
1W =1
Ladung
Q Coulomb
Spannung
U Volt
1C =1 As

1V =1
A
Widerstand
R Ohm
1=1
Piko
p
10−12
Milli
m
10
Nano
n
10
−9
Centi
c
Mikro

10
−6
Dezi
d
Nm
s
Leitwert
G Siemes
1 S =1
A
V
Kapazität
C Farad
1 F=1
As
V
Induktivität
L Henry
1 H =1
Vs
A
magn. Fluß
 Weber
1Wb=1 Vs
magn. Indukt. B Tesla
1T =1
Vs
2
m
Frequenz
f
1 Hz=
1
s
−3
Tera
T
10
12
Kilo
k
10
10
−2
Giga
G
10
9
Hekto h
10
2
10
−1
Mega
M
10
6
Deka
10
1
Hertz
da
3
t
1
U2
2
W
=
U =R⋅I , R= , W =U⋅I⋅t , P=I ⋅R= =U⋅I ,
el ∫ P t dt
G
R
0
 er
Q⋅
−12 As
−19
 =Q⋅
 
E=
E , Punktladung: 
, F
, Kraft zw. 2 Punkten:
e=−1,602⋅10 C ,  0=8,85⋅10
Vm
4⋅⋅0⋅r
Q ⋅Q
 =Q2⋅E1= 1 ⋅ 1 2⋅
F
e r , Kirchoff: Knoten: j v j⋅I j=0 , abfließend: v j =−1 ;
4⋅⋅0 r 2
l
Maschen: j v j⋅U j=0 , entgegengesetzt: v j =−1 spez. Widerstand  : R=⋅ ;
A
N⋅A
Induktivität: L=
l
 =0⋅r⋅E
 ; C= Q = ⋅A ( A Fläche, d Abstand); E= U (Feldstärke im
el. Flussdichte: D
U
d
d
Zw.raum); Ladung auf Kondensator bleibt, wenn Spannung abgetrennt wird; Zylinderkond.:
2⋅⋅⋅l
1
1
C=
=∑
Q ges=∑ Q i ⇒ C ges=∑ C i , Reihe: U ges =∑ U i ⇒
;
Parallel:
ln r a /r i 
C ges
C i ; Arbeit bei Kond.:
C Q
C 2
W = ⋅U ; Ladung verteilt sich auf Kond. gemäß ihrer Kapazität: 2 = 2 ; Zylinderkond. mit
2
C1 Q1
2⋅⋅0⋅l
untersch. Dielektrizität: C=
ln r 1 /r i /1ln r a /r 1 /2
komplexe Zahlen
Basics
V
A
Kondensator
Potenzen
kg m
2
s
Kraft
z =x j⋅y ; z =r⋅cos  j⋅sin  mit r = x 2  y 2 und =arctan
x
; Exponentialform: z =r⋅e j⋅
y
U
I
, Leitwert: Y =
Ohmscher Widerstand:
I
U
U
1
1 − j90 °
1
j0 °
=
⋅e
Z R=R=R⋅e , Y R= , I R t = max⋅sin⋅t  ; Kapazität: Z c =
,
R
j⋅⋅C  C
R
U
I C t=C⋅U max⋅⋅cos ⋅t ; Induktivität: Z L = j⋅⋅C= L⋅e j90° , I L t=− max⋅⋅cos ⋅t ;  :
L
2
=2⋅ f , f : Frequenz Kirchhoff'sche Gesetze gelten; Regeln: 1)
Winkelgeschw.; =
T
Z 1⋅Z 2
z
z
1
x− j⋅y
1
−j
=
, 2) x j⋅y = 2 2 , 3) x j⋅y = 2 2 , 4) Z 1∥Z 2 ⇒
j⋅y y
Z 1Z 2
x y
x y
Ua
Amplitudengang: A=∣ H ∣=
, Phasengang: t =−arctan ℑ Z  ; Resonanz in
Ue
z 1⋅z 2=r 1⋅r 2⋅e
j⋅1  2
; Widerstand: Z =
∣
∣ ∣
∣
!
komplexer Schaltung: ℑ Z =0
=0 ⇒ Spule wird Kurzschluss, Kondensator Unterbrechung, =∞⇒ genau umgekehrt
1
1
⋅U max bzw.
⋅I max ; Blindwiderstand: Im{ Z }; Wirkwiderstand: Re{ Z };
Grenzfrequenz:
2
2
Scheinwiderstand: ∣Z∣
Im{Z}>0
Im{Z}<0
Widerstände
„In Induktivitäten tun Ströme sich verspäten.“
in Reihe: U ges =∑ U i , I =const. , R ges=∑ R j Spannungsteiler:
Uj
Rj
U j Rj
=
=
,
U ges R ges U k Rk
R1⋅R 2
1
1
parallel: I ges =∑ I i , U =const. , G ges=∑ G i , R =∑ R (Sonderfall 2 Widerst.: R ges=
)
R1R 2
ges
i
I j Rges
I j Rk
R2
=
=
Stromteiler:
,
(Sonderfall 2 Widerst.: I 1=I ges⋅
)
I ges R j
Ik R j
R1R 2

magn. Durchflutung: =N⋅I ( N Anzahl Stromschleifen), magn. Feldstärke: H = l ( l m
Kochrezepte
Magnetismus
m
1
mittlere Feldlinienlänge im Eisenkern), N =1 : H =
; magn. Flussdichte: B=0⋅r⋅H ;
2 ⋅r
−7 Vs
magn. Feldkonstante: 0=4⋅10
; magn. Fluss  m :  m=B⋅A⋅cos  Induktivität:
Am
N 2⋅A
 bei geraden stromdurchflossenen Leitern:
L=0⋅r⋅
, A Querschnitt, Richtung von H
lm
I
 =H cos  ex sin  ey  , F
 =I  l x 
Rechte-Hand; H =
, H
B ; magn. Fluss:
2⋅⋅r
l




=∫ B d A=cos  A , B ⋅ ∫ Bh dx (wobei A=l⋅h ); induzierte Spannung in Spule: U i t=−n d 
A
dt
x=0
(n Windungszahl der Spule)
Ersatzspannungs-/Stromquelle: Berechne Innenwiderstand (Gesamtwiderstand Ri an
Klemmen (dazu Quellen ignorieren)), Leerlaufspannung U 0 (Spannung ohne Last zwischen
Klemmen, also die am letzten Widerstand R L abfallen würde; berechne dazu R ges (an
U
Quelle!), dann I ges = R
(U Quellenspannung!), über Stromteilerregel erhält man I L an der
ges
U0
Last, dann ist U 0=I L⋅R L ; I K =
; Spannungsquelle: U 0 und Ri angeben, Stromquelle: I K
Ri
und Ri . U =U 0− Ri⋅I , I =I k −G i⋅U
MSV: z − k −1 l.u. Maschengl. 1) Strom- in Spannungs-quelle umwandeln 2) Wahl der
Maschen, virtuellen Maschenstrom einzeichnen 3) Matrix: Ri ,i=∑ R in Masche i ,
Ri , j =∑ gem. R in i , j ( − , falls I entgegengesetzt) 4) Ergebnisvektor: U i=∑ U , U
Spannungsquelle in Masche i ( − , falls U in Richtung I i ) KPV: k −1 l.u. Knotengl. 1)
1
Spannungs- in Stromquelle umwandeln 2) R in G umwandeln G= , Knoten wählen,
R
0 =0V , virtuelle Spannung U x von jedem Knoten zu 0 def. 3) Gi ,i =∑ G , die an Knoten
i grenzen, Gi , j =−∑ aller Gi zw. i und  j 4) I j= Summe der ab- ( − ) und
0
„Ventil“, Arbeitspunkt einer Diode feststellen: Diode kurzschlieflen und I K bestimmen, Diode
rausnehmen (Leerlauf) und U 0 bestimmen. I K und U 0 als Punkte auf Achsen eintragen.
Schnittpunkt der Gerade durch die Punkte mit der Kennlinie ist Arbeitspunkt. Grafisch
Diodenstrom und Diodenspannung bestimmen.
Transistor
Bipolar-T
Diode
zufließenden (  ) Ströme an  j Leistung an geg. Lastwiderstand R L :
U L U 0⋅R L 1
U0
P L=
=
⋅ =
Superpositionsprinzip: ( U oder I im Netzwerk mit mehreren
RL
R ges R L R ges
Quellen) a) Stromquelle weglassen, 1. Teilkomponente an gew. Stelle berechn. b)
Spannungsquelle weglassen, 2. Teilkomponente ab gew. Stelle berechn.; I ges =I 01 I 02
I B=
U BB – U BE
RB
ein
; I C ∣U =U =
CE
UB
RC
wichtigster
Schaltungstyp:
Emitterschalt.,
dabei ist Spannungsquelle über
einen
gemeinsamen
Anschluß-punkt
mit dem Emitter
verbund.
U B−U CE
; I B (Basisstrom): ablesen im Diagramm {U CE }×{I C } ;
IC
IC
Basisstromverstärkung B= ; U BE : ablesen im Diagramm {U BE }×{I B } ; Widerstände in QuerIB
U B – U BE
U BE
zweigen RQ1 , RQ2 : RQ1=
, RQ2=
I Q1
I Q1
Kollektorwiderstand: RC =
OP-Verstärker
Bei Maschenumläufen: Niemals durch den OPAMP durch!
Wenn + von Quelle an + von OpAmp (und - an -) dann Ausgangsspannung positiv, sonst
negativ!
R2
Ua
R2
=1
invertierender Verstärker: U a=−U e⋅ , nicht inv. Verstärker:
R1
Ue
R1
Ua
1
= v0
, wobei v 0 Gleichspannungsverstärkung
Ue
2
an Eingängen fließt kein Strom, Spannung zwischen + und -: U D =0
Mathe
Gleichspannung: =0 ; Grenzfrequenz:
∣ ∣
det  Ai 
mit Ai =A , nur dass i -te Spalte durch Ergebnisvektor ersetzt
det  A
a 2 b 3−a 3 b2
x⋅y

a × b= a 3 b 1−a 1 b3
, 
Vektorrechnung: Winkel: =arccos
∣x∣⋅∣y∣
a1 b 2−a 2 b1
Cramersche-Regel: x i=

