Angewandter Elektromagnetismus

Angewandter Elektromagnetismus - Formelsammlung
1
1.1
Elektrostatische Analyse
Seite 1 von 6
Vorlesung 1
Integralgleichungen der elektrostatischen Analyse
Folie 4,5
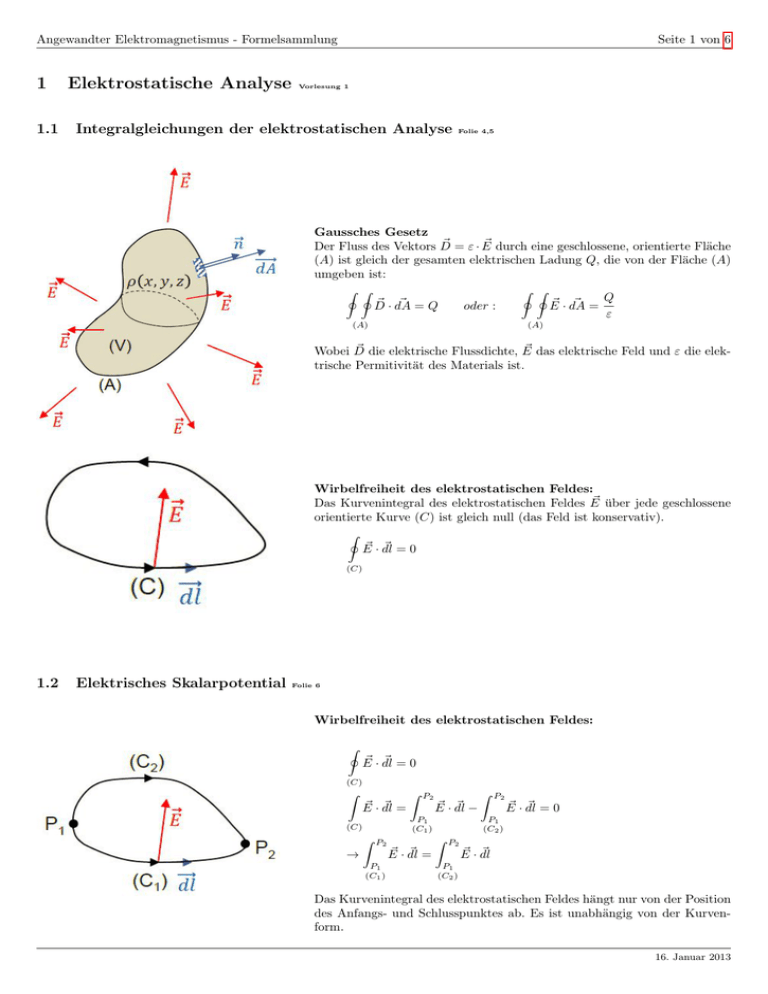
Gaussches Gesetz
~ = ε·E
~ durch eine geschlossene, orientierte Fläche
Der Fluss des Vektors D
(A) ist gleich der gesamten elektrischen Ladung Q, die von der Fläche (A)
umgeben ist:
I I
I I
~ =Q
~ =Q
~ · dA
~ · dA
D
oder :
E
ε
(A)
(A)
~ die elektrische Flussdichte, E
~ das elektrische Feld und ε die elekWobei D
trische Permitivität des Materials ist.
Wirbelfreiheit des elektrostatischen Feldes:
~ über jede geschlossene
Das Kurvenintegral des elektrostatischen Feldes E
orientierte Kurve (C) ist gleich null (das Feld ist konservativ).
I
~ =0
~ · dl
E
(C)
1.2
Elektrisches Skalarpotential
Folie 6
Wirbelfreiheit des elektrostatischen Feldes:
I
~ =0
~ · dl
E
(C)
Z
~ =
~ · dl
E
Z
P2
~ −
~ · dl
E
P1
(C1 )
(C)
Z
P2
→
P1
(C1 )
~ =
~ · dl
E
Z
P2
~ =0
~ · dl
E
P1
(C2 )
Z
P2
~
~ · dl
E
P1
(C2 )
Das Kurvenintegral des elektrostatischen Feldes hängt nur von der Position
des Anfangs- und Schlusspunktes ab. Es ist unabhängig von der Kurvenform.
16. Januar 2013
Angewandter Elektromagnetismus - Formelsammlung
Seite 2 von 6
Das elektrische Skalarpotential eines Punktes gegenüber dem Bezugspunkt
PB ):
Z
PN
ϕP1 =
~
~ · dlund
E
ϕP2 =
Z
PN
~
~ · dl
E
P2
P1
Die elektrische Spannung zwischen zwei Punkten:
Z
P2
UP1 P2 = ϕP1 − ϕP2 =
~
~ · dl
E
P1
1.3
Differenzialgleichungen der elektrostatischen Analyse
Folie 20
Laplace- und Poisson-Gleichungen:
~ =ρ
∇·D
~ =ρ
∇·E
ε
ρ
~
E = −∇ · ϕ → ∇ · ∇ϕ = −
ε
Laplace-Operator:
∇ · ∇ = ∇2 = ∆ =
∂2
∂2
∂2
+
+
∂x2
∂y 2
∂z 2
Poisson-Gleichung:
∂2
∂2
∂2
ρ
+
+
=−
∂x2
∂y 2
∂z 2
ε
Laplace-Gleichung:
∂2
∂2
∂2
+
+
=0
∂x2
∂y 2
∂z 2
Randbedingungen:
∂2ϕ
∂x2
2
2
+ ∂∂yϕ2 + ∂∂zϕ2 = 0
Der geerdete Rand: ϕ = 0, (x, y, z)Γe
Der Rand mit dem bekannten Potential: ϕ = A, (x, y, z)Γb
Der Rand der Symmetrie: ∂ϕ
∂n = 0, (x, y, z)Γs
16. Januar 2013
Angewandter Elektromagnetismus - Formelsammlung
2
2.1
Stationäre Strömungsanalyse
Seite 3 von 6
Vorlesung 2
Integralgleichungen der stationären Strömungsanalyse
Folie 4
Elektrische Stromdichte:
dI
J~ =
· ~n mA2
dA
Wobei dA eine kleine, der Stromrichtung senkrechte Fläche ist, ~n der senkrechte Einheitsvektor der Fläche dA und dI der durch die Fläche fliessende
Strom ist.
Der RR
gesamte Strom durch die lässt sich offenbar so angeben:
~
I=
J~ · dA
(A)
Kontinuitätsgleichung
Wenn (A) eine geschlossene orientierte Fläche ist, lässt sich der herausfliessende elektrische Strom so berechnen:
I I
~
I=
J~ · dA
(A)
Wegen der Erhaltung der Ladung in dem Gebiet (V ) muss dieser herausfliessende Strom gleich der Abnahme der gesamten Ladung im Volumen
(V ) sein:
ZZZ
ZZZ
dQ
d
dρ
I=−
ρ · dV = −
=−
dV
dt
dt
dt
(V )
(V )
Die Kombination dieser Gleichungen führt zu:
I I
ZZZ
dρ
~ =−
J~ · dA
dV
dt
(A)
(V )
in der stationären Strömungsanalyse hat diese Formel folgende Form:
I I
~ =0
J~ · dA
(A)
Ohmsches Gesetz:
dA
dU
= G · dU = σ ·
· dU
R
l
dA
G=σ·
l
l
R=ρ·
s
dA
J · dA = σ ·
·E·l →J =σ·E
l
dI =
~
oder in Vektorform: J~ = σ · E
16. Januar 2013
Angewandter Elektromagnetismus - Formelsammlung
3
3.1
Magnetostatische Analyse
Seite 4 von 6
Vorlesung 3
Integralgleichungen der magnetostatischen Analyse
Folie 4
Ampèresches Gesetz:
I
~ =
~ · dl
H
n
X
Ik
k=1
(C)
Weil die Stromsumme als die magnetische Durchflutung bezeichnet wird:
Θ=
n
X
Ik
k=1
Der gesamte Strom durch die Fläche (A) lässt sich als das Integral der
Stromdichte berechnen:
ZZ
n
X
~
Ik =
J~ · dA
k=1
(A)
was zu der Gleichung führt:
I
ZZ
~ =
~
~ · dl
H
J~ · dA
(C)
(A)
und mit B = µH lautet:
I
ZZ
~ = µ0
~
~ · dl
B
J~ · dA
(C)
(A)
Quellenfreiheit des Magnetfeldes:
Der magnetische Fluss durch eine geschlossene orientierte Fläche ist immer
gleich null!
I I
~ =0
~ · dA
B
(A)
Das bedeutet, dass die magnetischen Feldlinien immer geschlossen sind.
16. Januar 2013
Angewandter Elektromagnetismus - Formelsammlung
4
4.1
Seite 5 von 6
Magneto-quasistatische Analyse
Vorlesung 4
Integralgleichungen der magneto-quasistatischen Analyse
Folie 6
Faraday’sches Induktionsgesetz:
Der zeitabhängige magnetische Fluss induziert eine elektrische Spannung
in der vom durchflossenen Spule:
ui = −
∂Φm
∂t
der magnetische Fluss ist:
I I
~ wobei S die Fläche ist
~ · dS,
B
Φm =
(S)
die induzierte Spannung der Spule ist:
I
I I
~ =−∂
~
~ · dl
~ · dS
ui =
E
B
∂t
(C)
(S)
Randbedingungen:
~ = 0, (x, y, z)Γi
Magnetische Isolierung: ~n × A
Der Rand zwischen zwei Materialien: ~n × A~1 = ~n × A~2 , (x, y, z)Γs
Randwertproblem:
~
∂A
= −µ0 J~q , (x, y, z)Ω
∂t
~ = 0, (x, y, z)Γi
~n × A
~ − µ0 σ
∆A
Randwertproblem im Frequenzbereich:
~ − jωµ0 σ A
~ = −µ0 J~q , (x, y, z)Ω
∆A
~ = 0, (x, y, z)Γi
~n × A
5
5.1
Elektrodynamische Analyse (Maxwell’sche Gleichungen)
Differentialgleichungen der elektrodynamischen Analyse
Vorlesung 5
Folie 13
Faraday’sches Induktionsgesetz:
I
~ =−∂
~ · dl
E
∂t
I I
(C)
~ →∇×E
~ · dS
~ =
B
(S)
~
∂B
−
∂t}
| {z
EH−Kopplung
Ampèresches Gesetz:

I
~ = µ0
~ · dl
B
(C)
ZZ
(S)
~
∂D
J~ +
∂t
!

~ →∇×B
~ = µ0 J~ +
· dS


~
∂D
∂t
|{z}



EH−Kopplung
16. Januar 2013
Angewandter Elektromagnetismus - Formelsammlung
Maxwell’sche Gleichungen (1. Variante)
~ =ρ
∇·D
~ =0
∇·B
~
~ = − ∂B
∇×E
∂t
!
~
∂
D
~ = µ0 J~ +
∇×B
∂t
Kontinuitätsgleichung:
∂ρ
∇ · J~ =
∂t
Wellengleichung H-Feld:
2~
~
~ − µσ ∂ H − µε ∂ H
∆H
∂t
∂t2
6
6.1
Seite 6 von 6
Maxwell’sche Gleichungen (2. Variante)
~ =ρ
∇·E
ε
~ =0
∇·H
~
~ = −µ ∂ H
∇×E
∂t
~
~ = σE
~ + ε ∂E
∇×H
∂t
Wellengleichung E-Feld:
2~
~
~ − µσ ∂ E − µε ∂ E
∆E
∂t
∂t2
Finite Element Methode 2-D
Vorlesung 6
2-D elektrostatisches Randwertproblem
Elektrische Energie: We =
RR
1
2
ρ · ϕdS =
(Ω)
Q
U
RR
1
2
Folie 5
~ · EdS
~
D
(Ω)
Elektrische Kapazität: C =
Elektrische Energie eines Kondensators: We = 21 QU = 12 CU 2
7
7.1
Finite Element Methode 3-D
Vorlesung 8
3-D elektrostatisches Randwertproblem
Folie 4
Poisson-Gleichung:
∂2ϕ ∂2ϕ ∂2ϕ
ρ
+
+
= − , (x, y, z)Ω
2
2
2
∂x
∂y
∂z
ε
Randbedingungen:
ϕ = 0, (x, y, z)Γe
ϕ = U, (x, y, z)Γb
∂ϕ
= 0, (x, y, z)Γs
∂n
dabei ist ρ die Verteilung der Raumladungsdichte, ε die elektrische Permitivität, ϕ die unbekannte elektrische Potentailverteilung und Ω das Rechengebiet.
RRR
RRR
~ · EdV
~
Elektrische Energie: We = 21
ρ · ϕ · dV = 12
D
(Ω)
(Ω)
16. Januar 2013