ERGEBNISSE TECHNISCHE MECHANIK III-IV - mv.uni

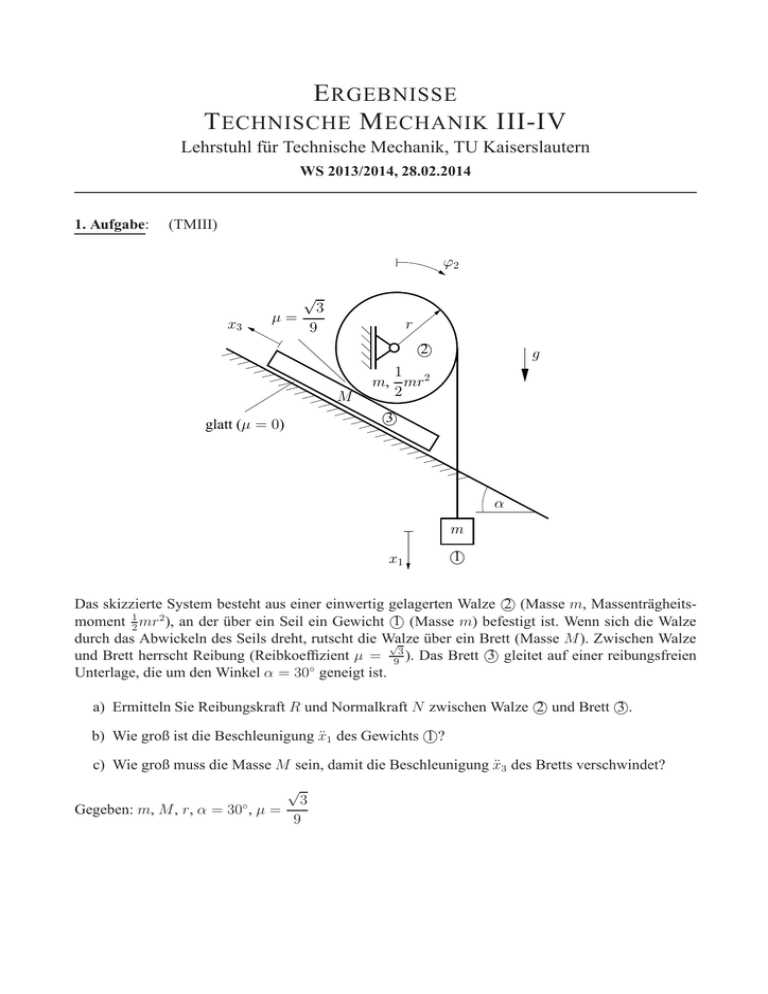
E RGEBNISSE
T ECHNISCHE M ECHANIK III-IV
Lehrstuhl für Technische Mechanik, TU Kaiserslautern
WS 2013/2014, 28.02.2014
1. Aufgabe:
(TMIII)
ϕ2
x3
√
3
µ=
9
r
2
M
glatt (µ = 0)
g
1
m, mr2
2
3
α
m
x1
1
2 (Masse m, MassenträgheitsDas skizzierte System besteht aus einer einwertig gelagerten Walze 1
2
1 (Masse m) befestigt ist. Wenn sich die Walze
moment 2 mr ), an der über ein Seil ein Gewicht durch das Abwickeln des Seils dreht, rutscht die Walze
über ein Brett (Masse M). Zwischen Walze
√
3 gleitet auf einer reibungsfreien
und Brett herrscht Reibung (Reibkoeffizient µ = 93 ). Das Brett ◦
Unterlage, die um den Winkel α = 30 geneigt ist.
2 und Brett .
3
a) Ermitteln Sie Reibungskraft R und Normalkraft N zwischen Walze 1
b) Wie groß ist die Beschleunigung ẍ1 des Gewichts ?
c) Wie groß muss die Masse M sein, damit die Beschleunigung ẍ3 des Bretts verschwindet?
√
3
Gegeben: m, M, r, α = 30◦ , µ =
9
a)
2
R = mg,
5
b)
2
ẍ1 = g
5
c)
4
M= m
5
N=
6√
3mg
5
2. Aufgabe:
(TMIII)
ϕ, ω
z
s
g
α
m
s0
In einem im Winkel α an einer rotierenden Stange befestigten Rohr gleitet eine Masse m reibungsfrei.
Die Stange rotiert zunächst mit der konstanten Winkelgeschwindigkeit ω = ω0 .
a) Wie groß muss die Winkelgeschwindigkeit ω0 sein, damit die Masse m ihre Position entlang
der Rohrachse nicht ändert (ṡ = 0, s = s0 )? Zeichnen Sie ein geeignetes Freikörperbild!
Nun soll die Masse m aus dieser Lage mit konstanter Geschwindigkeit ṡ = c0 entlang der Rohrachse
(s-Achse) bewegt werden.
b) Berechnen Sie die für diese Bewegung notwendige Winkelgeschwindigkeit ω(t) in Abhängigkeit der gegebenen Größen.
∗
Für einen
rbestimmten Winkel α und ṡ = c0 sei die Winkelgeschwindigkeit nun gegeben mit
g
.
ω(t) =
s0 + c0 t
c) Ermitteln Sie die Bahnkurve s(ϕ) der Masse m mit den Anfangsbedingungen ϕ(t = 0) = 0
und s(t = 0) = s0 .
r
3
g
d) Zeigen Sie, dass für die Zirkularbeschleunigung gilt: aϕ (t) = c0
sin(α∗ ) .
2
s0 + c0 t
Gegeben: g, s0 , c0 , m, α
a)
ω0 =
s
g cos(α)
s0 sin2 (α)
b)
ω(t) =
s
s(ϕ) =
cos(α)
g
(s0 + c0 t) sin2 (α)
c)
c0 ϕ √
√ + s0
2 g
2
3. Aufgabe:
(TMIII)
ϕ, ω
y
g
x
M
11
00
00
11
00
11
H
m
C
B
A
2a
2
m
3
δ
a
2a
Ein Artist, der idealisiert als Massenpunkt mit der Masse M angenommen wird, fällt wie skizziert aus
der Ruhe heraus aus der Höhe H auf eine Wippe mit der Masse m und der Länge 3a. Die Wippe wird
bis kurz vor dem Stoß gehalten, so dass der Massenpunkt senkrecht auf die ruhende Wippe trifft.
a) Berechnen Sie das Massenträgheitsmoment θA der Wippe bezogen auf deren Drehpunkt A.
b) Wie groß ist die Geschwindigkeit v1 des Massenpunktes M unmittelbar vor dem Stoß?
c) Betrachten Sie nun den Stoß zwischen Massenpunkt und Wippe. Der Stoß sei ideal plastisch
(e = 0). Ermitteln Sie die Stoßkraft F̂ , die Geschwindigkeit v̄1 des Massenpunktes unmittelbar
nach dem Stoß sowie die Winkelgeschwindigkeit ω̄1 der Wippe unmittelbar nach dem Stoß.
Nach dem Stoß haftet der Massenpunkt M dauerhaft an der Wippe, und die Wippe dreht sich um
einen vernachlässigbar kleinen Winkel, bis sie im Punkt B auf die abgebildete ruhende Stange mit
der Masse 32 m und der Länge 2a stößt. Die Stange ist im Punkt C drehbar gelagert.
d) Wie groß muss bei diesem zweiten Stoß die Stoßkraft F̂2 auf die Stange mindestens sein, damit
die Stange um 90◦ in die abgebildete vertikale Position rotiert?
Gegeben: a, H, m, M, g, δ ≪ a, e = 0 (erster Stoß)
a)
θA = m a2
b)
c)
p
v1 = − 2 g H
mM p
2gH
4M + m
4M p
v̄1 = −
2gH
4M + m
p
2M
2gH
ω̄1 =
(4M + m)a
F̂ =
d)
r
F̂2 = m
8
ag
27
4. Aufgabe:
(TMIV)
ud = x0 sin Ωt
m
d
ϕ
a
A
a
c
uc = x0 cos Ωt
a
3m
(Hinweis: Für die gesamte Aufgabe wird angenommen, dass die Ausschläge klein sind.)
Das skizzierte System besteht aus einem starren Balken der Masse m und einer Punktmasse der
Masse 3m. Der Balken ist im Punkt A drehbar gelagert, und hat die Länge 3a. Das System wird wie
skizziert über eine Feder (Federkonstante c) und einen Dämpfer (Dämpfungskonstante d) angeregt.
Die entsprechenden Weganregungen lauten uc = x0 cos Ωt und ud = x0 sin Ωt.
Ermitteln Sie
a) das Massenträgheitsmoment des Systems bezüglich des Punktes A,
b) die Bewegungsgleichung in Abhängigkeit von ϕ,
c) die Lösung ϕ(t) für den eingeschwungenen Zustand.
Hinweis:
sin α = √
tan α
2
1 + tan α
Gegeben: m, c, d, a, x0 , Ω
cos α = √
1
1 + tan2 α
a)
Θ = 13ma2
b)
ϕ̈ +
d
c
(c + dΩ) x0
ϕ̇ +
ϕ=
cos Ωt
13m
13m
13m a
A=
d
,
13m
c)
B=
ϕ̈ + Aϕ̇ + Bϕ = E
ϕ(t) = ϕP (t) =
tan γ =
V =p
c
,
13m
E=
x0
cos Ωt
a
x0
V cos(Ωt − γ)
a
AΩ
B − Ω2
E
(B − Ω2 )2 + A2 Ω2
c + dΩ
13m
5. Aufgabe:
(TMIV)
1
2L
A
1
2L
ϕ
m1
cT
S
B
m2
cf
M
1
3L
2
3L
x
(Hinweis: Für die gesamte Aufgabe wird angenommen, dass die Ausschläge klein sind. Lageenergien
sind zu vernachlässigen.)
Das skizzierte System besteht aus zwei starren Balken mit den Massen m1 und m2 , die jeweils an den
Punkten A und B drehbar gelagert sind. Beide Balken sind über einen Stab S miteinander verbunden
und am Gelenk A befindet sich eine Drehfeder der Steifigkeit cT . Die Masse M ist wie skizziert über
eine Feder der Steifigkeit cf mit dem Balken m2 verbunden. In der skizzierten Lage befindet sich das
System in der statischen Ruhelage.
Ermitteln Sie in Abhängigkeit von x und ϕ
a) die potentielle und die kinetische Energie des Systems,
b) die Bewegungsgleichungen,
c) das charakteristische Polynom zur Ermittlung der Eigenfrequenzen.
Für die Werte M = 1 kg, m1 = 3 kg, m2 = 0 kg, cf = 1 N/m, cT = 4 Nm, L = 2 m sind
d) die Eigenkreisfrequenzen und die Amplitudenverhältnisse der freien Schwingung zu ermitteln.
Gegeben: m1 , m2 , M, cT , cf , L
a)
1
3
1
T =
m1 + m2 L2 ϕ̇2 + M ẋ2
6
8
2
3
9
1
1
2
cT + cf L ϕ2 + cf Lxϕ + cf x2
Π=
2
8
2
2
b)
1
3
3
9
2
2
m1 + m2 L ϕ̈ + cT + cf L ϕ + cf Lx = 0
3
4
4
2
3
M ẍ + cf Lϕ + cf x = 0
2
c)
3
3
9
1
1
2 4
2
2
m1 + m2 ML ω −
m1 + m2 L cf + cT M + cf ML ω 2 + cf cT = 0
3
4
3
4
4
d)
ω1 = 2, ω2 =
Aϕ
Ax
= 1,
1
1
2
Aϕ
Ax
2
=−
1
4
6. Aufgabe:
x, u
(TMIV)
x, u
E, A, m
E, A, m
k
U0 cos(Ωt)
2l
2l
a
a)
b)
Bei System a) ist ein Stab zwischen zwei Wänden fest eingespannt. Der undeformierte Stab hat die
Länge 2l und wird durch die Einspannung um a (a ≪ l) gedehnt. Zum Zeitpunkt t = 0 löst sich der
Stab vom rechten Lager.
a) Geben Sie die Randbedingungen zum Zeitpunkt t < 0 und die Anfangsbedingungen zum Zeitpunkt t = 0 an.
Bei System b) ist ein Stab der Länge 2l auf der linken Seite fest eingespannt. Die Feder, welche am
rechten Stabende hängt, wird mit der Frequenz Ω harmonisch angeregt. Die Amplitude der Bewegung
ist durch U0 gegeben.
b) Geben Sie die Randbedingungen an.
c) Ermitteln Sie die Schwingungsgleichung für dieses System im eingeschwungenen Zustand in
Abhängigkeit der gegebenen Größen.
Gegeben: E, A, m, l, a (a ≪ l), k, U0 , Ω
a)
u(0, t) = 0
a
N(2l, t) = EA
2l
a
u(x, 0) = x
2l
u̇(x, 0) = 0
b)
u(0, t) = 0
N(2l, t) = k(U0 cos(Ωt) − u(2l, t))
c)
u(x, t) =
Ω
Ω
x + B sin
x
cos(Ωt)
A cos
c
c
A =0
B =
EA Ωc
cos
kU0
+ k sin
Ω
2l
c
Ω
2l
c
mit c2 =
2lEA
E
=
ρ
m