Versuch O1 R0

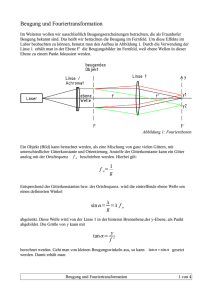
Physikalisch-technisches Messpraktikum: O1
Versuch O1: Spektrale Untersuchung von Licht
Aufgaben:
1. Ermitteln Sie unter Nutzung der bekannten Wellenlängen der Spektrallinien von Licht einer
Quecksilberdampflampe die Gitterkonstante des Ihnen vorliegenden Beugungsgitters.
2. Identifizieren Sie die Ihnen ausgehändigte unbekannte Lichtquelle unter Verwendung der im
Versuch 1 ermittelten Gitterkonstanten des Beugungsgitters.
3. Die Beugungsbilder des Lichtes eines He-Ne-Lasers, die durch Einfach-, Mehrfachspalte und
Gitter bzw. von Hindernissen (Kante, Draht) erzeugt werden, sind unter Verwendung eines
Linienschreibers aufzunehmen, mit den erwarteten Bildern zu vergleichen und hinsichtlich
der charakteristischen Kenngrößen der Hindernisse (z.B. Spaltbreite, Spaltabstand der Mehrfachspalte bzw. Gitterkonstanten) auszuwerten.
Grundlagen:
•
•
•
•
•
Das HUYGEN-FRESNELsche Prinzip der Wellenausbreitung; Kohärenz als Bedingung für Interferenzerscheinungen
FRAUNHOFERsche und FRESNELsche Beugung
Beschreibung der Beugungs- und Interferenzerscheinungen am Spalt, Doppelspalt, am Gitter
und einem Hindernis Entstehung von Intensitätsmaxima und –minima,
Entstehung des Linienspektrums durch Anregung von Gasatomen, Emission und Absorption
grundlegende Funktionsweise eines He-Ne-Lasers und eines Spektrometers
Die FRAUNHOFERsche Beugung an Ein- und Mehrfachspalten erzeugt auf einem Bildschirm in der
Entfernung e folgende normierte Intensitätsverteilung:
I ( x) =
mit δ = π
1 sin 2 δ sin 2 (N η )
N2 δ 2
sin 2 η
g sin α . Dabei ist d - die Spaltbreite, g - die Gitterkonstante (Spaltabd sin α und
η =π
λ
λ
stand), N – die Spaltanzahl, λ - die Wellenlänge des monochromatischen Lichtes und der Winkel
α - der Winkel des abgebeugten Lichtes. Um die Intensitätskurven betragsmäßig vergleichbar zu
machen, wurde der Vorfaktor 1 2 eingeführt. Der Winkel α wird durch den Abstand x des vom
N
Intensitätszentrum abgebeugten Lichtes und den Abstand e des Schirms vom Beugungsobjekt
x . Für die Abbildung 1 wurden folgende
e
Werte verwendet: λ = 623.8 nm, e = 200 mm, d = 0.02 mm, g = 0.05 mm .
(Spalt, Mehrfachspalt oder Gitter) bestimmt: tan α =
-1-
Physikalisch-technisches Messpraktikum: O1
Intensitätsverteilung bei der Beugung am Spalt
Intensitätsverteilung bei der Beugung am Doppelspalt
Intensität (a.u.)
0.80
0.40
0.00
-10
-8
-6
-4
-2
0
2
4
6
8
10
-10
-8
Abstand vom Zentrum der Intensität (mm)
-6
-4
-2
0
2
4
6
8
10
Abstand vom Zentrum der Intensität (mm)
Intensitätsverteilung bei der Beugung am Dreifachspalt
Intensitätsverteilung bei der Beugung am Vierfachspalt
Intensität (a.u.)
0.80
0.40
0.00
-10
-8
-6
-4
-2
0
2
4
6
8
10
-10
-8
-6
-4
-2
0
2
4
6
8
10
Abstand vom Zentrum der Intensität (mm)
Abstand vom Zentrum der Intensität (mm)
Intensitätsverteilung bei der Beugung am Zehnfachspalt
Intensitätsverteilung bei der Beugung am idealen Gitter (100 Spalte)
Intensität (a.u.)
0.80
0.40
0.00
-10
-8
-6
-4
-2
0
2
4
6
8
10
-10
-8
-6
-4
-2
0
2
4
6
8
10
Abstand vom Zentrum der Intensität (mm)
Abstand vom Zentrum der Intensität (mm)
Abb. 1: Intensitätsverteilung bei der Beugung an N Spalten (N = 1, 2, 3, 4, 10, 100) bei der
FRAUNHOFERschen Beobachtungsart. Die dünn eingezeichneten Linien entsprechen der Intensitätsverteilung des einfachen Spaltes.
Literatur:
Geschke, Physikalisches Praktikum:
Optik und Atomphysik
2.0
Allgemeine Grundlagen zur Interferenz, Kohärenz und Beugung
2.2
Beugung an Spalt und Doppelspalt
2.3
Beugung am Gitter
6.4
Rydberg-Konstante und Plancksches Wirkungsquantum
Stroppe, Physik:
41
Wellenoptik (Abschnitt 1, 3, 4, 6, 7)
44.1-3 Atombau und Spektren
-2-
Physikalisch-technisches Messpraktikum: O1
Walcher, Praktikum der Physik:
4.7
Beugung
Grimsehl, Lehrbuch der Physik – Band 3:
3.1.1. Kohärenz
3.2.
Beugung (3.2.1. – 3.2.4.)
6.2.
Atomhülle und Spektrum (6.2.1. und 6.2.5.)
Testfragen:
1. Wodurch unterscheiden sich FRAUNHOFER- und FRESNELsche Beugung?
2. Leiten Sie die Formeln zur Berechnung der Position der Maxima bei der Beugung am
Gitter bzw. der Position der Minima bei der Beugung am Spalt unter Verwendung entsprechender Skizzen her!
3. Was verstehen Sie unter Absorption und Emission von Licht (Bohrsches Atommodell)?
4. Nennen Sie die wichtigsten Eigenschaften von Laser-Licht!
Hinweise zur experimentellen Durchführung:
Zu 1:
Bauen Sie auf der optischen Bank mit Lichtquelle (Hg-Dampflampe), Kondensor (f = 50 mm),
Spalt und Linse (f = 100 mm) und Schirm bei sorgfältiger Justierung eine Anordnung zur Erzeugung einer scharfen Abbildung des Beleuchtungsspaltes auf den Schirm auf. (s. auch Skizze
am Arbeitsplatz)
Abb. 2: Versuchsanordnung zur Erzeugung eines Beugungsbildes des Gitters (L – Lichtquelle, K –
Kondensor, Bsp – Beleuchtungsspalt, Li – Linse, G – Gitter, S – Schirm, e – Abstand zwischen
Gitter und Schirm, an – Abstand der n-ten Beugungsordnung von der 0-ten) bei Verwendung von
Licht einer Wellenlänge.
Bringen Sie dann in den Strahlengang zwischen Linse und Schirm das auszumessende Beugungsgitter, welches ihnen vom Assistenten ausgehändigt wird. Reduzieren Sie das einfallende
Fremdlicht so weit wie möglich.
Optimieren Sie die Breite des Beleuchtungsspaltes, um einerseits ein ausreichend helles Bild
der Spektrallinien zu erhalten und damit auch schwächere Spektrallinien zu identifizieren (breiterer Beleuchtungsspalt) und andererseits ein höheres Auflösungsvermögen mit einer präzisen
Lage der einzelnen Linien zu bekommen (schmaler Beleuchtungsspalt).
Markieren Sie die Lage der Spektrallinien (pos. und negat. Ordnung, d.h. + und 1.Beugungsordnung) auf einem weißen Blatt Papier, das an den Schirm befestigt wird. Versehen
Sie das Blatt Papier vorher mit einem waagerechten Strich, um die Spektrallinien in einheitlicher
Höhenlage einzeichnen zu können. Korrigieren Sie dabei die Position der Linse für jede Spektrallinie so, dass diese möglichst scharf abgebildet wird. Versuchen Sie dabei, die beiden benach-
-3-
Physikalisch-technisches Messpraktikum: O1
barten starken gelben Linien (λ1 = 579.07 nm, λ2 = 576.96 nm) aufzulösen, d.h. auf dem
Schirm voneinander zu unterscheiden. Notieren Sie sich zu jeder Spektrallinie die Farbe und
die subjektiv empfundene Intensität der Spektrallinien (vgl. Sie mit den Angaben in der Tabelle
im Anhang!).
Messen Sie den Abstand e zwischen Gitter und Schirm mittels der Skala an der optischen Bank.
Zu 2:
Ersetzen Sie die Quecksilber-Spektrallampe durch die vom Betreuer ausgegebene Spektrallampe
unbekannter Gasfüllung. Positionieren Sie die Spektrallampe und den Kondensor so, dass ein
Maximum an Lichtintensität auf den Spalt fällt!
Markieren Sie die Lage der Spektrallinien auf einem Blatt Papier analog zu erstens.
Notieren Sie auch hier neben der Farbe der registrierten Spektrallinien die subjektiven Intensitäten.
Richten Sie für die Spektral-Lampe den Abstand e so ein, dass die äußeren Linien der ersten
Beugungsordnung möglichst weit außen auf dem Schirm abgebildet werden.
Zu 3:
Machen Sie sich mit der Gebrauchsanweisung für den He-Ne-Laser und der Bedienungsanleitung für den xy-Schreiber vertraut.
Unter Beachtung der Sicherheitsbestimmungen für den Umgang mit Laserstrahlung ist das
Beugungsspektrum von 2 verschiedenen Beugungsobjekten durch Licht des He-Ne-Lasers mit
der Wellenlänge λ = 0.6328 µm auf einem Schirm zu erzeugen (Nicht in den Laser schauen!).
Die Funktion des Schirmes übernimmt ein xy-Schreiber, wobei der Laser so justiert wird, dass
das Beugungsbild auf das Fotoelement fällt, das auf dem Schreibschlitten des Schreibers montiert und mit dem Eingang für die y-Auslenkung verbunden ist. Korrigieren Sie gegebenenfalls
die Höhe und Ausrichtung des Schreibers oder der optischen Bank, auf der der Laser montiert
ist.
Stellen Sie für jedes Beugungsobjekt die y-Empfindlichkeit des Linienschreibers so ein, dass sich
das erste und die höheren Beugungsmaxima messbar gegenüber dem Untergrund abheben.
Dabei kann das ungebeugten Licht (Maximum 0-ter Ordnung) den Vollausschlages des Schreibers durchaus geringfügig überschreiten. (Machen Sie eventuell zwei Aufnahmen für ein Beugungsobjekt mit unterschiedlicher y-Empfindlichkeit!)
Tasten Sie zunächst das Beugungsspektrum zur Kontrolle ohne Absenkung der Schreibvorrichtung und mit höherer Schreibgeschwindigkeit ab. Bei erfolgreich durchgeführtem Probelauf
wird dann das Spektrum mit geringerer Schreibgeschwindigkeit aufgezeichnet. Es ist darauf zu
achten, dass auf das Fotoelement möglichst wenig Fremdlicht einfällt.
Verwenden Sie sowohl beim Testlauf als auch bei der Aufnahme des Beugungsbildes die zweite
Leistungsstufe des Lasers, indem Sie den Auslöser am Laser für die Zeit der Aufnahme gedrückt
halten bzw. feststellen.
Wählen Sie für die Aufnahmen von den folgenden Beugungsobjekten 2 verschiedene aus:
einfacher Spalt,
Doppelspalt,
Gitter
Haar
Messen Sie den Abstand e zwischen Beugungsobjekt und Fotoelement (5-mal messen!).
-4-
Physikalisch-technisches Messpraktikum: O1
Hinweise zur Auswertung der Messergebnisse:
Zu 1:
Für die jeweilige Wellenlänge λ einer Spektrallinie ergibt sich der Abstand des ersten Beugungsmaximums a1 von der 0.ten Ordnung aus folgenden Formeln: a1 = tan α1 , λ = g ⋅ sin α1 ,
e
sodass sich die Gitterkonstante mit
g=
λ
a 

sin  arctan 1 
e

berechnen lässt.
Die Wellenlängen der Spektrallinien einiger Spektral-Lampen sind der beiliegenden Tabelle zu
entnehmen. Ordnen Sie die registrierten Spektrallinien denen in der Tabelle zu. Verwenden Sie
zur Berechnung der Gitterkonstanten möglichst alle Spektrallinien, die Sie richtig zuordnen
konnten und bilden Sie für die Berechnung des wahrscheinlichsten Wertes für die Gitterkonstante den Mittelwert aus den Gitterkonstanten aller registrierten Spektrallinien.
Berechnen Sie die statistische Messunsicherheit der Gitterkonstante im 95%-igen Vertrauensniveau. Geben Sie die Gitterkonstante unter Berücksichtigung der Messunsicherheiten an!
Zu 2:
Berechnen Sie die Wellenlängen der beobachteten Spektrallinien unter Verwendung der in erstens berechneten Gitterkonstanten.
Versuchen Sie, durch Vergleich mit den im Anhang aufgeführten Tabellenwerten der Spektrallinien die Atomart der Gasfüllung zu identifizieren.
Stellen Sie dabei die Messwerte für a1, die daraus berechneten Wellenlängen, die zugeordneten
Tabellenwerte der Wellenlängen im Anhang sowie die Differenz zwischen den berechneten Wellenlängen und den Tabellenwerten in Form einer Tabelle gegenüber. Diskutieren Sie die Ursachen für eventuelle Abweichungen zwischen den tabellarischen und berechneten Wellenlängen.
Zu 3:
Berechnen Sie den Mittelwert des Abstandes e (Beugungsobjekt – Fotoelement).
Ermitteln Sie aus den aufgezeichneten Beugungsbildern die das jeweilige Beugungsbild charakterisierenden Abstände der Beugungsordnungen. Es wird empfohlen, zur Ermittlung der jeweils
benötigten Beugungsordnung, den Abstand zwischen der entsprechenden positiven und negativen Ordnung zu ermitteln und durch zwei zu teilen, um den Abstand zur 0. Ordnung zu ermitteln.
Für die einzelnen Beugungsobjekte wird folgendes Vorgehen empfohlen:
1. Einfachspalt:
Gesuchte Größe: Spaltbreite
Der Abstand aν des ν-ten (ν
ν = 1,2,3,…) Minimums vom Zentrum maximaler Intensität wird bei
kleinem Beugungswinkel durch folgende Formel bestimmt:
ν⋅
wobei mit λ
λ
d
= sin αν ≈
aν
e
⇒ d≈
ν ⋅λ ⋅e
aν
= 0.6328 µm die Wellenlänge des He-Ne Lasers gegeben ist, e der von Ihnen zu be-
stimmende Abstand vom Spalt zur Bildebene, d die Spaltbreite und αν der entsprechende Beugungswinkel zur nullten Beugungsordnung darstellen.
Messen Sie am besten den Abstand zwischen dem + und - ν-ten Beugungsminimum und halbieren diesen für die Ermittlung von aν. Gehen Sie nur soweit in der Auswertung, wie ein Minimum noch klar erkennbar und auswertbar ist!
2.
Doppelspalt:
Gesuchte Größe: Spaltabstand
Zur Ermittlung des Spaltabstandes g vom Mehrfachspalt nutzen Sie die Lage des Minimums
einer höheren Ordnung des Beugungsbildes, sofern diese präzise genug zu ermitteln ist (s. Ab-
-5-
Physikalisch-technisches Messpraktikum: O1
bildung 1b). Der Abstand des ν -ten (ν
= 1,2,... )
Minimums vom Zentrum der nullten Beu-
gungsordnung wird durch
(2ν − 1) λ = 2 g sin αν
≈ 2g
aν
e
⇒
g≈
( 2ν − 1) λ ⋅ e
2 aν
bestimmt. Seien Sie dabei sehr sorgfältig beim Durchzählen der Minima! Gehen Sie wie bei erstens vor (halbe Differenz zwischen + und -).
3.
Gitter:
Gesuchte Größe: Gitterkonstante
Mit der Erhöhung der Anzahl der Spalte werden die Maxima zunehmend schmaler. Somit bietet sich zur Bestimmung der Gitterkonstanten die Lage des ν -ten ausgeprägten Maximums an
(s. Abbildung 1c-f):
ν ⋅ λ = g sin αν ≈ g
4.
aν
e
⇒
g=
ν λ ⋅e
aν
Hindernis (Haar):
Gesuchte Größe: Breite des Hindernisses d
Das Beugungsbild eines Hindernisses (Haar) ist im wesentlichen identisch zu dem eines Spaltes gleicher Breite d (Babinetsche Theorem). Infolgedessen kann zur Berechnung der Haardicke
die Formel von erstens verwendet werden.
Welche Ursachen könnten zu Abweichungen der gemessenen von den erwarteten Beugungsbildern führen?
Versuchszubehör:
-
Optische Bank
Vorschaltdrossel
Spektrallampen
He-Ne-Laser
Kondensorlinse
Abbildungslinse
Spaltblende
Beugungs-Spalte und Mehrfachspalte, Hindernis
Beugungsgitter
Projektionsschirm
xy-Schreiber mit Fotoelement
-6-
Physikalisch-technisches Messpraktikum: O1
Anhang:
Element
1H
2He
3Li
11Na
19K
30Zn
48Cd
80Hg
Spektrallinien einiger Elemente (Ein- und Zweielektronenatome)
λ/nm
656.28
486.13
434.05
410.17
667.82
587.56
501.57
447.15
388.86
670.78
610.36
460.29
615.42
589.00
769.90
766.49
404.41
636.24
518.20
481.05
472.22
468.01
462.98
643.85
508.58
479.99
467.82
441.46
361.29
579.07
576.96
546.07
491.60
435.84
404.66
365.48
/ 504.77
/ 616.08
/ 589.59
/ 404.72
/ 407.78
/ 366.33
Farbe
Rot
Blaugrün
Violett
Violett
Rot
Gelb
Grün
Blau
Violett
Rot
Gelbrot
Blau
Gelbrot
Gelb
Dunkelrot
Dunkelrot
Violett
Rot
Grün
Blaugrün
Blau
Blau
Blau
Rot
Grün
Blaugrün
Blau
Blau
(Ultra-)Violett
Gelb
Gelb
Grün
Blaugrün
Blau
Violett
(Ultra-)Violett
Helligkeit
stark
mittel
schwach
schwach
stark
sehr stark
mittel
mittel
mittel
stark
mittel
schwach
schwach
stark
stark
stark
mittel
stark
mittel
stark
stark
stark
schwach
stark
stark
stark
stark
mittel
schwach
sehr stark
sehr stark
stark
schwach
stark
mittel
mittel
Sind mehrere Spektrallinien auf einer Zeile aufgeführt, sind diese mit unseren experimentellen
Mitteln nicht als einzelne Spektrallinien erkennbar, d.h. auflösbar.
Nordhausen, d. 01.03.11
-7-