Beugung und Fouriertransformation

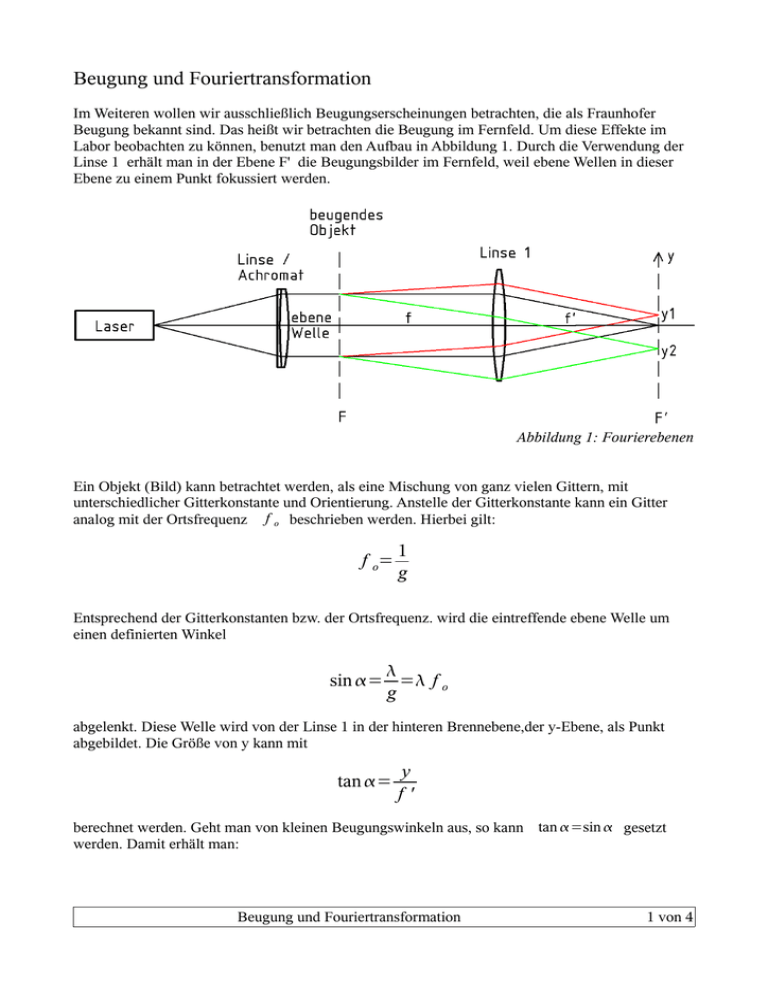
Beugung und Fouriertransformation
Im Weiteren wollen wir ausschließlich Beugungserscheinungen betrachten, die als Fraunhofer
Beugung bekannt sind. Das heißt wir betrachten die Beugung im Fernfeld. Um diese Effekte im
Labor beobachten zu können, benutzt man den Aufbau in Abbildung 1. Durch die Verwendung der
Linse 1 erhält man in der Ebene F' die Beugungsbilder im Fernfeld, weil ebene Wellen in dieser
Ebene zu einem Punkt fokussiert werden.
Abbildung 1: Fourierebenen
Ein Objekt (Bild) kann betrachtet werden, als eine Mischung von ganz vielen Gittern, mit
unterschiedlicher Gitterkonstante und Orientierung. Anstelle der Gitterkonstante kann ein Gitter
analog mit der Ortsfrequenz f o beschrieben werden. Hierbei gilt:
f o=
1
g
Entsprechend der Gitterkonstanten bzw. der Ortsfrequenz. wird die eintreffende ebene Welle um
einen definierten Winkel

sin = = f o
g
abgelenkt. Diese Welle wird von der Linse 1 in der hinteren Brennebene,der y-Ebene, als Punkt
abgebildet. Die Größe von y kann mit
tan =
y
f'
berechnet werden. Geht man von kleinen Beugungswinkeln aus, so kann tan =sin  gesetzt
werden. Damit erhält man:
Beugung und Fouriertransformation
1 von 4
y=
f'
= f ' f o
g
Leicht kann man erkennen, dass in der y-Ebene durch F' für unterschiedliche Gitter im Objekt die
entsprechenden Punkte erzeugt werden. Je größer die Ortsfrequenz ist desto größer ist die
Entfernung des dazugehörenden Punktes von der optischen Achse. Das bedeutet, einzelne Punkte
in der Ebene durch F', repräsentieren eine Frequenz in der Vorlage (Bild). Diesen mathematischen
Zusammenhang beschreibt die Fouriertransformation. Aus diesem Grund nennt man die Ebene
durch F' auch die Fourierebene, weil in dieser Ebene die Aplitudenverteilung des Lichtes der
Fouriertransformierten der beugenden Öffnung entspricht. Da wir nur Intensitäten sehen können,
entsprechen die beobachtbaren Beugungsfiguren den Quadraten der Fouriertransformierten.
Hier soll nicht die Theorie der Fouriertransformation erläutert werden, aber zum besseren
Verständnis sollen die Zusammenhänge zwischen dem Objekt und der dazugehörenden
Beugungsfigur, bzw. Funktion und Fouriertransformierte anschaulich dargestellt werden.
In der nachfolgendeen Tabelle sind für verschiedene beugende Objekte die Beugungsfiguren
(Fouriertransformormierten) dargestellt.
Beugung und Fouriertransformation
2 von 4
Beugende Öffnung
Transmission
Beugungsfigur
1,2
1,2
1
1
0,8
0,8
0,6
0,6
0,4
0,4
0,2
0,2
0
-2000
Spalt (schmal)
-1000
0
1000
2000
0
-600
I =I 0 sinc 2 
-400
-200
0
Spaltbild
Beugungsfigur
1,2
1,2
1
1
0,8
0,8
0,6
0,6
0,4
0,4
0,2
0,2
0
-2000
200
400
600
3D Plot
I =I 0 sinc 2 
b x

f'
0
-1000
0
1000
2000
Spalt: b= 500 µm
1,2
-600
-400
-200
0
200
400
600
Nullstelle: N1=526 µm
4,5
4
1
3,5
2
2,5
0,6
2
I =4 I 0 sinc cos 
3
0,8
Doppelspalt
b x

f'
Nullstelle: N1=263 µm
Spalt: b=1000 µm
Spalt (breit)
Formel
2
1,5
0,4
0,5
0
-4000 -3000 -2000 -1000
0
1000 2000 3000 4000
0
-600
b x
f'
d x
=
f'
=
1
0,2
-400
-200
0
Modulation:
Doppelspalt:
b=1000µm; d=5000 µm g=26,3 µm
200
400
600
1,2
1
0,8
Gitter
0,6
0,4
0,2
0
Transmission Gitter
Gitter
Beugung und Fouriertransformation
Beugung Gitter
3 von 4
Kreisblende Airy-Scheibchen
Nullstelle: N1=321 µm
Durchmesser: 1000µm
1,2
1,200
1
1,000
0,8
0,800
0,6
0,600
0,4
0,400
0,2
0,200
0
-2000

2J 1 
I =I 0

=
2

Dr
f
0,000
-1000
0
1000
Trnsmission Blende
2000
-600 -400 -200
0
200
400
600
Schnitt Airy-Sch.
Tabelle 1: Beugungsfiguren / Fouriertransformierte
I
Intensität in der Beobachtungsebene
I0
Maximale Intensität der Beugugsfigur auf 1 normiert

Wellenlänge des verwendeten Lichtes: hier 658 nm
f'
Brennweite der Linse: hier 400 mm
x
Koordinate in der Fourierebene; hier alle Angaben in µm
r
Abstand in der Fourierebene von der optischen Achse
b
Breite des Spaltes
Nullstelle
Abstand vom Mittenmaximum bis zur ersten Nullstelle
d
Abstand der Spalte beim Doppelspalt (Mitte zu Mitte)
Modulation
Gitterkonstante in der Beugungsfigur beim Doppelspalt
D
Durchmesser der Kreisblende
Man erkennt, dass die Beugungsfigur bei kleiner werdender beugender Öffnung breiter wird (Spalt
breit / schmal).
Beim Doppelspalt bezieht sich I0 auf die maximale Intesität eins einzelnen Spaltes. Deshalb wird
hier die Intensität maximal 4. Die eigentliche Beugungsfigur beim Doppelspalt ist rot dargestellt,
die blaue Kurve stellt die einhüllende Kurve des Einfachspaltes dar.
Benutzt man ein Gitter als beugendes Objekt, so erhält man in der Fourierebene mehrere Punkte,
die den einzelnen Beugungsordnungen des Gitters entsprechen.
Bei der Beugung an der Kreisblende erkennt man, dass die Nullstelle im Vergleich zu Einfachspalt
um den Faktor 1,22 größer ist, obwohl die der Durchmesser der Kreisblende und die Breite des
Spaltes exakt gleich sind. Weiter sieht man, dass die Nebenmaxima bei der Beugung an der
Kreisblende deutlich kleiner sind verglichen mit dem Spalt.
Beugung und Fouriertransformation
4 von 4