R2 R1 Ri L1 L2 l U0 U1

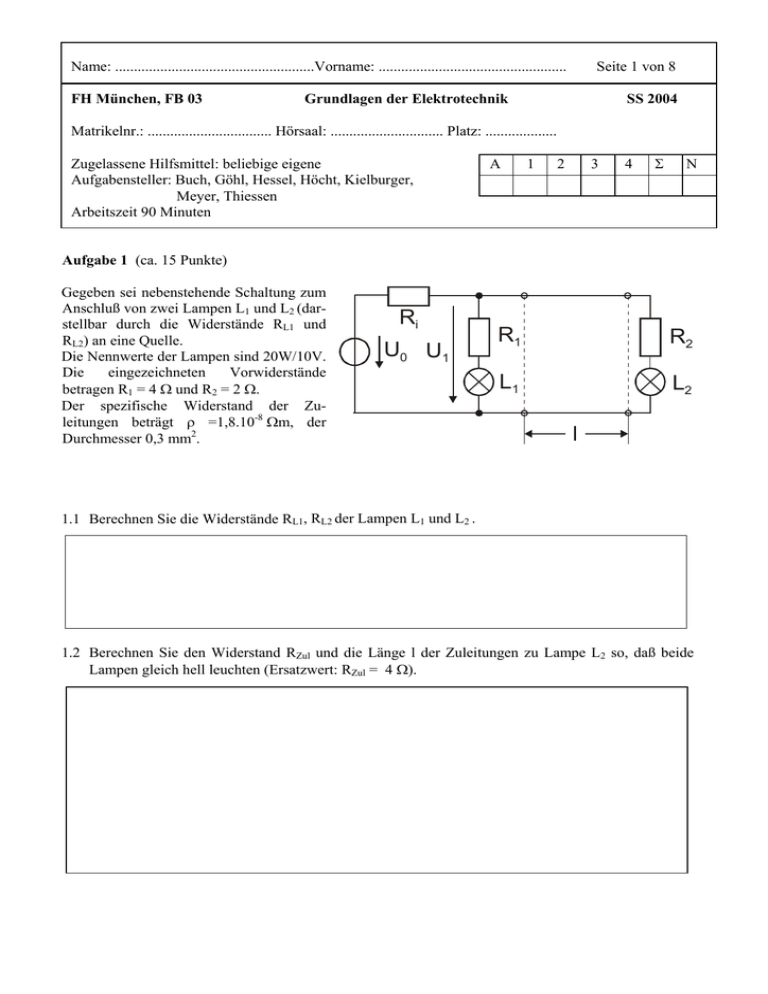
Name: .....................................................Vorname: ..................................................
FH München, FB 03
Seite 1 von 8
Grundlagen der Elektrotechnik
SS 2004
Matrikelnr.: ................................. Hörsaal: .............................. Platz: ...................
Zugelassene Hilfsmittel: beliebige eigene
Aufgabensteller: Buch, Göhl, Hessel, Höcht, Kielburger,
Meyer, Thiessen
Arbeitszeit 90 Minuten
A
1
2
3
4
Σ
N
Aufgabe 1 (ca. 15 Punkte)
Gegeben sei nebenstehende Schaltung zum
Anschluß von zwei Lampen L1 und L2 (darstellbar durch die Widerstände RL1 und
RL2) an eine Quelle.
Die Nennwerte der Lampen sind 20W/10V.
Die
eingezeichneten
Vorwiderstände
betragen R1 = 4 Ω und R2 = 2 Ω.
Der spezifische Widerstand der Zuleitungen beträgt ρ =1,8.10-8 Ωm, der
Durchmesser 0,3 mm2.
Ri
U0 U1
R1
R2
L1
L2
l
1.1 Berechnen Sie die Widerstände RL1, RL2 der Lampen L1 und L2 .
1.2 Berechnen Sie den Widerstand RZul und die Länge l der Zuleitungen zu Lampe L2 so, daß beide
Lampen gleich hell leuchten (Ersatzwert: RZul = 4 Ω).
Name: .....................................................Vorname: ..................................................
Seite 2 von 8
1.3 Wie groß muß der Innenwiderstand Ri der Quelle sein, damit die Lampen der Quelle die maximale
Leistung entnehmen? Bitte geben Sie zunächst eine allgemeine Berechnung von Ri in
Abhängigkeit von R1, R2, RL1, RL2, RZul an, und setzen Sie dann die Werte ein. (Ersatzwert: Ri = 6
Ω).
1.4 Wie groß muß die Spannung U1 sein, damit die Lampe L1 bei ihrer Nennleistung betrieben wird?
1.5
Berechnen Sie die benötigte Quellenspannung U0.
1.6 Berechnen Sie die Stromdichte in den Zuleitungen zu L2.
Name: .....................................................Vorname: ..................................................
Seite 3 von 8
Aufgabe 2 (ca. 15 Punkte)
Ein verzweigter Magnetkreis gemäß angegebener Abbildung hat folgende Werte:
N = 100 ,
A1 = 3 cm 2 ,
A2 = 3 cm 2 ,
I
A3 = 6 cm 2 ,
d = 0,5 mm ,
N
φ1 = 4 ⋅ 10 −5 Vs ,
µ r → ∞ (magn. Widerstände der
Φ2
Φ1
Eisenschenkel vernachlässigbar).
A1
Φ3
A2
d
A3
2.1 Zeichnen Sie das analoge elektrische Ersatzschaltbild des magnetischen Kreises und tragen Sie die
Zählpfeile für die Durchflutung Θ = N ⋅ I und die magnetischen Flüsse φ1 , φ 2 und φ 3 in Ihre
Zeichnung ein.
2.2 Bestimmen Sie die magnetischen Widerstände
Rm,1 , Rm, 2 , Rm,3
magnetischen Gesamtwiderstand Rm , ges der Anordnung.
der Luftspalten und den
Name: .....................................................Vorname: ..................................................
Seite 4 von 8
2.3 Wie groß ist die Stromstärke I in der Spule?
2.4 Wie groß sind die magnetischen Flüsse φ 2 und φ3 ?
Nun sei die Fläche des Luftspalts A3 = 3 cm 2 (gleichgroße Fläche wie A1 und A2 !)
2.5 Wie groß muß die Länge des Luftspalts d sein, damit bei einer Stromstärke I = 5 A in der Spule der
magnetische Fluß φ 3 = 3 ⋅ 10 −5 Vs beträgt?
Name: .....................................................Vorname: ..................................................
Seite 5 von 8
Aufgabe 3 (ca. 18 Punkte)
Hinweis: Die Teilaufgaben sind zum größten Teil weitgehend unabhängig voneinander lösbar!
Gegeben sei die nebenstehende Schaltung mit der
Spannung U 0 = 14 V .
Für t < 0 sei der Schalter seit sehr langer Zeit in der
Stellung "Aus". Zum Zeitpunkt t = 0 werde der Schalter in
die Stellung "Ein" umgelegt. Die untenstehende Abbildung
zeigt den zeitlichen Verlauf der Spannung u L an der
Induktivität L und den Strom i.
3.1 Zeichnen Sie den Verlauf der
Spannung u R am Widerstand R in das nebenstehende
Diagramm ein.
i/A
3.2 Berechnen Sie den Widerstand R.
(Ersatzwert: R=10 Ω )
0.4
0.0
3.3 Wie groß ist die Zeitkonstante τ der Serienschaltung
aus R und L?
3.4 Berechnen Sie die Größe
der Induktivität L.
Aus
U0
i
uR
L
R
u L/V
0.6
0.2
R
Ein
12
i
8
uL
4
10
20
-0.2
-4
-0.4
-8
-0.6
- 12
-0.8
- 16
-1.0
- 20
-1.2
-24
-1.4
- 28
30
t/ms
uL
Name: .....................................................Vorname: ..................................................
Seite 6 von 8
3.5 Begründen Sie, warum der Strom i zum Zeitpunkt t = 0 keinen Sprung auf einen endlichen Wert
macht, sondern stetig und damit bei Null ist.
3.6 Zum Zeitpunkt t = t1 = 20ms werde der Schalter wieder auf "Aus" zurückgeschaltet.
3.6.1 Wie groß ist unmittelbar nach dem Umschalten bei
t = t1 der Strom i(t1 ) ?
3.6.2 Wie groß ist damit die Gesamtspannung u 2 R , die
an der Hintereinanderschaltung der beiden gleich
großen Widerstände insgesamt abfällt?
3.6.3 Was folgt daraus für die Spannung u L an der
Induktivität L?
3.7 Wie groß ist die Zeitkonstante τ1 beim Ausschalten
im Vergleich zur Zeitkonstante τ beim Einschalten?
3.7.1 Zeichnen Sie den zeitlichen Verlauf des Stromes i(t ) bis zum Zeitpunkt 40ms in das Diagramm
auf der vorherigen Seite ein.
3.7.2 Zeichnen Sie den zeitlichen Verlauf der Spannung u L (t ) an der Induktivität L bis zum Zeitpunkt
40ms in das Diagramm auf der vorherigen Seite ein.
3.7.3 Was würde sich am Verlauf von i und u L ändern, wenn der beim Umlegen des Schalters auf
"Aus" zugeschaltete Widerstand R um den Faktor 20 vergrößert würde?
Name: .....................................................Vorname: ..................................................
Seite 7 von 8
Aufgabe 4 (ca. 19 Punkte)
Die nebenstehende Schaltung wird mit
einer Wechselspannungsquelle betrieben.
Die folgenden Werte seien gegeben:
Z1
I
R1
L
U q = 20 V, f = 159,155 Hz ,
R1 = 138 Ω ,
R2 = 60 Ω ,
L = 54 mH ,
C = 16,66 µF .
Z2
Uq
R2
C
4.1 Berechnen Sie die komplexen Widerstände Z1 und Z2 allgemein und mit Zahlenwerten.
4.2 Berechnen Sie das komplexe Verhältnis der Klemmenspannung UKl zur Quellenspannung Uq.
UKl
Name: .....................................................Vorname: ..................................................
Seite 8 von 8
4.3 Bestimmen Sie die komplexe Wechselspannung UKl, sowie deren Betrag UKl und deren
Phasenverschiebung ϕ zur Quellenspannung. Welche der beiden Spannungen eilt voraus?
4.4 Berechnen Sie den Betrag des eingezeichneten Stroms I.
4.5 Berechnen Sie den Betrag der Scheinleistung S, die Wirkleistung P und die Blindleistung Q der
gesamten Schaltung.
4.6 Berechnen Sie die Blindleistung QL der Induktivität und die Blindleistung QC der Kapazität.
----------------- Viel Erfolg! ---------------