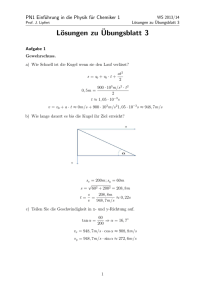
Aufgabe 1: Der Faden bleibt in der höchsten Lage der Masse

Aufgabe 1:
Der Faden bleibt in der höchsten Lage der Masse (oberer Kreispunkt) nur dann gespannt,
wenn
2
mvoben
≥ mg
r
(1)
ist. Aus der Energieerhaltung folgt
1 2
1 2
mvunten = mvoben
+ 2mgr .
2
2
(2)
Einsetzen von (1) in (2) liefert
2
vunten
> gr + 4gr
vunten ≥ vunten,min = 5gr = 8.86ms −1
Aufgabe 2:
Die Energiebilanz des Federpendels ist fehlerhaft angesetzt. Die stabile Gleichgewichtslage
entspricht dem Ort minimaler potentieller Gesamtenergie und berechnet sich damit nach
dE pot
dy
=
d 
1

−mgy + ky 2  = −mg + ky = 0

dy 
2

⇔
y=
mg
.
k
Dies ist gleichbedeutend zur Aufstellung des statischen Kräftegleichgewichts in der Ruhelage.
Die in der Aufgabenstellung suggerierte Bewegung der Masse vom Aufhängepunkt y=0 zum
Gleichgewichtspunkt, rein durch Umwandlung von potentieller Energie der Masse in
potent ielle Energie der Feder ist nicht möglich. Ein Teil der potentiellen Energie wird in
kinetische Energie umgesetzt. Ohne weitere, äußere Kräfte (Dämpfung) hat die Masse bei
y=mg/k gerade ihre maximale Geschwindigkeit.
Aufgabe 3:
a)
Energieerhaltung:
Eikin + Eipot = Efkin + Efpot
ð
1
mv 2 + 0 = 0 + mgh
2 0
;
  Θ 
h = l − l cos Θ = sl  sin   
  2 
2
2
  Θ
ð v0 = 4 gl  sin   
  2 


 v 
5m
 = 54.9°
ð Θ = 2 arcsin  0  = 2 arcsin 
2
2


2
gl


 2 9.81 ⋅ 3 m / s s 
2
r
Scheinkraft im Wagen auf Masse m: − ma
b)
Kräftegleichgewicht:
r
r
r
r
Fm = mg − ma = −FS
ð
|| Seil
a
= tan Θ
g
ð Θ = arctan
a
2
= arctan
= 11.5°
g
9.81
Aufgabe 4:
a) maximale Geschwindigkeit dann, wenn die Schwerkraft FG = m·g den Fallschirmspringer
nicht weiter beschleunigt, weil eine gleich große Reibungskraft Fr = k·v 2 entgegenwirkt:
stationäres Gleichgewicht:
⇒
kve2 = mg
⇒ ve =
mv& = ma = F = FG − Fr
v& = 0 ⇔ FG = Fr
mg
75kg ⋅ 9.81m
m
km
=
= 50,4 = 181
2
k
0.29kg s
s
h
b)
c)
d)
e)
v& :=
dv
v( t + ∆t ) − v( t )
= lim
∆
t
→
0
dt
∆t
≈
v (t + ∆t ) − v (t )
(für nicht zu große ∆t)
∆t
Einsetzen in die Bewegungsgleichung:
(
)
m(v( t + ∆t ) − v( t ) ) = mg − k (v(t ) )2 ∆t
k
ð v (t + ∆t ) = v( t ) +  g − (v (t ) )2  ∆t
m


Ausgehend von v(0) = 0 läßt sich damit v(t) für den weiteren Verlauf sukzessive
errechnen (z.B. mit ∆t = 1s):
k
v (1s ) = v( 0) +  g − (v (0) )2  ⋅ 1s = 0 + ( g − 0) ⋅1s = 9.81m / s
m


k
v (2 s ) = v(1s ) +  g − (v(1s ) )2  ⋅1s = ... = 19.23m / s
m


....
v (t + ∆t ) − v (t )
∆t
Und die Höhe h errechnet sich dann folgendermaßen:
h (t + ∆t ) = h( t ) − v (t ) ⋅ ∆t
Für die Beschleunigung a(t) gilt dann: a (t ) =
z.B.: bei einer Absprunghöhe von h(0) = 1000 m
t [s]
v [m/s]
a [m/s]
h [m]
0
0
9.81
1000
1
9.81
9.44
990
2
19.25
8.38
971
3
27.63
6.86
943
4
34.48
5.21
909
5
39.70
3.72
869
6
43.41
2.52
826
7
45.94
1.65
780
t [s]
v [m/s]
a [m/s]
h [m]
8
47.59
1.05
732
9
48.64
0.66
684
10
49.3
0.41
634
11
49.71
0.25
585
12
49.97
0.16
535
13
50.12
0.10
485
14
50.22
0.06
434
15
50.28
384
Solch eine Simulation kann man nun viel schneller mit einem Rechner durchführen. Man
wählt dazu einen möglichst kleinen Wert für ∆t. Dadurch wird die Rechnung genauer –
allerdings dauert sie dann auch länger.
„PAKMA“-Simulation zu dieser Aufgabe kann über die Internet-Seiten zur Übung
heruntergeladen und selbst verändert werden.
m/s²
10
Beschleunigung a(t)
8
6
4
2
0
0
5
10
15
Zeit t in s
60
m/s
Geschwindigkeit v(t)
40
20
0
0
5
10
15
Zeit t in s
1000
m
Höhe h(t)
800
600
400
200
0
5
10
15
Zeit t in s
Aufgabe 5: