2011b

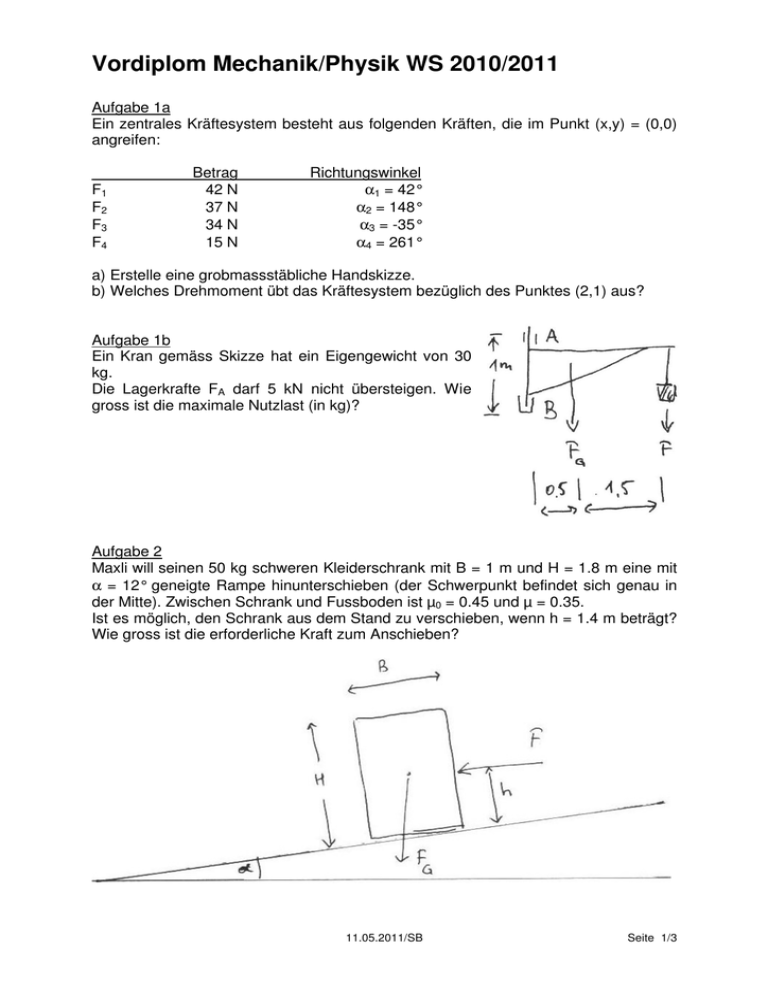
Vordiplom Mechanik/Physik WS 2010/2011
Aufgabe 1a
Ein zentrales Kräftesystem besteht aus folgenden Kräften, die im Punkt (x,y) = (0,0)
angreifen:
F1
F2
F3
F4
Betrag
42 N
37 N
34 N
15 N
Richtungswinkel
α1 = 42°
α2 = 148°
α3 = -35°
α4 = 261°
a) Erstelle eine grobmassstäbliche Handskizze.
b) Welches Drehmoment übt das Kräftesystem bezüglich des Punktes (2,1) aus?
Aufgabe 1b
Ein Kran gemäss Skizze hat ein Eigengewicht von 30
kg.
Die Lagerkrafte FA darf 5 kN nicht übersteigen. Wie
gross ist die maximale Nutzlast (in kg)?
Aufgabe 2
Maxli will seinen 50 kg schweren Kleiderschrank mit B = 1 m und H = 1.8 m eine mit
α = 12° geneigte Rampe hinunterschieben (der Schwerpunkt befindet sich genau in
der Mitte). Zwischen Schrank und Fussboden ist µ0 = 0.45 und µ = 0.35.
Ist es möglich, den Schrank aus dem Stand zu verschieben, wenn h = 1.4 m beträgt?
Wie gross ist die erforderliche Kraft zum Anschieben?
11.05.2011/SB
Seite 1/3
Vordiplom Mechanik/Physik WS 2010/2011
Aufgabe 3
r = 10 mm
b = 30 mm
c = b/3
D = 80 mm (Entfernung zur Achse)
Berechne das Gewicht des dargestellten Rotationskörpers, wenn er aus Material mit
dem spezifischen Gewicht 1.2 kg/dm³ besteht.
Aufgabe 4
Zwei Körper sind über eine masselose Schnur und eine reibungsfreie Rolle miteinander verbunden. Zur Zeit t = 0 wird die Arretierung gelöst. Wo befindet sich Körper m1
3 Sekunden später (wie viele m weiter oben oder unten auf der schiefen Ebene)?
(Annahme: die Schnur ist lang genug.)
α = 48°, β = 161°
m1 = 100 kg, m2 = 350 kg
µ1,0 = 0.32, µ1 = 0.19, µ2,0 = 0.36, µ2 = 0.21
(Die Zeichnung ist nicht massstäblich.)
11.05.2011/SB
Seite 2/3
Vordiplom Mechanik/Physik WS 2010/2011
Aufgabe 5
Ein Velofahrer wiegt 75 kg, sein Velo 10 kg. Zwischen Velo und Strasse wirkt ein
Fahrwiderstand, der wie eine Reibung mit µ = 0.06 wirkt.
a) Welche Kraft muss der Radfahrer aufbringen, um auf einer um 2% ansteigenden
Strasse die Geschwindigkeit konstant zu halten?
b) Wie gross ist der Bremsweg auf einer horizontalen Strasse bei einer Geschwindigkeit von 25 km/h, wenn die Bremse allein eine Verzögerung von 2 m/sec² bewirkt?
Aufgabe 6
Ein Auto mit Hinterradantrieb wiegt 1320 kg. Der Achsabstand beträgt 2.7 m, und der
Schwerpunkt liegt 0.90 m hinter der Vorderachse. Zwischen Reifen und Strasse betragen die Reibwerte µ0 = 0.51 und µ = 0.38. Der Raddurchmesser beträgt 63 cm.
a) Wie gross ist die maximal mögliche Beschleunigung (ausreichende Motorleistung
vorausgesetzt)?
b) Welches Drehmoment muss dafür an der Achse zur Verfügung stehen?
c) Wie viele Umdrehungen machen die Räder bis zum Ereichen der Geschwindigkeit
100 km/h?
Bewertung:
• Der Lösungsweg muss immer nachvollziehbar dokumentiert sein.
• Für jede Aufgabe werden maximal 10 Punkte vergeben.
• Richtige Teillösungen werden bewertet.
Punkte
5
10
15
20
25
30
35
40
45
50+
Note
1-2
2
2-3
3
3-4
4
4-5
5
5-6
6
11.05.2011/SB
Seite 3/3
Vordiplomprüfung 2011: Lösungen
ORIGIN
1
Aufgabe 1a
42
42
37
F
. newton
34
α
15
i
148
35
. deg
261
1 .. last( F )
F rx
Fi. cos αi
F rx = 25.339 newton
Fi. sin αi
F ry = 13.394 newton
i
F ry
i
Fr
F rx
2
F ry
αr
atan
M
F rx. 1. m
2
F ry
F rx
F r = 28.661 newton
if F rx < 0 . newton , π , 0
α r = 27.86 deg
F ry. 2 . m
M = 1.448 newton. m
Aufgabe 1b
FG
30. kg. g
FA
5000. newton
Momentensatz (Hebelgesetz):
F A. 1 . m F G. 0.5. m
F. 2 . m
F
F A. 1 . m
F G. 0.5. m
2. m
F = 2426.45 newton
F
g
= 247.429 kg
Aufgabe 2
50. kg
M
12. deg
α
B
1. m
H
1.8. m
1.4. m
h
µ0
Kriterium für Gleichgewicht auf der schiefen Ebene: atan µ 0 = 24.228 deg
µ
0.45
0.35
atan( µ ) = 19.29 deg
Berechnung:
M. g
FG
β
atan
F G = 490.332 newton
B
β = 29.055 deg
Winkel der Diagonalen
Hyp = 1.03 m
halbe Diagonale
d = 301.953 mm
Abstand Schwerelinie-Kippkante
M S = 148.058 newton. m
Standmoment
F = 113.882 newton
Anschiebekraft
M K = 159.435 newton. m
Kippmoment
S = 0.929
Standsicherheit
H
Hyp
d
1.
2
F G. d
MS
F G. sin( α )
F
µ 0. cos( α )
F. h
MK
S
2
B H
2
Hyp. sin( β α )
MS
MK
Der Schrank kippt um.
Aufgabe 3
D
80. mm
b
30. mm
b
c
3
10. mm
r
2 . c. 1.5. c
c
A
2.
D
2
2
2.
r π
600
A=
100
2
mm
c
2. c
D
x
157.08
D
4
c
90
3
x = 96.667
4. r
mm
84.244
3. π
2
3
V
2. π. A. x
V = 195.409 cm
ρ
gm
1.2.
3
cm
V. ρ = 234.491 gm
A = 342.92 mm
Volumen
Gewicht
3
A. x = 31100.296 mm
A. x
A
= 90.692 mm
Aufgabe 4
48. deg
α
161. deg
β
m1
100. kg
m2
350. kg
µ 10
0.32
µ 20
0.36
µ1
µ2
0.19
0.21
Resultierende Hangkräfte nach unten
m 1 . g. sin( α )
F1
γ
α
(π
µ 10. cos( α )
β)
m 2 . g. sin( γ )
F2
µ 20. cos( γ )
F 1 = 518.794 newton
Kraft links
γ = 29 deg
Neigung auf Seite 2
F 2 = 583.312 newton
Kraft rechts
F1 und F2 wirken in die gleiche Richtung. Die Reibung bei 1 ist kleiner als bei 2 und das Gefälle
grösser, m2 kann also m1 nicht einholen.
Fr
m 1 . g. sin( α )
µ 1. cos( α )
m 2 . g. sin( γ )
µ 2. cos( γ )
resultierende Kraft während der
Bewegung
F r = 1637.709 newton
Fr
a
m1
s
a = 3.639
m2
m
sec
1. . .
2
a ( 3 sec )
2
Beschleunigung
2
m1 ist soviel weiter unten
s = 16.377 m
Aufgabe 5
µ
0.06
m tot
a)
Fw
b)
v
75. kg
m tot. g. ( sin( α )
α
µ. cos( α ) )
km
25.
hr
v = 6.944
atan( 2 . % )
α = 1.146 deg
Fw = 66.672 newton
m
sec
m
2.
2
sec
g. µ
a Brems
10. kg
2
v
s Brems
s Brems = 9.316 m
2 . a Brems
Aufgabe 6
m Auto
d Rad
a)
1320. kg
2.7. m
0.9. m
dS
FG
0.51
m Auto. g
F G. d S
F h = 4314.926 newton
dA
F h. µ 0
a max
m Auto
F h. µ 0.
d Rad
a max = 1.667
Weg
Achslast hinten
m
sec
2
= 693.193 newton. m
2
2
c)
µ0
0.63. m
Fh
b)
dA
v
2. a
max
Weg = 231.417 m
Weg
= 116.924
d Rad. π
v
100.
km
hr