Gesamtes Skript

Die ideale Gasgleichung
Volumenausdehnung von Gasen:
• Bei konstantem Druck ist für Gase näherungsweise
V (TC ) = V (0◦C) · (1 + γTC )
⇒ V (TC ) = V (
0◦C
|{z}
=T (0) =273.15 K
)
mit
γ ≈ 1/273.15 K
273.15 K + TC
T
= V (T ) (0)
273.15 K
T
V (T )
V (T (0) )
=
= const.
T
T (0)
• Bei konstantem Volumen (Gay-Lussac-Gesetz):
p(T )
p(T (0) )
=
= const.
(0)
T
T
Ideale Gasgleichung:
• pV = const.|T , p/T = const.|V , V /T = const.|p ⇒
pV
p(0) V (0)
=
= const.
T
T (0)
• Normalbedingungen:
p(0) = 1.01325 × 105 Pa; T (0) = 0◦C = 273.15 K
V (0) = nVmol mit Vmol = 22.414 l = Molvolumen
n = Stoffmenge = N/NA
• Ideale Gasgleichung:
p·V =n·R·T =N ·k·T
R = universelle Gaskonstante = 8.3145 J K−1 mol−1
k = Boltzmannkonstante = 1.3807 × 10−23 J K−1
4 Grundlagen der Wärmelehre
22. April 2009
Kinetische Gastheorie: Druck
Einfachstes Modell eines Gases: Atome/Moleküle sind
Massepunkte, die elastisch mit Wänden und
untereinander stoßen.
Druck auf Gefäßwand:
• Kraft wird durch
Impulsübertrag
auf Wand erzeugt:
Fx =
Volumen V
mit N Teilchen
der Masse m
∆px
∆t
• In Zeit ∆t
erreichen alle Teilchen
die Fläche A, die
z
sich im Teilvolumen
y
∆V = vx ∆t · A
x
befinden und in
(+x)-Richung fliegen.
∆px =
N vx ∆tA
V
| {z
}
·
Zahl der
Teilchen
in ∆V
A
∆x = vx ∆t
1
2
|{z}
jedes zweite
Teilchen fliegt
nach rechts
·
2mv
| {z x}
Impulsübertrag
pro Teilchen
~|
N
|F
∆px
N
⇒p=
=
=
· mvx2 →
· mhvx2 i
A
A∆t
V
V
• Geschwindigkeitsverteilung ist isotrop mit Mittelwert
hv 2 i = hvx2i + hvy2 i + hvz2i ⇒ hvx2i = hv 2 i/3
2
mhv 2 i
= N hEkini
⇒p·V =N ·
3
3
4 Grundlagen der Wärmelehre
22. April 2009
Temperatur, kinetische Energie
und Freiheitsgrade
Kinetische Energie und Temperatur:
Vergleich von idealer Gasgleichung und Vorhersage
der kinetischen Gastheorie:

p·V = N ·kT

2hEkini

p·V =N ·
3
⇒
hEkini =
3
kT
2
Die Temperatur ist ein Maß für die kinetische
Energie der Atome/Moleküle !
Freiheitsgrade:
• Bewegung der Atome/Moleküle in drei Richtungen,
jede trägt im Mittel gleich viel zu hEkini bei:
1
mhvx2 i = hEkin,xi
2
1
= mhvy2 i = hEkin,yi
2
1
1
= mhvz2 i = hEkin,zi = k T
2
2
• Unabhängige Bewegungsmoden heißen Freiheitsgrade
• Freiheitsgrade von Atomen/Molekülen:
Bewegung
Translation
Rotation
Schwingung
Freiheitsgrade (FG)
ein FG je unabh. Bewegungsrichtung
ein FG je orthogonaler Drehachse
zwei FG pro Eigenschwingung
(je ein FG für hEkini und für hEpot i)
4 Grundlagen der Wärmelehre
22. April 2009
Reale Gase
Modifikationen am Modell “ideales Gas”:
• Atome/Moleküle haben Eigenvolumen Va
V → V − 4N Va = V − nb
(n = Stoffmenge)
• Atome/Moleküle ziehen sich an
⇒ Oberflächenenergie
⇒ Zusätzlicher Druck (Binnendruck pBi ∝ (N/V )2 )
p → p + pBi
an2
=p+ 2
V
• Modifizierte Gasgleichung:
an2
p + 2 · (V − bn) = nRT
V
(Van-der-WaalsGleichung)
• Typische Werte der Van-der-Waals-Koeffizienten a, b:
He a = 0.003 Nm4 /mol2 b = 0.024 m3/mol
H2 a = 0.025 Nm4 /mol2 b = 0.027 m3/mol
N2 a = 0.136 Nm4 /mol2 b = 0.039 m3/mol
ideales Gas
p
reales Gas
p
T1 < T2 < T3
E
T2
T1 < T2 < T3
T3
T3
T2
B
T1
T1
V
A
S
V
• Bei kleinen Temperaturen: p(V ) hat lokales Maximum
• Kompression bei konstantem T folgt Weg SABE, dabei
tritt zwischen A und B Verflüssigung ein
4 Grundlagen der Wärmelehre
22. April 2009
Wärme und Wärmekapazität
Wärme als innere Energie:
• Gesamte kinetische Energie in Objekt mit N
Atomen/Molekülen (AM):
f
N kT
2
Diese im Objekt gespeicherte thermische Energie
heißt Wärme und wird mit Q bezeichnet ([Q] = J).
Q kann als mechanische, elektrische, . . . Energie
zu- oder abgeführt werden.
• Früher wurde [Q] = kcal (Kilokalorie) verwendet:
1 kcal ist die Energie, die 1 kg Wasser von 14.5◦C auf
15.5◦C erwärmt.
• Energieänderung bei Temperaturänderung:
Etot =
∆Q ∝ M · ∆T
(M ∝ N )
Wärmekapazität:
Von einem Objekt pro Kelvin gespeicherte Wärme
• als Materialkonstante:
∆Q
[c] = Jkg−1 K−1
M ∆T
∆Q
molare Wärme = Cm =
= Mm c
n ∆T
[Cm ] = J mol−1 K−1
spezifische Wärme = c =
• abhängig vom speziellen Objekt:
∆Q
= cM = Cm n
∆T
[C] = J K−1
Wärmekapazität = C =
4 Grundlagen der Wärmelehre
22. April 2009
Mechanisches Wärmeäquivalent
Umwandlung mechanischer Energie in Wärme:
111
000
0
1
000
111
0
1
000
111
0
1
000
111
0
1
000
111
0
1
000
111
0
1
000
111
0
1
000
111
0
1
000
111
0
1
FF
Cu
FR
11111111
00000000
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
H 2O
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
00000000
11111111
Temperatur T
2r
k Umdrehungen
m
F=mg
• Beim Drehen des wassergefüllten Cu-Zylinders
wird mechanische Arbeit (Reibung!) verrichtet:
~R |
W = k 2πr ·|F
| {z }
=s
• Anordnung ist so eingerichtet, dass Feder beim
~F = 0) ⇒ |F
~R| = mg
Drehen entlastet ist (F
• W wird in Wärme umgewandelt:



W = k 2π r mg =  M
| Cu{z· cCu} +MH2O · cH2 O ∆T
vernachlässigbar
⇒ Messung der spezifischen Wärme von Wasser
• Literaturwert: cH2 O = 4.186 kJ/(kg K)
⇒ 1 kcal = 4.186 kJ
4 Grundlagen der Wärmelehre
22. April 2009
Der 1. Hauptsatz
Energieerhaltung:
• Bei einer Zustandsänderung tauscht das betrachtete
System Energie (∆W , ∆Q) mit seiner Umgebung aus
(oft ein “Wärmereservoir” bei konstantem T ).
• Für die Energiebilanz gilt:
∆U = ∆Q + ∆W
(1. Hauptsatz der Thermodynamik)
• Für Gase ist ∆U = ∆Q − p∆V .
• Achtung: In vielen Fällen betrachtet man
differentielle Änderungen (∆ → d).
Perpetuum mobile 1. Art:
• Eine Maschine, die mehr Energie in Form von Arbeit
abgibt, als sie in Form von Wärme aufnimmt, heißt
Perpetuum mobile 1. Art.
• 1. Hauptsatz: Es gibt kein Perpetuum mobile 1. Art
denn sonst wäre −∆W = |∆W | > ∆Q − ∆U .
Zustandsänderungen und 1. Hauptsatz:
• Isochor: ∆V = 0 ⇒ ∆U = ∆Q.
• Isobar: Wegen ∆(pV ) = V ∆p + p∆V ist
∆U = ∆Q − ∆(pV ) ⇒ ∆Q = ∆( U
{zpV} )
| +
=H=Enthalpie
• Isotherm: ∆T = 0 ⇒ ∆U = 0 ⇒ ∆Q = p∆V
Arbeit bei isothermen Prozessen:
∆W = −
ZV2
pdV = −
V1
4 Hauptsätze der Wärmelehre
ZV2
V1
V2
nRT
pdV = −nRT ln
V
V1
29. April 2009
2. Hauptsatz,
reversible und irreversible Prozesse
2. Hauptsatz:
Anschauliche Formulierung:
Wärme fließt von selbst immer nur
vom warmen zum kalten Objekt, nie umgekehrt.
Reversible und irreversible Prozesse:
• Prozesse mit Wärmetransport warm→kalt:
∆Q : T1 → T2 < T1
sind irreversibel, d.h. ohne Energiezufuhr von außen
unumkehrbar.
T2 >Tf >T1 oder
T1 >Tf >T2
Beispiel
geht
T1 ,V
T ,V
f
T2
Tf
geht nicht
Wegen
Reibung etc.
sind alle
realen Prozesse
irreversibel
• Reversible Prozesse sind umkehrbar, d.h. sie können
in beide Richtungen ablaufen. Die Abfolge
Beispiel
(p1, V1, T1 ) → (p2, V2, T2 ) → (p1 , V1, T1 )
ist ohne Energiezufuhr von außen möglich, ohne dass
sich Anfangs- und Endzustand von System und
Wärmereservoir unterscheiden.
Nur für
∆T = 0
p 1 ,V1 ,T
p ,V ,T
(isotherm)
geht beides
2 2
oder ∆Q = 0
T
T
(adiabatisch)
4 Hauptsätze der Wärmelehre
29. April 2009
Der 3. Hauptsatz
Mikroskopische Deutung der Entropie:
• Statistische Mechanik und Quantenmechanik
ergeben mikroskopische Definition der Entropie
(definiert auch die additive Konstante):
S = k ln W
k = Boltzmann-Konstante = 1.387 × 10−23 J/K
W = Wahrscheinlichkeitsmaß
• Das Wahrscheinlichkeitsmaß W ist die Zahl der
(quantenmechanischen) Realisierungsmöglichkeiten
eines gegebenen Zustandes.
23
Achtung: riesige Zahlen, typisch 10NA ∼ 1010 .
Der 3. Hauptsatz
• Bei Temperatur T = 0 sind alle Atome/Moleküle im
Grundzustand, d.h. sie haben keine kinetische oder
sonstige Energie
• Generell gilt:
⇒ W=1 ⇒ S=0
S(T =0) = 0
Nernst’sches Theorem,
3. Hauptsatz
• Daraus folgt (ohne Beweis):
Es ist prinzipiell
unmöglich, den absoluten
Temperatur-Nullpunkt zu
erreichen.
4 Hauptsätze der Wärmelehre
29. April 2009
Wärmekapazität von Gasen
(V = const.)
Arbeit und Volumenänderungen:
• Beispiel: Kompression
eines Gases im Kolben.
Dazu ist Arbeit
A
∆W = F · ∆s = p · A · ∆s
= p · ∆V
F
11111111111111
00000000000000
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
p, V
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
00000000000000
11111111111111
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
nötig.
• Dieses Ergebnis gilt
unabhängig von der
∆s
Form des Volumens.
• Achtung: i.a. ist p = p(V ) und damit
∆W =
ZV2
p(V )dV
V1
Wärmekapazität cV :
• Bei V = const. wird Energieänderung vollständig in
Temperaturänderung umgesetzt (da ∆W = 0):
∆Q =
f
fk
N k∆T ⇒ cV =
;
2
2m
He f = 3 (Translation)
bei allen T
N2 f = 3 (Translation)
bei niedrigen T
f = 5 (Transl.+Rot.)
bei mittleren T
f = 7 (T+R+Schw.)
bei hohen T
4 Grundlagen der Wärmelehre
CmV =
f
R
2
CmV /R
N2
3.5
2.5
1.5
He
200K
600K
T
29. April 2009
Wärmekapazität von Gasen
(p = const.)
Wärmezufuhr bei konstantem Druck
Wird einem Gas bei konstantem p Wärme ∆Q
zugeführt, so dehnt es sich unter Temperaturzunahme
R
aus und verrichtet dabei mechanische Arbeit p(V )dV .
Energieerhaltung:
∆Q = CmV n∆T +
p ·∆V
|{z}
=const.
Berechnung von p∆V mit der idealen Gasgleichung:
pV = nRT
p(V + ∆V ) = nR(T + ∆T )
p∆V = nR∆T
(i)
(ii)
(ii)–(i)
Damit wird
∆Q = CmV n∆T + nR∆T = (CmV + R) (n∆T )
{z
}
|
=Cmp
⇒ Cmp = CmV + R =
f +2
f
R+R =
R
2
2
Adiabatenkoeffizient
Definition:
κ=
Cmp
f +2
2
=
=1+ >1
CmV
f
f
κ heißt Adiabatenkoeffizient.
4 Hauptsätze der Wärmelehre
29. April 2009
Adiabaten
Zustandsänderungen mit ∆Q = 0:
• Ohne Austausch von Wärme kann nur innere
Energie U in mechanische Arbeit umgewandelt
werden (oder umgekehrt).
• Solche Zustandsänderungen heißen adiabatisch.
• Anwendung des 1. Hauptsatzes:
∆U = ∆W
nRT
⇒ nCmV ∆T = −
∆V
V
ZT2
ZV2
dT
R
dV
⇒
=−
T
C{z
V
mV}
|
T1
V1
=κ−1
⇒
ln
T2
T1
= − ln
V2
V1
κ−1
⇒
T2 V2κ−1
T1 V1κ−1
!
=1
• Daraus (mit T = pV /nR) folgen die
Adiabaten- bzw. Poisson’schen Gleichungen:
T · V κ−1 = const.
p
bzw.
p · V κ = const.
Adiabaten
(p~1/Vκ )
Isothermen
(p~1/V)
T3
Wichtig z.B.
bei chemischen
Reaktionen
T2
T1
V
4 Hauptsätze der Wärmelehre
29. April 2009
Konvektion
Prinzip:
• Fluides Medium
dehnt sich durch
Erwärmung lokal aus
→ erwärmte
Stoffmenge hat
kleinere Dichte
→ steigt auf und
wird durch kälteren
Stoff ersetzt
→ Konvektionskreislauf
Warme Flüssigkeit
steigt auf
Zone lokaler
Erwärmung
Kalte Flüssigkeit
sinkt ab
• Bei Konvektion ist Wärmetransport an Materialtransport gebunden!
Beispiel: See- und Landwind
• Konvektion ist extrem wichtig für Wetterablauf,
Klima, Ozeane etc.
• Beispiel: Windbildung an Küsten im warmen Klima
(z.B. Mittelmeer)
Tag
warme Luft
steigt auf
Nacht
kalte Luft
strömt nach
m
kalt
war
kühl
Seewind
4 Wärmetransport
kühl
Landwind
06. Mai 2009
Wärmeleitung
Prinzip:
• Wird starres Medium
lokal erwärmt, breitet T2
sich die Wärme durch
Stöße der AM bzw.
Elektronen aus.
• Dabei erfolgt kein
T1
Materialtransport.
• Die Wärmeleitung ist
Geometrie- und
materialabhängig:
dT
dQ
= −λA
dt
dx
• λ = Wärmeleitzahl:
Material
Kupfer
Eisen
Beton
Glas
Wasser
Luft
λ [ W/(mK)]
393
67
2.1
0.8
0.6
0.026
T
stationärer
Zustand
Aufwärmvorgang
x
dx
T1
T2 >T1
T
T+dT
Stab mit
konstantem
Querschnitt A
dQ/dt
Kommentar
Metalle: Wärmeleitung
durch Leitungselektronen
Stöße der AM im
Festkörper
Stöße der AM in Flüssigkeit
Klein wegen geringer Dichte
Wärmeleitungsgleichung:
• Raum- und Zeitabhängigkeit der Temperatur im
allgemeinen (nicht-stationären) Fall:
λ ∂ 2T
∂ 2T
∂ 2T
∂T
=
+
+
∂t
cρ ∂x2
∂y 2
∂z 2
• Wichtig z.B. bei Berechnung der Wärmeverluste
durch Wände oder Fenster!
4 Wärmetransport
06. Mai 2009
Wärmestrahlung
Prinzip:
• Wärme (d.h. die kinetische Energie der AM) wird
in elektromagnetische Strahlung umgesetzt, die von
jedem Körper abgestrahlt (und absorbiert) wird.
• Die Wellenlänge der Strahlung fällt mit T :
Mensch, Herdplatte: infrarot
Glühende Kohle, Sonne: sichtbar
• Wärmetransport durch Strahlung ist nicht an
Vorhandensein von Materie gebunden
⇒ sonst würde keine Energie von der Sonne
zu uns kommen!
Das Stefan-Boltzmann’sche Gesetz:
• Die gesamte als Wärmestrahlung abgegebene
Leistung einer Fläche A mit Temperatur T ist
dQ
= −ǫσAT 4
dt
W
=
K 4 m2
Stefan-Boltzmann-Konstante
ǫ = Emissionsgrad, 0 ≤ ǫ ≤ 1
σ = 5.77 × 10−8
• ǫ hängt ab von Material, Oberflächenbeschaffenheit,
Farbe: umso heller/spiegelnder, desto kleiner ist ǫ.
Versuch:
Wärme−
Strahlung
4 Wärmetransport
Detektor
Messung der
Strahlungsleistung
verschiedener
Seiten eines
geheizten Würfels.
06. Mai 2009
Die elektrische Ladung
Elektrische Ladung ist die Quelle aller
elektrischen Phänomene
Eigenschaften der elektrischen Ladung:
• Es gibt positive und negative Ladungen.
• Gleichnamige Ladungen stoßen sich ab,
ungleichnamige ziehen sich an:
F12
+
F12
F21
+
+
−
−
F21
−
F12
F21
• Physikalisches Symbol und Einheit:
Ladung = Q ;
[Q] = C = Coulomb
• Ladung ist in ganzzahligen Vielfachen einer
Elementarladung e gequantelt:
e = +1.602 × 10−19 C .
• Ladung ist stets an Teilchen gebunden:
Teilchen
Ladung
Elektron
Qe = −e = −1.602 × 10−19 C
Proton
Qp = +e = +1.602 × 10−19 C
Qn = 0
Neutron
Atomkern QKern = +Ze
• In einem abgeschlossenen System ist die
Gesamtladung erhalten:
X
Qtot =
Qi = const.
i
Durch Ladungstrennung können auch bei Qtot = 0
elektrische Phänomene erzeugt werden.
5 Grundlagen der Elektrizitätslehre
06. Mai 2009
Ladungstrennung und -messung
+
+
Ladungstrennung:
+
+
• Reiben verschiedener
Materialien (Isolatoren)
aneinander
→ Elektronen wandern
bevorzugt zu einem
Material
→ Ladungstrennung.
• Bandgenerator:
kontinuierliche
Aufladung durch
Ladungstrennung.
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
Ladungs−
abgriff
+
+
Band
(z.B. Gummi)
+
Metall−
Hohlkugel
−
−
−
−
−
−
Ladungs−
trennung
−
−
−
− −
Ladungsmessung:
• Ausnutzung der
Abstoßung
gleichnamiger
Ladungen.
isolierender
Rahmen
• Zum Beispiel in
Elektrometer:
Drehmoment auf
Zeiger steigt
mit Gesamtladung.
5 Grundlagen der Elektrizitätslehre
Ladung Q
Metall
Q
06. Mai 2009
Ladungstransport und Strom
Ladungstransport:
• Ladung immer an (massebehaftete) Teilchen
gebunden
⇒ Ladungstransport ist immer mit
Materialtransport verbunden.
• Verschiedene Transportmechanismen:
– Elektronen in elektrischem Leiter (z.B. Metall);
– Ionen in Flüssigkeit (z.B. Salzlösung);
– Funken: Stromfluss entlag einem “Kanal”
ionisierten Gases;
– “Ladungslöffeln”: Transport eines
makroskopischen geladenen Objekts.
Elektrischer Strom:
Ladungstransport pro Zeit durch eine gegebene
Querschnittsfläche (z.B. Drahtquerschnitt)
• Definition:
dQ
∆Q
=
= Q̇
∆t→0 ∆t
dt
C
[I] = Ampère = A =
s
el. Strom = I = lim
• Ampère ist eine SI-Basiseinheit
– Ladungseinheit Coulomb ist davon abgeleitet.
– Definition von Ampère über Kraftwirkung
stromdurchflossener Drähte aufeinander
(siehe Kap. 4.3).
5 Grundlagen der Elektrizitätslehre
06. Mai 2009
Das Coulomb-Gesetz
Kraft zwischen zwei Punktladungen:
1
r
Q1Q2 ~
(Coulomb-Gesetz)
·
·
4πǫ0
r2
|~
r|
ǫ0 = Dielektrizitätskonstante
~C =
F
= 8.854 × 10−12 A2 s4 kg−1 m−3
FC (Q1 Q2 <0)
Q1
FC (Q1 Q2 >0)
r
Q2
• Richtungskonvention:
~C ist die Kraft auf die Ladung, zu der ~
F
r zeigt.
• 3. Newton’sches Axiom:
Die Ladungen üben entgegengesetzt gleiche Kräfte
aufeinander aus.
Vergleich mit Gravitationsgesetz:
~C
Coulomb: F
Ladungen Q1Q2
1/4πǫ0
∝ 1/r2
anziehend oder abstoßend
~C |
|F
=
~G|
|F
~G
Gravitation: F
Massen m1 m2
G
∝ 1/r2
immer anziehend
1
|4πǫ
{z0 G}
·
Q1Q2
m1m2
=1.347×1020 C2 /kg2
Z.B. Elektron und Proton (Wasserstoffatom):
~C |
|F
=
~G|
|F
1.347×1020 C2 /kg2 · (1.6×10−19 C)2
−31
{z
|9.1×10
=me
kg · 1.67×10−27 kg
} |
{z
=mp
5 Grundlagen der Elektrizitätslehre
}
= 0.22 × 1040
13. Mai 2009
Das elektrische Feld
Definition:
Eine Anordnung von Ladungen erzeugt am Ort ~
r
~
die Coulomb-Kraft FC auf eine Probeladung q:
~C (~
F
r)
~
E(~
r ) = elektrisches Feld =
q
N
kg m
[E] =
=
C
A s3
Feld einer Punktladung:
~ erzeugt bei ~
Eine Punktladung Q am Ort R
r das Feld
~
Q
~
r−R
~
E(~
r) =
·
~ 3
4πǫ0 |~
r − R|
Feld mehrerer Ladungen:
~i
• Bei mehreren Punktladungen Qi an den Orten R
addieren sich die Coulomb-Kräfte vektoriell:
~ r) =
E(~
~i
X Qi
~
r−R
·
~ i |3
4πǫ
r−R
0 |~
i
• Allgemeiner Fall: Ladungsdichte-Verteilung ρ(~
r)
→ Ladung dQ in Volumen dx dy dz am Ort ~
r:
dQ = ρ(~
r ) · dx dy dz
R 3
→ Gesamtladung: Qtot = V d r ρ(~
r).
→ Elektrisches Feld:
Z
~
~) ~
r−R
ρ(R
3
~
·
E(~
r) = d R
~ 3
4πǫ0 |~
r − R|
V
5 Grundlagen der Elektrizitätslehre
13. Mai 2009
Feldlinien
Eigenschaften:
• Feldlinien sind an jedem
Punkt parallel zum
E-Feld.
+
• Feldlinien zeigen von
positiven zu
negativen Ladungen.
r
E( r )
• Feldlinien beginnen und
enden ausschließlich
am Ort von Ladungen.
(Achtung:
bildliche Darstellung
oft unvollständig)
−
Sichtbarmachung:
• Elektrisches Feld in
isolierender Flüssigkeit
(z.B. Speiseöl).
• Feld erzeugt
Ladungstrennung in
kleinen Körnchen
auf der Flüssigkeit
(z.B. Gries).
• Elektr. Anziehung
in Feldlinienrichtung.
• Körnchen orientieren
sich entlang der
Feldlinien.
+ +
+ +
++
+
++ +
+ ++
+
− −
−−
− −−
+ + ++
++ +
E
−−
− −−
− −
Grieskörner
Coulomb−
Anziehung
− −− −
−−−
5 Grundlagen der Elektrizitätslehre
13. Mai 2009
Potential und Spannung
Arbeit bei Ladungsverschiebung:
• Beim Verschieben einer Ladung q im elektrischen Feld
~ r ) entlang dem Weg C wird Arbeit geleistet:
E(~
Z
Z
~ d~s
~C d~s = q E
Wel = F
C
• Vorzeichen: Wel > 0
wenn die Arbeit vom
~ geleistet wird.
Feld E
• E-Feld ist konservativ R
1
⇒ Wel hängt nur von
den Endpukten des
Weges C ab, aber
aber nicht vom Verlauf.
C
R2
C
(0,0,0)
Elektrostatisches Potential:
• Arbeit, um eine Probeladung q vom Punkt ~
r
in unendliche Entfernung von der Feldquelle zu
bringen:
q
Z∞
~ d~s = q · Φ(~
E
r ) = q · (elektrostatisches Potential)
~
r
kg m2
• Einheit: [Φ] = J/C =
= Volt = V .
A s3
• Φ hängt nur von ~
r ab; Konvention: Φ(∞) = 0.
• Spannung:
Z
~ d~s = Φ(R
~ 1 ) − Φ(R
~ 2 ) = Spannung U
E
C
[U ] = Volt
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Potential einer Punktquelle
Berechnung:
• Elektrisches Feld einer Punktladung Q im Ursprung
zeigt radial nach außen.
~ d~s = E dr und damit
• E
Z∞
dr′
Q
Φ(~
r ) = Φ(r) =
4πǫ0
r ′2
∞ r
Q
Q
1
=
=
− ′
4πǫ0
r r
4πǫ0 · r
z
ds
Φ (r)
r
Q>0
Q
y
x
U
R1
R2
r
Q<0
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Beschleunigung im
elektrischen Feld
Potential und Energie:
• Beim Durchlaufen der Spannung U ändert sich die
potentielle Energie eines Teilchens mit Ladung q um
∆Epot = −q · U
• Wegen Energieerhaltung:
∆Ekin = −∆Epot = q · U
• Geladene Teilchen nehmen aus einem elektrischen
Feld kinetische Energie auf, wenn sie es in der
“richtigen” Richtung durchlaufen.
• Beispiele:
– Elektronenstrahl im Fernseher
– Teilchenbeschleuniger
Elektronenvolt:
• Spezielle Energieeinheit für mikroskopische Objekte
(Atome, Kerne, Teilchen):
1 eV = 1 Elektronenvolt = e · 1 V = 1.602 × 10−19 J
• Oft verwendete Vielfache:
1 keV = 103 eV
(Kiloelektronenvolt)
1 MeV = 106 eV
(Megelektronenvolt)
1 GeV = 109 eV
(Gigaelektronenvolt)
• Typische Energieskalen:
– Bindungsenergien in Atomen und Molekülen: eV;
– Röntgenstrahlen: keV;
– Atomkerne: MeV;
– Elementarteilchen: GeV.
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Feld und Potential;
Elektrische Leistung
Feld und Potential:
• Das elektrische Feld kann mit Hilfe der
Definitionsgleichung des elektrostatischen Potentials
aus Φ(~
r ) berechnet werden:
∂Φ
∂Φ
∂Φ
~ r ) = −gradΦ(~
,
,
E(~
r) =
∂x ∂y ∂z
~ r ) zeigt entgegen der Richtung
• Das Feld E(~
r ).
der stärksten Zunahme von Φ(~
~ r ) steht sekrecht auf Flächen mit
• Das Feld E(~
Φ(~
r ) = const. (Äquipotentialflächen).
Elektrische Leistung:
• Elektrische Arbeit beim Transport der Ladung ∆Q
über Spannung U :
∆Wel = ∆Q · U
• Wenn dies in einer Zeit ∆t geschieht (U = const.)
∆Wel
∆Q
= lim
·U =I ·U
∆t→0 ∆t
∆t→0 ∆t
Pel = lim
• Beispiel:
Batterie mit U = 1.5 V und Gesamtladung 1 Ah liefert
Gesamtenergie
Wel = ∆t · I · U = 3600 s · 1 A · 1.5 V = 5.4 kJ
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Das Ohmsche Gesetz
Strom und Spannung:
• Legt man eine Spannung U an ein Material an, so
fließt im allgemeinen ein Strom I.
• Veranschaulichung im Schaltbild:
Material
(el. Widerstand)
I
Spannungsquelle
+
−
U0
• Für viele Materialien (Metalle, homogene Halbleiter)
gilt bei konstanter Temperatur:
I∝U
⇒
U
= el. Widerstand = const.
I
[R] = V/ A = Ω = Ohm
R=
(Ohm’sches Gesetz)
Strom-Spannungs-Kennlinien:
U
Beispiele
nichtlinearer
Fälle:
U
nicht−linear
Gasentladung
Diode
Glühlampe
linear
(Ohmsch)
I
5 Grundlagen der Elektrizitätslehre
I
20. Mai 2009
Spezifischer Widerstand
Definition:
Der Widerstand eines Drahtes mit Länge L und
Querschnittsfläche A ist
L
1 L
R = ρs · = ·
A
σ A
ρs = spezifischer el. Widerstand
[ρs] = Ωm
σ = spezifische el. Leitfähigkeit
[σ] = Ω−1m−1
L
A
Typische Werte (bei 20◦C):
Material
Kupfer Cu
Eisen Fe
Graphit
Teflon
Hartgummi
spezifischer Widerstand [10−6 Ωm]
0.017
∼ 0.1
∼ 8
1021
1019 . . . 1022
• Der spezifische Widerstand hängt vom Material
(Leitungsmechanismus, mikroskopische Struktur)
und von der Temperatur ab.
• Variiert über fast 30 Größenordnungen!
• Der Wert von ρs in 10−6 Ωm entspricht
dem Widerstand in Ω eines Drahtes mit
Länge L = 1 m und Querschnitt A = 1 mm2.
• Für Metalle (Leitung durch Elektronentransport) sind
elektrische und Wärmeleitfähigkeit proportional.
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
T -Abhängigkeit des Widerstandes
Metalle:
ρs
• Widerstand durch
Stöße der Elektronen
mit Gitteratomen.
• Steigt mit zunehmender
Bewegung der Atome.
• Widerstand nimmt
mit steigender
Temperatur zu.
Halbleiter:
Metall
T
ρs
• Leitung durch Elektronen,
die durch thermische
Energie aus lokaler
Bindung gelöst werden.
• Mit steigendem T nimmt
Zahl der Ladungsträger zu
und Widerstand ab.
• Bei hohen T Widerstandszunahme wie in Metall.
Supraleiter:
• Bei einigen Materialien
wird ρs = 0 bei T < Tc
(Tc : kritische Temperatur,
Sprungtemperatur).
• Quantenmechanischer
Effekt.
• Typisch: Tc (Hg) = 4.183 K;
HochtemperaturSupraleiter: Tc & 100 K .
5 Grundlagen der Elektrizitätslehre
Halbleiter
TRaum
T
ρs
Supraleiter
Tc=einige K
(bei einigen
Stoffen bis
mehrere 10K)
Tc
T
20. Mai 2009
Kirchhoffsche Regeln
Knotenregel:
• Knoten = Kontaktstelle
mehrerer Drähte
ohne aktives Element
• Gesamtladung im Knoten
ist erhalten
⇒
n
X
I1
I2
Ii = 0
I3
i=1
• Vorzeichen geben
Richtung der Ströme!
• Knotenregel bzw.
1. Kirchhoffsche Regel
I4
Knoten
U1
Maschenregel:
• Masche = Leitungskreis
mit Spannungsquelle(n)
und Widerstände(n).
~ s
• Wegintegral von Ed~
entlang Masche verschwindet
n
X
i=0
Ui = I
n
X
i=1
R1
U0 +
−
I
I
Ri − |U0| = 0
• Spannungen von Quelle
und an Widerständen
haben entgegengesetzte
Vorzeichen.
• Maschenregel bzw.
2. Kirchhoffsche Regel
5 Grundlagen der Elektrizitätslehre
R2
U2
20. Mai 2009
Hintereinander- und
Parallelschaltung von Widerständen
Hintereinanderschaltung:
• Mehrere Widerstände Ri (i = 1, . . . n) in einer Masche
mit Spannungsquelle U0
• Maschenregel:
X
|U0| = I ·
Ri
• Gesamtwiderstand ist
Rtot =
|i=1
{z }
=Rtot
n
X
Ri
i=1
Parallelschaltung:
• Knotenregel:
I0 = I1 + I2
I1 I2
I0
• Maschenregel:
U0 = I1 R1 = I2 R2
• Gesamtwiderstand:
+ U
− 0
R1
R2
1
1
I0
1
=
+
=
Rtot
U0
R1
R2
• Allgemeiner Fall:
n
X 1
1
=
Rtot
R
i=1 i
5 Grundlagen der Elektrizitätslehre
27. Mai 2009
Influenz
Leiter im äußeren elektrischen Feld:
~
• E-Feld
verursacht Kraft auf frei bewegliche
Ladungsträger im Leiter.
• Ladungsträger arrangieren sich so, dass insgeseamt
keine Kraft auf sie wirkt
⇒ resultierende Ladungsverteilung erzeugt ein Feld
~ infl , das das äußere Feld E
~ gerade kompensiert.
E
• Dieser Vorgang heißt Influenz, die dabei erzeugten
Ladungsverteilungen Influenzladungen.
äußeres Feld
negative
Influenzladungen
an Oberfläche
influenziertes
Gegenfeld
E
+ +
− −
−
++
−−
−
++
E infl
−
−
+
−
+
−
+
−−
+
+
−−
+
+
−−
−
+ +
leitender
Körper
positive
Influenzladungen
an Oberfläche
E
Konsequenzen:
• Im Inneren von Leitern ist das statische elektrische
~ = 0.
Feld stets E
• Die Influenzladungen sammeln sich an den
Oberflächen des Leiters.
~ senkrecht zur
• An der Oberfläche des Leiters steht E
Oberfläche (sonst gäbe es eine resultierende Kraft
parallel zur Oberfläche auf die Ladungsträger).
5 Statische elektrische Felder
27. Mai 2009
Der Plattenkondensator
Prinzip:
• Zwei planparallele Leiterplatten im Abstand d und mit
Fläche A werden an eine Spannung U angeschlossen.
• An der Innenseite der Platten bilden sich entgegengesetzt gleiche Flächenladungsdichten σ± = Q±/A aus,
die bis auf Randeffekte homogen sind.
Flächenladungsdichte
σ+
+
+
+
+
+
+
+
+
+
+
d
−
−
−
−
−
−
−
−
−
−
Flächenladungsdichte
σ−
Fläche A
x
+
−
U
Feld, Spannung, Ladung:
• Elektrisches Feld:
~ = const. nach Aufladevorgang.
– U = const. ⇒ E
– Im Inneren des Kondensators (σ = |σ±|):
~ = E+ x̂ + E− x̂ = (σ/ǫ0)x̂
E
~ = 0.
– Außen: E
• Spannung und Ladung:
U = Ed =
Qd
σ
d=
ǫ0
ǫ0 A
(Q = |Q±| ist “die Ladung auf dem Kondensator”.)
5 Statische elektrische Felder
27. Mai 2009
Die Kapazität
Aufladbare Systeme und Kapazität:
• Für Systeme, die bei Anlegen einer Spannung U eine
Ladung Q speichern können, gilt stets
Q∝U
⇒
C = Kapazität =
Q
U
C
A2 s4
[C] =
=
= F = Farad
V
kg m2
(Einheit benannt nach Michael Faraday, 1791–1867).
• Beispiele:
Plattenkondensator:
Metallkugel, Radius r:
ǫ0 A
d
C =4πǫ0 r
C=
Zahlenbeispiel, Vielfache von Farad:
• Kapazität eines Plattenkondensators
mit d = 1 mm und A = 100 cm2 :
2 4
ǫ0 A
−12 A s
C=
= 8.854 × 10
· 10 m
d
kg m3
= 8.854 × 10−11 F
• Kapazitäten sind meist winzige Bruchteile von 1 F
⇒ typische Einheiten:
1 pF = 10−12 F
(Pikofarad)
1 nF = 10−9 F
(Nanofarad)
1 µF = 10−6 F
(Mikrofarad)
5 Statische elektrische Felder
03. Juni 2009
Hintereinander- und
Parallelschaltung von Kapazitäten
Hintereinanderschaltung:
• Maschenregel:
U0 = U1 + U2 + U3
• Alle Ladungen sind
gleich:
C1 , U1
+ U
0
-
Q1 = Q2 = Q3 = Q
• Gesamtkapazität
(allgemeiner Fall):
C2 , U2
ungeladen
C3 , U3
n
X 1
U0
1
=
=
Ctot
Q
C
i=1 i
Parallelschaltung:
C1 , Q1
• Maschenregel:
U0 = U1 = U2 = U3
C2 , Q2
• Gesamtladung:
Qtot = Q1 + Q2 + Q3
C3 , Q3
• Gesamtkapazität
(allgemeiner Fall):
5 Statische elektrische Felder
+
Ctot
-
n
X
Qtot
=
=
Ci
U0
i=1
U0
03. Juni 2009
Energiedichte im elektrischen Feld
Elektrische Arbeit beim
Aufladen eines Kondensators:
• Um bei Spannung U in einem Kondensator die
Ladung um ∆Q zu erhöhen, ist eine Arbeit
∆Wel = U · ∆Q = (Q/C) · ∆Q notwendig.
• Integration über Gesamtladung:
Wel =
ZQ
0
Q2
1
Q′ dQ′
=
= CU 2 .
C
2C
2
• Dieses Ergebnis gilt für jedes aufladbare System!
Energiedichte:
• Mit C = ǫ0 A/d und U = Ed
(Plattenkondensator mit Fläche A und Abstand d):
ǫ0AE 2d2
1
1
2
= ǫ0 |{z}
Ad E 2 .
Wel = CU =
2
2d
2 =V
• Energiedichte:
1
Wel
= ǫ0E 2 ;
[wel ] = J/m3 .
V
2
• wel ist die Energie pro Volumen, die zur Erzeugung
des Feldes (der felderzeugenden Ladungsverteilung)
aufzubringen ist.
• Das Ergebnis
1
wel = ǫ0 E 2
2
gilt unabhängig von
– der Gestalt des Feldes
– der Art seiner Erzeugung.
wel =
5 Statische elektrische Felder
03. Juni 2009
Isolatoren im elektrischen Feld
Experimentelle Beobachtung:
• Bringt man bei fester Ladung Q einen Isolator in das
Feld eines Plattenkondensators, so nimmt die
Spannung am Kondensator ab:
d
d
Q
leer:
Isolator:
U=U0
E=E 0
U<U0
E<E 0
U
U
• Die Kapazität nimmt zu:
C=
Q
Q
> C0 =
U
U0
• Die Feldänderung wird durch die
Dielektrizitätskonstante ǫ > 1 beschrieben:
U =U0/ǫ = E0d/ǫ
E =E0/ǫ
A
C =C0 · ǫ = ǫǫ0
d
• Im Vakuum ist ǫ = 1, in Luft ǫ ≈ 1.0005
⇒ Luft ist für elektrische Felder “fast wie Vakuum”.
5 Statische elektrische Felder
03. Juni 2009
Polarisationsladungen
Induzierte Ladungsverschiebung:
• Im Isolator gibt es keine freien Ladungsträger, aber
in jedem Atom können die positiven und negativen
Ladungen gegeneinander verschoben werden:
−
−
−
− + −
−
−
− −
−
−
−
− d +
− −−
− −
r− =r+
r+ −r− =d
E
• Durch die Kraftwirkung des elektrischen Feldes
werden die Ladungsschwerpunkte
P
(±)
Q
~
ri
~
r± = Pi i (±)
i Qi
um eine Strecke d~ in Feldrichtung getrennt.
Polarisations-:
Ladungsdichte:
• Im Isolator (“Dielektrikum”)
bilden sich geladene
Oberflächenschichten.
• Ladungsdichte:
σpol =
1
N Ad QZ = N dQZ
A |{z}
=V
N = Zahl d. Atome/Volumen
QZ = Kernladung
5 Statische elektrische Felder
negative
Polarisationsladungen
σ pol=Q pol /A
+
+
+
+
+
+
+
+
+
+
1111111111111111
0000000000000000
000000000000000
111111111111111
0000000000000000−
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
−
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000−
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000−
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
−
elektrisch
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
neutral
−
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000−
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000−
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
−
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000−
1111111111111111
0000000000000000
1111111111111111
000000000000000
111111111111111
0000000000000000
1111111111111111
d
d
positive
Polarisationsladungen
σ pol=Q pol /A
03. Juni 2009
Polarisation, Suszeptibilität und
Dielektrizitätskonstante
Polarisation:
• Die Polarisations-Flächenladungsdichte kann als
Vektor dargestellt werden:
As
~ = (N QZ d) · Ê ;
Polarisation = P
[P ] =
.
m2
• Im allgemeinen ist QZ d ∝ E:
Asm2
QZ d = αE ; α = Polarisierbarkeit; [α] =
V
Feld im Dielektrikum:
• Das Vakuum-Feld wird durch die PolarisationsLadungen reduziert:
P
σ − σpol
= EVak −
EDiel =
ǫ0
ǫ0
1
= EVak − N αEDiel = EVak − χEDiel
ǫ0
Nα
χ = el. Suszeptibilität =
; [χ] = 1
ǫ0
• Insgesamt: EDiel (1 + χ) = ǫEDiel = EVak
• Das elektrische Feld im Dielektrikum ist um
1/ǫ = 1/(1 + χ) schwächer als im Vakuum.
• Die Suszeptibilität ist direkt mit atomaren
Eigenschaften verknüpft (materialabhängig!)
Luft, Normalbedingungen
Benzol
Wasser
Quarzglas
Keramik
5 Statische elektrische Felder
ǫ = 1.000576
ǫ = 2.3
ǫ = 81
ǫ = 3.75
ǫ bis ∼ 1000
03. Juni 2009
Elektrisches Feld in Dielektrika
Elektrische Verschiebungsdichte:
~ r ) beschreibt
Die elektrische Verschiebungsdichte D(~
das elektrische Feld, das von den äußeren Ladungen
ρ(~
r ) erzeugt wird und somit “die Ladungen im
Dielektrikum verschiebt”:
~ = ǫǫ0 E
~;
el. Verschiebungsdichte = D
[D] =
As
.
m2
Elektrische Felder in Dielektrika:
• Grundregel:
~ r ) wird wie im Vakuum aus
Das elektrische Feld E(~
den freien Ladungen (d.h. ohne Berücksichtigung der
Polarisationsladungen) berechnet, aber mit der
Ersetzung
ǫ0 → ǫǫ0 .
• Beispiele:
– Coulomb-Feld:
~ r) =
E(~
Q
1
r
· 3 ·~
4πǫǫ0 r
– 1. Maxwellsche Gleichung:
~ r) =
divE(~
1
ρ(~
r)
ǫǫ0
⇒
~ r ) = ρ(~
divD(~
r).
– Energiedichte des elektrischen Feldes:
wel =
5 Statische elektrische Felder
1~ ~
1
ǫǫ0E 2 = D
·E
2
2
03. Juni 2009
Elektrische Dipole
Das elektrische Dipolmoment:
−Q
+Q
−
+
d
• Elektrischer Dipol = Anordnung zweier
ungleichnamiger Ladungen gleichen Betrages
in einem festen Abstand d
• Das elektrische Dipolmoment ist definiert als
p
~ = Q d~ ;
[p] = Asm .
Dipol im elektrischen Feld:
• Kraft im homogenen Feld:
+Q
~tot = F
~+ + F
~− = 0
F
+
• Drehmoment im hom. Feld:
~ = (~
~+ ) + (~
~−)
M
r+ × F
r− × F
h
i
~
= Q · (~
r+ − ~
r− ) × E
~ =p
~
= Q · (d~ × E)
~×E
d
F+
θ
E
r
−
F−
−Q
r−
r+
• Potentielle Energie im homogenen Feld:
~ = −pE cos θ
Epot = −~
p·E
~ = E(x)x̂):
• Kraft im inhomogenen Feld (für E
h
i
~
~
~tot = F
~+ + F
~− = Q · E(~
~ r + d/2)
~ r − d/2)
F
− E(~
d
dE(x)
dE(x)
= Q · 2 · cos θ
= p cos θ
2
dx
dx
5 Statische elektrische Felder
03. Juni 2009
Magnetische Phänomene
Bekannte magnetische Phänomene:
• Permanentmagnete;
• Das Erdmagnetfeld (Magnetkompass!);
• Elektromagnetismus (Erzeugung
magnetischer Kraftwirkungen durch Stromfluss).
Alle magnetischen Phänomene werden durch bewegte
Ladungen erzeugt!
Permanentmagnete:
• Magnete haben zwei
unterschiedliche Pole,
die nicht isolierbar sind.
N
S
• Ungleichartige Pole ziehen
sich an, gleichartige
stoßen sich ab.
N
S
• Die Pole werden nach
ihrer Ausrichtung im
Erdmagnetfeld benannt:
N = Nordpol:
zeigt nach Norden;
S = Südpol:
zeigt nach Süden.
S
N
Sichtbarmachung von Magnetfeldern:
• Durch Probemagnet (z.B. Kompassnadel), der die
Richtung der magnetischen Kraftwirkung anzeigt.
• Durch Eisenfeilspäne, die sich entlang der
Feldlinien (d.h. in Richtung der magnetischen
Kraftwirkung) anordnen.
6 Statische magnetische Felder
10. Juni 2009
Magnetische Feldlinien
Eigenschaften:
• Magnetische Feldlinien zeigen in die Richtung, in die
sich der Nordpol eines Testmagneten ausrichtet.
• Magnetische Feldlinien sind immer geschlossen
(auch in Permanentmagneten oder stromführenden
Bereichen)
⇒ es gibt keine magnetischen Ladungen.
−
S
N
I
Permanentmagnet
gerader
Draht
I
Spule
6 Statische magnetische Felder
10. Juni 2009
Das Magnetfeld
Phänomenologisch:
~ r ) mit
Das Magnetfeld ist ein Vektorfeld B(~
• Richtung, in die sich Testmagnet ausrichtet
(in Richtung des Nordpols des Testmagneten).
• Stärke proportional zum Drehmoment auf
Testmagnet.
~:
Definition von B
• Für das Magnetfeld eines geraden
stromdurchflossenen Leiters
beobachtet man experimentell:
I
r
I
B∝
r
B
• Festlegung der
Proportionalitätskonstante:
B(r) =
µ0 I
~
· = µ0H(r)
2π r
µ0 = Induktionskonstante = 4π × 10−7
[B] =
Vs
Am
Vs
= T = Tesla = 104 G[auß] (alte Einheit).
2
m
~ = Magnetfeld.
• Ältere Lehrbücher: H
• Wert von µ0 durch Wahl der Einheit A festgelegt.
• Typische Magnetfelder:
Erdmagnetfeld (Mittelwert)
Permanentmagnet (Eisen)
Supraleitende Spulen
(z.B. in Teilchenbeschleunigern)
6 Statische magnetische Felder
B = 2 × 10−5 T
B ∼ 1.5 T
bis 7 . . . 10 T
10. Juni 2009
Das Ampèresche Gesetz
Beispiel: gerader Draht
~
• Betrachte Wegintegral von B
entlang geschlossenem Weg C:
I
~ d~s
B
C
• Wähle konzentrischen Kreis um
Draht als Integrationsweg C:
⇒
I
r
C
ds B
~ k d~s, |B
~ | = B(r)
B
I
~ d~s = 2πrB(r) = 2πr µ0 · I = µ0 I
B
2π r
C
• Das B-Feld ist nicht konservativ!
Das Ampèresche Gesetz:
• Allgemein gilt:
~ entlang eines geschlossenen
Das Wegintegral von B
Weges C ist gleich µ0IA , wobei IA der Strom ist, der
durch die von C begrenzte Fläche A fließt:
I
~ d~s = µ0IA
B
(Ampèresche Gesetz)
C
~
• Das Ampèresche Gesetz bestimmt das Magnetfeld B
für eine gegebene Anordnung von Strömen eindeutig.
• Achtung: Gilt so nur für statische Felder.
6 Statische magnetische Felder
10. Juni 2009
Die Stromdichte
Ladungsträgergeschwindigkeit
und Stromdichte:
v
Ladungsträgerdichte n
.. .
. .
. .. .. .. . . .. .. ..
.
. . . . . . . . . . . . . .. .. .
. . . . . . . . .. . . . . .
. . . .. .. . . . .. . . . . .
. . . . . . . . . . . .. . . . . . .
.
.
. . . . .. . . .. .. . .. . .
. . . .
dA
v dt
• Betrachte kleines Volumen ∆V von Ladungsträgern,
die sich mit Geschwindigkeit ~v bewegen.
• Gesamtladung in ∆V (Ladung q pro Ladungsträger):
∆Q = nq · ∆V = nq · v∆t · ∆A
• Strom, der durch die Bewegung von ∆V erzeugt
wird:
∆Q
∆I =
= nqv · ∆A
∆t
• Die Stromdichte ~ ist der Strom pro durchflossener
Fläche:
A
∆I
= nq~v ; [j] =
~ =
∆A
m2
Ampèresches Gesetz mit Stromdichte:
I
~ d~s = µ0
B
C
Z
~
~ dA
A
(A ist die vom Integrationsweg C
eingeschlossene Fläche)
6 Statische magnetische Felder
10. Juni 2009
Spezielle Magnetfelder
Spule:
I
(N Windungen)
I
~ s = LB
Bd~
C
IA = N I
NI
⇒B = µ0
L
L
C
B
2R
I
2r
Weg C
R
r
Draht mit homogenem Stromfluss:
I
~ s = 2πB(r)r
Bd~

C
 r2
I 2 r≤R
IA =
R
I
r≥R
B(r) =
µ
0

I r2

2π

R


 µ0 I 1
2π r
Helmholtz-Spulenpaar:
Näherungsweise homogenes
Magnetfeld
µ0I
B=
(5/4)3/2 R
I
r≤R
r≥R
I
2R
B
R
6 Statische magnetische Felder
10. Juni 2009
Die Lorentz-Kraft
Kraft auf bewegte Ladung:
• Bewegte Ladungen z.B. in
– stromführenden Leitern;
– Teilchenstrahlen
(z.B. Fadenstrahlrohr).
• Experimenteller Befund:
~ wirkt Kraft F
~L,
Im Magnetfeld B
~ steht: q>0
die senkrecht auf ~v und B
FL
v
~L = q · (~v × B
~)
Lorentz-Kraft = F
B (in Zeichenebene
hinein)
• Achtung:
~L.
– Rechte-Hand-Regel ⇒ Richtung von F
– Vorzeichen der Teilchenladung q beachten!
Teilchenbahn im Magnetfeld:
~L ⊥ ~v ist, bewegt
• Da F
sich geladenes Teilchen
– auf Kreisbahn,
~ ist;
wenn ~v0 ⊥ B
– auf Spiralbahn
andernfalls.
• Lorentz-Kraft =
Zentrifugalkraft:
v0
q<0
2R
FL
Fz
mv 2
qvB =
R
B (in Zeichenebenehinein)
p
mv
=
⇒R=
qB
qB
• Erlaubt Bestimmung vom q/m, z.B. im
Fadenstrahlrohr.
• p = RqB stimmt auch für relativistische Teilchen!
6 Statische magnetische Felder
10. Juni 2009
Kraft auf stromdurchflossene Leiter
Beispiel: gerades Leiterstück
• Betrachte Strom I in
Leiterstück mit Länge L
und Querschnittsfläche A
~
im Magnetfeld B.
FL
I
I = A = nqvA .
• Lorentz-Kraft auf eine
Ladung q:
L
~L = q · (~v × B
~)
F
• Gesamt-Lorentz-Kraft auf
alle Ladungsträger (mittlere
Geschwindigkeit ~v ):
B (in Zeichenebenehinein)
~ ) = I · (L
~L = n V ·q · (~v × B
~ × B)
~
~ ) = I L · (v̂ ×B
F
|{z}
| {z }
=LA
~
=L
Kraft zwischen zwei Strömen:
• Zwei parallele Leiterstücke mit
Strömen I1 , I2 im Abstand d.
• Magnetfeld von Strom I1
L1
am Ort von I2 :
µ0
B1 =
I1
2πd
• Kraft auf Leiter 2:
I1
µ0L2
I1 I2
FL = I2 L2B1 =
2πd
µ0
FL
⇒
I1 I2
=
L2
2πd
• Diese Kraft wird zur Festlegung der
Stromstärkeeinheit Ampère verwendet.
6 Statische magnetische Felder
L2
I2
d
10. Juni 2009
Hall-Effekt
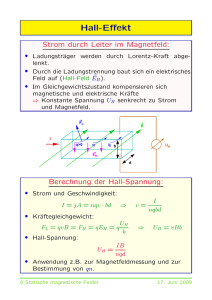
Strom durch Leiter im Magnetfeld:
• Ladungsträger werden durch Lorentz-Kraft abgelenkt.
• Durch die Ladungstrennung baut sich ein elektrisches
~ H ).
Feld auf (Hall-Feld E
• Im Gleichgewichtszustand kompensieren sich
magnetische und elektrische Kräfte
⇒ Konstante Spannung UH senkrecht zu Strom
und Magnetfeld.
FL
B
I
q>0
q
q b
UH
EH
d
Berechnung der Hall-Spannung:
• Strom und Geschwindigkeit:
I = jA = nqv · bd
• Kräftegleichgewicht:
FL = qvB = FH = qEH = q
• Hall-Spannung:
⇒
v=
UH
b
⇒
I
nqbd
UH = vBb
IB
nqd
• Anwendung z.B. zur Magnetfeldmessung und zur
Bestimmung von qn.
UH =
6 Statische magnetische Felder
17. Juni 2009
Stromschleife =
Magnetischer Dipol
Leiterschleife in Magnetfeld:
• Einfachste Konfiguration:
rechteckige Schleife, Strom I,
~
Seite a ⊥ B,
Winkel θ zwischen
~
Seite b und B.
F1
θ’
B
F
4
θ
• Kräfte und Drehmomente:
b
I
~
~
– Seiten b: F2 + F4 = 0,
a
resultierendes
F2
Drehmoment = 0.
~1 + F
~3 = 0,
– Seiten a: F
F3
resultierendes Drehmoment
b
~
~
~
|D | = |F1 | − |F3 | · cos θ = BI a · b cos θ .
2
|{z} | {z }
=A
=sin θ′
• Das magnetische Moment µ
~
ist ein Vektor mit Betrag AI, der senkrecht auf der
~ folgt aus der
Fläche A steht. Die Richtung von µ
Stromrichtung und der rechte-Hand-Regel.
Epot
• Insgesamt: Drehmoment
auf magnetisches Moment
~ =µ
~ .
D
~ ×B
Das Magnetfeld versucht,
den Dipol in Feldrichtung
auszurichten.
0o
−90o
90o
0o
180o
θ’
90o θ’−90o
~
• Wie beim elektrischen Dipolmoment: Epot = −~
µ · B.
6 Statische magnetische Felder
17. Juni 2009
Beispiele magnetischer Dipole
Atomare magnetische Dipolmomente:
• Einfaches Modell:
Elektron (Ladung −e, Masse me )
auf Kreisbahn um Kern.
• Drehimpuls: L = mevr = n~
(QM: Drehimpuls ist gequantelt).
• Magnetisches Moment:
µ=I·A=
• Insgesamt: µ =
L
r
ev
1
· πr2 = evr
2πr
2
q=−e
m=me
e~
·n
2m
|{z}
=µB
• Das Bohrsche Magneton µB ist die natürliche Einheit
atomarer magnetischer Momente.
Drehspulgalvanometer:
• Prinzip:
Stromdurchflossene
Spule im Feld eines
Magneten;
I
• Mechanische
Rückstellkraft, z.B.
durch Spiralfeder;
• Ausschlag
proportional
zum Strom I.
N
S
I
6 Statische magnetische Felder
17. Juni 2009
Die Magnetisierung
Materie im Magnetfeld:
~
Bringt man Materie in ein Magnetfeld B,
so ändert es sich:
~ Vak → B
~ Mat = µB
~ Vak
B
µ = relative Permeabilität;
[µ] = 1
Magnetisierung:
• Definition:
1X
~
µ
~i
Magnetisierung = M =
V V
A
Am2
~
=
[M] =
m3
m
analog zur Definition der elektrischen Polarisation
als “elektrische Dipoldichte”!
n Windungen
mit Strom I
• In vakuumgefüllter Spule:
nIA
nI
= µ0
L
AL
µtot
= µ0
V
⇒ B = µ0 M = µ0
H
|{z}
B = µ0
magn. Erregung
M
A
L
• Für allgemeine Felder mit Materie gilt:
~
~
~
~ Vak + µ0M
~ ;
BMat = µ0 H + M = B
~ Vak = µ0H
~ das von den äußeren Strömen
dabei ist B
erzeugte Feld.
6 Statische magnetische Felder
17. Juni 2009
Magnetische Suszeptibilität,
Magnetismusarten
Magnetische Suszeptibilität:
~ ∝ H:
~
• Im allgemeinen ist M
~ = χm H
~
M
χm = magnetische Suszeptibilität
[χm] = 1
• Damit wird:
~ Mat = µ0 H
~ +M
~ = µ0 (1 + χm ) H
~ = µ0 µH
~ = µB
~
B
| {z }
=µ
Dia-, Para- und Ferromagnetismus:
~ unterscheidet man
Je nach Richtung und Stärke von M
drei Arten von Magnetismus:
Bezeichnung
Suszeptibilität
Permeabilität
Diamagnetismus
χm < 0, |χm| ≪ 1
µ<1
Paramagnetismus
χm > 0, |χm| ≪ 1
µ>1
Ferromagnetismus
χm > 0, |χm| ≫ 1
µ≫1
I
B
I
B
Diamagnet
Paramagnet
F
M
M
F
6 Statische magnetische Felder
24. Juni 2009
Diamagnetismus
• Diamagnetische Materialien bestehen aus
Atomen/Molekülen ohne permanentes
magnetisches Dipolmoment.
Magnetfeld
• Beim Einschalten des
(senkrecht zu
induzierte atomare
Zeichenebene)
Ringströme
~ werden
Magnetfeldes B
atomare Ringströme
induziert (s. Kap. 4.4),
die dem äußeren
Magnetfeld entgegen
wirken.
~ und B
~ sind
• M
antiparallel ⇒ χm < 0
• Im allgemeinen ist
Resultierender
|χm| ≪ 1 und Temperatur- Oberflächenstrom
unabhängig.
Ausnahme:
Supraleiter unterhalb der Sprungtemperatur TC haben
χm = −1, d.h. das Feld wird vollständig aus dem
Material verdrängt (Meißner-Ochsenfeld-Effekt).
Diamagnetische Materialien:
• Typische Werte von χm
(mit Atomgewicht multipliziert):
Material
Helium He
Wasserstoff H2
Stickstoff N2
Wasser H2O
Gold Au
χm · Mm [mol−1]
− 1.9 × 10−9
− 4.0 × 10−9
−12 × 10−9
−13 × 10−9
−28 × 10−9
• Alle Edelgase sind diamagnetisch.
6 Statische magnetische Felder
24. Juni 2009
Paramagnetismus
• Paramagnetische Materialien
bestehen aus Atomen/Molekülen
mit permanentem magnetischen
Dipolmoment.
B=0
• Ohne äußeres Magnetfeld sind
die Dipole wegen der thermischen
Bewegung ungeordnet, d.h. haben
isotrope Richtungsverteilung.
B
• Im Magnetfeld richten sich
die Dipole teilweise
in Feldrichtung aus.
~ und B
~ parallel ⇒ χm > 0.
• In diesem Fall sind M
• Der Grad der Ausrichtung hängt von der Temperatur
ab:
~
h~
µ · Bi
~ = N |~
· B̂
M
µ|
3kT
⇒
χm
~ |
µ0 N µ2
µ0 |M
=
=
~
3kT
|B |
(N = Atome/Volumen,
µ = magnetisches Moment eines Atoms)
Paramagnetische Materialien:
Material
Aluminium Al
Sauerstoff O2
Eisencarbonat Fe CO3
χm · Mm [mol−1 ] (T = 0◦ C)
16.5 × 10−9
3450 × 10−9
11300 × 10−9
• Paramagnetismus ist meist stärker als
Diamagnetismus.
• Auch für paramagnetische Materialien tritt zusätzlich
Diamagnetismus auf!
6 Statische magnetische Felder
24. Juni 2009
Ferromagnetismus
• Ferromagnetische Materialien bestehen aus
Atomen/Molekülen mit permanenten
magnetischen Dipolmomenten.
• Diese Dipole beeinflussen sich über ihr Magnetfeld
gegenseitig und richten sich bevorzugt parallel
zueinander aus.
• Kleine äußere Felder erzeugen große Magnetisierung,
die zum Teil erhalten bleibt, wenn das äußere Feld
abgeschaltet wird.
Hysterese:
M
Hystereseschleife
Remanenz MR
B0= µ 0 H
−Bmax
Bmax
Neukurve
Koerzitivkraft BK
• Die Magnetisierung hängt vom angelegten Feld
~ 0 = µ0H
~ ∝ I ab und von der Vorgeschichte.
B
• Bei zyklischer Variation von H zwischen ±Bmax ergibt
sich Hystereseschleife.
• Remanenz = verbleibende Magnetisierung bei H = 0.
• Koerzitivkraft =
Gegenfeldstärke, bei der wieder M = 0 wird.
6 Statische magnetische Felder
24. Juni 2009
Weißsche Bezirke
Mikroskopische Ordnung:
• In Bereichen der Ausdehnung
10 µm – 1 mm richten sich die
atomaren Dipole parallel aus
(Weißsche Bezirke).
• Diese lokale Ausrichtung
bleibt auch ohne äußeres Feld
bestehen.
~ i in
• Die Orientierung von M
den einzelnen Bezirken ist
ohne äußeres Feld und ohne
Remanenz isotrop.
• Im äußeren Magnetfeld
richten sich die atomaren
Dipole in einem Bezirk
kollektiv aus.
⇒ Die Magnetisierung
steigt in kleinen Sprüngen
an (Barkhausen-Sprünge).
~100 µ m
M
Barkhausen−
Sprünge
B0
Hörbarmachen der Barkhausen-Sprünge:
• Plötzliche Änderung
der Magnetisierung
erzeugt Spannungssignal
in Induktionsschleife
um Magneten.
(Siehe Kap. 4.4).
• Diese Signale
können per
Lautsprecher
hörbar gemacht
werden.
N
6 Statische magnetische Felder
S
Fe
24. Juni 2009
Curie-Temperatur,
einige Ferromagnte
Curie-Temperatur:
• Oberhalb einer bestimmten, materialabhängigen
Temperatur werden Ferromagnete beim Erwärmen
schlagartig paramagnetisch.
• Erklärung:
Die mittlere
χm
kinetische Energie
wird größer als die
potentielle Energie
der Dipol-DipolWechselwirkung.
• Oberhalb von TC ist
χm
1
∝
T − TC
ferromagnetisch
• Diese Temperatur heißt Curie-Temperatur TC .
~
1
T−TC
paramagnetisch
TC
T
Ferromagnetische Materialien:
Material
Eisen Fe
Nickel Ni
Kobalt Co
Gadolinium Gd
Erbium Er
Mumetall (Ni+Cu+Co)
Permeabilität
500 – 10000
80 – 200
TC [K]
1043
627
1385
293
20
100000
• Es gibt weitere ferromagnetische seltene Erden.
• Verschiedene Legierungen haben hohe relative
Permeabilität.
6 Statische magnetische Felder
24. Juni 2009
Das Faradaysche Induktionsgesetz
Experimentelle Beobachtung:
B
An den Enden einer Leiterschleife
wird eine elektrische Spannung Uind A
induziert, wenn sich der
magnetische Fluss durch die
von der Leiterschleife
umschlossene Fläche A ändert:
I
~ dA
~ 6= const.
B
A
⇔
Uind 6= 0
Uind
Faradaysches Induktionsgesetz:
I
dΦm
d
~
~
B dA = −
Uind = −
dt
dt
A
A
• Vorzeichen:
“Richtung der Messung von Uind”
C
→ Umlaufsinn um Leiterschleife
~ nach
−+
→ Richtung von dA
Uind >0
der rechte-Hand-Regel.
• Flussänderung dΦm /dt kann verursacht werden von
~ (z.B. Einschalten von Magnet);
– Änderung von B
– Änderung von A (z.B. Verformung der Schleife);
~ A)
~ (z.B. Drehung).
– Änderung von ∢(B,
H
~ d~s = Uind
• Wegintegral E
Wegintegral über geschlossenenen Weg ist ungleich
~
Null! Zeitabhängige E-Felder
sind nicht konservativ.
7 Zeitabhängige elektromagnetische Felder
24. Juni 2009
Induktionsbeispiele
Rotierende Leiterschleife:
• Bei konstanter
Winkelgeschw. ω:
φ
A
Φm = AB cos φ
= AB cos(ωt + φ0)
B
ω
• Induktionsspannung:
dΦm
dt
= −AB [−ω sin(ωt + φ0)]
= ABω sin(ωt + φ0 )
Uind = −
Uind
(Wechselspannung)
• Prinzip des Generators.
Spule mit Induktionsschleife:
• Magnetischer Fluss
in Spule mit
N Windungen:
L
2R
N Windungen,
Strom I(t)
A
Φm = AB
= πR2 · µ0
N
· I(t)
L
• Spannung in
Induktionsschleife
(eine Windung):
Uind
Uind
dΦm
µ0πR2 N dI(t)
=−
=−
·
dt
L
dt
7 Zeitabhängige elektromagnetische Felder
24. Juni 2009
Selbstinduktion, Einschaltvorgang
Selbstinduktion:
• Beim Einschalten des Stroms in einer Spule
(Länge ℓ, N Windungen) induziert die
Flussänderung in der Spule eine Spannung Uind
in der Spule selbst.
• In N Windungen ist Uind N mal so groß wie in einer
einzelnen Induktionsschleife:
Uind
dΦm
µ0AN 2 dI(t)
= −N
=−
·
dt
ℓ
dt
• Eine induzierte Spannung tritt bei Stromänderungen
in allen stromführenden Anordnungen auf, mit
Uind = −L ·
dI(t)
dt
Vs
= Henry = H
A
µ0 AN 2
• Selbstinduktivität einer Spule: L =
.
ℓ
L = Induktivität;
[L] =
Einschaltvorgang:
S
• Stromkreis mit L, R und U0 :
U0 = RI − Uind
U0
dI
= RI + L
dt
• DG für I(t) mit Lösung
U0 −(R/L)t
I(t) =
1−e
R
I
I 0=Uo/R
L
R
0.63I0
• Zeitkonstante des
Stromanstiegs: τ = L/R
7 Zeitabhängige elektromagnetische Felder
t
τ
24. Juni 2009
Die Lenzsche Regel
Vorzeichen von Induktionsspannungen:
Das negative Vorzeichen im Induktionsgesetz hat eine
generelle Konsequenz für alle Induktionseffekte:
Die durch Induktion bewirkten
Spannungen, Ströme und Felder
wirken stets dem die Induktion
verursachenden Vorgang entgegen.
Beispiel:
Bind
F
Iind
v
• Permanentmagnet bewegt sich auf Spule zu.
• Durch die Änderung des magnetischen Flusses
wird in der Spule eine Spannung Uind induziert,
durch die ein Strom Iind erzeugt wird.
~ ind .
• Der Strom erzeugt ein Magnetfeld B
~ ind wirkt der Flusszunahme
Lenzsche Regel: B
in der Spule entgegen, ist also dem Feld des
Permanentmagneten entgegengerichtet.
• Es resultiert eine abstoßende Kraft zwischen Spule
und Magnet.
7 Zeitabhängige elektromagnetische Felder
01. Juli 2009
Ausschaltvorgang
Abkoppeln der Spannungsversorgung
von einem Stromkreis mit Induktivität:
• Vor Öffnen des Schalters S
(lange nach Einschalten):
S
I1 = U0 /R1
IL = U0 /RL = I0
U0 R1
I
L,RL
• Nach Öffnen des Schalters S:
0 = RI − Uind = RI + L
dI
dt
(mit R = R1 + RL ).
• DG für I(t) mit Lösung
I
I 0=Uo/RL
I(t) = I0 · e−(R/L)t
• Die Induktion bewirkt einen
Strom, der das Magnetfeld
in der Induktivität
aufrechtzuerhalten versucht.
• Induktionsspannung an L:
Uind = −L
t
R1 + RL −(R/L)t
dI
= U0
e
.
dt
RL
Falls R1 ≫ RL ist, wird Uind ≫ U0
• Praktische Konsequenzen:
– Bei Ausschaltvorgängen entstehen u.U. hohe
Spannungsspitzen, die elektrische/elektronische
Geräte beschädigen können.
– Diese Spannungsspitzen werden z.B. zum Zünden
der Gasentladung in Leuchtstoffröhren
verwendet.
7 Zeitabhängige elektromagnetische Felder
01. Juli 2009
Energieinhalt des Magnetfeldes
Energie des Magnetfeldes:
• Der Strom I(t) nach dem Ausschalten erzeugt im
Widerstand R = R1 + RL Joulesche Wärme, die
gleich der im Magnetfeld gespeicherten Energie ist:
Wm = R
Z∞
I 2 (t) dt = RI02
0
L −(2R/L)t
−
e
2R
∞
0
=
1 2
I0 L
2
• Für eine Spule (Querschnitt A, Länge ℓ) ist die
magnetische Energiedichte
wm
2
1 2
1
Wm
2A 1
2N
= I0 µ0N
= µ0 I0 2
=
V
2 | {z ℓ} |{z}
Aℓ
2
ℓ
=L
=1/V
Mit B0 = µ0 I0 N/ℓ wird
wm =
1 2
B0
2µ0
Zusammenfassung
elektromagnetischer Energien:
1 2
1
2
Wm = LI
Wel = CQ
2
2
 
1

2 + 1 B2

ohne Materie
ǫ
E

2 0
µ0
welm =


1


mit Materie
 [ED + BH ]
2
7 Zeitabhängige elektromagnetische Felder
01. Juli 2009
Generator und Elektromotor
Funktionsprinzip
Rotierende Leiterschleife bzw. Spule im äußeren
Magnetfeld:
Generator:
Elektromotor:
Mechanischer Antrieb
↓
Rotation
↓
Induzierte Spannung
↓
Elektrische Leistung
Angelegte Spannung
↓
Strom in Spule
↓
Drehmoment auf Spule
↓
Mechanische Leistung
Kontinuierliche Drehung des Motors erfordert
Umpolen des Stroms oder des Magnetfeldes.
S
ω
Wechselstrommotor:
Dreht sich mit
Frequenz der
angelegten
Wechselspannung.
B
N
U= U0sin(ω t)
7 Zeitabhängige elektromagnetische Felder
01. Juli 2009
Gleichspannungsmotor und
Gleichspannungsgenerator
Funktionsprinzip:
• Umpolen der
zur
Stromrichtung in Kontakte
Drehspule
Isolator
der Drehspule
(Rotator) durch
segmentierte
Schleifkontakte
an der Drehwelle
(Kommutator).
Kohlestifte
• Funktioniert
unabhängig
U
von Drehfrequenz.
+ −
• Elektromotor: Betrieb mit Gleichspannung.
• Generator: Liefert Spannung mit festem Vorzeichen.
Technische Verbesserungen:
• Verwendung von N Spulen,
2
1
B
deren Drehwinkel um
π/N gegeneinander
3
versetzt sind:
– Erfordert meherere
Spulen
Kommutatoren oder
mehr Segmente an
Drehachse
einem Kommutator.
U
– Generator: Glattere
Beispiel: N=2
Ausgangsspannung.
1+2
– Elektromotor:
runderer Lauf.
• Rotator mit Eisenkern
1
2
t
7 Zeitabhängige elektromagnetische Felder
01. Juli 2009
Wechselstrom und -spannung
Wechselstrom bzw. Wechselspannung hat eine
harmonisch oszillierende Zeitabhängigkeit, z.B.:
U (t) = U0 cos(ωt)
U
U0 = Amplitude
U0
ω = Kreisfrequenz
2π
=
= 2πν
T
T = Periodendauer−U
0
1
= Frequenz
ν=
T
t
0
T
Wechselstrom durch Widerstand R:
R
I~
U~
U (t) = U0 cos(ωt)
U (t)
U0
I(t) =
=
cos(ωt)
R
R
|{z}
=I0
P (t) = Leistung = U (t) · I(t)
= U0 I0 cos2 (ωt) ≥ 0
• Mittlere Leistung hP i =
1
T
ZT
P (t) dt =
0
1
U0 I0.
2
• Effektive Spannung, effektiver Strom:
U0
Ueff = √ ,
2
I0
Ieff = √
2
⇒
hP i = Ueff · Ieff .
• Netzspannung (D): Ueff = 230 V, ν = 50 Hz .
7 Zeitabhängige elektromagnetische Felder
08. Juli 2009
Wechselstromkreise mit C oder L
Wechselstrom durch
Kapazität C:
U (t) = U0 cos(ωt) =
I(t) =
Q
C
dQ
= − CU
| {z0ω} sin(ωt)
dt
C
I~
U~
U
=I0
t
P (t) = Leistung = U (t) · I(t)
= −U0 I0 cos(ωt) sin(ωt)
I
• Strom und Spannung um +90◦ phasenverschoben
(Spannung eilt voraus).
• Mittlere Leistung: hP i = 0.
• “Wechselstromwiderstand” U0 /I0 = 1/ωC nimmt mit
steigendem ω ab.
Wechselstrom durch
Induktivität L:
L
dI
U (t) = U0 cos(ωt) = L
dt
Z
U0
I(t) =
cos(ωt)
L
U0
sin(ωt)
=
ωL
|{z}
I~
U~
U
I
t
=I0
• Strom und Spannung um −90◦ phasenverschoben
(Strom eilt voraus).
• Mittlere Leistung: hP i = 0.
• “Wechselstromwiderstand” U0/I0 = ωL nimmt mit
steigendem ω zu.
7 Zeitabhängige elektromagnetische Felder
08. Juli 2009
Wechselstromkreis mit L, C und R
Wechselstrom durch L, C und R:
C
U (t) =U0 cos(ωt)
Q
;
C
I(t) =I0 cos(ωt − φ) ;
=RI + LI˙ +
U̇ (t) = − U0ω sin(ωt)
I
=RI˙ + LI¨ +
C
I~
R
L
U~
1
= − RI0 ω sin(ωt − φ) − LI0ω 2 − I0 cos(ωt − φ) ;
C
• Beiträge von L, C und R zur Gesamtspannung haben
Phasenverschiebungen von 90◦ relativ zueinander.
Zeigerdiagramm:
• Darstellung der
y
U (t)–Beiträge mit
ω
Hilfe von Vektoren
ωL
(“Zeigern”), die mit ω
in der (x, y)-Ebene L−1/ ω C
Z
ω
φ
x
rotieren, so dass
R
Projektion auf
1/ ω C
x-Achse U (t) ergibt.
• Länge der Zeiger: U/I0 .
• Summenzeiger Z; |Z| = Impedanz; [Z] = Ω.
• R zeigt nach rechts (phasengleich mit I)
⇒ Z ergibt Phasenverschiebung von U (t) und I(t).
U0
U0
I0 =
=q
|Z|
R2 + ωL −
1 2
ωC
;
7 Zeitabhängige elektromagnetische Felder
tan φ =
ωL −
R
1
ωC
.
08. Juli 2009
Der Schwingkreis
Stromkreis mit C, L und R
ohne treibende Spannung:
• Schalter S in Stellung 1:
Aufladen von C.
• Umschalten auf Stellung 2:
+
C entlädt sich, Strom I. U −
I
=0
LI¨ + RI˙ +
C
1
S
R
2
I~
C
L
• Diese Differentialgleichung ist mathematisch
äquivalent zur Differentialgleichung für eine
gedämpfte Schwingung: mẍ + kẋ + Dx = 0
(k = Reibungskoeffizient, D = Federkonstante).
• Lösungen wie bei mechanischer Schwingung mit den
Ersetzungen m → L, k → R, D → 1/C:
– Gedämpfte Schwingung (R2 < 4L/C):
I(t)
R
t)
I(t) = I0 cos(ωt) · exp(− 2L
q
1
−
ω = LC
t
R2
4L2
Sonderfall: Ungedämpfte Schwingung für R = 0.
– Aperiodischer Grenzfall (R2 = 4L/C)
– Kriechfall (R2 > 4L/C)
• Bei Anregung mit Spannung U (t) = U0 cos(ωt) bilden
sich erzwungene
Schwingungen aus (Resonanz bei
√
ωR = 1/ LC).
7 Zeitabhängige elektromagnetische Felder
08. Juli 2009
Der Tesla-Transformator
Funktionsprinzip:
Transformator mit großen Windungsverhältnis N2/N1 ,
der durch hochfrequente Stromstöße angeregt wird.
N2 Sekundärwindungen
Ui
Ua
C
F
N 1 Primär−
windungen
Erklärung:
• Der Kondensator C wird mit Ui (Gleichspannung,
niederfrequente Wechselspannung) aufgeladen.
QC
• Übersteigt die Spannung
an der Funkenstrecke F
Aufladen
einen bestimmten Wert,
Entladen
wird C über einen Funken
t
entladen. Dieser Vorgang
wiederholt sich zyklisch.
~1ms
• Dabei fließt ein hoher Strom,
T
der in sehr kurzer Zeit abklingt.
• Große Flussänderung dΦm /dt ⇒ Ausgangsspannung
bis zu Ua = O(100 kV), besonders wenn die Frequenz
1/T der Auf/Entladezyklen im Primärkreis auf die
Sekundärkreis-Resonanzfrequenz abgestimmt ist.
• Medizinische Anwendung: Deposition von
Joulescher Wärme in tieferen
Gewebeschichten (Diathermieströme).
7 Zeitabhängige elektromagnetische Felder
08. Juli 2009
Wellenlänge, Wellenzahl,
Lichtgeschwindigkeit
Harmonische Welle:
~
• Das E-Feld
– macht harmonische Schwingung ∝ sin[ωt + φ(~
r)]
an jedem Punkt im Raum;
– variiert bei festem t sinusförmig entlang z
• Wellenfronten = Orte gleicher Phase:
Ebenen senkrecht zur Ausbreitungsrichtung ẑ
E
c
t=T/4
z
t=0
Wellenlänge λ
Lichtgeschwindigkeit:
• Frequenz ν, Schwingungsperiode T : ν = ω = 1
2π
T
2π
• Wellenzahl k, Wellenlänge λ: k =
λ
• Ausbreitungsgeschwindigkeit der Wellenfronten:
ωλ
ω
λ
= νλ =
=
T
2π
k
• Vergleich mit k2 = ǫ0 µ0ω 2 ergibt:
c=
c = Lichtgeschwindigkeit = √
1
= 2.998 × 108 m/s
ǫ0µ0
• In Materie: cMat = cVak /√ǫµ (ν-abhängig).
8 Elektromagnetische Wellen
15. Juli 2009
Spektrum
elektromagnetischer Wellen
Die Frequenz ν und die Wellenlänge λ = c/ν
elektromagnetischer Wellen variieren über einen riesigen
Bereich (bekannt: mehr als 24 Größenordnungen)
Photon−
Energie [eV]
Frequenz [Hz]
Wellenlänge λ
[m]
Sichtbares Licht:
1010
108
106
104
2
24
10
22
10
20
10
1018
10
1016
1
14
10−2
10−4
−6
10
10−8
10−10
Gamma−
strahlung
Röntgen−
strahlung
Ultraviolett
λ [nm]
10−14
390
10−12
−10
10
10−6
Infrarot
10−4
10
−2
1010
Mikrowellen
10
Radiowellen
10
10
blau
492
10
grün
gelb
577
592
orange
622
102
104
4
2
455
1
108
6
violett
10−8
Sichtbar
10
12
10−16
Ultra−
langwellen
1
106
108
rot
780
Die Energie elektromagnetischer Wellen ist gequantelt:
E = hν = 6.626 × 10−34 J/s · ν.
Hohe E: elm. Strahlung hat teilchenartigen Charakter.
8 Elektromagnetische Wellen
15. Juli 2009
Hertzscher Dipol (I)
Stehende Wellen in offenem Schwingkreis:
• Harmonisch oszillierende Ströme und Spannungen in
einem offenen Schwingkreis (Metallstab) entsprechen
stehender Welle:
t=0
t=T/4
t=T/2
t=3T/4
+
0
−
0
U(t)
Imax
I=0
L
Imax
I=0
I(t)
0
−
+
0
• Stabenden:
Knoten von I, Bäuche von U
Stabmitte:
Bauch von I, Knoten von U .
• Resonanzbedingung:
λDipol = 2L
⇒
ωR =
2πcDipol
c
π
= ·√
λDipol
L
ǫµ
Achtung: ǫµ ist frequenzabhängig, z.B. ist für Wasser
ǫ(ν = 0) = 81, aber ǫ(Licht) ≈ 2.
Abgestrahlte Welle:
• Der oszillierende Strom im Dipol erzeugt eine
elektromagnetische Welle mit Wellenlänge
2πc
√
= 2L ǫµ
ωR
• Länge einer Sendeantenne ist L = O(λ)
⇒ hohe Sendemasten für λ = 1 . . . 104 m (Radio).
λ=
8 Elektromagnetische Wellen
15. Juli 2009
Hertzscher Dipol (II)
Abgestrahlte Leistung:
p2ω 4 sin2 θ
hPemi =
32π 2 ǫ0c3 r2
Hertz−Dipol
Beobachter
θ
r
• hPemi ∝ 1/r2
Gesamte Strahlungsleistung unabhängig vom
Abstand vom Sender ⇒ Strahlung trägt Energie weg.
2
• hPemi ∝ sin2 θ
I(θ)~sin ( θ )
θ
Dipol
(max. Dipolmoment p)
Maximale Intensität senkrecht zum Dipol,
keine Abstrahlung in Dipol-Richtung.
• hPemi ∝ ω 4
Intensität nimmt mit ω 4 ∝ 1/λ4 zu
(erklärt z.B. die blaue Himmelsfarbe).
Empfangscharakteristik:
r
2
hPempfi ∝ hPSender i · sin α
sin θ sin α 2
∝
r
θ
α
Empfänger
Sender
8 Elektromagnetische Wellen
15. Juli 2009
Polarisation
~
Schwingungsrichtung des E-Vektors:
Polarisation bezeichnet bestimmte Konfigurationen der
~
Schwingungsebene des E-Vektors
senkrecht zur
Ausbreitungsrichtung der Welle
• Lineare Polarisation:
~
E-Vektor
schwingt in einer festen Ebene,
~
B-Vektor schwingt in der dazu orthogonalen Ebene.
Beispiel: Welle von einem Hertzschen Dipol.
• Zirkulare Polarisation:
~ und B
~ “rotieren” um die Ausbreitungsrichtung
E(B, t=T/4)
E
cB
t=T/4
t=T/4
E
t=0
t=0,t=T/2
(B, t=0)
t=3T/4
t=T/4
t=3T/4
(B, t=T/2)
t=T/2
t=3T/4
(B, t=3T/4)
linear polarisiert
zirkular polarisiert
• Überlagerung (Superposition) von Wellen kann
Polarisation ändern, z.B.:
– linear + linear → zirkular;
– links-zirkular + rechts-zirkular → linear.
Erzeugung und Nachweis von Polarisation:
• Metallgitter absorbiert
~ parallel
Welle, wenn E
zu Gitterstäben ist.
~ Gitter) = φ
• Bei ∢(E,
Sender
kommt E sin φ durch
⇒I ∝ sin2 φ.
8 Elektromagnetische Wellen
E
φ
E
15. Juli 2009
Lichtstrahlen und Brechungsindex
Lichtstrahlen:
• Lichstrahlen sind
Ausschnitte aus
ebenen Lichtwellen,
d»λ
die sich gebündelt
und parallel ausbreiten.
c
• Dies ist eine idealisierte
Annahme, die nur für
Strahldurchmesser ≫ λ näherungsweise richtig ist.
• Beispiele:
Laser-Strahl, Lochblende und Linse hinter Lampe
• Eigenschaften:
– Lichtstrahlen breiten sich im homogenen Medium
geradlinig aus.
– Die Wege von Lichtstrahlen sind umkehrbar.
• Beschreibung der Ausbreitung von Lichtstrahlen in
der geometrischen Optik.
Der Brechnungsindex:
Ausbreitungsgeschwindigkeit von Licht in Medium:
cVakuum
cVakuum
cMedium = √
=
ǫµ
n
n = Brechungsindex = n(ν) ; [n] = 1
Brechungsindices einiger Materialien
(λ = 589 nm):
◦
Luft (20 C, Normaldruck) 1.00028
Wasser
1.333
1.458
Quarzglas
2.417
Diamant
9 Geometrische Optik
15. Juli 2009
Das Brechungsgesetz
Brechung und Reflexion:
• An einer Grenzfläche
zwischen zwei Medien mit
Brechungsindices n1 und
n2 spaltet sich ein
einfallender Strahl auf:
[E] Einfallender Strahl
[R] Reflektierter Strahl
[B] Gebrochener Strahl
• Einfalls-, Reflexions- und
Brechungswinkel werden
bzgl. der Flächennormalen
gemessen.
E
n1
R
α α’
β
n2
B
Das Snelliussche Brechungsgesetz:
• Die einlaufende
Wellenfront legt
Weg x1 zurück,
während die
gebrochene
Wellenfront
x2 durchläuft:
c
∆t = L sin α
x1 =
n1
c
∆t = L sin β
x2 =
n2
n2
sin α
=
⇒
sin β
n1
L
n1
α
α
β
x2
β
x1
n2
• Der Strahl wird im dichteren Medium zur Normale
hin gebrochen, im dünneren Medium davon weg.
9 Geometrische Optik
22. Juli 2009
Reflexion und Totalreflexion
Das Reflexionsgesetz:
• Einfallender und
reflektierter Strahl
haben gleiche
Ausbreitungsgeschwindigkeit.
• Die Dreiecke
ABD und BAD
sind kongruent:
α = α′
Einfallswinkel =
Ausfallswinkel
D
C
n1
α’
α
α’
α
A
B
x1
n2
Totalreflexion:
• Bei Auftreffen auf
optisch dünneres
Medium (n2 < n1):
n2
sin β
sin α =
n1
n2
<
<1
n1
• Für Einfallswinkel
sin α > n2/n1 = sin αT
γ
β
α
n1>n2
α < αT
β = αT
γ > αT
n2
gibt es keinen
gebrochenen Strahl.
• In diesem Fall erfolgt Totalreflexion, d.h. die gesamte
Intensität des Strahls wird reflektiert.
• Anwendung:
Z.B. Lichtleitung in Glasfasern.
9 Geometrische Optik
22. Juli 2009
Spiegel und Bildentstehung
Reflexion an ebenem Spiegel:
• Jeder von einem Punkt P
ausgehende Lichtstrahl
wird entsprechend dem
Reflexionsgesetz
reflektiert.
P
• Für Betrachter vor dem
Spiegel kommen die Strahlen
scheinbar von einem
gemeinsamen Punkt P ′
hinter dem Spiegel.
P’
Spiegel
Bildentstehung:
• Prinzip:
Wenn sich alle von
einem Punkt eines
Gegenstandes G
G
ausgehenden Strahlen
in einem anderen Punkt
treffen, entsteht dort
ein vom Betrachter
gesehenes Bild B
des Gegenstandes.
B
• Bei einem Spiegel ist
Spiegel
dieses Bild
– aufrecht;
– virtuell, d.h. die Lichtstrahlen erreichen den Ort
des Bildes nicht;
– genauso groß wie der Gegenstand.
9 Geometrische Optik
22. Juli 2009
Der sphärische Hohlspiegel
Brennpunkt und Brennweite:
• Brennpunkt:
Punkt F , in den
achsenparallele
Strahlen fokussiert
werden.
S
α
α
R
h
M
α
F
• Brennweite:
Abstand F – Spiegel
1
f =R 1−
2 cos α
f
R
Spiegel
• Paraxiale Näherung:
Achsennahe Strahlen (h ≪ f, R) ⇒ f ≈ R/2
Abbildungsgleichung:
• Vergleich ähnlicher
Dreiecke:
DCF mit DC’S1
AA’F mit FES2
B+G
B
=
b−f
b
G
B
=
g−f
f
g
A
S1
C’
G
• Daraus folgt die
Abbildungsgleichung
(paraxiale Näherung):
C
A’
B
D
F
E
S2
b
f
Spiegel
1
1
1
= +
f
b
g
9 Geometrische Optik
22. Juli 2009
Dünne Linsen
Rotationssymmetrische Körper aus durchsichtigem
Material (Glas, Kunststoff) mit sphärischen oder
ebenen Oberflächen.
R2<0
R1<0
Licht
bikonvex
(Sammellinse)
R2>0
R2<0
bikonkav
(Zerstreuungslinse)
R1 =
8
R1>0
plan−konvex
Vorzeichenkonvention für Krümmungsradien:
R > 0 für konvexe Oberflächen;
R < 0 für konkave Oberflächen
(in Lichtrichtung gesehen).
Brennpunkt und Brennweite:
• Paraxiale Strahlen werden von
Linsen in einen Brennpunkt F
fokussiert.
• Aus Brechnungsgesetz und
Geometrie der sphärischen
Oberflächen:
Linsen−
ebene
F
f = Brennweite
1
R1 R2
=
·
n − 1 R2 − R1
[für R1 = −R2:
f = (R/2)/(n − 1)]
f
D
• Dünne Linsen: Linsendicke D ≪ f .
• Für dünne Linsen ist die Brennweite für beide
Durchstrahlungsrichtungen gleich.
9 Geometrische Optik
22. Juli 2009
Abbildungen durch dünne Linsen
Sammellinse, g > f :
Linsen−
ebene
A
b
L2
G
F1
O
D
E
B
F2
L1
g
reelles,
kopfstehendes
Bild
C
f
• Abbildungskonstruktion: wo treffen sich Strahlen, die
von einem Punkt des Gegenstandes ausgehen?
• Reelles Bild: Strahlen treffen sich wirklich;
Virtuelles Bild: Fortsetzungen der Strahlen jenseits
der Linsenebene treffen sich.
• Aus Vergleich der Dreiecke ADF2 mit L1OF2
und CEF1 mit L2L1C (wie beim Hohlspiegel):
B
B+G
=
b−f
b
B
G
= ;
g−f
f
Sammellinse, g < f :
1
1
1
= + .
f
g
b
⇒
Zerstreuungslinse:
Linsen−
ebene
Linsen−
ebene
B
F1
G
G
F1
B
F2
F2
f
−f
−b
virtuelles, aufrechtes Bild (B>G)
g > 0,
virtuelles,
aufrechtes
Bild (B<G)
−b
g
f > 0,
9 Geometrische Optik
b<0
g
g > 0,
f < 0,
b<0
22. Juli 2009
Abbildungsmaßstab, Linsensysteme
Abbildungsmaßstab:
• Vorzeichenkonvention:
G>0
B > 0, wenn das Bild kopfstehend ist.
• Lateralvergrößerung:


< 0
f
B
= >0
M =− =

G
f −g
= ∞
wenn g > f
wenn g < f
wenn g = f
Linsensysteme:
L
G
F12
B
F22
F11
B1
F21
f1
g1
f2
g2
f1
f2
b1
b2
• Prinzip der Abbildungskonstruktion:
Das Bild der ersten Linse bildet den Gegenstand der
zweiten Linse (egal ob reell oder virtuell).
• Gegenstandsweite des Systems: g = g1;
Bildweite des Systems: b = b2
1
1
1
1
L
1
+ = =
+
−
b
g
f
f1
f2 f1 f2
L≪f1 ,f2
≈
1
1
+
f1
f2
• Die inverse Brennweite nennt man Brechkraft:
D∗ = 1/f ;
9 Geometrische Optik
[D∗] = m−1 = Dioptrie = dpt .
22. Juli 2009
Abbildungsfehler
Abbildungsfehler: Effekte, die dazu führen, dass das
Bild eines Gegenstandes unscharf oder verzerrt ist.
1. Chromatische Abberation:
Linsen−
Die Frequenzabhängigkeit
ebene
des Brechnungsindexes
(Dispersion) führt zu
unterschiedlichen
Brennweiten für Licht
unterschiedlicher Farbe.
⇒ Bild ist nur für einen
fb
schmalen Farbbereich scharf.
2. Spärische Abberation:
fr
Achsenferne Strahlen
Linsen−
ebene
werden nicht in Brennpunkt
fokussiert (Verletzung der
paraxialen Näherung).
⇒ Äußere Bildbereiche
unscharf.
3. Koma:
Schräg einfallendes Licht
∆f
wird von verschiedenen
Linsen−
ebene
Bereichen der Linse auf
verschiedene Punkte
fokussiert.
⇒ Bild wird unscharf,
wenn Linse schräg steht.
4. Astigmatismus:
Unterschiedliche Fokalebenen der horizontalen und
vertikalen Querschnitte von Lichtkegeln.
⇒ Stäbchenförmige Verzeichnung.
5. Bildfeldwölbung, Verzeichnung
Scharfes Bild entsteht auf einer gekrümmten Fläche,
bei Abbildung in Ebene entsteht Verzerrung.
9 Geometrische Optik
22. Juli 2009
Das Auge
Das Auge - ein optisches Instrument:
• Linse: fokussiert des
Licht auf die Netzhaut,
Linse
kann durch Muskeln
verformt und damit in der
Brennweite verändert
werden. Bei parallel
einfallendem Licht (g = ∞)
Iris
ist das Auge entspannt. (Blende)
• Iris: verstellbare
Lochblende (Pupille).
• Netzhaut: Bildfläche.
Netzhaut
Glas−
körper
22mm
Sehwinkel und deutliche Sehweite:
• Ein Objekt wird umso
größer wahrgenommen,
G
ε0
desto größer der Winkel ǫ0
zwischen den Randstrahlen
des Objekts ist.
s=g
• Bei Abstand s zwischen Auge
und Objekt ist tan(ǫ0 /2) = G/2s.
• Maximales ǫ0 bei entspanntem Auge für
deutliche Sehweite s0 ≈ 25 cm
(darunter kann das Auge nicht scharf stellen).
• Mit tan(ǫ0/2) ≈ ǫ0/2 wird ǫ0 = G/s0
Sehfehler
Kurzsichtigkeit,
Korrektur durch Zerstreuungslinse
9 Geometrische Optik
Weitsichtigkeit,
Korrektur durch Sammellinse
22. Juli 2009
Die Lupe, Winkelvergrößerung
Die Lupe:
• Kurzbrennweitige Sammellinse,
wird optimal so gehalten, dass das Objekt in der
Brennebene liegt (g = f ) und der Abstand
Lupe–Auge ebenfalls f ist:
ε
G
f
f
• In dieser Anordnung erreicht paralleles Licht das Auge
(Auge ist entspannt).
• Sehwinkel: ǫ ≈ G/f
Winkelvergrößerung:
• Die Vergrößerung V optischer Instrumente wird als
Verhältnis des Sehwinkels mit und ohne Instrument
gemessen:
V =
Sehwinkel ǫ mit Instrument
Sehwinkel ǫ0 mit bloßem Auge bei s0
• Für die Lupe erhält man:
V =
9 Geometrische Optik
s0
G s0
ǫ
=
=
ǫ0
f G
f
22. Juli 2009
Mikroskop und Teleskop
Mikroskop:
• Zwei kurzbrennweitige Sammellinsen,
Bild von Linse 1 in Brennebene von Linse 2:
L=b1+f2
F22
F11
G
F12
F21
B1
f1
g
ε
f1
f2
b1
Objektiv
f2
Okular
• Sehwinkel: ǫ ≈ tan ǫ = B1 /f2 = Gb1/(gf2 )
• Winkelvergrößerung:
V =
s0 b1
s0 (L − f2 )
s0(L − f2 )
ǫ
=
=
≈
ǫ0
gf2
gf2
f1 f2
Teleskop:
L=f1 +f2
F11
F22
ε0
F21
B1
ε
f 1 , b1
Objektiv
9 Geometrische Optik
f2
f2
B
;
f2
B
ǫ0 ≈
f1
ǫ
f1
V =
=
.
ǫ0
f2
ǫ≈
Okular
22. Juli 2009