Beobachter
Werbung

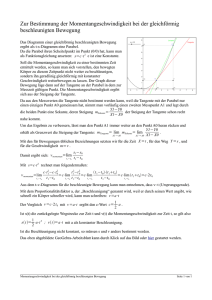
Beschl. Bewegung & Paradoxa in der SRT ARNE BAHR Gliederung Beschleunigte Bewegung Paradoxa • Gleichförmig beschl. Beobachter • Einschränkungen in der Größe eines beschl. Bezugssystems • Fermi-Walker Tetrade • Lokales Koordinatensystem Beobachters • Zwillingsparadoxon • Maßstabsparadoxon • Das Wichtige auf einer Folie Kurze Einführung in die SRT Metrik: Pseudo Skalarprodukt: Summenkonvention Lorentz-Transformationen: Metrik als Abb. In den Dualraum: Vektor Dualer Vektor Kontravariant Kovariant Kurze Einführung in die SRT Metrik: Linienelement: Vierergeschwindigkeit Viererbeschleunigung Zeitdilatation: Längenkontraktion: Beschleunigte Bewegung Gleichförmig beschleunigter Beobachter Gleichförmig beschleunigter Beobachter Man kann zeigen: Wir wollen: Gleichförmig beschleunigter Beobachter: Zusammenfassung • • • Hyperbelgleichung Gleichförmig beschleunigter Beobachter: Zusammenfassung Horizont II Empfangen Senden I Ja Ja II Nein Ja III Nein Nein IV Ja Nein III I IV Einschränkungen bezgl. der Größe eines beschl. Bezugssystems Größenbeschränkung eines beschleunigten Bezugssystems Konstant beschleunigter Beobachter: Beobachter Empfangen Senden I Ja Ja Kausalzusammenhang II Nein Ja Sichtbar; Kann nicht sehen III Nein Nein Nicht sichtbar; Kann nicht sehen IV Ja Nein Nicht sichtbar; Kann sehen Größenbeschränkung eines beschleunigten Bezugssystems Beobachter in Ruhe Beobachter in Ruhe Beschleunigte Phase Größenbeschränkung eines beschleunigten Bezugssystems • Instantanes Ruhesystem • Inkonsistent ab Entfernungen (Überlapp der Koordsyst.) Natürliche Lösung in direkter Umgebung: Fermi-Walker transportierte Tetrade Fermi-Walker transportierte orthonormale Tetrade TETRADE EINES GLEICHFÖRMIG BESCHLEUNIGTEN BEOBACHTERS Tetrade eines gleichförmig beschleunigten Beobachters wählen Schöner: sodass (1) orthogonal (2) nicht rotierend Tetrade eines gleichförmig beschleunigten Beobachters Schöner: wählen sodass (1) orthogonal (2) nicht rotierend Lorentz-Transformation in xRichtung, sodass . Orthogonalität und Einheitslänge: „Nicht rotierend“ Fermi-Walker transportierte orthonormale Tetrade TETRADE EINES BELIEBIG BESCHLEUNIGTEN BEOBACHTERS Tetrade eines beliebig beschleunigten Beobachters Lorentz-Transformation in xRichtung, sodass . Orthogonalität und Einheitslänge: Tetrade soll „nicht rotieren“ Keine Rotation in ℝ3 Pseudorotation im 𝕄4 ändert Richtung! Drehung im ℝ3 Orthogonal zu ω mit Endliche Beschleunigung: Tetrade eines beliebig beschleunigten Beobachters Drehung im ℝ3 Orthogonal zu ω Analog im 𝕄4 : mit mit antisym. Längeninvarianz: sym. Infinitesimale Lorentz-Transformation muss: (1) Entsprechende Lorentz-Trafo. in der (2) Keine Rotation in anderen Ebenen -Ebene generieren Eindeutige Lösung: Tetrade eines beliebig beschleunigten Beobachters Fermi-Walker Transport: Natürliche Bezugssystem eines beschleunigten Beobachters: • 4 orthogonale, Fermi-Walker transportierte (entlang der Weltlinie) Vektoren • Einer entspricht der Vierergeschwindigkeit Lokales Koordinatensystem eines beschleunigten Beobachters Lokales Koordinatensystem eines beschleunigten Beobachters Verschiebungsvektor 𝒫( ) Position des Beobachters Raumartige Basisvektoren Raumartige Hyperflächen festgelegt durch 𝒫( ) und 𝒫( ) Punkt auf der Hyperfläche: „Euklidische Koordinaten“ Lokales Koordinatensystem eines beschleunigten Beobachters „Euklidische Koordinaten“ Tetrade des Beobachters Rindler-Koordinaten Lokales Koordinatensystem eines beschleunigten Beobachters Rindler-Koordinaten Paradoxa Paradoxon Annahme Realität ist in sich konsistent physikalisches Paradoxon Widerspruch in einer Theorie Artefakt eines Fehlers Theorie falsch Zwillingsparadoxon Maßstabsparadoxon Längenkontraktion: Sei so groß, dass Maßstabsparadoxon Bezugssystem des „Lochs“ Stab kann passieren. Bezugssystem des „Stabs“ Stab kann nicht passieren. Maßstabsparadoxon Addition von beliebigen Geschwindigkeiten: Winkel zw. -Achse und Maßstabsparadoxon Bezugssystem des „Lochs“ Stab kann passieren. Bezugssystem des „Stabs“ Stab kann nicht passieren. Paradoxa Paradoxa kommen (fast immer) zustande durch: • Fehlerhafte Behandlung der Gleichzeitigkeit • Instantane Signalübertragung (keine starren Körper) • Vergessen von Eigenschaften der LorentzTransformationen • Gleichberechtigung von beschleunigten und gleichförmig bewegten Bezugssystemen Das Wichtige auf einer Folie Zusammenfassung Lokales Koordinatensystem Rindler-Koordinaten „Euklidische Koordinaten“ Fermi-Walker Transport: Paradoxa kommen (fast immer) zustande durch: • • • • Fehlerhafte Behandlung der Gleichzeitigkeit Instantane Signalübertragung (keine starren Körper) Vergessen von Eigenschaften der Lorentz-Transformationen Gleichberechtigung von beschl. und gleichf. bewegten Bezugssystemen Quellen [1] C.W. Misner, K.S. Thorne, J.A. Wheeler; Gravitation, Freeman and Company, New York, pp. 163-176, 1973. [2] R. Oloff; Geometrie der Raumzeit (5.Auflage), Vieweg+Teubner Verlag, Wiesbaden, 2010. [3] U.E. Schröder; Spezielle Relativitätstheorie, Harri Deutsch, Frankfurt am Main, pp. 43-54, 1994. [4] H. Günther; Spezielle Relativitätstheorie, Teubner, Wiesbaden, pp. 116-124, 2007. [5] W. Rindler; Essential Relativity, Springer-Verlag, Berlin, pp. 28-51, 1977. [6] C. Ewerz; Klassische Elektrodynamik (Vorlesungsnotizen), http://www.thphys.uniheidelberg.de/~ewerz/scriptum/script_ed_ce.pdf, pp. 95-112, 2015.