CES Mechanik II – Dynamik Übung 9

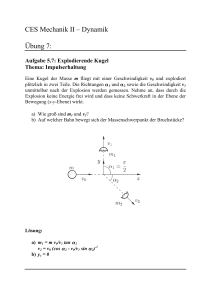
CES Mechanik II – Dynamik
Übung 9:
Aufgabe 5.11: Block auf Rampe
Thema: Energie- und Impulserhaltung für Systeme
Der 12 kg schwere Block A wird aus der Ruhelage von einer 0.4 m hohen Rampe B,
mit einer Masse von 2 kg, losgelassen. Die Rampe kann reibungsfrei auf dem Boden
gleiten.
Bestimme die Geschwindigkeiten des Blockes und der Rampe, wenn der Block das
Ende der Rampe erreicht hat.
Lösung:
vA2 = 2.41 m/s
vB2 = 3.48 m/s
Aufgabe 5.12: Aufprall auf Schräge
Thema: Teilelastischer Stoß
Wie im unteren Bild gezeigt, wird ein Ball der Masse von 0.2 kg auf eine schiefe
Ebene fallen gelassen. Die Stoßzahl beträgt e = 0.8. Desweiteren sei v1 = 10 m/s und
θ = 30°. Reibung kann vernachlässigt werden.
Bestimme die Geschwindigkeit nach dem Aufprall und den Winkel α, sowie die
Energie, welche während des Stoßvorganges verloren geht.
Lösung:
v2 = 8.544 m/s
α = 54.18°
Engerieverlust: 27%
Aufgabe 5.5: Rotierende Kugeln
Thema: Momentensatz
Das im unteren Bild gezeigte System besteht aus zwei Bällen der Masse m, die auf
einem Stab reibungsfrei rutschen können. Die Masse des Rahmens ABO kann
vernachlässigt werden. Der Rahmen ist so gelagert, dass er sich um die z-Achse
drehen kann. Zu Beginn rotiert der Rahmen mit einer Winkelgeschwindigkeit ω 1,
während zwei Seile die Bälle auf einer Kreisbahn mit Radius R1 halten.
Dann werden die Seile gleichzeitig durchgeschnitten, so dass die Bälle bis zu den
Stoppern A und B rutschen, welche sich im Abstand R2 zur z-Achse befinden. Nehme
an, dass die Bälle nicht von den Stoppern abprallen.
a) Bestimme die Winkelgeschwindigkeit ω 2.
b) Welches Moment MO ist erforderlich um das System in der Zeit t0 zu stoppen.
MO sei konstant.
Lösung:
ω 2 = (R1 / R2)2 ω 1
Mo = -(2 m R12 ω 1 ) / t0