Probeklausur zur Vorlesung E1: Mechanik (9

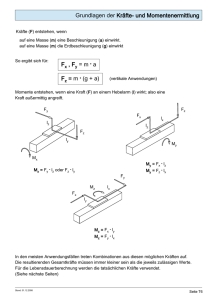
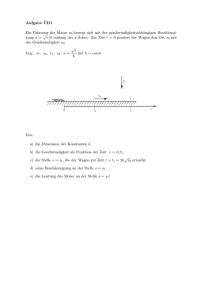
Fakultät für Physik der LMU
28.12.2012
Probeklausur zur Vorlesung E1: Mechanik (9 ECTS)
Wintersemester 2012/2013
Prof. Dr. Joachim O. Rädler
Bitte beachten Sie folgende Informationen:
• Die Bearbeitungszeit beträgt 120 Minuten
• Erlaubte Hilfsmittel: - Taschenrechner
Maximale Punktzahl : 81 P
Aufgabe 1: Flugbahn (8P)
Ein Puck der Masse m soll reibungsfrei über eine Rampe mit Neigungswinkel α und einer Endhöhe
h in einen Korb geschlagen werden, der sich im Abstand d zum Ende der Rampe und in gleicher
Höhe h wie das Ende der Rampe befindet. Die Erdbeschleunigung sei g.
h
α
d
a) Mit welcher Geschwindigkeit v0 muss der Puck die Rampe verlassen, damit er den Korb trifft ?
b) Mit welcher Geschwindigkeit muss der Eishockeyschläger (Masse M) auf den ruhenden und als
elastisch angenommenen Puck stoßen, damit dieser die Geschwindigkeit v0 am Ende der Rampe
erhält? (Nehmen Sie zur Vereinfachung an, dass der Schläger viel schwerer als der Puck ist, also
M>>m)
Aufgabe 2: Rutschbahn (16P)
Ein kleiner Schneeball der Masse m (Punktmasse) befindet sich auf einem halbkugelförmigen
Eisiglu (Radius R). Zum Zeitpunkt t = 0, zu dem die Verbindungslinie Schneeball-Iglumittelpunkt
mit der Vertikalen einen Winkel ϕ0 einschließt, wird der Schneeball losgelassen. Er gleitet
reibungsfrei am Iglu ab. (Die Erdbeschleunigung sei g.)
R
a) Berechnen Sie die Geschwindigkeit v des Schneeballs in Abhängigkeit des Winkels ϕ zur
Vertikalen.
b) Unter welchem Winkel hebt der Schneeball von der Igluoberfläche ab ?
c) Mit welcher Geschwindigkeit bewegt sich der Schneeball zu diesem Zeitpunkt und
in welcher Höhe über dem Boden befindet er sich?
d) Wenn der Schneeball über den Iglu rollen würde, wäre dann die Höhe bei der sich der Schneeball
abhebt, gleich hoch, höher oder tiefer gelegen? (kurze Begründung)
Aufgabe 3: Balken (12P)
Ein Ende eines homogenen Balkens (Länge L = 10m, Masse M =
100kg) sei über ein Scharnier drehbar an einer vertikalen Wand
befestigt. Ein Drahtseil halte den Balknen in horizontaler
Position, wobei das Drahtseil 6m von der Wand entfernt mit dem
Balken verbunden sei. Am freien Ende des Balkens wird ein
Körper der Masse 400kg angehängt.
a) Wie groß ist die Zugkraft im Seil?
b) Wie groß ist die horizontale Kraft im Scharnier?
c) Wie groß ist am Scharnier die vertikale Kraft auf den Balken?
Betrachten Sie nun ein Drahtseil variabler Länge, das in der Höhe 8m über dem Balken in der Wand
befestigt ist.
d) In welcher Entfernung von der Wand muss es am Balken angebracht werden, damit die Kraft auf
das Scharnier keine vertikale Komponente hat?
Aufgabe 4: Physikalisches Pendel (20P)
Ein Uhrenpendel bestehe aus zwei masselosen Stangen der Länge L=1m und einer Scheibe mit
Radius r=10cm und Masse m=0.5kg (siehe Zeichnung).
a) Bestimmen Sie das Drehmoment M(Ф), welches durch die Erdbeschleunigung (g=9.81m/s2)
auf das Pendel ausgeübt wird, und entwickeln Sie es um die Ruhelage nach Taylor bis zur
ersten Ordnung in Ф.
b) Stellen Sie in Näherung eine lineare Bewegungsgleichung für den zeitabhängigen Winkel
Ф(t) auf.
c) Zeigen Sie durch explizite Integralrechnung, dass das Trägheitsmoment der homogenen
1 2
Kreisscheibe I Scheibe = mr ist.
2
d) Berechnen Sie die Schwingungsdauer des Pendels für den Fall einer starr mit den Stangen
verbundenen Scheibe.
e) Um wie viel Prozent ändert sich die Schwingungsdauer, wenn die Scheibe frei um ihre
Aufhängsachse rotieren kann?
Aufgabe 5: Gravitation (16P)
Stellen Sie sich vor, Sie bohren zentral durch die ganze Erde ein Loch und lassen einen Stein der
Masse m in dieses Loch fallen.
a) Wie hängt die Gravitationskraft FG(r) vom Abstand r zum Erdmittelpunkt ab?
Nehmen Sie dabei an, dass die Erde eine Kugel mit homogener Dichte und Radius R = 6400km sei.
(Hinweis: Beachten Sie, dass FG(r) auf der Erdoberfläche der bekannten Schwerkraft entsprechen
muss)
b) Wo erreicht der Stein die maximale Geschwindigkeit und wie groß ist diese?
c) Wie lange braucht der Stein, bis er auf der anderen Seite des Tunnels ankommt?
Aufgabe 6 Verständnisfragen (9P)
a) Zeigen sie, dass sich der Drehimpuls eines Massepunktes unter dem Einfluß eines
Zentralkraftfeldes nicht ändert.
b) Wie ist in der Elastizitätstheorie die “Querkontraktionsverhältnis (Poisson-Zahl)” definiert ?
c) Was versteht man unter einer “freien Achse” eines starren Körpers ?