Kinematik
Werbung
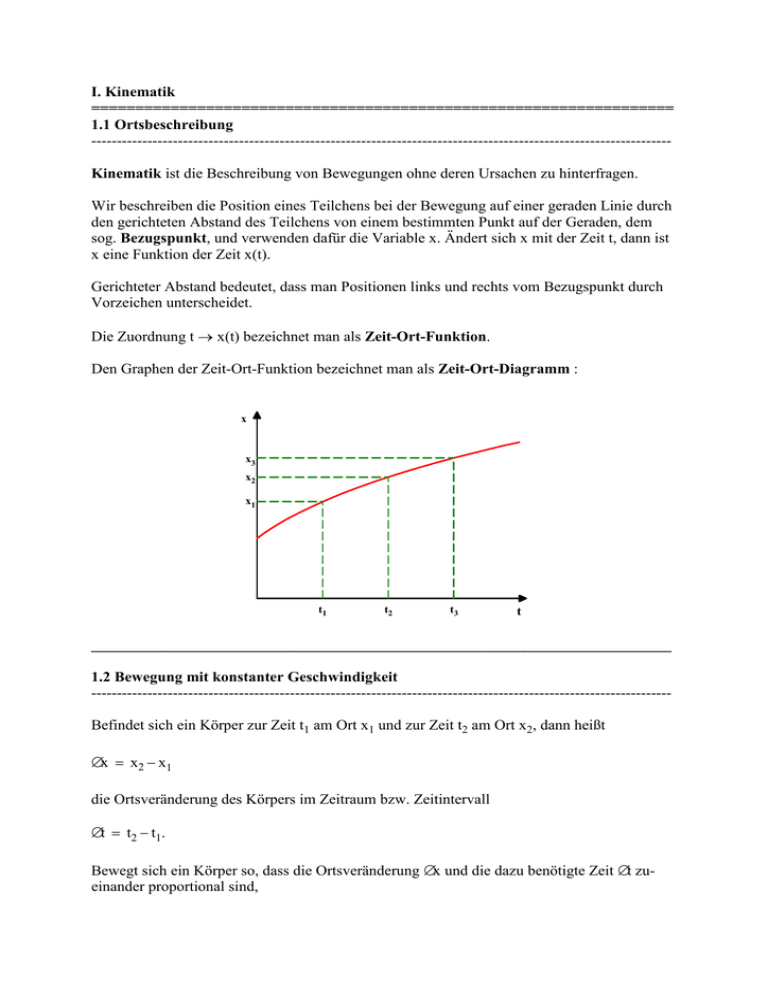
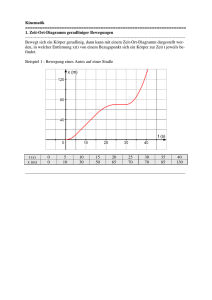
I. Kinematik ================================================================== 1.1 Ortsbeschreibung -----------------------------------------------------------------------------------------------------------------Kinematik ist die Beschreibung von Bewegungen ohne deren Ursachen zu hinterfragen. Wir beschreiben die Position eines Teilchens bei der Bewegung auf einer geraden Linie durch den gerichteten Abstand des Teilchens von einem bestimmten Punkt auf der Geraden, dem sog. Bezugspunkt, und verwenden dafür die Variable x. Ändert sich x mit der Zeit t, dann ist x eine Funktion der Zeit x(t). Gerichteter Abstand bedeutet, dass man Positionen links und rechts vom Bezugspunkt durch Vorzeichen unterscheidet. Die Zuordnung t → x(t) bezeichnet man als Zeit-Ort-Funktion. Den Graphen der Zeit-Ort-Funktion bezeichnet man als Zeit-Ort-Diagramm : x x3 x2 x1 t1 t2 t3 t ___________________________________________________________________________ 1.2 Bewegung mit konstanter Geschwindigkeit -----------------------------------------------------------------------------------------------------------------Befindet sich ein Körper zur Zeit t1 am Ort x1 und zur Zeit t2 am Ort x2, dann heißt ∆x = x2 − x1 die Ortsveränderung des Körpers im Zeitraum bzw. Zeitintervall ∆t = t2 − t1. Bewegt sich ein Körper so, dass die Ortsveränderung ∆x und die dazu benötigte Zeit ∆t zueinander proportional sind, ∆x ∼ ∆t dann spricht man von einer gleichförmigen Bewegung. Die Proportionalitätskonstante v = m ∆x mit v = 1 s ∆t gibt die Größe der Ortveränderung pro Sekunde bzw. pro Zeiteinheit an und heißt Geschwindigkeit v (engl velocity) der Bewegung. Beachte : v > 0 : Die Bewegung erfolgt in positive x-Richtung v = 0 : Der Körper ruht v < 0 : Die Bewegung erfolgt in negative x-Richtung. Bemerkung : Bewegt sich der Körper im Zeitintervall t1 ; t2 nicht mit konstanter Geschwindigkeit, dann ∆x heßt der die mittlere Geschwindigkeit oder Durchschnittsgeschwindigkeit v in diesem ∆t Zeitintervall. Das Zeit-Ort-Diagramm : x x x2 ∆x = x2 − x1 x2 x1 ∆x = x2 − x1 x1 ∆t = t2 − t1 t1 ∆t = t2 − t1 x0 t2 t t1 Es gilt : Es gilt : x(t) = v⋅⋅t x(t) = x0 + v⋅⋅t t2 t ___________________________________________________________________________ 1.3 Das Zeit - Geschwindigkeits - Diagramm -----------------------------------------------------------------------------------------------------------------v v0 ∆t t1 t2 t Wegen ∆x = v0⋅∆t ist die Fläche unter tem t-v-Diagramm ein Maß für den zurückgelegten Weg. ___________________________________________________________________________ 1.4 Die Momentangeschwindigkeit ------------------------------------------------------------------------------------------------------------------ x1 ∆x = x1 − x x ∆t = t1 − t t t1 Befindet sich der Körper zur Zeit t am Ort x und zur Zeit t1 am Ort x1, dann ist die mittlere Geschwindigkeit im Zeitintervall t ; t1 gegeben durch v(t ; t1) = x1 − x t1 − t Den Grenzwert v(t) = lim v(t ; t1) = lim t1 → t t1 → t x1 − x t1 − t bezeichnet man als Momentangeschwindigkeit v(t) des Körpers zur Zeit t. Mathematisch gesehen ist die Momentangeschwindigkeit zur Zeit der Anstieg der Tangente an den Graphen Zeigt-Ortsfunktion im Punkt t; x(t). Eine Bewegung, bei der sich die Momentangeschwindigkeit ändert, heißt beschleunigte Bewegung. ___________________________________________________________________________ 1.5 Die Beschleunigung -----------------------------------------------------------------------------------------------------------------Hat ein Körper zur Zeit t1 die Momentangeschwindigkeit v1 und zur Zeit t2 die Momentangeschwindigkeit v2, dann heißt ∆v = v2 − v1 die Geschwindigkeitsänderung des Körpers im Beschleunigungszeitraum ∆t = t2 − t1. v v2 ∆v = v2 − v1 v1 ∆t = t2 − t1 t1 t2 t Bewegt sich ein Körper so, dass die Geschwindigkeitsänderung ∆v und der Beschleunigungszeitraum ∆t zueinander proportional sind, ∆v ∼ ∆t dann spricht man von einer gleichförmig beschleunigten Bewegung. Die Proportionalitätskonstante a = ∆v m mit a = 1 2 ∆t s gibt die Größe der Geschwindigkeitsänderung pro Sekunde bzw. pro Zeiteinheit an und heißt Beschleunigung a (engl. acceleration) der Bewegung. Beachte : a > 0 : Die Geschwindigkeit wird erhöht a = 0 : Der Körper bewegt sich mit konstanter Geschwindigkeit a < 0 : Die Geschwindigkeit wird erniedrigt Das Zeit-Geschwindigkeit-Diagramm : v v v0 t t Es gilt : Es gilt : v(t) = a⋅⋅t v(t) = v0 + v⋅⋅t ___________________________________________________________________________ 2.3 Die Zeit - Ort - Funktion ------------------------------------------------------------------------------------------------------------------ v = v0 + a⋅⋅t v = a⋅⋅t v0 t Es gilt : x(t) = Es gilt : 1 1 1 t ⋅ v = t⋅ a⋅t = a⋅t2 2 2 2 x(t) = 1 2 a⋅t + v0t 2 Hat ein Körper zu Zeit t = 0 die Momentangeschwindigkeit v0 und die Ortkoordinate x0 und bewegt er sich mit der konstanten Beschleunigung a weiter, dann ist seine Ortskoordinate x(t) zur Zeit t gegeben durch x(t) = a 2 ⋅ t + v0 ⋅ t + x0 2 Das Zeit - Ortsdiagramm : Das Zeit- Ortdiagramm ist einer Bewegung mit konstanter Beschleunigung ist eine Parabel. Beispiel : m aus der Ruhe heraus vom Bezugspunkt weg. s2 Zeichne das Zeit - Ort - Diagramm der Bewegung. Ein Körper bewegt sich mit a = 0,20 ___________________________________________________________________________ 2.4. Die Ort - Geschwindigkeits - Funktion -----------------------------------------------------------------------------------------------------------------Hat ein Körper zur Zeit t = 0 die Geschwindigkeit v0 und bewegt er sich mit konstanter Beschleunigung a vom Bezugspunkt weg, dann gilt gilt für die Orskoordinate x und die Geschwindigkeit v zur Zeit t (1) v = v0 + a⋅t ⇔ (2) x = t = v − v0 a 1 2 at + v0t 2 Einsetzen von (1) in (2) : 2 v − v0 1 v − v0 v2 − v0 2 1 v − v0 x = a + v0 = (v − v ) + v ⇔ v2 − v02 = 2ax = 0 0 2 a a a 2 2a Hat ein Körper zur Zeit t = 0 die Geschwindigkeit v0 und bewegt er sich mit konstanter Beschleunigung a weg, dann gilt gilt für seine Geschwindigkeit v(x) am Ort x v(x)2 − v02 = 2ax __________________________________________________________________________