Ms M(T) T T T T - FU Berlin
Werbung
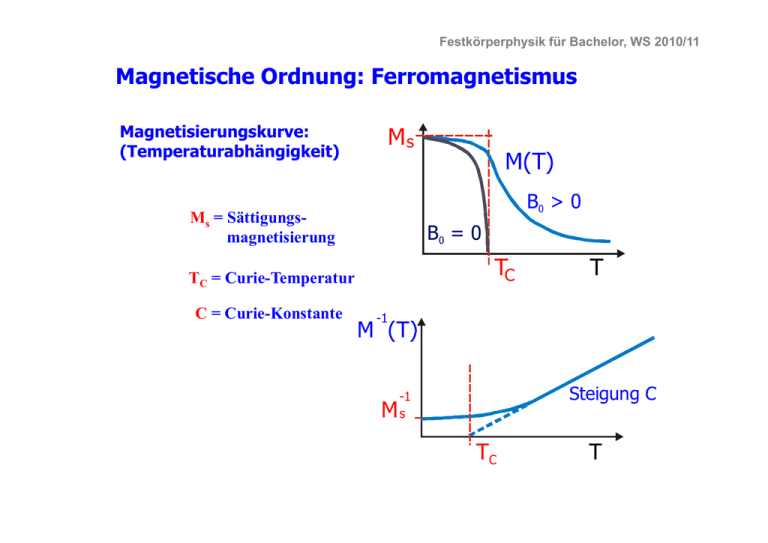
Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung: g Ferromagnetismus g Magnetisierungskurve: (Tempe at abhängigkeit) (Temperaturabhängigkeit) Ms B0 > 0 Ms = Sättigungsmagnetisierung B0 = 0 TC TC = Curie-Temperatur C = Curie-Konstante M(T) T -1 M (T) M Steigung C -1 1 s TC T Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung: g Antiferromagnetismus g Ordnungsarten: Beispiele: (Quelle: Ashcroft, Mermin, Solid State Physics, Saunders, Philadelphia) Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung: g Antiferromagnetismus g Magnetisierungskurve: (Tempe at abhängigkeit) (Temperaturabhängigkeit) M(T) TN = Néel-Temperatur TN D = Debye-Temperatur T -1 1 M (T) 3 D 3 TN T Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung g magnetische Suszeptibilität (Quelle: Ch. Kittel, Introduction to Solid State Physics, Wiley, New York) Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung g magnetische Suszeptibilität vom Antiferromagnet MnF2 (Quelle: Ch. Kittel, Introduction to Solid State Physics, Wiley, New York) Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung: g Ferrimagnetismus g Spinell-Struktur: A2+B23+O4 (kubische Ferrite) Beispiel: p Magnetit Fe3O4 Fe3+(Fe3+Fe2+) O4 Fe3+: S = 5/2; 5 µB Fe2+: S = 2; 4 µB (Quelle: Ch. Kittel, Introduction to Solid State Physics, Wiley, New York) A2+-Ionen sitzen auff 8 tetraedrischen Gitterplätzen, p , B3+-Ionen sitzen auf 16 oktaedrischen Gitterplätzen alle Austauschwechselwirkungen sind antiferromagnetisch: zwischen den A2+-Ionen, Ionen zwischen den B3+-Ionen Ionen und zwischen A2+ und B3+-Ionen Ionen Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung: g Ferrimagnetismus g Ordnungsarten: Beispiele: Festkörperphysik für Bachelor, WS 2010/11 Magnetische g Ordnung: g Ferrimagnetismus g Magnetisierungskurve: (Tempe at abhängigkeit) (Temperaturabhängigkeit) Ms M(T) Ms = Sättigungsmagnetisierung Tkomp TC T MA TC = Curie-Temperatur Tkomp = Kompensationstemperatur Ms M(T) Tkomp MB TC bei T = Tkompp heben sich die magnetischen Momente der beiden Untergitter exakt auf 8 magnetisch sehr stabil bei T = Tkomp T