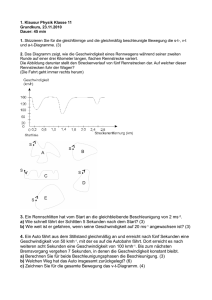
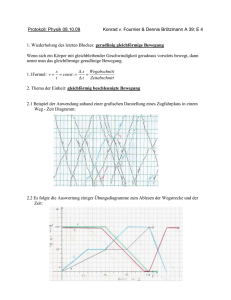
1 MECHANIK --- BEWEGUNGEN Bewegung heißt, daß sich die

MECHANIK --- BEWEGUNGEN
Bewegung heißt, daß sich die Lage eines betrachteten Objektes ändert.
Dazu muß die Lage angegeben werden, am besten durch Koordinaten,
z.B. geographische Länge und Breite.
In der Physik meist: Kartesische Koordinaten:
Punkt P wird festgelegt
durch seine Koordinaten
(x,y,z).
P
z
z
x
y
y
x
Angabe von P durch den Ortsvektor
P
z
Koordinaten sind die
Längen der Strecken, in
die in die x,y,z
Richtung gegangen
werden muss, um zu P
zu gelangen.
Der Ortsvektor hat stets seinen
Beginn im Koordinatenursprung.
z
x
y
y
x
Bei BEWEGUNGEN ist der ORTSVEKTOR eine FUNKTION
der ZEIT d.h.
1
Wir betrachten zunächste Bewegung eines Punktes.
Allgemeinster Fall: Bewegung entlang einer Kurve im Raum, z.B.
fliegender Vogel.
Momentane Lage durch Ortsvektor gegeben
Abb 2.1 Biologiische Physik
ist Lageänderung zwischen
1s und 2s
ungefähr der zurückgelegter Weg
SPEZIALFALL GLEICHFÖRMIGE BEWEGUNG:
in gleichen Zeiten gleiche Wege
Weg in 1. Sekunde
Weg in 2. Sekunde
Weg in 3. Sekunde
Weg in 4. Sekunde
Gleichförmige Bewegung ist immer
GERADLINIGE BEWEGUNG
2
Definition der GESCHWINDIGKEIT
Kohärente Einheit: Einheit die aus den Grundeinheiten nur
durch Multiplikation und Division erhalten wurde
[v] = m.s-1
andere Einheiten km/h mph mm/d
Empfehlung: rechnen Sie immer mit kohärenten Einheiten!!
1 m/s = ??? km/h
3
Falls die Bewegung in eine Richtung erfolgt:
ist die Richtung ohnehin klar
Es genügt, die Entfernung von einen willkürlichen gewählten
Punkt anzugeben
WEGZEIT DIAGRAMM zur VERANSCHAULICHUNG VON
BEWEGUNGEN
WEGZEIT DIAGRAMM verwendet ein Koordinatensystem wobei
•in der xRichtung die Zeit aufgetragen wird (Zeitachse, t-Achse)
• in der y Richtung der Weg (Wegachse, s-Achse)
Auf der t-Achse wird die Zeit ab einen willkürlich gewählten
Anfangspunkt für die Zeitmessung aufgetragen
(zB Abfahrtszeitpunkt des Zuges)
Auf der s-Achse wird der Weg ab einen willkürlich gewählten
Anfangspunkt für die Längenmessung aufgetragen.
Bei ausgedehntenen Körpern eines markanten Punktes
zB Entfernung des Puffers des letzen Waggons vom
Prellbock des Abfahrtsbahnhofes
Anfangspunkte werden üblicherweise günstig gewählt
Bewegung ist
üblicherweise
durch eine
Kurve im
(s,t)-Diagramm
dargestellt:
s = s(t)
s
s(t)
t
4
Spezialfall: Bewegung im Weg-Zeit Diagramm wird durch
eine Gerade dargestellt
s
In gleichen Zeiten
werden gleiche
Wege
zurückgelegt:
∆s
--->
∆s
t
∆t
gleichförmige
Bewegung
∆t
Geschwindigkeit ist die Steigung der Geraden:
Steil: große Geschwindigkeit
flach: geringe Geschwindigkeit
Horizontal ???
negative Steigung ??
5
GERADLINIGE UNGLEICHFÖRMIGE BEWEGUNG
Die Definition der Geschwindigkeit
Kann nicht mehr verwendet werden da nicht mehr in
gleichen Zeiten gleiche Wege zurückgelegt werden
Wir führen die Mittlere Geschwindigkeit ein
Das ist jene Geschwindigkeit mit der eine
gleichförmige Translation erfolgen müßte,
um in der Zeit ∆t den Weg ∆s zurückzulegen
04.09.2005
Hängt von der Wahl von ∆t ab !!!!!
Leicht zu sehen am Beispiel des freien Falls:
Beim freien Fall ist s = (g/2) . t2
mit g = 10 m.s-2
Daher s = 5 m.s-2(g/2) . t2
Z.B. für t = 2s ergibt sich
s= 5 m.s-2.(4s) 2=20m.s-2.s2=20m
Einige Werte:
Zeit
0
1
2
3
Weg
0
5
20 45
4
5
1,001
1,01
80 125 5,010005 5,1005
1,1 s 1,5
6,05 11,25 m
6
Geschwindigkeit zwischen der 1. und 2. Sekunde:
∆t = 2s –1s = 1s,
∆s = 20m – 5m = 15 m,
v = 15m / 1s = 15 m s-1
Geschwindigkeit zwischen der 1 und 1,5 Sekunden:
∆t = 1,5s –1s = 0,5s,
∆s = 11,25m – 5m = 6,25 m,
v = 6,25m / 0,5s = 12,5 m s-1
Geschwindigkeit ist vom Zeitintervall abhängig!!!!
Momentangeschwindigkeit: Geschwindigkeit in einem
kurzen Moment ∆t
Was ist kurz????
∆t---->0
Vermutung!!!
7
Mittlere Geschwindigkeit:
Momentangeschwindigkeit:
Momentangeschwindigkeit ist erster Differentialquotient
des Weges nach der Zeit
Anschaulich Momentangeschwindigkeit ist die Steigung der
Tangente an die Kurve im WegZeit Diagramm
s
Steigung der
Geraden ist
die mittlere
Geschwindigkeit
zwischen den
Zeitpunkten
t1 und t2
s2
s2-s1
s1
t2-t1
t1
t
t2
8
s
Kürzeres Zeitintervall
andere Sekante
(Gerade), andere
Steigung
t
s
Noch kürzeres
Zeitintervall:
Wieder andere
Steigung
t
9
s
Noch kürzeres
Intervall: Sehne
kaum von der
Kurve
unterscheidbar
t
s
Zeitintervall
----> 0
Sehne geht über in
die Tangente
t
Steigung der Tangente ist die Momentangeschwindigkeit
10
Falls Weg als Funktion der Zeit gegeben ist Geschwindikeit
durch Differenzieren ermittelbar
BESCHLEUNIGUNG:
wie rasch sich die Geschwindigkeit ändert
Die Beschleunigung ist wie die Geschwindigkeit ein Vektor
GEICHMÄSSIG BESCHLEUNIGTE BEWEGUNG:
in gleiche Zeiten gleiche GESCHWINDIGKEITSZUNAHME
Der freier FALL ist ein BEISPIEL für eine GEICHMÄSSIG
BESCHLEUNIGTE BEWEGUNG.
für jedes ∆t dieselbe BESCHLEUNIGUNG
(Geschwindigkeitsänderung)
11
UNGLEICHMÄSSIG BESCHLEUNIGTE BEWEGUNGEN
Überlegungen analog zur Geschwindigkeit
Momentanbeschleunigung
Der Beschleunigungsvektor muß nicht
in Richtung der Bewegung zeigen !!!!
1.10.04
Falls es sich um eine geradlinige Bewegung handelt:
Geschwindigkeits-Zeit Diagramm
v
v(t)
t
Die Beschleunigung
ist anschaulich die
Steigung der
Tangente:
Positiv wenn die
Geschwindigkeit
zunimmt,
negativ bei Abnahme
12
Eine gleichförmige Bewegung a=0 ergibt eine
horizontale Linie im (v,t) Diagramm
v
v(t)
Die Fläche unter der
Geschwindigkeits-Zeit Kurve
ist der zurückgelegter Weg
v
t
∆t
v
Betrachte kurzes
Zeitintervall ∆t, in
diesem verändert sich die
Geschwindigkeit kaum.
v(t)
∆s
Daher ist ∆s = v(t). ∆t.
t
∆t
Das ist die schmale Fläche
unter der Kurve
13
Nun hintereinaderliegende kurze Zeitintervalle
v
Fläche jedes
Streifens ist der
zurückgelegte Weg.
v(t)
t
Summe aller
Streifen ist die
Fläche unter der
Kurve
Analog für Beschleunigung: v= Fläche unter der Kurve
im Beschleunigungs-Zeit Diagramm
14
Zusammenfassung:
Umkehrungen:
15
Beispiel für die Anwendung dieser Integrale:
Gleichmäßig bescheunigte Bewegung, a = const
= ???
= ???
Bedeutung von v0 und s0 Anfagsgeschwindigkeit und Lage
Freier Fall: durch spezielle Wahl des Koordinatensystems
läßt sich eine einfache Formel finden:
Zum Zeitpunkt des Loslassens ist s0=0.
Entfernungen werden normal auf die Erdoberfläche
(nach unten ist positiv) gemessen.
Im Augenblick des Loslassens ist v0=0
s0=0, v0=0, a=g=10 m s-2
16
Wurf nach oben: andere Koordinatensystem:
Entfernung vom Erdboden nach oben positiv, daher a = - g
v0 ist positiv.
s=(– g/2)t2+v0.t
v=v0 – g.t
Am Umkehrpunkt (höchster Punkt) ist v = 0 dies
geschieht zur Zeit th, das Objekt befindet sich dann sh
über dem Boden.
0=v0 – g.th
--> th=v0/g
sh =(– g/2) (th )2+v0. th
Eingesetzt ergibt sich: sh=v02/(2g)
ZUSAMMENSETZUNG VON BEWEGUNGEN:
Falls sie voneinander unabhängig sind, ergeben sich
Wege, Geschwindigkeiten und Beschleunigungen durch
VEKTORIELLE ADDITION
v1 + v2
v2
v1
Vogel fliegt bei Wind mit 3m/s aus NW mit 12 m/s nach N.
Selbstvertändlich wird er vom Wind abgetrieben.Welche
Geschwindigkeit und Richtung hat er über Boden?
17
N
Wind
Vogel
5m/s
45°
12m/s
v
φ
Bewegung über Boden
Cosinussatz:
v2=(12m/s)2+(5m/s)2-12m/s.5m/s.cos 45°
v=10,1m/s
Sinussatz:
sin φ:5m/s=sin 45°:v
--> sin φ =5m/s.sin45°/10,1m/s
Vogel fliegt N12,1°O
φ=12,1°
Schräger Wurf nach oben: Kann als Zusammensetzung
aus freiem Fall und gleichförmiger Bewegung aufgefaßt
werden. Geschwindigkeiten wund Wege werden mit vh
und vv bzw sh und sv bezeichnet
Koordinatensystem: v-Richtung vertikal nach oben
h-Richtung horizontal
Erdboden hat x=0
Anfangsgeschwindigkeit hat v0v in v-Richtung
v0h in h Richtung
Erdbeschleunigung in die negative v-Richtung
18
Von früher:
Vertikal: v0 = v0v, a=-g
vv=-g.t+ v0v
sv=(-g/2).t2+v0v.t
horizontal: v0 = v0h, a=0
vv=v0h
sv=v0h.t
Beispiel: Lama spuckt mit 10 m/s aus der Schnauze, die 1m
über Boden ist unter 45 ° nach oben. Wie weit müssen die
Zoobesucher entfernt stehen um nicht getroffen zu werden.
19
Koordinatensystem: Vertikalentfernung vom Erdboden nach oben
positiv gemessen.
v0v=10m/s.sin 45° = 7,07m/s
45°
v0h=10m/s.sin 45° = 7,07m/s
s0v=1m (da über Boden)
s0h=0
a= -10ms-2 in die Vertikalrichtung
Allgemein ist: s=(a/2).t2+v0.t+s0
Eingesetzt horizontal: sh=(7,07m/s).t (*)
Eingesetzt vertikal: sv=(-5m/s2).t2+(7,07m/s).t+1m
Wenn Speichel am Boden auftrifft ist sv=0.
Daher 0 =(-5m/s2).t2+(7,07m/s).t+1m
Daraus t ermittelbar. In (*) eingesetzt ergibt sich de nötige
Sicherheitsabstand.
Beispiel: Sprung aus dem Stand.
Referenzpunkt für unsere Überlegungen ist der Schwerpunkt.
Am Ende der Absprungphase sei er 1m über Boden.
Der Sprung ist dann ein “Wurf” nach
oben auf 1,6 m Höhe (Rekord 1.65m)
20
Koordinatensystem so gewählt
daß der Nullpunkt der Entfernungsmessung 1m über Boden ist.
Daher ist die “Wurfhöhe” h= 0.6m
Aus h=v2/2g ergibt sich die Absprunggeschwindigkeit zu v2=2gh
v2=2 . 10ms-2 . 0,6m
Daher v=3.46 m/s
Absprungphase gleichmäßige Beschleunigung von 0.6 auf
1m über Boden mit der Beschleunigung a.
Wir wählen geeignete Koordinaten: Nullpunkt ist 0,6m über
Boden:
---> (gleichmäßig) beschleunigte Bewegung von 0 auf 0.4 m
Die Endgeschwindigkeit bei der Beschleunigungsphase muß
3.46 m/s sein
Aus s=(a/2) . t2 und v=a .t ergibt sich
a=v2/(2s)=15ms-2
Aus t=v/a ergibt sich die
Beschleunigingszeit zu 0,23 s
Übungsaufgabe: Heuschrecke hüpft 59 cm. Hat eine
Beschleunigungsstrecke von 4cm. Wie groß ist die
Beschleunigung, wie lange dauert der Vorgang?
21
KRAFT und MASSE
Beschleunigung kommt nicht von selbst sondern durch
Muskelkontraktion
Triebwerk
Motor
…...
Allgemeiner, erst durch Wechselwirkung mit einem
anderen Objekt kann eine Beschleunigung auftreten.
Ohne Wechselwirkung findet eine gleichförmige geradlinige
Bewegung (TRÄGHEITSPRINZIP, Newton)
Falls Wechselwirkung zwischen zwei Körpern auftritt
beeinfussen sich die Bewegungen gegenseitig
es tritt eine BESCHLEUNIGUNG auf.
Wir nennen die URSACHE einer BESCHLEUNIGUNG
die KRAFT
= 1 N (Newton)
07.10.2005
Ein frei fallender Körper fuhrt eine gleichmäßig beschleunigte
Bewegung mit g=10 ms-2 aus (experimentelles Faktum),
g ist zum Erdmittelpunkt gerichtet
22
1 N ist die Schwerkraft von 0,1kg kN,
Einheit + SI Vorsilbe: mN, kM, MN
zB auf Kanaldeckel steht “Tragfahigkeit”
150 kN. Welche Masse??
Es gibt zwei Arten von Kräften
KONTAKTKRAFTE: Durch die Wechselwirkung der Moleküle
mit einer Reichweite 10 bis 100 pm
z.B. Kohäsion, Reibung,Verformung
FERNWIRKUNGSKRAFTE Reichweite unbeschränkt aber mit
der Entfernung abnehmend: Graviatation, elektrostatische ,
magnetische Kräfte
Bei WECHSELWIRKUNG Kraft von A auf B ist
entgegengesetzt zu Kraft von B auf A
Abb. 2.11 Biologische Physik
KRAFT ist VEKTOR daher VEKTORIELLE ADDITION
Addition durch Vektorparellelogramm
oder
23
Vektoraddition durch Parallelverschiebung
Einen Vektor so verschieben, daß er bei der
Spitze des anderen Vektors beginnt
Summenvektor geht vom Beginn des
ersten Vektors zum Ende des zweiten
Vektors.
ZERLEGUNG von KRÄFTEN in vorgegebene RICHTUNGEN
durch Projektion auf diese Richtung.
Schiefe Ebene: Zerlegung der Schwerkraft in zwei Kräfte:
•Normal zur Ebene, drückende Kraft (wird durch die Struktur
aufgefangen)
•In Richtung der Ebene, treibende Kraft: Muß aufgewendet
werden, um Gegenstand am hinabrollen, -gleiten zu hindern
Abb. 2.16 Biologische Physik
24
Beispiel: Kraft beim Hochsprung.
Es war a=15ms-2
Mit m= 50 kg ergibt sich F=750N
Dazu noch Schwerkraft
500N
Muskel müssen
1250 N aufbringen
Beispiel. Zerlegung von Kräften bei Aufhängung an Seilen,
Rucksack hat 25 kg
Schwerkraft muß kompensiert werden
Die Kraft kann wegen der Biegsamkeit der Schnüre nur in die
Richtung der Seile wirken
25
Betrachte markiertes Dreieck:
30°
m.g/2
F
sin 30° = m.g/(2F)
F = m.g/(2.sin30°) = 25 kg.10 ms-2/(2.0,5) = 250 N
Bei großer Beschleunigung große Kraft!!
Z.B plötzliches Abbremsen.
Längerer “Bremsweg” bedeutet geringere Beschleunigung:
Dehnbarer Sicherheitsgurt,
Kletterseil,
deformierbare Knautschzone
Abfedern beim Aufsprung
Kurzer “Bremsweg” bedeutet große Beschleunigung:
26
Beispiel: steifer Aufsprung:
Schienbein hält maximal 50000N aus, verkürzt sich dabei um 1 cm.
Aus welcher Höhe ist diese Grenze erreicht (Masse = 75 kg),
beidbeiniger Aufsprung.
a=F/m= 1333ms-2
Auftreffgeschwindigkeit aus v2 = 2.a.s = 2.1333.0,01m2s-2
v=5.16 m/s
Absprunghöhe aus v2 = 2.g.h --> h = v2/2g = 1.33 m
Falls Summe der Kräfte = 0: Ruhe oder gleichförmige Translation
ARBEIT: KRAFT verursacht BEWEGUNG
ARBEIT KRAFT x WEG
W = F . s, skalares Produkt, es kommt auf die Richtung an!!
Hier ist die Arbeit Null!!
F
s
Einheit: [W] = 1N . 1m = 1Nm = 1 J Joule
1 Joule ist jene Arbeit die unter der Wirkung von 1 N bei
einer Verschiebung von 1 m auftritt
27
Weg
Arbeit gegen die Schwerkraft:
HEBEARBEIT W = m . g . h
Da Hebekraft und Weg parallel sind ist
das skalare Produkt nicht nötig.
Kraft um Masse
zu heben
Masse
Schwerkraft
m.g
Kraft-Weg Diagramm
F
Arbeit (m.g.∆s) ist die Fläche
unterhalb der Kurve im
Kraft - Weg Diagramm
m.g
s
∆s
Beispiel: Rollstuhl 80 kg im Lift ein Stockwerk (3m) gefahren
W = m.g.h=80 kg. 10 ms-2.3 m= 2400 Nm= 2400 J
Auf einer Rampe mit 15° Neigung??
s
3m
15°
m.g
Es ist s = 3m /sin 15° = 11,59 m
Winkel zwischen Kraft und Weg ist 90° + 15° = 105°
Arbeit = 11,59 m . 800 N . cos 105° = -2400 N
28
s
3m
15°
m.g
Anderer Weg:
Treibende Kraft = m . g. sin 15°
Arbeit = F . S = m .g. sin15° . 3 m /sin 15° = m.g.3m=2400 J
BESCHLEUNIGEN EINER MASSE
F = m . a, s = a/2 . t2
W = ½ma 2t2= ½.m.v2
Aufgewendete Arbeit ist in der bewegenden Masse gespeichert
2
LEISTUNG ARBEIT pro ZEIT
5.10.04
Einheit [P] = J.s-1 = W
29
Isoliertes System: Ein Bereich der gegen die Außenwelt abgegrenzt
ist und mit dieser nicht in Wechselwirkung steht.
Kein (merklicher) Austausch an Energie und Masse.
(auch abgeschlossenes System genannt)
Erhaltungssätze der Mechanik:
In isolierten System ist Summe der Massen konstant,
Summe der Energien
“Energieverlust” zB bei Reibung ist
Umwandlung in eine andere Form (Wärmeenergie)
30