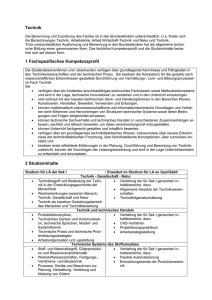
DC-Servomotor mit Tachogenerator im Regelkreis

DC-Servomotor mit Tachogenerator
DC-Servomotor mit Tachogenerator im Regelkreis
Gegeben: DC-Servomotor mit Tachogenerator im Regelkreis
Tacho
filter
circuit
Leistungsverstärker
vu = 2
+
-
UX(s)
-
+
UU(s)
C1b
100 kΩ
100 kΩ
R2
100 kΩ
C1a
-Uref
100 kΩ
-
RW
R1a
R1b
-
+
+
-UW(s)
-UE(s) = -UW(s) + UX(s)
Auszug aus dem Datenblatt des Motors mit Tachogenerator:
No load speed @ 24 V dc:
2300 rpm
Mechanical time constant (T1):
20 ms
Terminal Resistance (Ri):
7,8 Ω
Rotor inductance (LA):
5,0 mH
Tachogenerator voltage constant (ktg): 3,25 mV/rpm
Tacho filter circuit (low pass filter): G(s) = 1/(1 + 2·10-3Sek.·s)
Gesucht: 1) Geben Sie die Übertragungsfunktion Fs(s) in der Streckendarstellung an.
Eingangsgröße: Eingangsspannung in den Leistungsverstärker
Ausgangsgröße: Spannung nach Tachofilter
Hinweis: Dieser Kleinmotor kann als stark gedämpftes PT2-Element mit der
mechanischen Zeitkonstante als T1 und der Ankerzeitkonstante als T2
aufgefasst werden. Mit dem Tachofilter wird die Strecke zum PT3.
2) Berechnen Sie die Übertragungsfunktion FR(s) eines betragsoptimalen PIReglers.
motortacho_rk_2.doc
Seite 1/4
Vanek 2006.04.08
DC-Servomotor mit Tachogenerator
3) Dimensionieren Sie R1 und C1. Verwenden Sie Bauteile der Reihe E12
(10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82, 100, ...).
Stellen Sie R1 und C1 durch Serien- bzw. Parallelschaltungen dar.
4) Geben Sie die tatsächliche Übertragungsfunktion FR(s) des Reglers mit den

von Ihnen gewählten Bauteilen in der Form FR ( s ) = k R 1 +
1
sTN

 an.


5) Bestimmen Sie den zeitlichen Verlauf der Spannung uX(t) bei einer
sprunghaften Änderung von uW(t) (Sprungantwort). Verwenden Sie dazu ein
Simulationsprogramm Ihrer Wahl.
6) Welchen Wert müssen Sie bei der Führungsgröße UW einstellen, um eine
Drehzahl von 1000 U/min zu erhalten?
motortacho_rk_2.doc
Seite 2/4
Vanek 2006.04.08
DC-Servomotor mit Tachogenerator
Lösung:
1) Übertragungsfunktion Fs(s):
k = Ua / Ue = vu · (2300 min-1 · 3,25 mV/min-1) / 24 V = 2 · 7,48V / 24 V = 0,622
T1 = 0,02 Sek. (Mechanische Zeitkonstante)
T2 = 2⋅10-3 Sek. (Tachofilter)
T3 = LA / Ri = 5,0⋅10-3 H / 7,8 Ω = 6,41⋅10-4 Sek. (Ankerzeitkonstante)
Fs ( s ) =
k
0,622
=
(1 + sT1 ) ⋅ (1 + sT2 ) ⋅ (1 + sT3 ) (1 + 0,02s ) ⋅ (1 + 2 ⋅ 10 −3 s ) ⋅ (1 + 6,41 ⋅ 10 −4 s )
2) Übertragungsfunktion FR(s)
Die angegebene Schaltung stellt einen PI – Regler dar. Aus dem Merkblatt erhalten wir:

1 + sT1
1
1 

⋅
= k R 1 +
2 k S TS
s
 sTN 
TN
2 ⋅ 10 −2
mit TN = T1 = 0,02 Sek. , k R =
=
= 6,09
2k S TΣ 2 ⋅ 0,622 ⋅ 2,64 ⋅ 10 −3
TΣ = T2 + T3 = 2⋅10-3 Sek. + 6,41⋅10-4 Sek. = 2,64⋅10-3 Sek.
FR ( s ) =
1


FR ( s ) = 6,09 ⋅ 1 +
−2 
 2 ⋅ 10 s 
3) Dimensionierung von R1 und C1
R2 +
FR ( s ) =
1
sC1
R1
=
R2
R 
1
1 

+
= 2 ⋅ 1 +
R1 sR1C1 R1  sR2 C1 
Durch Koeffizientenvergleich erhalten wir:
R2/R1 = kR = 6,09 ==> R1 = R2/6,09 = 100 kΩ/6,09 = 16,42 kΩ ≈ 15 kΩ + 1k5 = 16,5 kΩ
R2C1 = TN = 2·10-2 Sek. ==>
C1 = 2·10-2 Sek./ R2 = 2·10-2 Sek./105Ω = 2·10-7 F ≈ 180 nF + 18 nF = 198 nF
R1a = 15k
R1b = 1k5
R1 = 16,5 kΩ
C1a = 180 nF
C1b = 18 nF
C1 = 198 nF
4) Tatsächliche Übertragungsfunktion FR(s)
kR = R2/R1 = 100 kΩ / 16,5 kΩ = 6,06
motortacho_rk_2.doc
Seite 3/4
Vanek 2006.04.08
DC-Servomotor mit Tachogenerator
TN = (R2C1) = (100 kΩ·198 nF) = 1,98·10-2 Sek.


1
FR ( s ) = 6,06 ⋅ 1 +

−2 
 1,98 ⋅ 10 s 
5) Sprungantwort
ANA, Zeit in Millisekunden:
in ms
6) Führungsgröße für 1000 U/min
Da ein Regler mit I-Anteil keine bleibende Regelabweichung besitzt, gilt für den stationären
Zustand:
uW(t → ∞) = uX(t → ∞) = ktg · 1000 U·min-1 = 0,00325 V/(U·min-1) · 1000 U·min-1 = 3,25V
motortacho_rk_2.doc
Seite 4/4
Vanek 2006.04.08