Übungen im Vortragen mit Demonstrationen (PC)

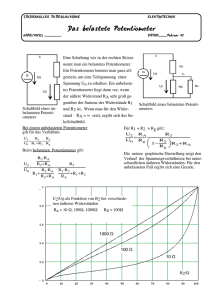
Sonnleitner Christiane
Übungen im Vortragen mit Demonstrationen
(PC)
15.10.2008
Elektrische Gleichströme II
1. Einleitung
Aus der Steckdose kommt, wie jeder weiß, Wechselstrom. Wenn wir ein Gerät im Haushalt in
Betrieb nehmen wollen, schließen wir es einfach an eine solche Steckdose an und es
funktioniert. Aber wenn alle Geräte mit Wechselstrom laufen, wozu benötigen wir dann
Gleichstrom? Ohne es richtig zu bemerken, verwenden wir jedoch täglich Gleichstrom. Jedes
Mal wenn wir den Zündschlüssel in unserem Auto umdrehen oder unser Handy einschalten.
Diese Geräte laufen auf Grund ihrer Halbleiterelemente nur mit Gleichstrom. Das Handy
beispielsweise wird zwar über eine normale Steckdose aufgeladen, jedoch wird schon im
Ladegerät der Wechselstrom gleichgerichtet und als Gleichstrom ins Handy eingespeist.
Gleichströme haben eine große Bedeutung in unserm alltäglichen Leben und daher wird im
folgenden Vortrag ein kurzer Überblick über die wesentlichen Schaltungen, Regeln und
Messmethoden im Zusammenhang mit elektrischen Gleichströmen vorgestellt.
2. Schaltungen
2.1 Reihen- und Parallelschaltung
[Tafelbild]
Reihenschaltung
Parallelschaltung
1
1
2
2
Stromstärke
IGes = I1 = I2
IGes = I1 + I2
Spannung
UGes = U1 + U2
UGes = U1 = U2
Widerstand
RGes = R1 + R2
Reihenschaltung:
Stromstärke: IGes = I1 = I2
Spannung: UGes = U1 + U2
Widerstand: RGes = R1 + R2
Parallelschaltung:
Stromstärke: IGes = I1 + I2
Spannung: UGes = U1 = U2
Widerstand: 1/RGes = 1/R1 + 1/R2
1/RGes = 1/R1 + 1/R2
2.2 Die Kirchhoff´schen Regeln
a) Knotenregel
An jedem Verzweigungspunkt (Knoten) in einer Schaltung muss ebenso viel Ladung zuwie abfließen. Die Summe aller Ströme in den einzelnen Zweigen, die in den Knoten
münden ist Null:
Σ Ii = 0
I0
I1
R1
Σ Ii = + I0 – I1 – I2 = 0
I2
R2
R3
b) Maschenregel
Die Gesamtspannung längs einer geschlossenen Masche einer Schaltung, d.h. die Summe
aller Spannungsabfälle an den einzelnen Elementen, aus denen die Masche besteht, ist
Null:
Σ Ui = 0
U0
U1
Σ Ui = U 0 – U1 = 0
R1
Σ Ui = U 0 – U2 – U3 = 0
U2
U3
R2
R3
Σ Ui = U 1 – U2 – U3 = 0
2.3 Die Spannungsteiler-Schaltung (Potentiometer)
a) Spannungsteilerregel
Um in dieser abgebildeten, einfachen Reihenschaltung die Teilspannung, die an einem der
beiden Widerstände abfällt unabhängig vom zweiten Widerstand berechnen zu können gibt es
die so genannte Spannungsteilerregel.
U0
R1
R2
U1
U2
Abb. …: Reihenschaltung zur Herleitung der Spannungsteilerregel
Die Spannungsteilerregel leitet sich wie folgt her:


U0 = U1 + U2 (Kirchhoffsche Maschenregel)
I1 = I2
U U
 nach dem Ohmschen Gesetz gilt: 1  2
R1 R2
nach U2 aufgelöst:


U 2  U1
[1]
R2
R1
[2]
R2
R1
R  R2
U 0  U1 1
R1
[3] durch U1 dividiert und Kehrwert gebildet:
U1/U0 = R1/RGes
U1
R
 1
mit RGes = R1 + R2
U 0 RGes
Spannungsteilerregel
[2] in [1] eingesetzt:
U 0  U1  U1
[3]
b) Versuch mit einem Potentiometer:
Damit man die beiden Widerstände leicht verstellt werden können, wird ein Schieberegler
eingebaut. Auf diese Weise kann Widerstand in zwei Teilwiderstände geteilt werden. So
einen Widerstand nennt man Potentiometer (Spannungsteiler).
Im Versuch wird nun ein solches Potentiometer an ein Netzgerät angeschlossen und an beiden
Enden mit je einem Spannungsmessgerät verbunden. Zusätzlich wird ein Lämpchen
eingebaut, um einen Kurzschluss zu verhindern, falls einer der beiden Teilwiderstände Null
wird. Der entsprechende Schaltplan ist in Abbildung … dargestellt:
U1
U2
Abb. …: Schaltplan einer Spannungsteilerschaltung zum Versuchsaufbau
Betätigt man nun den Schieberegler, so ändern sich die angezeigten Werte der
Spannungsmessgeräte proportional zueinander.
Stufenlose Einstellung der Stärke eines Lämpchens mit Hilfe eines Spannungsteilers
Material
7 Kabel mit Bananensteckern; 3 Krokodilklemmen; 1 Netzgerät; 2
Durchführung
Beobachtung
Erklärung
Spannungsmessgeräte; 1 Lämpchen; 1 Potentiometer
Aus dem Pluspol des Netzgerätes führt ein Kabel zum Pluspol des
Lämpchens. Vom Minuspol des Lämpchens führt ein Kabel zum
Potentiometer
(rechter
Anschluss)
und
eines
zum
ersten
Spannungsmessgerät
(Pluspol).
Der
Minuspol
des
ersten
Spannungsmessgerätes wird mit dem Pluspol des zweiten
Spannungsmessgerätes verbunden. Vom zweiten Spannungsmessgerät
(Minuspol) wiederum führt ein Kabel zum Potentiometer (linker
Anschluss) und ein anderes Kabel zurück zum Netzgerät (Minuspol). Der
mittlere Anschluss des Potentiometers wird mit dem Minuspol des ersten
Spannungsmessgerätes verbunden.
Hinweis: für mehr Übersicht empfiehlt es sich verschiedenfarbige Kabel
(z.B. rot und blau) zu verwenden.
Das Netzgerät in Betrieb nehmen und die Spannungsmessgeräte
einschalten. Der Regler am Potentiometer kann nun beliebig verstellt
werden und die Änderung der Werte der Spannungsmessgeräte kann
mitverfolgt werden.
Bei Betätigung des Reglers am Potentiometer ändern sich die Werte der
Spannungsabfälle an beiden Widerständen proportional zueinander.
Das Potentiometer entspricht zwei in Reihe geschalteten Widerständen.
U1
R
 1
Gemäß der Spannungsteilerregel
verhalten sich die
U 0 RGes
Teilspannungen proportional zu den Teilwiderständen. Somit ist die
Teilspannung umso kleiner (bzw. größer) je kleiner (bzw. größer) der
Teilwiderstand ist.
c) Anwendung eines Potentiometers
Anwendung finden Potentiometer zum Beispiel als Lautstärkeregler in einer Stereoanlage.
Auch in der Chemie gibt es eine sehr nützliche Anwendung. Mit Hilfe eines Kolbens als
Reaktionsgefäß, einer Spritze, einem Potentiometer und einem Computer mit der
entsprechenden Softwear ist es möglich den Verlauf einer Reaktion über die Zeit auf
zuzeichnen. Der Aufbau für einen solchen Versuch ist in Abbildung 1 dargestellt.
PC
Abb. …: Versuchsaufbau zur Nutzung eines Potentiometers zur Messung eines
Versuchsverlaufs
3. Messmethoden
3.1 Voltmeter
Um die Spannung zu messen, die an einem Verbraucher R abfällt muss man das Messgerät
parallel zu R schalten.
Die Spannung muss im Messgerät erst mittels eines Innenwiderstandes Ri in den
entsprechenden Strom übersetzt werden. Dieser Strom beträgt dann:
I = U/Ri
Der Übergang zu einem größeren Messbereich erfolgt durch Vergrößerung von Ri.
 Voltmeter müssen hochohmig sein!
100 kΩ
1000 V
100 V
9,9 kΩ
900 Ω
10 V
1V
100 Ω
10 mA
R
U0
Abb. …: Schaltplan eines Voltmeters
3.2 Amperemeter
Um den Strom zu messen, der durch einen Verbraucher R fließt muss man das Messgerät in
Reihe zu R schalten.
Der Übergang zu einem größeren Messbereich erfolgt durch zuschalten
Parallelwiderstandes(Shunt) durch den der Strom am Messgerät vorbeigeleitet wird.
 Amperemeter müssen niedrigohmig sein!
eines
100 mA
10 mA
11,1 Ω
1A
1,01 Ω
10 A
0,1 Ω
100 Ω
R
U0
10 mA
Abb. …: Schaltplan einer Amperemeters
3.3 Wheatstone´sche Brückenschaltung zur Messung ohmscher Widerstände
Würde man einen Widerstand durch die Messung von U und I bestimmen, so würde die
Messung durch die endlichen Widerstände der Messgeräte sehr ungenau. Um dies zu
vermeiden misst man den Widerstand stromlos mittels einer Wheatstonschen
Brückenschaltung.
I1
A
R1
Rx
R2
R3
B
I2
U0
Abb. …: Schaltplan einer Wheatstone´schen Brücke
 Rx ist gesucht
 Es muss U1 = U2 gelten
 R3 ist variabel
 wenn Ux = U3 ist, dann ist zwischen A und B keine Spannung mehr vorhanden
 durch das Messgerät zwischen A und B fließt kein Strom
 der Strom I1 geht vollständig weiter durch Rx daraus folgt:
I2R3 = I1Rx und I1R1 = I2R2
R x = R3
R1
R2
4. Schluss
Nachdem man jetzt ein bisschen mehr über elektrischen Gleichstrom weiß, kann man sich
auch einen richtigen Schaltplan ansehen. Dabei wird man jedoch feststellen, dass so ein echter
Schaltplan, beispielsweise vom Auto, sehr viel komplizierter ist, als erwartet. Der Schaltplan
eines Autos besteht aus mehreren Seiten und sieht auf den ersten Blick sehr verwirrend aus.
Aber trotz allem gelten auch in einem solchen Plan die Regeln von Kirchhoff und das
Ohmsche Gesetz genauso wie für die einfachste Reihen- und Parallelschaltung.
5. Literatur
- Stuart, Klages, Kurzes Lehrbuch der Physik, 18. Auflage, Springer, 2006
- Gerthsen, Physik, H. Vogel, 22. Auflage, Springer, 2004