Lösungen

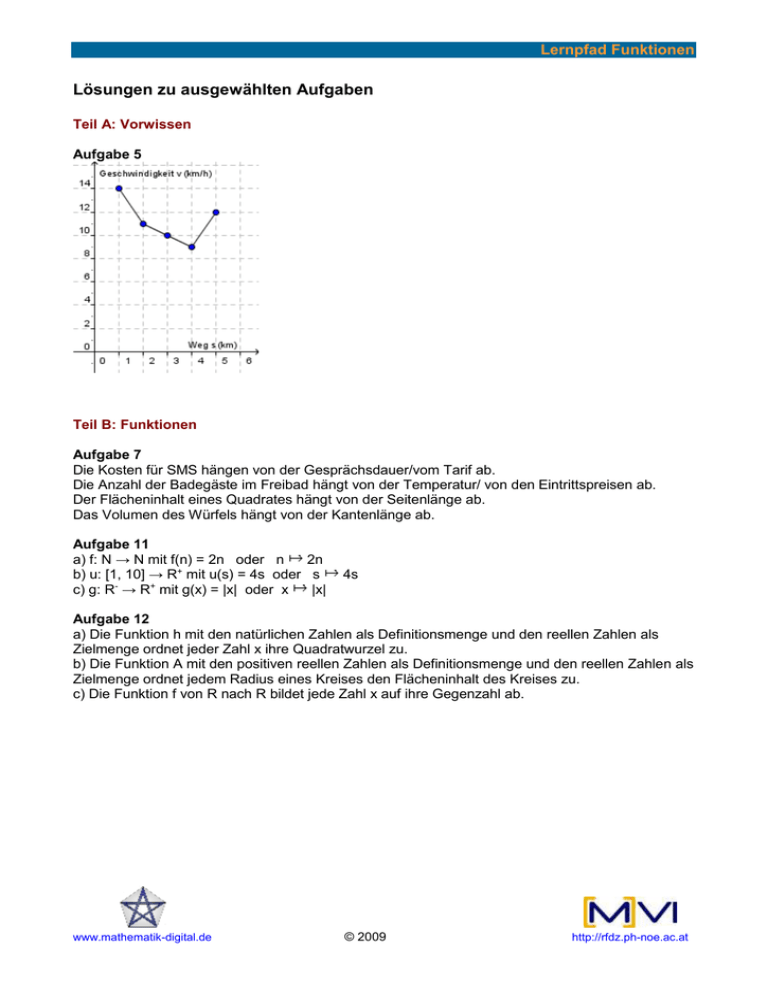
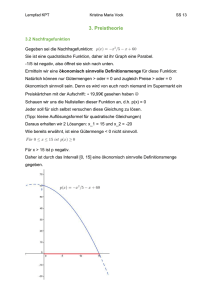
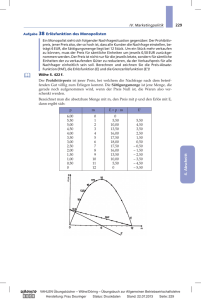
Lernpfad Funktionen
Lösungen zu ausgewählten Aufgaben
Teil A: Vorwissen
Aufgabe 5
Teil B: Funktionen
Aufgabe 7
Die Kosten für SMS hängen von der Gesprächsdauer/vom Tarif ab.
Die Anzahl der Badegäste im Freibad hängt von der Temperatur/ von den Eintrittspreisen ab.
Der Flächeninhalt eines Quadrates hängt von der Seitenlänge ab.
Das Volumen des Würfels hängt von der Kantenlänge ab.
Aufgabe 11
a) f: N → N mit f(n) = 2n oder n
2n
b) u: [1, 10] → R+ mit u(s) = 4s oder s
c) g: R- → R+ mit g(x) = |x| oder x
|x|
4s
Aufgabe 12
a) Die Funktion h mit den natürlichen Zahlen als Definitionsmenge und den reellen Zahlen als
Zielmenge ordnet jeder Zahl x ihre Quadratwurzel zu.
b) Die Funktion A mit den positiven reellen Zahlen als Definitionsmenge und den reellen Zahlen als
Zielmenge ordnet jedem Radius eines Kreises den Flächeninhalt des Kreises zu.
c) Die Funktion f von R nach R bildet jede Zahl x auf ihre Gegenzahl ab.
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
Teil C: Grundtypen
Aufgabe 38
a) d = 80; k = 4
b) f(x) = 4x + 80
c) f(x) = 5x + 60
Aufgabe 39
a) a = 1,04 und c = 80
b) f(x)=80*1,04^x
c) f(x) = 60*1,05^x
Aufgabe 40
Angebot A Angebot B
nach 1 Monat
84,00
83,20
nach 2 Monaten
88,00
86,53
nach 3 Monaten
92,00
89,99
nach 4 Monaten
96,00
93,59
nach 5 Monaten
100,00
97,33
nach 6 Monaten
104,00
101,23
nach 7 Monaten
108,00
105,27
nach 8 Monaten
112,00
109,49
nach 9 Monaten
116,00
113,86
nach 10 Monaten 120,00
118,42
nach 11 Monaten 124,00
123,16
nach 12 Monaten 128,00
128,08
Summe
1272,00
1250,15
Im ersten Jahr ist Angebot A besser.
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
Aufgabe 41
nach … Monaten Angebot A Angebot B
1
84,00
83,20
2
88,00
86,53
3
92,00
89,99
4
96,00
93,59
5
100,00
97,33
6
104,00
101,23
7
108,00
105,27
8
112,00
109,49
9
116,00
113,86
10
120,00
118,42
11
124,00
123,16
12
128,00
128,08
13
129,00
133,21
14
130,00
138,53
15
131,00
144,08
16
132,00
149,84
17
133,00
155,83
18
134,00
162,07
19
135,00
168,55
20
136,00
175,29
21
137,00
182,30
22
138,00
189,59
23
139,00
197,18
24
140,00
205,06
25
141,00
213,27
26
142,00
221,80
27
143,00
230,67
28
144,00
239,90
29
145,00
249,49
30
146,00
259,47
31
147,00
269,85
32
148,00
280,64
33
149,00
291,87
34
150,00
303,55
35
151,00
315,69
36
152,00
328,31
37
153,00
341,45
38
154,00
355,11
39
155,00
369,31
40
156,00
384,08
41
157,00
399,44
42
158,00
415,42
43
159,00
432,04
44
160,00
449,32
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
45
46
47
48
161,00
162,00
163,00
163,00
467,29
485,99
505,43
525,64
Angebot B ist langfristig besser.
Aufgabe 42
(1) Kapitalwachstum bei Anlage mit Zinseszins => exponentiell
(2) Handytarif mit Grundgebühr und sekundengenauer Abrechnung => linear
(3) Fortgesetzte Verdopplung eines Wetteinsatzes => exponentiell
(4) Gesamtkosten einer Produktionsmaschine mit Anschaffungskosten und laufenden Materialund Wartungskosten => kann nicht entschieden werden
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
Lernzielkontrolle
1) a) R(t) = 15 + 0,05t
Zeit t
0
1
2
3
4
5
6
Kosten R
15,00
15,05
15,10
15,15
15,20
15,25
15,30
b) Kein indirektes Verhältnis, da mit der Zeit auch die Kosten zunehmen.
Kein direktes Verhältnis, da die Gerade nicht durch den Ursprung geht, die Konstante d nicht
null ist und dem k-Fachen von t nicht das k-Fache von R entspricht.
2) a) Steigung, Anstieg
b) durch den Punkt (0|d)
c) wenn k > 0
d) wenn k < 0
e) eine zur x-Achse parallele Gerade
3) Eine Funktion ist eine eindeutige Zuordnung.
eine Zuordnungsvorschrift, die jedem Argument eindeutig einen Funktionswert zuordnet
Definitionsmenge
Zielmenge
4) (4) ist direkt proportional.
(1) ist indirekt proportional.
(2) und (4) wachsen linear.
(3) wächst exponentiell.
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
Teil D: Anwendungen
Aufgabe 47
Anm.: Kostenfunktion f(x) = 0.01 x³ - 9 x² + 3000 x + 100000
a)
f(200) = 420 000
f(400) = 500 000
f(600) = 820 000
f(800) = 1 860 000
f(1000) = 4 100 000
Die Kosten nehmen mit höheren Stückzahlen zu.
b) Auch wenn nichts produziert wird, gibt es Fixkosten: 100 000 Euro.
Aufgabe 48
c) d = Fixkosten, k = variable Kosten pro Stück
Aufgabe 49
a) d = 0; k ist positiv
b) 4000 Euro
c) bei x = 64,9 (also bei etwa 65 Stück) und bei x = 990,7 (also bei etwa 991 Stück); Kosten und
Erlös sind gleich groß;, kein Verlust/kein Gewinn
Aufgabe 50
a) Die Stellen der Schnittpunkte von Kosten- und Erlösfunktion entsprechen den Nullstellen der
Gewinnfunktion.
b) Break-even-Point: ab hier wird Gewinn gemacht. Schnittpunkt zwischen Kosten- und
Erlösfunktion, ab dem der Erlös größer als die Kosten ist.
c) Gewinnzone von 65 (aufrunden!) bis 990 (abrunden!) Stück
d) mindestens 65 Stück
Aufgabe 51
Höherer Preis => bei geringerer Stückzahl bereits Gewinn
Gewinnzone ist breiter
größerer Gewinn
Produkt wird weniger gekauft, da es teurer ist.
Aufgabe 52
Senkung der Fixkosten => größerer Gewinn, Gewinnzone breiter
Aufgabe 53
K(x) = 100 000 + 2x
E(x) = 6x
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
K(x) = E(x) => x = 25 000 => Der Break-even-Point liegt bei 25 000 Stück.
Aufgabe 54
Preis
100
150
200
250
300
350
400
450
500
550 600 650 700
Menge 19000 18000 17000 16000 15000 14000 13000 12000 11000 10000 9000 8000 7000
Aufgabe 55
a) je höher der Preis desto geringer die Nachfrage
b) bei Prestige-Produkten, je teurer desto exklusiver
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
Aufgabe 56
a) (0|21 000) Nachfrage, wenn das Produkt nichts kostet
(1050|0)
Preis, bei dem niemand mehr das Produkt kauft
b) Preis und Nachfrage können nur positive Werte annehmen.
Aufgabe 57
Sättigungsmenge bei 21 000 Stück; Höchstpreis bei 1050,- €.
Aufgabe 58
n(300) = 15 000; n(350) = 14 000
Aufgabe 59
Der Höchstpreis, bei welchem die Nachfrage gleich null ist, liegt bei 1050,-€.
Die Sättigungsmenge, also jene Menge, die bei einem Preis von 0,- € nachgefragt wird, beträgt 21
000 Stück.
Aufgabe 60
a) Abnahme um 250 Packungen
b)
Preis (Euro)
1
Nachfrage (Stück)
1750
c)
www.mathematik-digital.de
2
1500
© 2009
3
1250
4
1000
5
750
6
500
http://rfdz.ph-noe.ac.at
Lernpfad Funktionen
d) n(p) = 2000 – 250p, D = [0,8], Zielmenge = R+0
e) Sättigungsmenge n(0) = 2000
=> Es werden maximal 2000 Stück nachgefragt.
Höchstpreis
n(p) = 0 => p = 8
=> Der Höchstpreis, bei dem niemand mehr das Produkt kauft, beträgt 8 Euro.
www.mathematik-digital.de
© 2009
http://rfdz.ph-noe.ac.at