Document

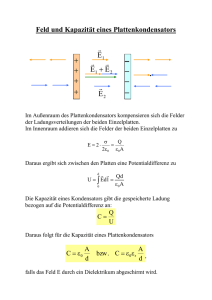
Physikprotokoll
Mittwoch, 7.11.07
Protokollant: Anastasia Homann
Zu Beginn der Unterrichtseinheit stellt Herr Legleitner zwei Fragen, die wir
"empirisch" und deduktiv zu beantworten versuchen:
1- Wovon hängt die Kapazität eines Plattenkondensators ab?
2- Wie hängt das elektrische Feld von den Ladungen des Plattenkondensators ab?
Bild: Homogenes elektrisches Feld zwischen zwei Kondensatorplatten mit der
Ladung Q+ und Q1.
1.1
Da wir die erste Frage deduktiv beantworten wollen, schauen wir uns Gesetze an, die
ein homogenes elektrisches Feld beschreiben:

Gesetz zur Kapazität C eines Plattenkondensators:

Gesetz zur Spannung U eines Plattenkondensators:
U=E*d

Und das bei der Hausarbeit zum Mittwoch erarbeitete Gesetz zur Flächendichte
(Sigma):
Q/A


[] = 1 C/m2
= konstant
Laut der Formel ist die Ladung der Kondensatorplatten Q proportional zur Fläche der
Platten A, d.h. :
Je größer die Fläche, desto größer die Anzahl der Ladungen auf der Oberfläche der
Kondensatorplatten.
Die elektrische Feldkonstante  in der Luft definiert man folgendermaßen :
 = /E
[]=C/(Vm)
1.2
Im Folgenden beziehen wir uns auf das Arbeitsblatt "Kapazität eines
Plattenkondensators" und den dazu gemachten Versuch zur Werterfassung der
Ladung Q für verschiedene Spannungen (U). Für die deduktiv erstellte Tabelle
(s.unten) benutzen wie die Werte für die Spannung U und die dazugehörige Ladung Q
aus dem angesprochenen Versuch. Zwei Größen sind dabei konstant:
Fläche der Kondensatorplatten A=0,080089m²,
Abstand zwischen den Platten d=0,008m.
Dazu stellen wir die Formel U=E*d (s.Seite1) nach E um:
E=U/d
[E]=V/m
1.Messung
2.Messung
3.Messung
E in V/m
62500
125000
187500
Q/A in C/m²
5,99*10^-7
12,24*10^-7
17,73*10^-7
 = /E in
C/(V*m)
9,584*10^-12
9,792*10^-12
9,456*10^-12
Der somit ermittelte Mittelwert für  ist 9,61*10^-12. Aus der Literatur ist uns
jedoch der Wert = 8,85 · 10-12 C/(Vm) bekannt (vgl. "Physik", Dorn-Bader,
Schroedel Verlag, Hannover, 2000: s.12). Die Ungenauigkeit unseres Wertes ist auf
Messfehler zurückzuführen, wie auch die Feuchtigkeit der Luft u.s.w.
MERKE!
Die Flächendichte der felderzeugenden Ladung eines homogenen Feldes ist zu
seiner Feldstärke E proportional (vgl. Tabelle!). Wenn wir die Gleichung  = /E
nach umstellen, dann gilt bei der Luft als Medium  *E mit der elektrischen
Feldkonstanten  =8,85*10^-12 C/(Vm)
Wir formen die bekannten Formeln um , um auf die Kapazität des elektrischen Feldes
C in Abhängigkeit von zu kommen:
Q/A
 *E
Q/A= *E
E=U/d
Q=C*U
(C*U)/A= *(U/d)
Wir kürzen die Formel mit U (d.h. mit U dividieren) und stellen sie nach der
Kapazität C um.
C= d
Hiermit haben wir die Kapazität eines Plattenkondensators mit der Fläche A und dem
Plattenabstand d bei einem homogenen Feld deduktiv herausgearbeitet. Da
konstant ist, verändert sich die Kapazität C mit der Fläche der Kondensatorplatten
(proportional) und mit dem Abstand der Platten (antiproportional). Dies beweist auch
folgende Tabelle und die Graphen (bitte das Blatt querlegen!):