Die geradlinig gleichförmige Bewegung

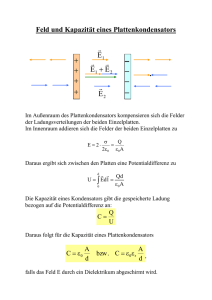
12 Physik
12-1 Felder
12-1-2 Elektrisches Feld
12-1-2-7 Kapazität des Kondensators
Was versteht man unter der Kapazität eines Kondensators?
110-111/Kapitel 4.1.7
Formeln auf S.135, Kondensatoren
Befindet sich auf einem Plattenkondensator die Ladung Q, so entsteht ein
homogenes elektrisches Feld zwischen den Kondensatorplatten.
+
-
+
-
+
-
+
-
Das elektrische Feld führt zu einer Spannung U  E  d zwischen den Kondensatorplatten.
Verdoppeln wir die Ladung auf den Kondensatorplatten auf 2Q, so verdoppelt sich auch die
elektrische Feldstärke E und damit die Spannung U zwischen den Kondensatorplatten.
+
+
+
+
+
+
+
+
-
Die Ladung ist proportional zur Spannung ( Q  U ), sofern sich die Geometrie (Plattenfläche
A und Abstand der Platten d) des Kondensators nicht ändert.
Durch die Proportionalität zwischen der Ladung Q und der Spannung U liefert der Quotient
Q
bei unveränderter Geometrie des Kondensators einen konstanten Wert. Wir nennen den
U
Q
Quotienten
die Kapazität des Kondensators. Sie beschreibt, wie viel Ladung ein
U
Kondensator bei gegebener Spannung speichert, d.h. welche Ladungskapazität ein
Kondensator besitzt.
Die Kapazität C eines Kondensators ist definiert durch den Quotienten C 
Q
U
As
Q 
Die Einheit der Kapazität ist C      1
 1Farad  1F , zu Ehren des englischen
V
U 
Naturforschers MICHAEL FARADAY (1791-1867).
Versuch zur Proportionalität zwischen der Ladung Q und der Spannung U mit
einem Plattenkondensator mit runden Platten (Durchmesser =260mm,
Plattenabstand d=5mm) und den Spannungen U1  100V und U 2  200V . Die
Ladungsmessung erfolgt mit einem Messverstärker.
Verdoppeln wir bei konstanter Spannung U den Flächeninhalt A der Platten eines
Plattenkondensators, so muss sich die Ladung Q verdoppeln, um die elektrische
Feldstärke innerhalb der Platten konstant zu halten.
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
+
-
Durch den doppelten Flächeninhalt A der Platten verdoppelt sich die Kapazität des
Plattenkondensators:
Q
2Q
 C  Verdoppelung des Flächeninhaltes A 
 2C
U
U
Wird der Plattenabstand d bei konstanter Ladung Q verdoppelt, so verdoppelt sich auch die
Spannung U zwischen den Platten (siehe Aufgabe 3 des letzten Kapitels). Die Kapazität des
Plattenkondensators halbiert sich:
Q
Q
1
 C  Verdoppelung des Plattenabstandes d 
 C
U
2U 2
Die Kapazität eines Plattenkondensators ist proportional zum Flächeninhalt A und umgekehrt
proportional zum Plattenabstand d.
Für die Kapazität C eines Plattenkondensators gilt C   0
 0 heißt elektrische Feldkonstante.
A
d
Die elektrische Feldkonstante  0 (epsilon null) ist eine Naturkonstante. Sie hat den Wert
As
.
 0  8,854  10 12
Vm
Versuch zur Bestimmung der elektrischen Feldkonstante mit einem
Plattenkondensator mit runden Platten (Durchmesser =260mm,
Plattenabstand d=5mm) und der Spannung U  100V . Die Ladungsmessung
erfolgt mit einem Messverstärker.
1. 117/9
1.
a. Aus U  E  d folgt E 
U 2000V
V

 50000
d
0,04m
m
b. Die Kapazität beträgt
A
As 0,03m 2
As
 8,854  10 12

 6,64  10 12
 6,64  10 12 F  6,64 pF
d
Vm 0,04m
V
Q
As
Aus C 
folgt Q  C  U  6,64  10 12
 2000V  1,33  10 8 As
U
V
Die Flächenladungsdichte gibt die Ladung pro Flächeninhalt an. Wir verwenden den
griechischen Buchstaben  (gesprochen sigma)
Ladung
Q 1,33  10 8 As
As

 
 4,43  10 7 2
2
Flächeninh alt A
0,03m
m
W
c. Aus U 
folgt W  U  q  2000V  10 8 C  2  10 5 J
q
d. Wenn die Spannungsquelle abgetrennt ist, kann keine Ladung mehr zu- oder abfließen.
Die elektrische Feldstärke verändert sich daher nicht, wenn der Plattenabstand
verdoppelt wird (siehe Aufgabe 3 des letzten Kapitels). Nach der Formel U  E  d
C  0
verdoppelt sich die Spannung bei konstanter Feldstärke E und doppeltem Plattenabstand d. Die
benötigte Energie für den Transport der Probeladung verdoppelt sich dann ebenfalls.
e. In den eingebrachten kleinen Platten findet Influenz statt. Es werden Ladungen an die
Außenflächen der kleinen Platten verschoben, damit kein elektrisches Feld in die
leitenden kleinen Platten eindringen kann. Um das elektrische Feld des
Plattenkondensators komplett abzuschirmen, muss die Flächenladungsdichte auf den
Oberflächen der kleinen Platten genauso groß sein wie auf den großen Platten des
Plattenkondensators. Die von den Quellen der großen Platten ausgehenden Feldlinien
verschwinden dadurch komplett in den Senken der kleinen Platten.
Q
As
Aus   folgt Q    A  4,43  10 7 2  0,002m 2  8,86  10 10 As
A
m