Vorlesung 10: Wasserkraft und Landwirtschaft
Werbung

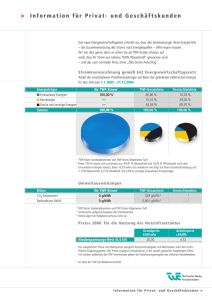
Übersicht 1 Wasserkraft: Herausforderungen CH 2 Wasserkraft und Landwirtschaft: Problemstellung 3 Model 4 Ergebnisse Vorlesung 10: Wasserkraft und Landwirtschaft 1/9 Wasserkraft CH: Herausforderungen Geplanter Ausbau der Kapazität bis 2050 um 10 TWh (4TWh ohne Pumpspeicher) Probleme: Konflikt mit Gewässerschutz (Restwassermengen werden neu verhandelt) Noch unsicherer Einfluss des Klimawandels Einsprachen, viele Grossprojekte nur schwer durchsetzbar Hoher Bedarf für Pumpspeicher in Europa durch Ausbau Wind/Solar Netzausbau ⇒ Sind die Rahmenbedingungen für zusätzliche Investitionen hinreichend? Vorlesung 10: Wasserkraft und Landwirtschaft 2/9 Wasserkraft und Landwirtschaft: Problemstellung In vielen Ländern besteht eine Konkurrenz in der Wassernutzung zwischen Wasserkraft und Landwirtschaft. Die Konkurrenz entsteht dabei häufig nicht aus rivalisierender Nutzung der Wassermenge an sich sondern aus unterschiedlichen Zeitprofilen der Nutzung. Landwirtschaft Wasserbedarf folgt den Wachstumsperioden (Wasser vorwiegend im Frühjahr und Sommer nützlich) Wasserkraft Stromproduktion hängt von Menge und Fallhöhe ab Produktion am sinnvollsten, wenn hohe Stromnachfrage besteht (CH: Winter) Vorlesung 10: Wasserkraft und Landwirtschaft 3/9 Modell Stromproduktion aus Wasserkraft: Z MWH = E R(t)H(t)dt mit R(t) ≥ R 0 : Wasserabfluss, H(t) = h(V (t)): Fallhöhe, V̇ (t) = F (t) − R(t): Speichermenge, F (t): Zufluss Gewinnfunktion: Φ(R(t), H(t)|Po(t), t) = maxPr (t) (Pr (t) − Po(t))D(Pr (t), t) Vorlesung 10: Wasserkraft und Landwirtschaft + (Po(t) − c)MWH(t) 4/9 Modell Landwirtschaft, Wachstum der Nutzpflanzen: Ṡ(t) = g(S(t), W (t), X (t)) mit W (t) ≤ R(t): Bewässerung, Preis c2 X (t): Landwirtschaftliche Inputs mit Preis c1 , P: Preis für den Output, Vorlesung 10: Wasserkraft und Landwirtschaft 5/9 Modell Gesucht wird eine optimale Lösung für ein Jahr. Optimiert wird der Gewinn aus der landwirtschaftlichen Tätigkeit zzgl. dem Gewinn aus dem Stromverkauf. Vorlesung 10: Wasserkraft und Landwirtschaft 6/9 Modell: Lösungsansatz Es liegt ein optimal control Problem mit bewertetem aber freiem Endzustand S(T ) vor. Es gibt zwei statische Nebenbedingungen, die zu allen Zeitpunkten erfüllt sein müssen W (t) ≤ R(t), R(t) ≥ R 0 . Ansatz: Hamiltonfunktion aufstellen und die Nebenbedingungen mit zusätzlichen (statischen) Hilfsvariablen µ, δ berücksichtigen. Vorlesung 10: Wasserkraft und Landwirtschaft 7/9 Ergebnis ∂g − c2 λ2 = δ + (Po(t) − c) (E h(V (t))) + λ1 ∂W Bedingung setzt den Schattenpreis von Wasser im Reservoir (λ2 ) gleich dem Schattenpreis der Einhaltung der Restwassermenge (δ) zuzüglich dem Grenzgewinn aus einer Einheit Stromproduktion zum Zeitpunkt t ((Po(t) − c) (E h(V (t)))) zuzüglich dem Nettoeffekt einer zusätzlichen Einheit ∂g Wasser für Bewässerung ( λ1 ∂W − c2 ). Vorlesung 10: Wasserkraft und Landwirtschaft 8/9 Schlussfolgerungen Auch wenn keine Nutzungskonflikte bzgl. der Menge einer Ressource vorliegen, können Nutzungskonflikte bzgl. des Zeitpunktes der Nutzung erheblich sein. Wasserkraft und Landwirtschaft sind ein Beispiel hierfür. Ein optimales Management erfordert dabei einen Ausgleich zwischen den Interessen der Wassernutzer. In der Praxis dominiert in vielen Ländern ein Interesse (Wasserkraft, Bewässerung, Gewässerschutz). Für die Schweiz ist bedeutsam, dass die Wünsche für einen Ausbau der Wasserkraft nicht vollständig kompatibel mit anderen Anforderungen (Gewässerschutz, Landwirtschaft) sind. Vorlesung 10: Wasserkraft und Landwirtschaft 9/9