Formelsammlung als PDF herunterladen

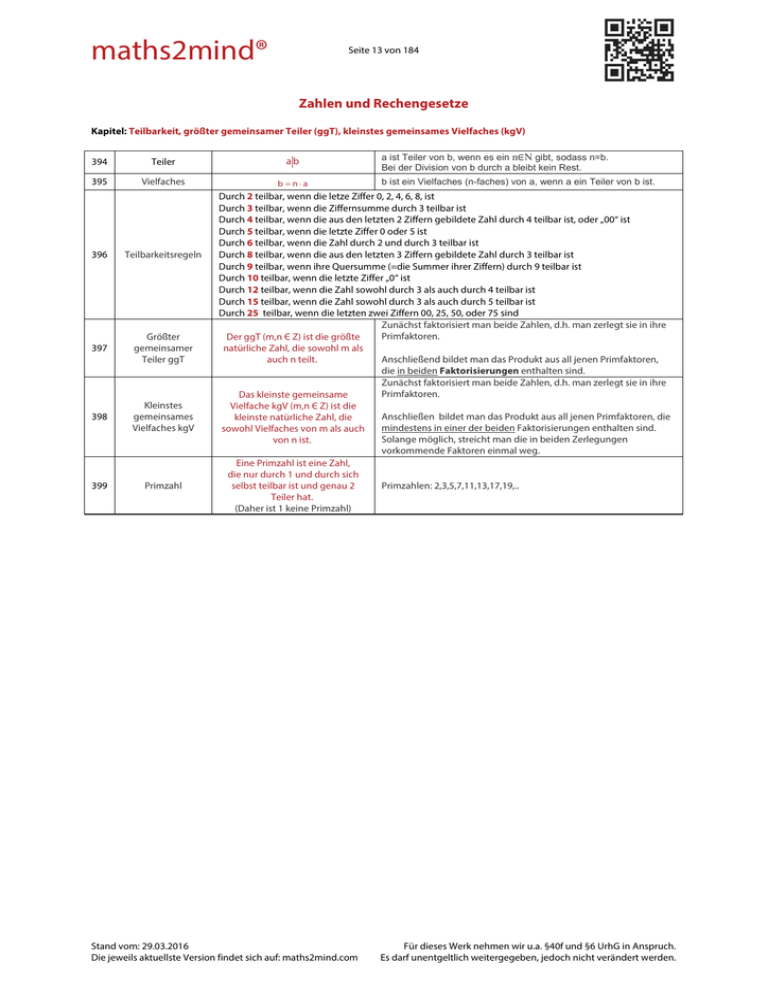
maths2mind®
Seite 13 von 184
Zahlen und Rechengesetze
Kapitel: Teilbarkeit, größter gemeinsamer Teiler (ggT), kleinstes gemeinsames Vielfaches (kgV)
394
Teiler
395
Vielfaches
396
Teilbarkeitsregeln
397
Größter
gemeinsamer
Teiler ggT
398
Kleinstes
gemeinsames
Vielfaches kgV
399
Primzahl
ab
b  na
a ist Teiler von b, wenn es ein n∈N gibt, sodass n=b.
Bei der Division von b durch a bleibt kein Rest.
b ist ein Vielfaches (n-faches) von a, wenn a ein Teiler von b ist.
Durch 2 teilbar, wenn die letze Ziffer 0, 2, 4, 6, 8, ist
Durch 3 teilbar, wenn die Ziffernsumme durch 3 teilbar ist
Durch 4 teilbar, wenn die aus den letzten 2 Ziffern gebildete Zahl durch 4 teilbar ist, oder „00“ ist
Durch 5 teilbar, wenn die letzte Ziffer 0 oder 5 ist
Durch 6 teilbar, wenn die Zahl durch 2 und durch 3 teilbar ist
Durch 8 teilbar, wenn die aus den letzten 3 Ziffern gebildete Zahl durch 3 teilbar ist
Durch 9 teilbar, wenn ihre Quersumme (=die Summer ihrer Ziffern) durch 9 teilbar ist
Durch 10 teilbar, wenn die letzte Ziffer „0“ ist
Durch 12 teilbar, wenn die Zahl sowohl durch 3 als auch durch 4 teilbar ist
Durch 15 teilbar, wenn die Zahl sowohl durch 3 als auch durch 5 teilbar ist
Durch 25 teilbar, wenn die letzten zwei Ziffern 00, 25, 50, oder 75 sind
Zunächst faktorisiert man beide Zahlen, d.h. man zerlegt sie in ihre
Primfaktoren.
Der ggT (m,n Є Z) ist die größte
natürliche Zahl, die sowohl m als
Anschließend bildet man das Produkt aus all jenen Primfaktoren,
auch n teilt.
die in beiden Faktorisierungen enthalten sind.
Zunächst faktorisiert man beide Zahlen, d.h. man zerlegt sie in ihre
Primfaktoren.
Das kleinste gemeinsame
Vielfache kgV (m,n Є Z) ist die
Anschließen bildet man das Produkt aus all jenen Primfaktoren, die
kleinste natürliche Zahl, die
mindestens in einer der beiden Faktorisierungen enthalten sind.
sowohl Vielfaches von m als auch
Solange möglich, streicht man die in beiden Zerlegungen
von n ist.
vorkommende Faktoren einmal weg.
Eine Primzahl ist eine Zahl,
die nur durch 1 und durch sich
selbst teilbar ist und genau 2
Primzahlen: 2,3,5,7,11,13,17,19,..
Teiler hat.
(Daher ist 1 keine Primzahl)
Stand vom: 29.03.2016
Die jeweils aktuellste Version findet sich auf: maths2mind.com
Für dieses Werk nehmen wir u.a. §40f und §6 UrhG in Anspruch.
Es darf unentgeltlich weitergegeben, jedoch nicht verändert werden.