Übungszettel für die 2. Klasse: Brüche in Textgleichungen

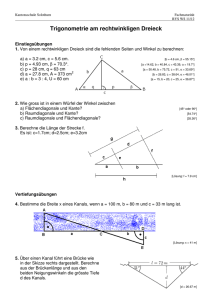
Übungszettel für die 2. Klasse:
Brüche in Textgleichungen
(1)
Addiert man zur Hälfte einer Zahl das Viertel dieser Zahl, so ergibt sich
a) 6, b) 9, c) 15, d) 21, e) 66. Berechne die Zahl!
(2)
Subtrahiert von der Hälfte einer Zahl das Viertel dieser Zahl, so ergibt sich
a) 10, b) 7, c) 14, d) 23, e) 46, f) 55. Berechne die Zahl!
(3)
Addiert man zur Hälfte einer zahl das Drittel dieser Zahl, so ergibt sich
a) 10, b) 15, c) 25, d) 30, e) 35, f) 55. Berechne die Zahl!
(4)
Subtrahiert man vom Drittel einer Zahl das Viertel dieser Zahl, so ergibt sich
a) 1, b) 3, c) 4, d) 7, e)10, f) 19. Berechne die Zahl!
(5)
Addiert man zu einer Zahl die um1 größere Zahl, so ergibt sich
a) 7, b)11, c) 15, d) 19, e) 25. Berechne die Zahl!
(6)
Addiert man zu einer Zahl die um 5 größere Zahl, so ergibt sich 13, b) 21, c) 29,
d) 37, e) 61. Berechne die Zahl!
(7)
Addiert man zum
a) 3fachen, b) 4fachen, c) 5fachen, d) 12fachen einer Zahl die Zahl 5, so ergibt
sich 65. berechne die Zahl!
(8)
In einem rechtwinkeligen Dreieck, ist der eine Spitze Winkel
a) doppelt, b) 4mal, c) 5mal, d) mal, e) 14mal so groß wie der andere spitze
Winkel. Berechne die spitzen Winkel dieses Dreiecks!
(9)
Ein Außenwinkel eines Winkels ist a) 3mal, b) 4mal, c) 9mal, so groß wie sein
zugehöriger Innenwinkel. Berechne diesen Innenwinkel und seinen
Außenwinkel!
(10) In einem Parallelogramm ist der eine Winkel a) 2mal, b) 5mal, c) 8mal, d) 11mal
so groß wie der andere Winkel. Berechen die Winkel des Parallelogramms!
(11) Der Umfang eines gleichschenkligen Dreiecks beträgt 90 m, ein Schenkel ist
a) 2mal, b) 4mal, c) 7mal so lang wie die Basis. Berechne die Längen der
Dreiecksseiten!
(12) Der Winkel an der Spitze eines gleichschenkligen Dreiecks ist a) 3mal, b) 7mal,
c) 13mal so groß wie ein Basiswinkel. Berechne die Winkel des Dreiecks!
(13) Ein Basiswinkel eines gleichschenkligen Dreiecks ist a) doppelt, 4mal, c) 7mal
so groß wie der Winkel an der Spitze. Berechne die Winkel des Dreiecks!
(14) Der Umfang eines Dreiecks beträgt 120 m; die Länge ist a) das Doppelte,
3fache, c) 4fache, d) 5fache, e) 9fache, f) 11fache der Breite. Berechne die
Länge sowie die Breite eines solchen Dreiecks!
(ue2-brueche-txtglg.doc)
bna Helmut Bineder
1/2
(15) Der Umfang eines Rechtecks beträgt 100 m. die Länge ist um
a) 2 m, 4 m, c) 6 m, d) 10 m größer als die Breite. Berechne die Länge sowie die
Breite eines solchen Dreiecks.
(16) Der Umfang eines Rechtecks beträgt 150m.
Die Breite a) 6m, b) 10m, c) 14m d) 22m kürzer als die Länge. Berechne die
Länge sowie die Breite eines solchen Rechtecks!
(17) Zwei Brüder sind zusammen a) 16, b) 20, c) 22, d) 24, e) 30 Jahre alt; die eine
ist um 2 Jahre älter als der andere. Berechne das Alter jeder dieser Knaben!
(18) Zwei Schwestern sind zusammen a) 17, b) 21, c) 25, d) 33 Jahre alt; die eine ist
um 3 Jahre älter als die andere. Berechne das Alter jeder dieser Schwestern!
(19) Eine Klasse hat 30 Schüler; es sind um 4 Knaben mehr als Mädchen.
Berechne, wie viel Knaben und wie viel Mädchen eine solche Klasse hat!
Berechne ebenso: b) 29 Schüler, 3 Knaben mehr. c) 28 Schüler, 6 Knaben
mehr, d) 27 Schüler, 7 Knaben mehr.
(20) Vater und Sohn sind gemeinsam 44 Jahre alt; der Vater ist um 22 Jahre älter
als der Sohn. Berechne das Alter des Vaters und das des Sohnes!
Berechne ebenso:
b) zusammen 49 Jahre, Vater 25 Jahre älter;
c) zusammen 68 Jahre; Vater 40 Jahre älter.
(21) Ein Anhänger kostet samt Halskette 350 €; die Halskette kostet 1/4 des
Gesamtbetrags. Berechne, wie viel der Anhänger und wie viel die Halskette
kostet!
(22) Ein Armband kostet samt Halskette 360 €; die Kosten für das Armband
betragen 1/8 des Kaufpreises. Berechne, die Einzelpreise für jedes
Schmuckstück!
(ue2-brueche-txtglg.doc)
bna Helmut Bineder
2/2