Trigonometrie am rechtwinkligen Dreieck

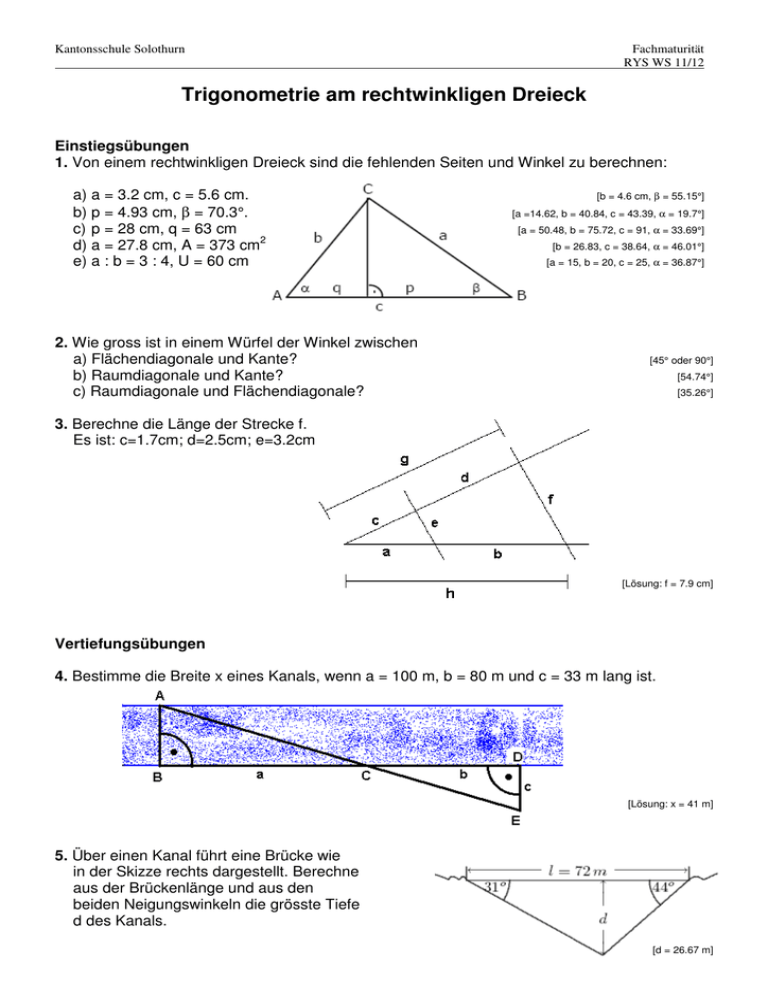
Kantonsschule Solothurn
Fachmaturität
RYS WS 11/12
Trigonometrie am rechtwinkligen Dreieck
Einstiegsübungen
1. Von einem rechtwinkligen Dreieck sind die fehlenden Seiten und Winkel zu berechnen:
a) a = 3.2 cm, c = 5.6 cm.
b) p = 4.93 cm, β = 70.3°.
c) p = 28 cm, q = 63 cm
d) a = 27.8 cm, A = 373 cm2
e) a : b = 3 : 4, U = 60 cm
2. Wie gross ist in einem Würfel der Winkel zwischen
a) Flächendiagonale und Kante?
b) Raumdiagonale und Kante?
c) Raumdiagonale und Flächendiagonale?
[b = 4.6 cm, β = 55.15°]
[a =14.62, b = 40.84, c = 43.39, α = 19.7°]
[a = 50.48, b = 75.72, c = 91, α = 33.69°]
[b = 26.83, c = 38.64, α = 46.01°]
[a = 15, b = 20, c = 25, α = 36.87°]
[45° oder 90°]
[54.74°]
[35.26°]
3. Berechne die Länge der Strecke f.
Es ist: c=1.7cm; d=2.5cm; e=3.2cm
[Lösung: f = 7.9 cm]
Vertiefungsübungen
4. Bestimme die Breite x eines Kanals, wenn a = 100 m, b = 80 m und c = 33 m lang ist.
[Lösung: x = 41 m]
5. Über einen Kanal führt eine Brücke wie
in der Skizze rechts dargestellt. Berechne
aus der Brückenlänge und aus den
beiden Neigungswinkeln die grösste Tiefe
d des Kanals.
[d = 26.67 m]
6. Befördert man eineinhalb Kubikmeter Sand über ein feststehendes Förderband, so entsteht
nach dem Abfallen ein kegelförmiger Sandhaufen von 85 cm Höhe. Berechne den
Böschungswinkel dieses Schüttkegels! (Der Böschungswinkel ist der Winkel zwischen einer
Mantellinie und der Grundfläche.)
[33.2 °]
7. Bestimmung der unzugänglichen Strecke AB
werden folgende Messungen durchgeführt:
a = 47 m, b = 12 m und d = 8 m. Bestimme c!
[Lösung: c = 31.33 m]
8. Berechne den Flächeninhalt des Kreissegmentes:
s = 34 cm, α = 17°.
[A = 28.76 cm2]
9. Berechne den Inhalt der bemalten Fläche:
a)
b)
[a) 16.82 E2; b) 43.72 E2]
10. Zeichne in einem Halbkreis mit r=5 cm das einbeschriebene Quadrat und in diesem den
Inkreis. Berechne die Länge der Sehne MA.
[MA = 4 cm]