Leseprobe - STARK Verlag
Werbung

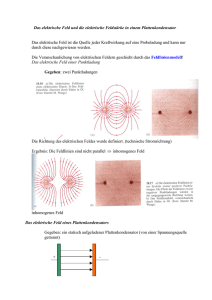
Abitur Physik (Bayern) 2016 Themenbereich I: Elektromagnetische Felder, Relativitätstheorie Aufgabenvorschlag 1 1. Modell der Zündanlage eines Autos Bei einem Ottomotor wird die Verbrennung des Benzin-Luft-Gemisches durch den Funken einer Zündkerze ausgelöst. In Abb. 1 ist das elektrische Feldlinienbild zwischen den geladenen Elektroden der Zündkerze unvollständig eingezeichnet. Abb. 1 a) Ergänzen Sie in Abb. 1 die Feldlinienrichtung und die elektrischen Feldlinien durch die Punkte A, B und C. b) Erklären Sie mithilfe der Abb. 1, dass das Potenzial in den Punkten P1 und Q1 bzw. P2 und Q2 bzw. P3 und Q3 jeweils den gleichen Wert besitzt. Zeichnen Sie in Abb. 1 die Äquipotenziallinien durch diese Punkte ein. (4 BE) (6 BE) Der homogene Feldbereich in Abb. 1, in dem die Feldlinien am dichtesten verlaufen, entspricht näherungsweise dem Feld eines luftgefüllten Plattenkondensators mit Plattenabstand 1,2 mm und Plattenfläche 3,0 mm2. Besitzt die elektrische Feldstärke in diesem Feldbereich mindestens den kV , so schlägt ein Funke zwischen den Elektroden über. Wert 12 mm c) Die Kapazität CZK der Zündkerze stimmt näherungsweise mit der Kapazität des angesprochenen Plattenkondensators überein. Zeigen Sie, dass CZK ca. 2,2 ⋅ 10 –14 F beträgt und dass ein Funke zwischen den Elektroden entsteht, wenn an diesen als sogenannte Zündspannung UZ = 15 kV anliegen. 2016-1 (6 BE) Abb. 2 zeigt eine elektrische Beschaltung obiger Zündkerze. Hierbei handelt es sich um ein Modell wesentlicher Elemente der Zündanlage eines Autos. Der Kondensator mit der Kapazität C bleibt Abb. 2 zunächst unberücksichtigt. d) Berechnen Sie die magnetische Feldenergie, die bei geschlossenem Schalter S in der Primärspule des Transformators gespeichert ist, wenn diese die Induktivität 3,0 mH besitzt und durch sie ein Strom der Stärke 10 A fließt. [zur Kontrolle: 0,15 J] e) Der Schalter S wird geöffnet. Beschreiben Sie die ablaufenden physikalischen Vorgänge, die zum Erreichen einer Spannung im KilovoltBereich an der Zündkerze führen, obwohl die Batteriespannung nur 12 V beträgt. Unmittelbar nach dem Öffnen von S besitzt der Kondensator der Kapazität C die Zündspannung UZ = 15 kV sowie die elektrische Feldenergie 18 mJ. Mit dem Funkenüberschlag an der Zündkerze wird ein Großteil dieser Energie zwischen den Elektroden auf der Funkenstrecke freigesetzt. f) Zeigen Sie, dass die Kapazität C deutlich größer als die Kapazität CZK ist. Im Anschluss wird auf der Funkenstrecke magnetische Feldenergie der Sekundärspule freigesetzt und das Benzin-Luft-Gemisch entflammt. Gehen Sie davon aus, dass in dieser sogenannten Glimmphase die Spannung UZK an den Zündkerzenelektroden konstant ist (verAbb. 3 gleiche Diagramm), während die Stärke des Stroms, der durch die leitfähige Funkenstrecke fließt, von 80 mA auf 4,0 mA linear abnimmt. Entnehmen Sie weitere für Rechnungen notwendige Werte dem Diagramm. 2016-2 (2 BE) (6 BE) (3 BE) g) Berechnen Sie, um welchen Faktor sich der Widerstand der Funkenstrecke während der Glimmphase ändert. h) Berechnen Sie die an der Funkenstrecke in der Glimmphase verrichtete elektrische Arbeit und geben Sie diese als Anteil der ursprünglich in der Primärspule gespeicherten Energie an. i) Am Ende der Glimmphase entsteht eine elektromagnetische Schwingung. Stellen Sie qualitativ in einem Diagramm den zeitlichen Verlauf der elektrischen und magnetischen Feldenergie ab Schwingungsbeginn für eine Periodendauer dar. Nehmen Sie an, dass die Feldenergien zu Schwingungsbeginn gleich groß sind, und vernachlässigen Sie die Dämpfung. 2. Untersuchung der Strahlung eines Presenters (Fernbedienung) Ein Presenter strahlt auf Knopfdruck infrarotes Licht der Wellenlänge λIR ab und enthält außerdem einen Laserpointer, der Licht der Wellenlänge λL = 620 nm emittiert. Beide Strahlungen treffen auf ein Gitter mit 800 Strichen pro cm. Zunächst wird die Wand eines Physiksaals in der Entfernung a vom Gitter als Schirm genutzt. Mit dL bzw. dIR wird der Abstand eines Maximums 1. Ordnung vom Maximum 0. Ordnung für die jeweilige Strahlung bezeichnet. a) Zeigen Sie, dass näherungsweise die Beziehung dL ⋅ λIR = dIR ⋅ λL gilt. b) Bestimmen Sie ein sinnvolles Wertepaar für die Größen a und dL, das bei der experimentellen Bestätigung von λL auftreten könnte. c) Statt der Wand als Schirm wird nun eine Digitalkamera verwendet, die auch infrarotes Licht sichtbar macht und nahe hinter dem Gitter positioniert wird. Bestimmen Sie die WellenAbb. 4 länge λIR durch Auswertung des nebenstehenden Kamerabilds. Gehen Sie davon aus, dass die Beziehung aus Teilaufgabe 2 a weiterhin gilt. (4 BE) (6 BE) (7 BE) (7 BE) (4 BE) (5 BE) (60 BE) 2016-3 Tipps und Hinweise zum Aufgabenvorschlag 1 Tipps zu Teilaufgabe 1 r a: Feldlinien und Äquipotenziallinien stehen immer senkrecht aufeinander. r b: Das elektrische Feld ist homogen. Was folgt daraus für die Ortsabhängigkeit des elektrischen Potenzials? r c: Setzen Sie die angegebenen Daten in die Formel für die Kapazität des Plattenkondensators ein. Bestimmen Sie die Feldstärke im vorliegenden Fall und vergleichen Sie mit der angegebenen Durchschlagsfeldstärke. r d: Setzen Sie in die Formel für die magnetische Feldenergie ein. r e: Die Spannungserhöhung findet in zwei Schritten statt: Verwenden Sie das Induktionsgesetz und das Transformatorgesetz in Ihrer Argumentation. r f: Berechnen Sie mithilfe der Formel für die elektrische Feldenergie die Kapazität und vergleichen Sie mit dem Wert aus Teilaufgabe 1 c. r g: Wenden Sie das Ohm’sche Gesetz unter den angegebenen Bedingungen an. r h: Beachten Sie, dass die Stromstärke linear mit der Zeit abnimmt und dass die Spannung konstant ist; die Dauer der Glimmphase lesen Sie aus dem Diagramm ab. Vergessen Sie nicht, das Ergebnis auch als prozentualen Anteil der Ausgangsenergie (Teilaufgabe 1 d) anzugeben. r i: Beachten Sie die Bedingung, dass die beiden Anfangsenergien gleich groß sind. Überlegen Sie, wie viele Maxima und Minima jede der Energieformen in einer Schwingungsperiode durchlaufen (denken Sie dabei an den klassischen Schwingkreis). Tipps zu Teilaufgabe 2 r a: Sie benötigen die beiden Beugungsbedingungen für konstruktive Interferenz und eine geeignete Näherung. r b: Für den Schirmabstand a finden Sie unter Beachtung des Aufgabentextes sicherlich einen sinnvollen, praxisnahen Beispielwert. Den zugehörigen Wert für den Abstand dL berechnen Sie mithilfe Ihrer Überlegungen zu Teilaufgabe 2 a. r c: Ausgangspunkt ist wiederum die in Teilaufgabe 2 a gefundene Beziehung. Bestimmen Sie damit das Verhältnis der Abstände dIR und dL und daraus die gesuchte Wellenlänge. 2016-4 Lösungen zum Aufgabenvorschlag 1 1. a) Feldlinienbild Abb. 5: Feldlinien (Teilaufgabe 1 a) und Äquipotenziallinien (Teilaufgabe 1 b) r r Denken Sie daran: Die Feldlinien stehen senkrecht auf den Elektrodenoberflächen und zeigen vom Pluspol zum Minuspol. b) In den Bereichen der Punkte P1, P2, P3 bzw. Q1, Q2 und Q3 herrscht ein nahezu homogenes elektrisches Feld, die Punkte teilen die jeweilige Feldlinie in vier gleich lange Teilstrecken. Weil sich das Potenzial im homogenen elektrischen Feld linear mit dem Plattenabstand ändert, liegen P1 und Q1 auf der gleichen Äquipotenziallinien, ebenso auch P2 und Q2 sowie P3 und Q3. Äquipotenziallinienbild: siehe Abb. 5. r r r r Erinnern Sie sich an die Formel U = E ⋅ d im Plattenkondensator: U ist die Spannung bzw. Potenzialdifferenz zwischen den Platten, E die elektrische Feldstärke im Feld zwischen den Platten und d der Plattenabstand. Wegen E = konst. im homogenen Feld gilt U ~ d. c) Für die Kapazität des (näherungsweise Platten-)Kondensators ergibt sich mit den genannten Daten (εr, Luft = 1): C ZK = ε 0 ⋅ A As 3,0 ⋅ (10 −3 m) 2 = 8,85 ⋅ 10 −12 ⋅ = 2,2 ⋅ 10 −14 F d Vm 1,2 ⋅ 10 −3 m Bei einer Zündspannung von UZ = 15 kV entsteht ein Funke, weil die damit kV übertrifft: verbundene elektrische Feldstärke den Grenzwert E grenz = 12 mm E= UZ 15 ⋅ 10 3 V V kV = = 1,25 ⋅ 10 7 = 12,5 > E grenz d m mm 1,2 ⋅ 10 −3 m d) Die (maximale) magnetische Feldenergie ist 1 1 E mag, primär = L ⋅ I 2 = ⋅ 3,0 ⋅ 10 −3 H ⋅ (10 A) 2 = 0,15 J. 2 2 2016-5