1. Übung - FH Dortmund
Werbung

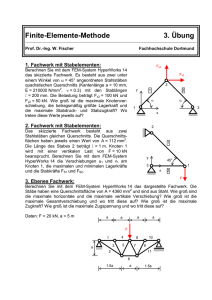
Finite-Elemente-Methode 1. Übung ____________________________________________________________________________________________________________ Prof. Dr.-Ing. W. Fischer Fachhochschule Dortmund 1. Zwei in Reihe geschaltete Federelemente: Berechnen Sie mit dem FEM-System HyperWorks 14 das dargestellte Federsystem, bestehend aus zwei in Reihe geschalteten Federn mit den Federsteifigkeiten c1 = 2 N/mm und c2 = 5 N/mm und den Federlängen l1 = 100 mm und l2 = 100 mm, wenn dieses mit den Druckkräften F1 = 30 N und F2 = 20 N belastet wird. Wie groß ist die größte Knotenverschiebung und wo tritt diese auf? F1 c1 F2 c2 Lösung: umax = 25 mm bei F1 2. Federsystem aus vier Federelementen: Vier Federn mit den Federkonstanten c1 = 200 N/cm, c2 = 400 N/cm, c3 = 500 N/cm und c4 = 600 N/cm sind mit ihren Enden in der Mitte miteinander verbunden. Ihre anderen Enden sind in den Ecken eines Quadrates mit der Seitenlänge a = 100 mm gelenkig befestigt. Der Mittelpunkt des Federsystems wird mit einer Horizontalkraft F = 2 kN belastet. Wie groß sind die Verschiebungen des Mittelpunktes? c2 c1 F c3 100 c4 100 Lösung: uM = 24.3 mm, vM = 4.29 mm, wM = 0 mm fM = 24.7 mm Finite-Elemente-Methode Lösungen zur 1. Übung von Prof. Dr.-Ing. Wilfried Fischer, Fachhochschule Dortmund, 7. Auflage, Wintersemester 2016/17 1. Zwei in Reihe geschaltete Federelemente: Berechnen Sie mit dem FEM-System HyperWorks 14 das dargestellte Federsystem, bestehend aus zwei in Reihe geschalteten Federn mit den Federsteifigkeiten c1 = 2 N/mm und c2 = 5 N/mm und den Federlängen l1 = 100 mm und l2 = 100 mm, wenn dieses mit den Druckkräften F1 = 30 N und F2 = 20 N belastet wird. Wie groß ist die größte Knotenverschiebung und wo tritt diese auf? F1 c1 F2 c2 Lösung: umax = 25 mm bei F1 Lösungsweg mit HyperWorks 14.0 (HyperMesh und OptiStruct): Das Federsystem wird mit drei Knoten (Nodes) und zwei Federelementen (CBUSH) modelliert. Berechnet werden die Verschiebungen (displacements) der Knoten. Einzugebende Daten sind fett und kursiv, Fenster-, Felder- und Boxenbezeichnungen sind nur kursiv und anzuklickende Felder sind nur fett gedruckt. Da HyperWorks (wie fast alle kommerziellen FEM-Systeme) ohne Einheiten arbeitet, muss darauf geachtet werden, dass alle verwendeten Einheiten zueinander passen. Es werden stets nur Zahlenwerte von physikalischen Größen eingegeben. Im Text werden die zugehörigen Einheiten in eckigen Klammern [...] angegeben. Für dieses Beispiel werden als Einheiten [mm] für Längenabmessungen und [N] für Kraftangaben gewählt. - Programmstart: Start / Programme / Altair HyperWorks 14.0 / HyperMesh 14.0 - Voreinstellung: User Profiles: OptiStruct OK - 3 Knoten: Mesh / Create / Nodes: x = 0.000 [mm] y = 0.000 [mm] z = 0.000 [mm] create x = 100.000 [mm] y = 0.000 [mm] z = 0.000 [mm] create x = 200.000 [mm] y = 0.000 [mm] z = 0.000 [mm] create return - Modell zentrieren: Runder Icon links oben: Fit Model -6- Finite-Elemente-Methode Lösungen zur 1. Übung von Prof. Dr.-Ing. Wilfried Fischer, Fachhochschule Dortmund, 7. Auflage, Wintersemester 2016/17 - 2 Eigenschaften: Properties / Create / Properties: Properties / Create / Properties: Name: Feder 1 Card Image: PBUSH Changing …: Ja K_LINE: K1: 2.000 [N/mm] Close Name: Feder 2 Card Image: PBUSH Changing …: Ja K_LINE: K1: 5.000 [N/mm] Close - 2 Federelemente: Mesh / Create / 1D Elements / Springs: create elem types = CBUSH property = Feder 1 1. Knoten anklicken 2. Knoten anklicken property = Feder 2 2. Knoten anklicken 3. Knoten anklicken return - Lager- u. Lastfälle: Collectors / Create / Load Collectors: Collectors / Create / Load Collectors: - 2 Einzelkräfte: BCs / Create / Forces: - Lager aktivieren: Roter Icon rechts unten: -7- Name: Lager Color: Card Image: <None> Close Name: Last Color: Card Image: <None> Close create nodes global system magnitude = 30.000[N] x-axis magnitude % = 50.000 label loads load types = FORCE 1. Knoten anklicken create magnitude = 20.000[N] 2. Knoten anklicken create return Set Current Load Collector Finite-Elemente-Methode Lösungen zur 1. Übung von Prof. Dr.-Ing. Wilfried Fischer, Fachhochschule Dortmund, 7. Auflage, Wintersemester 2016/17 - Einspannung: BCs / Create / Constraints: create nodes size = 10.000 label constraints constant value dof1 = 0.000 [mm] dof2 = 0.000 [mm] dof3 = 0.000 [mm] dof4 = 0.000 dof5 = 0.000 dof6 = 0.000 load types = SPC 3. Knoten anklicken create return - Modell zentrieren: Runder Icon links oben: Fit Model - Rechenschritte: Setup / Create / LoadSteps: Name: Statik Analysis type: Linear Static SPC: Loadcol Lager 1 OK LOAD: Loadcol Last 2 OK Close - Speicherung: File / Save As: U011 Speichern - Berechnung: Applications / OptiStruct: input file: ...U011.fem export options: all run options: analysis memory opt.: default options: -optskip OptiStruct - FEM-Analyse: ANALYSIS COMPLETED.: Close -8- Finite-Elemente-Methode Lösungen zur 1. Übung von Prof. Dr.-Ing. Wilfried Fischer, Fachhochschule Dortmund, 7. Auflage, Wintersemester 2016/17 - Verschiebungen: Post / Deformed: simulation = SUB1 – Statik data type = Displacements model units = 10.000 as selected as selected deform - Verschiebungen: Post / Contour: - Programm Ende: File / Exit: simulation = SUB1 – Statik data type = Displacements params x comp model units = 10.000 mult = 1.000 min/max titles contour umax = 25 mm -9- Finite-Elemente-Methode Lösungen zur 1. Übung von Prof. Dr.-Ing. Wilfried Fischer, Fachhochschule Dortmund, 7. Auflage, Wintersemester 2016/17 Falls schon Daten vorliegen, muss zunächst das FEM-Modell geladen werden. Anschließend müssen die dazugehörigen Ergebnisse geladen werden: - Programmstart: Start / Programme / Altair HyperWorks 14.0 / HyperMesh 14.0 - Voreinstellung: User Profiles: OptiStruct OK - FEM-Modell: File / Open: U011.hm Öffnen - FEM-Ergebnisse: File / Load / Results: U011.res Öffnen - Verschiebungen: Post / Deformed: simulation = SUB1 – Statik data type = Displacements model units = 10.000 as selected as selected deform - Verschiebungen: Post / Contour: - Programm Ende: File / Exit: simulation = SUB1 – Statik data type = Displacements params x comp model units = 10.000 mult = 1.000 min/max titles contour umax = 25 mm - 10 - Finite-Elemente-Methode Lösungen zur 1. Übung von Prof. Dr.-Ing. Wilfried Fischer, Fachhochschule Dortmund, 7. Auflage, Wintersemester 2016/17 2. Federsystem aus vier Federelementen: Vier Federn mit den Federkonstanten c1 = 200 N/cm, c2 = 400 N/cm, c3 = 500 N/cm und c4 = 600 N/cm sind mit ihren Enden in der Mitte miteinander verbunden. Ihre anderen Enden sind in den Ecken eines Quadrates mit der Seitenlänge a = 100 mm gelenkig befestigt. Der Mittelpunkt des Federsystems wird mit einer Horizontalkraft F = 2 kN belastet. Wie groß sind die Verschiebungen des Mittelpunktes? c2 c1 F c3 100 c4 100 Lösung: uM = 24.3 mm, vM = 4.29 mm, wM = 0 mm - 11 - fM = 24.7 mm