Magentisches Feld
Werbung
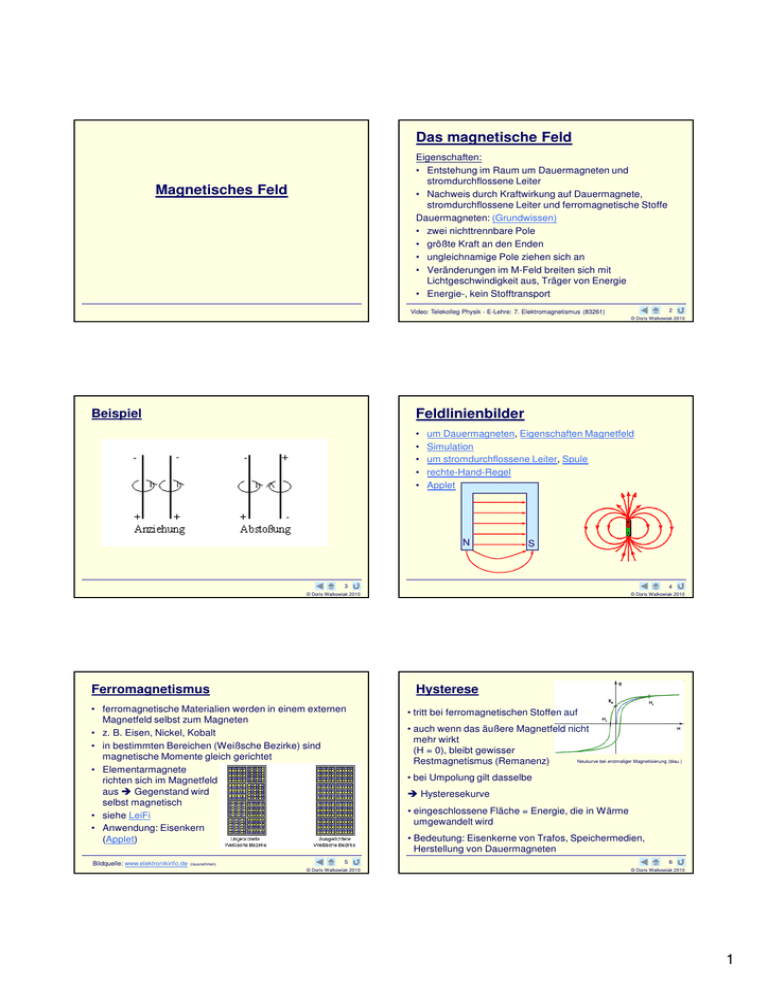
Das magnetische Feld Eigenschaften: • Entstehung im Raum um Dauermagneten und stromdurchflossene Leiter • Nachweis durch Kraftwirkung auf Dauermagnete, stromdurchflossene Leiter und ferromagnetische Stoffe Dauermagneten: (Grundwissen) • zwei nichttrennbare Pole • größte Kraft an den Enden • ungleichnamige Pole ziehen sich an • Veränderungen im M-Feld breiten sich mit Lichtgeschwindigkeit aus, Träger von Energie • Energie-, kein Stofftransport Magnetisches Feld 2 Video: Telekolleg Physik - E-Lehre: 7. Elektromagnetismus (83261) © Doris Walkowiak 2010 Feldlinienbilder Beispiel • • • • • um Dauermagneten, Eigenschaften Magnetfeld Simulation um stromdurchflossene Leiter, Spule rechte-Hand-Regel Applet N S 3 4 © Doris Walkowiak 2010 Ferromagnetismus Hysterese • ferromagnetische Materialien werden in einem externen Magnetfeld selbst zum Magneten • z. B. Eisen, Nickel, Kobalt • in bestimmten Bereichen (Weißsche Bezirke) sind magnetische Momente gleich gerichtet • Elementarmagnete richten sich im Magnetfeld aus Gegenstand wird selbst magnetisch • siehe LeiFi • Anwendung: Eisenkern (Applet) Bildquelle: www.elektronikinfo.de (rausnehmen) © Doris Walkowiak 2010 5 © Doris Walkowiak 2010 • tritt bei ferromagnetischen Stoffen auf • auch wenn das äußere Magnetfeld nicht mehr wirkt (H = 0), bleibt gewisser Neukurve bei erstmaliger Magnetisierung (blau ) Restmagnetismus (Remanenz) • bei Umpolung gilt dasselbe Hysteresekurve • eingeschlossene Fläche = Energie, die in Wärme umgewandelt wird • Bedeutung: Eisenkerne von Trafos, Speichermedien, Herstellung von Dauermagneten 6 © Doris Walkowiak 2010 1 Magnetische Flussdichte Beispiele/Aufgabe Ziel: • Berechnung der Kraft auf einen stromdurchflossenen Leiter im M-Feld • Experiment: Applet Magnetfeld der Erde in Deutschland F~I F F = konst. ⇒ =B F ~ I ⋅ l ⇒ F~l I⋅l I⋅l Flussdichte in 1 cm Entfernung vom Pol eines keramischen Magneten 0,005 T Flussdichte in der Plasmakammer einer Anlage zur Kernfusion 2T Wie groß muss die magnetische Flussdichte sein, damit ein 15 cm langer Leiter bei einem Strom von 5 A eine Kraftwirkung von 0,15 N erfährt? (0,2 T) • Die magnetische Flussdichte gibt an, wie stark ein magnetisches Feld ist F • FZ: B Einheit: T (Tesla) Gleichung: B = I⋅l • Bedingungen: homogenes r r r M-Feld, r gerader Leiter, F ⊥ B I ⊥ B Video: TK Physik - E-Lehre: Kraft auf bewegte Ladung (83262) nur 1. Teil 0,00002 T 7 8 © Doris Walkowiak 2010 © Doris Walkowiak 2010 Magnetische Flussdichte einer Spule Aufgabe Voraussetzung: • l >> d (lange Spule • Wie groß ist die magnetische Flussdichte einer 20 cm langen Spule mit 1000 Windungen, wenn ein Strom von 1A fließt? • Wie verändert sich die Flussdichte, wenn ein Eisenkern (µrel = 500) verwendet wird? im Inneren homogenes Feld) B~I N N N B ~ I ⋅ ⇒ B = µ 0 ⋅ ⋅ I l l B~ l im Vakuum (annähernd auch in Luft) N ⋅I l Vs 1000 B = 1,256 ⋅ 10 −6 ⋅ ⋅ 1A Am 0,2m B = µ 0 ⋅ µ rel ⋅ µ0 … magnetische Feldkonstante µ0 = 1,256 · 10-6 Vs/Am • allgemein: B = µ 0 ⋅ µ rel ⋅ N ⋅I l µrel … relative Permeabilität (berücksichtigt vor allem den Einfluss ferromagnetischer Stoffe) Video: TK Physik - E-Lehre: Kraft auf bewegte Ladung (83262) 2. Teil B = 6,28 ⋅ 10 −3 T mit Eisenkern: B = 3,14 T 9 10 © Doris Walkowiak 2010 © Doris Walkowiak 2010 Magnetische Feldstärke Lorentzkraft • erfasst nur den Einfluss der Feld erzeugenden Teile einer Spule, nicht die verstärkende Wirkung durch den Stoff N • FZ: H Einheit: A/m Gleichung: H = I⋅ • Kraftwirkung auf bewegte Ladungsträger im M-Feld l für lange Spule (l>>d) B = µ 0 ⋅ µ rel ⋅ H F = B · l · I (Kraft auf geraden Leiter, Q e I= = e...Elementarladung t t e ⇒ F = B⋅l⋅ t l v = ⇒ F = B⋅v⋅e t FL = e ⋅ v ⋅ B FL ...Lorentzkraft r r ( v ⊥ B) r r r r F⊥B I ⊥B ) • wirkt immer senkrecht zur Bewegungsrichtung 11 © Doris Walkowiak 2010 http://www.schule-bw.de/unterricht/faecher/physik/online_material/e_lehre_2/teilchenfeld/e_bfeld.htm 12 © Doris Walkowiak 2010 2 Aufgabe Drei-Finger-Regel • Foto • Applet • Applet • Welche Kraft wirkt auf ein Elektron, welches mit einer Geschwindigkeit von 3*107 m/s in ein Magnetfeld der Stärke 0,1 T eingeschossen wird? FL = e ⋅ v ⋅ B = FL = 1,602 ⋅ 10 −19 C ⋅ 3 ⋅ 10 7 m ⋅ 0,1T s • LeiFi FL = 4,8 ⋅ 10 −13 N 13 © Doris Walkowiak 2010 Spezifische Ladung eines Elektrons 14 Bildquelle: http://www.brunnermeiers.de/kasim/hand.htm © Doris Walkowiak 2010 Spezifische Ladung eines Elektrons • Experiment • Animation E kin = E el m 2 v = e⋅U 2 ⇒ v2 = FL = FRad m ⋅ v2 r e⋅B⋅r ⇒v= m ⇒ e⋅v⋅B = 2e ⋅ U m e⋅B⋅r v2 = m 2 2e ⋅ U e 2 ⋅ B 2 ⋅ r 2 = m m2 e 2U ⇒ = m r 2 ⋅ B2 ⇒ Messung von U, B, r e/m = 1,76 × 1011 As/kg ... spezifische Elektronenladung Möglichkeit, die Masse eines Elektrons zu bestimmen (Ladung e wurde mit Millikan ermittelt) Video: TK Physik - E-Lehre: Kraft auf bewegte Ladung (83262) letzter Teil Hall-Effekt 15 Beispiel: geg.: vD = 1 mm/s B = 1,2 T b = 1 cm U H = b ⋅ v ⋅ B = 0,01m ⋅ 0,001 ges.: UH m ⋅ 1,2T = 12µV s Wovon hängt die Hallspannung außerdem ab? FL = Fel Stromstärke b U ⇒ e⋅v⋅B = e⋅ b ⇒ UH = b ⋅ vD ⋅ B UH = Bild: http://www.schule-bw.de/unterricht/faecher/physik/online_material/e_lehre_2/teilchenfeld/halleffekt.htm I⋅B I⋅B = RH ⋅ N⋅e⋅d d RH … Hallkonstante (TW) RH = V/(N*e) … Maß für Ladungsträgerdichte Anwendung: Hallsonde vD … Driftgeschwindigkeit (in Metallen rund 1 mm/s) S. 286 © Doris Walkowiak 2010 Hall-Effekt (Edwin H. Hall (1855-1938)) • auf bewegte Ladungsträger wirkt in einem äußerem magnetischen Feld eine Kraft Lorentzkraft in einem stromdurchflossenen Leiter kommt es zur Ladungsverschiebung in flächenhaftem Leiter ist eine Spannung messbar (Hallspannung) • Spannung wächst so lange, bis FL = Fel ⇒ e⋅v⋅B = e⋅E 16 © Doris Walkowiak 2010 17 © Doris Walkowiak 2010 Herleitung 18 © Doris Walkowiak 2010 3 Hall-Effekt Geschwindigkeitsfilter (1) • dient dazu, alle elektrisch geladenen Teilchen, die in ihn hineingeschossen werden, herauszufiltern, die nicht die gewünschte Geschwindigkeit besitzen • ermöglicht auch die Bestimmung der Geschwindigkeit von geladenen Teilchen • Plattenkondensator, dessen homogenes elektrisches Feld mit einem senkrecht dazu liegenden homogenen magnetischen Feld überlagert wird. • • Edwin Hall verwendete zum Nachweis des von ihm entdeckten Effekts ein dünnes Goldband. War das Material eine gute Wahl? Ermittle die Driftgeschwindigkeit von Elektronen in Gold für die gleichen Parameter (Stromstärke I = 1 A , Fläche A = 1 mm2). (2) • • • In einem Halbleiterplättchen (b = 5 mm, Dicke d = 1 mm) misst man eine Hallspannung von 100 µV. Die Stärke des Stroms durch das Plättchen beträgt 50 mA und es wirkt ein Magnetfeld der Stärke 0,2 T senkrecht zum Plättchen. Wie groß ist die Driftgeschwindigkeit v der Elektronen im Halbleitermaterial? Wie groß ist die Hallkonstante? Vergleiche Deine Ergebnisse mit den Werten für Kupfer. 19 Lösungen??? FL = Fel e⋅v⋅B = e⋅E v= E B 20 http://www.phynet.de/e-lehre/geschwindigkeitsfilter © Doris Walkowiak 2010 © Doris Walkowiak 2010 Anwendungen Aufgaben • • • • • • • • • 1. Elektronen treten senkrecht zu den Feldlinien in ein homogenes Magnetfeld mit B = 1,2 · 10-3 T ein und werden auf eine Kreisbahn mit einem Radius von 25 mm gezwungen. Berechne die Geschwindigkeit der Elektronen! (Leite die erforderliche Gleichung her und begründe den Ansatz!) - Abi 85/86 v = 5,3×106 m/s 2. Ein Elektronenstrahl tritt mit einer Geschwindigkeit von 4,5×106 m/s senkrecht zu den Feldlinien in ein homogenes Magnetfeld mit b = 1,2 · 10-3 T ein. Begründe, dass eine Kreisbahn entsteht und berechne r = 2,1 cm den Radius! - Abi 81/82 Elektromagnet Relais Klingel Magnetfeld der Erde, Folie Kernspintomograph Motor, Kommutator, Animation, Applet Sonnenwind, Polarlicht Elektronenmikroskop Teilchenbeschleuniger 21 22 © Doris Walkowiak 2010 © Doris Walkowiak 2010 Aufgaben Aufgaben 3. a) Vergleichen Sie elektro- und magnetostatische Felder hinsichtlich ihrer Entstehung, ihres Nachweises und ihrer Beschreibung! b) An einer Fernsehbildröhre liegt zwischen Katode und Anode eine Spannung von 15 kV an. Welche Geschwindigkeit und welche Energie erreichen die Elektronen durch diese Spannung? c) In einer Luftspule mit 800 Windungen, einer Länge von 5 cm und einem Widerstand von 45 W soll ein magnetostatisches Feld mit einer magn. Flussdichte von 12 mT erzeugt werden. Welche Spannung muss angelegt werden? 4. In einem Vakuum werden zwei verschiedene einfach positiv geladene Ionen mit den Massen m1 = 6,47×10-26 kg und m2 = 6,80×10-26 kg mit gleicher Geschwindigkeit v = 5,2×104 m/s senkrecht zu den Feldlinien in ein homogenes M-Feld geschossen und durch dieses auf eine Kreisbahn gelenkt (B = 200 mT). Berechnen Sie das Verhältnis der Bahnradien! Welche Zeiten benötigen die Ionen für einen Umlauf? - Abi 89/90 Ekin = 15 keV v = 7,3×107 m/s r1/r2 = 0,951 T1 = 12,7×10-3 s T2 = 13,3×10-3s 5. Eine Spule hat 1000 Windungen und eine Länge von 12 cm (R = 12,6 W). An die Spule (µrel = 1) wird eine Gleichspannung von 45 V angelegt. Berechne die magnetische Flussdichte im homogenen Teil des MFeldes! B = 0,0375 T U = 26,8 V 23 © Doris Walkowiak 2010 24 © Doris Walkowiak 2010 4 Aufgaben Quellen 6. In der Abbildung wirkt ein homogenes Magnetfeld nur im umrandeten Bereich. Im Punkt A treten Elektronen mit konstantem Geschwindigkeitsbetrag in das M-Feld ein; im Punkt P verlassen sie es wieder a) Wie muss das M-Feld gerichtet sein? b) Zeichnen Sie die Bahnkurve über den Punkt P hinaus weiter (Gravitationskraft einflusslos)! c) Die kinetische Energie eines Elektrons beträgt im Punkt A 1000 eV. Wie groß ist dort seine Bahngeschwindigkeit? • • • • Umkehr Erdmagnetfeld Elektronikinfo Kreuzworträtsel http://www.schulebw.de/unterricht/faecher/physik/online_material/e_lehre_ 2/teilchenfeld/ v = 1,88×107 m/s d) Die magn. Flussdichte wird verdoppelt. Wie verändert sich die Bahnkurve? Begründen Sie! e) Die Eintrittsgeschwindigkeit wird verdoppelt. Wie verändert sich die Bahnkurve? Begründen Sie! 25 26 © Doris Walkowiak 2010 Backup © Doris Walkowiak 2010 Backup: Herleitung Hallspannung • Vergleich Teilchen im E-und M-Feld • Drehung einer Leiterschleife im Magnetfeld Q n⋅e n⋅e⋅v = = t t l I⋅l ⇒v= n ⋅e I= n n = V d⋅b⋅l l 1 I ⇒ = ⇒v= n cL ⋅ d ⋅ b cL ⋅ d ⋅ b ⋅ e Ladungsträgerdichte c L = UH = v ⋅ b ⋅ B = ⇒ UH = R H ⋅ 27 © Doris Walkowiak 2010 I I ⋅b⋅B = ⋅B cL ⋅ d ⋅ b ⋅ e c Ld ⋅ e RH = 1 cL ⋅ e I⋅B d 28 © Doris Walkowiak 2010 Lösungen Hallspannung 1. I = Q = N ⋅ e = N ⋅ e ⋅ v t t l l N⋅e V A ⋅l RH = = N ⋅e N ⋅e ⇒ v = I⋅ ⇒v= RH ⋅ I = A m3 ⋅ 1A m C = −7,2 ⋅ 10 − 5 s 1 ⋅ 10 − 6 m 2 − 7,2 ⋅ 10 −11 2. U = b ⋅ v ⋅ B ⇒ v = U H = H b⋅B 0,1mV m = 0,1 5mm ⋅ 0,2T s I⋅B d 1mm m3 ⇒ RH = ⋅ UH = ⋅ 100 ⋅ 10 − 6 V = 1 ⋅ 10 −5 d I⋅B 50mA ⋅ 0,2T C m3 Kupfer : R H = −5,2 ⋅ 10 −11 C UH = R H ⋅ 29 © Doris Walkowiak 2010 5