Übungsaufgaben zur Vorbereitung auf die Eignungsprüfung an

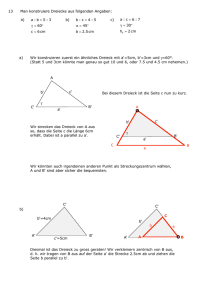
Übungsaufgaben zur Vorbereitung auf die Eignungsprüfung
an Kollegs in Rheinland-Pfalz
1.
Bruchrechnung
x - 3 2x + 5 3x -1
a)
+
=
2
3
6
c) Dividieren Sie die Summe der Zahlen
†
2.
†
3.
†
†
4.
†
5.
†
Rechnen mit binomischen Ausdrücken
a) 7 ⋅ (2x - y ) ⋅ (2x + y ) =
†
2
ˆ
a 2 + b 2 Ê ( a + b)
c)
:Á
-1˜˜ =
a ⋅ b ÁË 2a ⋅ b
¯
b)
Ê 2
ˆ 5
Á1 x + 1,5˜ : =
Ë 3
¯ 3
5
und 0,4 durch ihre Differenz!
7
†
b)
28x 2 - 28xy + 7y 2 =
d)
2x + 1
⋅15 ⋅ (2x -1) =
75 ⋅ ( 4 x 2 -1)
†
Lineare Gleichungen, Bruchgleichungen
10
1
=6
x +1 x - 2
c) Welchen Winkel schließen der große und der kleine Uhrzeiger um 15.05 Uhr ein?
40
d) Welche Zahl muss von Zähler und Nenner des Bruches
subtrahiert und zu Zähler
51
†
8
und Nenner des Bruches
addiert werden, damit zwei gleich große Brüche
13
entstehen?
†
a)
(3x - 5)
2
- (2x + 3) ⋅ ( 3 - 2x ) = 2x ⋅ ( 7x -†
22) - ( x + 6)
Gleichungssysteme, Textaufgaben
†
I 4 x + 7y = 11
a)
II 6x - 5y = -30
2
b)
x
= - + 10
2
II 3y - 2x + 12 =
0
c) Bei einer Stichwahl siegte Kandidat A mit 27 Stimmen Mehrheit gegen Kandidat B;
das Stimmenverhältnis war 4:3 für ihn. Wie viele gültige Stimmen wurden insgesamt
abgegeben, wie viele für A, wie viele für B?
† Griechen gegen die Zentauren. Im Gefecht
d) Nach einer Sage von Homer kämpften die
waren insgesamt 420 Köpfe und 1040 Beine. Wie viele Griechen und wie viele
Zentauren (mit 4 Beinen) waren beteiligt?
e) Isopropylalkohol wird in verdünnter Form für kühlende Umschläge benutzt. Ein
Apotheker will aus 90%igem und 10%igem Isopropylalkohol 300 ml einer 70%igen
Lösung mischen. Wie viel muss er von der 90%igen und wie viel von der 10%igen
Lösung nehmen?
f) Zwei Kapitalien, von denen das eine zu 4%, das andere zu 5% ausgeliehen ist,
bringen jährlich zusammen 3000 € Zinsen. Wäre jedes Kapital um 1% höher
ausgeliehen, so würden die jährlichen Zinsen 660 € mehr betragen. Wie groß sind
beide Kapitalien?
Quadratische Gleichungen
a) x 2 + 3x + 2 = 0
†
b)
I
b)
( x + 8)
y
2
2
- ( x - 8) = x 2 + 24 x + 7
6.
7.
Geometrische Grundkonstruktionen (nur mit Zirkel und Lineal)
a) Konstruieren Sie das Lot auf die Gerade g von einem Punkt P außerhalb der Geraden
g!
b) Errichten Sie die Senkrechte im Punkt P einer gegebenen Geraden g!
c) Zeichnen Sie die Geradenkreuzung (g, h) mit dem Winkel a = 50 0 ! Konstruieren Sie
dann die Winkelhalbierende von a !
d) Spiegeln Sie das DABC mit A(-13), B(2 -1), C (5 2) an der x-Achse eines kart.
Koordinatensystems! Verschieben Sie das gespiegelte
Dreieck so, dass der neue
†
*
*
Eckpunkt A die Koordinaten
A (14 ) erhält!
†
†
Dreieckskonstruktionen, Kongruenzsätze
Konstruieren
Sie ein Dreieck aus hc = 5cm, b = 70 0 , g = 36 0
†
†
C
g
b
†
c
a
A
a
h
c
p
D
b
q
B
8.
Satzgruppe von Pythagoras, Strahlensätze
a) Welche Sätze gelten im rechtwinkligen Dreieck? (rechter Winkel bei C – Skizze
siehe Aufg. 7)
b) Gegeben sei ein Dreieck mit a = 30 cm, b = 40 cm und c = 50 cm. Zeigen Sie, dass
das Dreieck rechtwinklig ist und berechnen Sie die Höhe hc dieses Dreiecks!
c) Teilen Sie eine Strecke s = 10 cm zeichnerisch (ohne Maßstab!) im Verhältnis 3:4!
d) Ein Dia (Höhe 24 mm; Breite 36 mm) soll so an die Wand projiziert werden, dass
das Bild 1,44 m breit wird. Berechnen Sie den Abstand Dia – Wand, wenn sich die
†
Projektionslampe 15 cm hinter dem Dia befindet!
9.
Strecken-, Flächen- und Volumenberechnungen
a) Auf einen Würfel mit der Kantenlänge a wird eine vierseitige Pyramide mit gleicher
Kantenlänge gesetzt. Berechnen Sie das Gesamtvolumen des Körpers!
b) Gegeben ist eine dreiseitige gerade Glassäule, bei der alle Kanten 5 cm lang sind.
Welche Oberfläche hat die Säule?