Klausur 12.1 No. 2

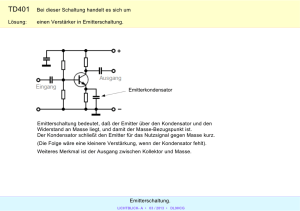
Ph LK 12.1
Klausur Nr. 2
30.11.07
Name:
Zugelassene Hilfsmittel: Taschenrechner, Formelblatt
Aufgabe 1: Kondensatorauf- und entladung
Ein Kondensator soll über einem Widerstand aufbzw. entgeladen werden.
a) Erläutern Sie, warum das Einbringen eines
Dielektrikums die Kapazität eines Kondensators
erhöht. Benutzen Sie Skizzen.
R
C1
U0
b) Im Kondensator (C = 100 µF) ist nach dem Aufladen eine Energie von W = 20 mJ gespeichert.
Bestimmen Sie die Ladung des Kondensators und die Stromstärke am Beginn des Entladungsvorgangs
über einem Widerstand von R = 100 kΩ. Ermitteln Sie die Funktion der Spannung am Kondensator
und die Funktion der Stromstärke während des Entladevorgangs.
c) Für die Aufladekurve soll jetzt die Differentialgleichung aufgestellt werden.
Erläutern Sie den Ansatz U 0 = U R (t ) + U C (t ) und zeigen Sie, dass sich daraus folgende DGL ergibt:
Q(t ) Q0
Q& (t ) +
−
=0
RC RC
d) Zeigen Sie, dass die folgende Funktion eine Lösungsfunktion dieser DGL ist:
Q(t ) = Q0 − Q0 exp(− kt ) .
Ermitteln Sie daraus allgemein die Abhängigkeit der Konstante k von R und C.
e) Erläutern Sie den Begriff der Halbwertszeit und leiten Sie die Beziehung τ = RC ⋅ ln(2) aus der
 t 
 her.
 RC 
Aufladefunktion Q (t ) = Q0 − Q0 ⋅ exp −
Wir verändern nun unsere Schaltung, wie in der Skizze dargestellt um einen weiteren Kondensator C2,
der baugleich zum ersten ist.
U0 = 9 V
R
R = 100 kΩ
+
U0
+
C1 = C2 = 100µF
C1
+
C2
V
Der erste Kondensator wird durch die Quelle aufgeladen. Nach Umlegen des Schalters wird am
zweiten Kondensator die im Anhang befindliche Spannungskurve aufgenommen. Wir wollen nun
theoretische Überlegungen und experimentelle Befunde miteinander verbinden.
f) Begründen Sie die hier auftretende maximale Aufladespannung von 4,5 V.
--- Seite 1/2 ---
Ph LK 12.1
Klausur Nr. 2
30.11.07
Name:
Zugelassene Hilfsmittel: Taschenrechner, Formelblatt
g) Berechnen Sie theoretisch, die sich für diese Aufladung ergebene Halbwertszeit (Tipp: Ein grobes
Ablesen des Wertes aus dem Diagramm kann helfen!). Begründen Sie Ihre Berechnung.
h) Wählen Sie aus der Messkurve vier geeignete Punkte und bestimmen Sie mit Hilfe des Ansatzes
U C (t ) = U 0 (1 − exp(− kt )) die Konstante k graphisch. Berechnen Sie daraus die Halbwertszeit des
Aufladevorgangs.
i)* Erläutern Sie den zeitlichen Verlauf der Spannung und der Stromstärke am zweiten Kondensator,
wenn der Umschalter ein zweites Mal (bzw. mehrfach hintereinander) hin- und zurückbewegt wird.
Aufgabe 2: Coulomb-Feld
+
a) Eine der wichtigsten Anwendungen des Coulomb´schen-Gesetzes behandelt das Atom. Der Abstand
zwischen Proton und Elektron im Wasserstoffatom sei d = 1 ⋅ 10 −10 m . Das Proton trägt die Ladung
q = 1,6 ⋅ 10 −19 C , das Elektron eine gleich große negative. Berechnen Sie die Coulomb-Kraft, mit der
sich die beiden Teilchen anziehen. Wie ändert sich die Kraft, wenn der Abstand der Teilchen
verdoppelt würde? Argumentieren Sie mit Proportionalitäten.
b) Skizzieren Sie das elektrische Feld eines positiv geladenen Atomkerns und erläutern Sie am
Beispiel der Überführungsarbeit, die an einem Elektron geleistet wird, den Begriff Potential. Erläutern
Sie zudem den Begriff der Äquipotentialfläche.
c)
Zwei gleiche Kügelchen (m = 0,50 g) sind jeweils an einem 1,0 m
langen, oben am selben Punkt befestigten Faden aufgehängt. Beide
tragen eine Ladung von ca. 60 nC. Berechnen Sie den sich
zwischen den Kugelmittelpunkten einstellenden Abstand. Der
Ansatz Ihrer Rechnung muss in einem Diagramm deutlich werden.
l
-
Viel Erfolg!
--- Seite 2/2 ---