Q12 * Astrophysik * Aufgaben zur Sternentwicklung
Werbung

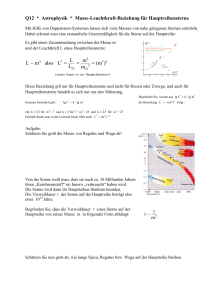
Q12 * Astrophysik * Aufgaben zur Sternentwicklung Aufgaben zum Hauptreihenstadium 1 . m2 2. Zeigen Sie, dass aus L* ≤ 105 für die Masse m eines Sterns m 50 m folgt. 1. Begründen Sie, dass für die Verweildauer τ auf der Hauptreihe gilt: 3. Schätzen Sie für sehr massereiche Hauptreihensterne ( B0 mit M ≈ – 5) die Masse und die Verweildauer auf der Hauptreihe ab. Lösungen 1 , denn m2 1. Für die Verweildauer τ auf der Hauptreihe gilt m , denn die Verweildauer ist proportional zur Masse des Brennstoffvorrats. 1 , denn je größer L umso größer der Brennstoffverbrauch. L m m 1 Wegen L m3 für Hauptreihensterne folgt damit 2 3 L m m 2. Aus L* ≤ 105 folgt m 50 m , denn L L m3 m L mm L m 3 3 * 3 L m L 3 L* m 3 105 46 m 50 m 3. Für einen Hauptreihenstern B0 mit M ≈ – 5 gilt: M M 2,5 lg L L L* m* m* 3 3 L* L* 3 L 10 0,4 (M L 8,3 104 44 M) 10 0,4 (4,8 5) 10 3,92 8,3 10 4 also m 44 m m 2 1 1 10 109 a 9 und 10 a 2 2 2 5 Millionen Jahre m2 m 44 44 442 Aufgaben zu Roten Riesen 1. Erklären Sie den Namen „Drei-Alpha-Prozess“ für die folgende Fusionsreaktion! He 4 + He 4 → Be 8 + γ – 0,09 MeV und Be 8 + He 4 → C 12 + γ + 7 MeV Lösung: Es müssen hier (nahezu gleichzeitig) drei Heliumkerne zusammenstoßen. Eine Gesamtgleichung lautet He4 + He 4 + He 4 → C 12 + γ + γ + 7 MeV 2. Beteigeuze im Sternbild Orion ist ein Pulsationsveränderlicher und etwa 600 Lj entfernt. Der Winkeldurchmesser des Sterns schwankt etwa zwischen 0,026´´ und 0,042´´ mit einer halbregelmäßigen Periode von ca. 2000 Tagen, die scheinbare Helligkeit nimmt Werte zwischen 0,3 und 0,6 an. Die Oberflächentemperatur beträgt etwa 3500K. a) Berechnen Sie den maximalen und den minimalen Sternradius von Beteigeuze in Vielfachen der Astronomischen Einheit. b) Welche relative maximale bzw. minimale Leuchtkraft L* hat Beteigeuze? c) Für die Masse von Beteigeuze findet man 20 Sonnenmassen angegeben. Warum stimmt dieser Wert nicht überein mit dem Wert, der sich aus der Masse-Leuchtkraft-Beziehung ergibt? Lösung: a) d 600 Lj 600 9, 46 1011 m 2 R1 d tan 1 1 0, 026o R1 3, 79 107 AE tan ( ) 2, 4 AE d 2 2 3600 tan 1 R2 d tan 2 1 0, 042o 3, 79 107 AE tan ( ) 3,9 AE 2 2 3600 b) L 4R 2 T 4 L1* L2* 600 9, 46 1015 m AE 3, 79 107 AE ( 184 pc) 11 1, 496 10 m L1 R12 T14 (2, 4 1,5 1011 m) 2 (3500 K) 4 2 8,9 103 L R T 4 (1,39 109 m) 2 (5800K) 4 L2 R 2 2 T2 4 (3,9 1,5 1011 m) 2 (3500 K)4 2 23 103 4 9 2 4 L R T (1,39 10 m) (5800K) c) Die Masse-Leuchtkraftbeziehung gilt nur für Hauptreihensterne und nicht für Rote Riesen. Aufgabe zu Neutronensternen a) Welche Dichte hat ein Proton mit der Masse 1,7 ∙ 10-27 kg und dem Radius 1,4 ∙ 10-15 m ? b) Welchen Radius hätte die Sonne, wenn man sie auf die Dichte eines Neutronensterns mit ca. 108 t/cm3 komprimieren könnte? c) Eine rotierende Kugel der Masse M soll pro Sekunde 100 Umdrehungen ausführen. Welche Dichte muss die Kugel mindestens aufweisen, damit sie durch die Gravitationskraft zusammengehalten werden kann? Lösung: m m 1, 7 10 27 kg kg g 1,5 1017 3 1,5 1014 V 4 r 3 4 (1, 4 1015 m)3 m cm3 3 3 m m t g 4 m b) m 2, 0 10 30 kg und 108 1014 r3 3 3 V 4 r3 cm cm 3 3 a) Dichte Pr oton r 3 3 m 4 3 3 2, 0 1030 kg 1, 68...106 cm 17 km 11 3 410 kg / cm c) Für ein Massestück an der Oberfläche muss die Gravitationsanziehung größer sein als die benötigte Zentripetalkraft. 4 2 2 GM 2 m M 2 G M 3 G 4 m 2 r m r G 2 3 4 3 r r 3 T T r 3 4 4 2 3 3 3 kg 2 G 2 1, 4 107 3 3 2 m 3 T 4G T G m T (0, 01s) 2 6, 67 1011 2 kg s 2 Aufgabe Stellare Schwarze Löcher Der Schwarzschildradius R S 2G M gibt an, innerhalb welchen Abstands ein Photon eine Masse c2 M nicht mehr verlassen kann. Bestimmen Sie für die Masse unserer Sonne den Schwarzschildradius! m3 2 6, 67 10 2, 0 10 30 kg 2 2G M kg s 3, 0 103 m 3, 0 km 2 8 2 c (3, 0 10 m / s) 11 Lösung: R S,